2020-2021学年八年级数学人教版下册 18.2.1 矩形的性质课件(21张)
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册 18.2.1 矩形的性质课件(21张) |  | |
| 格式 | ppt | ||
| 文件大小 | 615.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-10 14:29:46 | ||
图片预览




文档简介
18.2 特殊的平行四边形
18.2.1 矩形
第1课时 矩形的性质
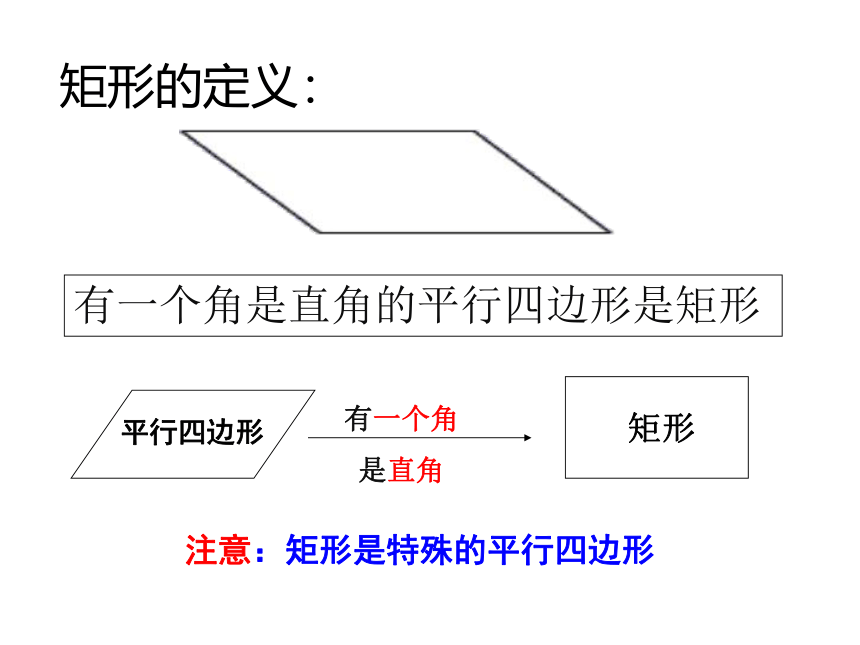
有一个角是直角的平行四边形是矩形
矩形的定义:
平行四边形
矩形
有一个角
是直角
注意:矩形是特殊的平行四边形
思考 因为矩形是平行四边形,所以它具有平行四边形的所有性质,由于它有一个角为直角,它是否具有一般平行四边形不具有的一些特殊性质呢?
可以从边,角,对角线等方面来考虑.
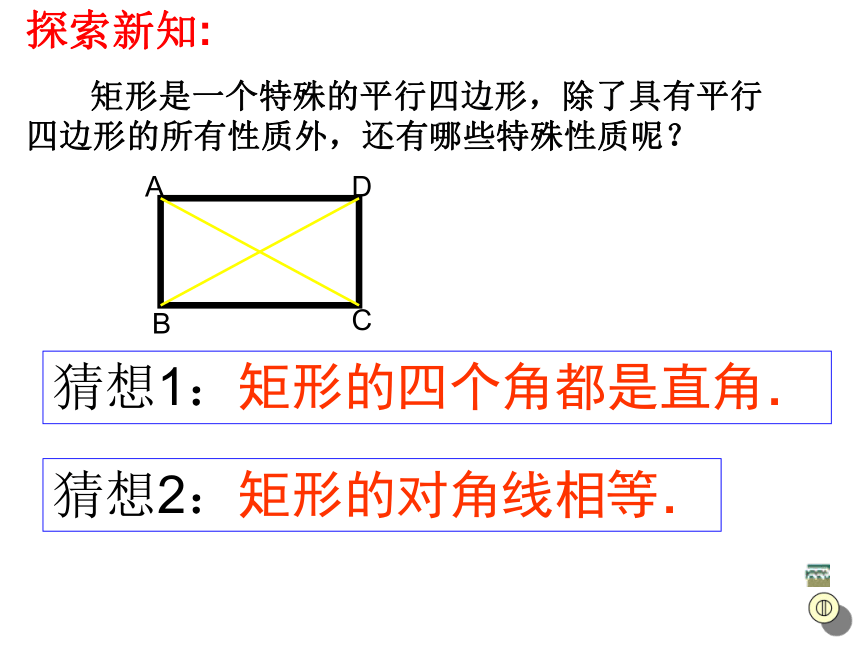
探索新知:
矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?
猜想1:矩形的四个角都是直角.
猜想2:矩形的对角线相等.
A
B
C
D
证明:∵四边形ABCD是矩形,
∴∠B=∠D,∠C=∠A, AB∥DC.
∴∠B+∠C=180°.
又∵∠B = 90°,
∴∠C = 90°.
∴∠B=∠C=∠D=∠A =90°.
A
B
C
D
求证:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°
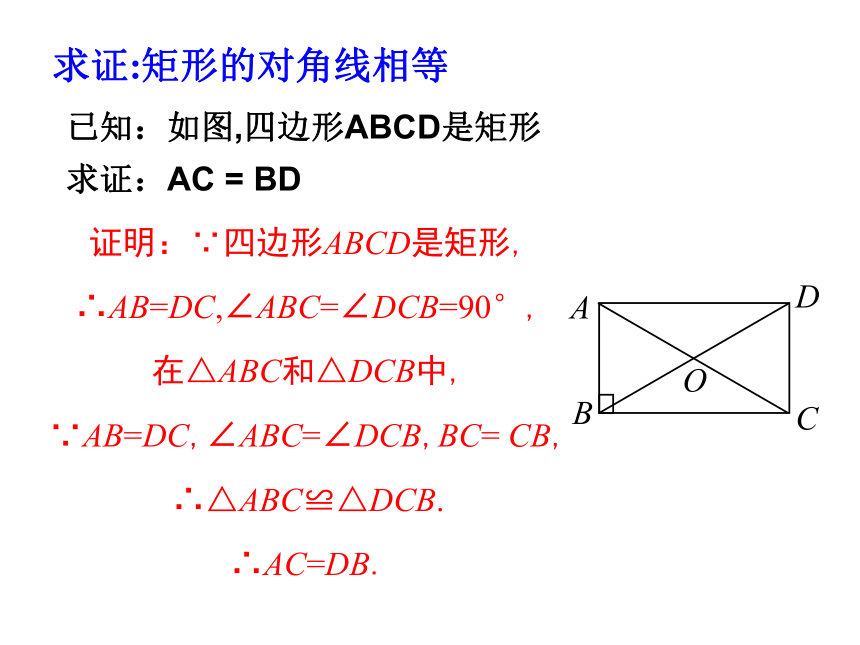
证明:∵四边形ABCD是矩形,
∴AB=DC,∠ABC=∠DCB=90°,
在△ABC和△DCB中,
∵AB=DC,∠ABC=∠DCB,BC= CB,
∴△ABC≌△DCB.
∴AC=DB.
A
B
C
D
O
已知:如图,四边形ABCD是矩形
求证:AC = BD
求证:矩形的对角线相等
矩形特殊的性质
矩形的四个角都是直角.
矩形的两条对角线相等
从角上看:
从对角线上看:
几何语言描述:
在矩形ABCD中,对角线AC与DB相交于点O.
∠ABC=∠BCD=∠CDA=∠DAB =90°,AC=DB.
A
B
C
D
O
边
对角线
角
A
B
C
D
O
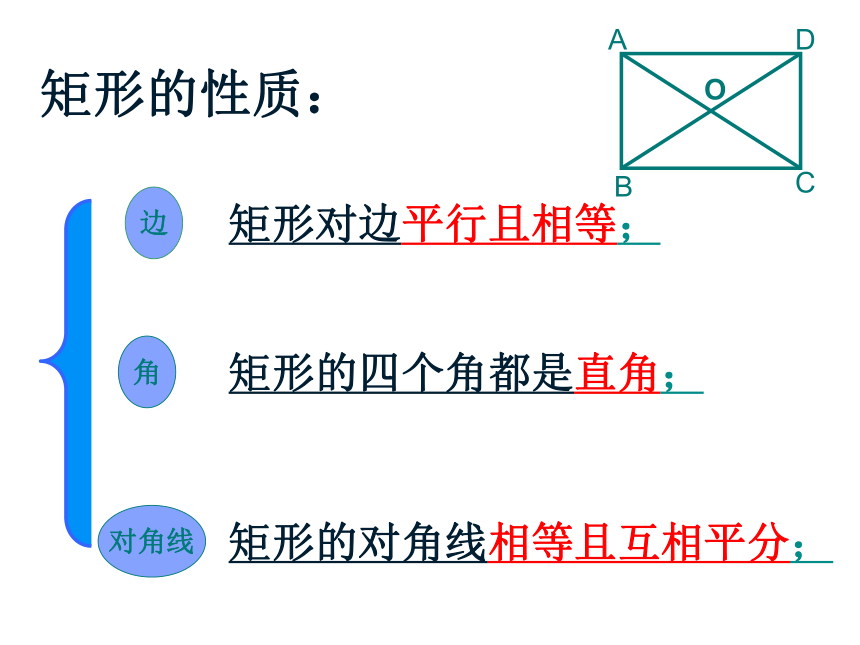
矩形对边平行且相等;
矩形的四个角都是直角;
矩形的对角线相等且互相平分;
矩形的性质:
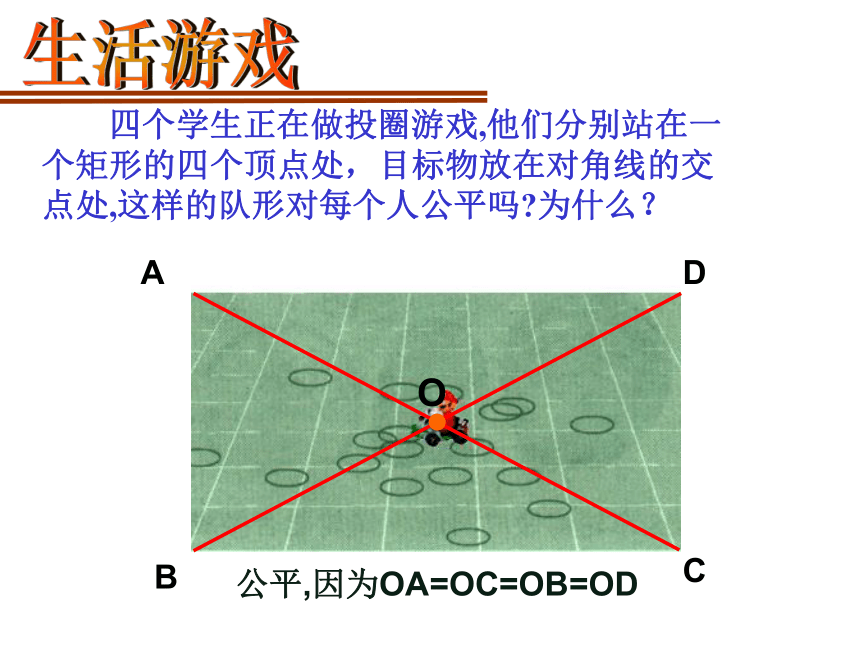
四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗?为什么?
O
A
B
C
D
公平,因为OA=OC=OB=OD
生活游戏
A
B
C
D
O
得到:直角三角形的一个性质
直角三角形斜边上的中线等于斜边的一半.
数学语言: ∵在Rt△ABC中, BO是斜边AC上的中线
∴ BO= AC
在Rt△ABC中, BO= AC
探索新知
例: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长?
方法小结: 如果矩形两对角 线的夹角是60°
或120°, 则其中必有等边三角形.
∴AC与BD相等且互相平分
∴ OA=OB
∵ ∠AOB=60°
∴ △AOB是等边三角形
∴ OA=AB=4(㎝)
∴ 矩形的对角线长 AC=BD=2OA=8(㎝)
解:∵ 四边形ABCD是矩形
D
C
B
A
o
练习:
如图,在矩形ABCD中,找出相等的线段与相等的角。
A
D
C
B
O
小试牛刀
1.矩形具有而一般平行四边形不具有的性质是 ( ) A.对角线相等 B.对边相等
C.对角相等 D.对角线互相平分
2.若直角三角形的两条直角边分别5和12,则斜边上的中线长为 ( )
A.13 B.6 C.6.5 D.不能确定
3.若矩形的一条对角线与一边的夹角为40°,则两条对角线相交的锐角是 ( )
A.20 ° B.40° C.80 ° D.10°
A
C
C
4.如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6cm,BC=8cm,则EF=______cm.
2.5
5.如图,△ABC中,E在AC上,且BE⊥AC.D为AB中点,若DE=5,AE=8,则BE的长为______.
6
第4题图
第5题图
6.如图,在矩形ABCD中,AB=6,AD=8,P是AD上的动点,PE⊥AC,PF⊥BD于F,求PE+PF的值.
解:连接OP.
∵四边形ABCD是矩形,
∴∠DAB=90°,OA=OD=OC=OB,
∴S△AOD=S△DOC=S△AOB=S△BOC
= S矩形ABCD= ×6×8=12.
在Rt△BAD中,由勾股定理得BD=10,
∴AO=OD=5,
∵S△APO+S△DPO=S△AOD,
∴ AO·PE+ DO·PF=12,即5PE+5PF=24,
∴PE+PF= .
能力提升:
矩形的相关概念及性质
具有平行四边形的一切性质
四个内角都是直角,
两条对角线互相平分且相等
轴对称图形
有两条对称轴
直角三角形斜边上的中线等于斜边的一半
有一个角是直角的平行四边形叫做矩形
本课小结
矩形的四个角都是直角.
※ 矩形的性质定理1
矩形的对角线相等.
※ 矩形的性质定理2
※ 直角三角形的一个性质
直角三角形斜边上的中线等于斜边的一半.
矩形定义:
有一个角是直角的平行四边形叫做矩形.
反思拓展:
1、工人师傅做铝合金窗框分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料(如图1),使AB=CD, EF=GH;
(2)摆放成如图(2)的四边形,则这时窗框的形状是___,根据的数学道理是___________________;
(3)将直角尺靠紧窗框的一个角(如图3)调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图4),说明窗框合格,这时窗框是____,根据的数学道理是____________________。
B
A
C
E
D
G
F
H
1
2
3
4
平行四边形
两组对边分别相等的四边形是平行四边形
矩形
有一个角是直角的
平行四边形是矩形
3. 过四边形的各个顶点分别作对角线的平行线,若这四条平行线围成一个矩形,则原四边形一定是
2. 下面性质中,矩形不一定具有的是
A.对角线相等 B.四个角都相等
C.是轴对称图形 D.对角线垂直
A.对角线相等的四边形
B.对角线互相平分且相等的四边形
C.对角线互垂直平分的四边形
D.对角线垂直的四边形
[ ]
[ ]
D
D
A.50° B.60° C.70° D.80°
5. 矩形ABCD中,AB=2BC,E在CD上,AE=AB,则∠BAE等于
A.30° B.45° C.60° D.120°
[ ]
[ ]
D
A
4. 已知矩形的一条对角线与一边的夹角是40°,则两条对角线所夹锐角的度数为
5. 如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?
A D
B C
解: ∵ △AOB、 △BOC、 △COD
和△AOD四个三角形的周长和为86cm,
又∵
AC=BD=13cm,
∴ AB+BC+CD+DA
=86-2(AC+BD)
=86-4×13=34(cm)
即矩形ABCD的周长等于34cm。
O
18.2.1 矩形
第1课时 矩形的性质
有一个角是直角的平行四边形是矩形
矩形的定义:
平行四边形
矩形
有一个角
是直角
注意:矩形是特殊的平行四边形
思考 因为矩形是平行四边形,所以它具有平行四边形的所有性质,由于它有一个角为直角,它是否具有一般平行四边形不具有的一些特殊性质呢?
可以从边,角,对角线等方面来考虑.
探索新知:
矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?
猜想1:矩形的四个角都是直角.
猜想2:矩形的对角线相等.
A
B
C
D
证明:∵四边形ABCD是矩形,
∴∠B=∠D,∠C=∠A, AB∥DC.
∴∠B+∠C=180°.
又∵∠B = 90°,
∴∠C = 90°.
∴∠B=∠C=∠D=∠A =90°.
A
B
C
D
求证:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°
证明:∵四边形ABCD是矩形,
∴AB=DC,∠ABC=∠DCB=90°,
在△ABC和△DCB中,
∵AB=DC,∠ABC=∠DCB,BC= CB,
∴△ABC≌△DCB.
∴AC=DB.
A
B
C
D
O
已知:如图,四边形ABCD是矩形
求证:AC = BD
求证:矩形的对角线相等
矩形特殊的性质
矩形的四个角都是直角.
矩形的两条对角线相等
从角上看:
从对角线上看:
几何语言描述:
在矩形ABCD中,对角线AC与DB相交于点O.
∠ABC=∠BCD=∠CDA=∠DAB =90°,AC=DB.
A
B
C
D
O
边
对角线
角
A
B
C
D
O
矩形对边平行且相等;
矩形的四个角都是直角;
矩形的对角线相等且互相平分;
矩形的性质:
四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗?为什么?
O
A
B
C
D
公平,因为OA=OC=OB=OD
生活游戏
A
B
C
D
O
得到:直角三角形的一个性质
直角三角形斜边上的中线等于斜边的一半.
数学语言: ∵在Rt△ABC中, BO是斜边AC上的中线
∴ BO= AC
在Rt△ABC中, BO= AC
探索新知
例: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长?
方法小结: 如果矩形两对角 线的夹角是60°
或120°, 则其中必有等边三角形.
∴AC与BD相等且互相平分
∴ OA=OB
∵ ∠AOB=60°
∴ △AOB是等边三角形
∴ OA=AB=4(㎝)
∴ 矩形的对角线长 AC=BD=2OA=8(㎝)
解:∵ 四边形ABCD是矩形
D
C
B
A
o
练习:
如图,在矩形ABCD中,找出相等的线段与相等的角。
A
D
C
B
O
小试牛刀
1.矩形具有而一般平行四边形不具有的性质是 ( ) A.对角线相等 B.对边相等
C.对角相等 D.对角线互相平分
2.若直角三角形的两条直角边分别5和12,则斜边上的中线长为 ( )
A.13 B.6 C.6.5 D.不能确定
3.若矩形的一条对角线与一边的夹角为40°,则两条对角线相交的锐角是 ( )
A.20 ° B.40° C.80 ° D.10°
A
C
C
4.如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6cm,BC=8cm,则EF=______cm.
2.5
5.如图,△ABC中,E在AC上,且BE⊥AC.D为AB中点,若DE=5,AE=8,则BE的长为______.
6
第4题图
第5题图
6.如图,在矩形ABCD中,AB=6,AD=8,P是AD上的动点,PE⊥AC,PF⊥BD于F,求PE+PF的值.
解:连接OP.
∵四边形ABCD是矩形,
∴∠DAB=90°,OA=OD=OC=OB,
∴S△AOD=S△DOC=S△AOB=S△BOC
= S矩形ABCD= ×6×8=12.
在Rt△BAD中,由勾股定理得BD=10,
∴AO=OD=5,
∵S△APO+S△DPO=S△AOD,
∴ AO·PE+ DO·PF=12,即5PE+5PF=24,
∴PE+PF= .
能力提升:
矩形的相关概念及性质
具有平行四边形的一切性质
四个内角都是直角,
两条对角线互相平分且相等
轴对称图形
有两条对称轴
直角三角形斜边上的中线等于斜边的一半
有一个角是直角的平行四边形叫做矩形
本课小结
矩形的四个角都是直角.
※ 矩形的性质定理1
矩形的对角线相等.
※ 矩形的性质定理2
※ 直角三角形的一个性质
直角三角形斜边上的中线等于斜边的一半.
矩形定义:
有一个角是直角的平行四边形叫做矩形.
反思拓展:
1、工人师傅做铝合金窗框分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料(如图1),使AB=CD, EF=GH;
(2)摆放成如图(2)的四边形,则这时窗框的形状是___,根据的数学道理是___________________;
(3)将直角尺靠紧窗框的一个角(如图3)调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图4),说明窗框合格,这时窗框是____,根据的数学道理是____________________。
B
A
C
E
D
G
F
H
1
2
3
4
平行四边形
两组对边分别相等的四边形是平行四边形
矩形
有一个角是直角的
平行四边形是矩形
3. 过四边形的各个顶点分别作对角线的平行线,若这四条平行线围成一个矩形,则原四边形一定是
2. 下面性质中,矩形不一定具有的是
A.对角线相等 B.四个角都相等
C.是轴对称图形 D.对角线垂直
A.对角线相等的四边形
B.对角线互相平分且相等的四边形
C.对角线互垂直平分的四边形
D.对角线垂直的四边形
[ ]
[ ]
D
D
A.50° B.60° C.70° D.80°
5. 矩形ABCD中,AB=2BC,E在CD上,AE=AB,则∠BAE等于
A.30° B.45° C.60° D.120°
[ ]
[ ]
D
A
4. 已知矩形的一条对角线与一边的夹角是40°,则两条对角线所夹锐角的度数为
5. 如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?
A D
B C
解: ∵ △AOB、 △BOC、 △COD
和△AOD四个三角形的周长和为86cm,
又∵
AC=BD=13cm,
∴ AB+BC+CD+DA
=86-2(AC+BD)
=86-4×13=34(cm)
即矩形ABCD的周长等于34cm。
O
