河北省邯郸市第十一中学2020——2021学年八年级上学期期末数学试卷(Word版 含解析)
文档属性
| 名称 | 河北省邯郸市第十一中学2020——2021学年八年级上学期期末数学试卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 263.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-10 14:41:14 | ||
图片预览




文档简介
2020-2021学年河北省邯郸十一中八年级(上)期末数学试卷
一、选择题(共16小题,1-10题每题3分,11-16题每题2分,共42分)
1.下列图形具有稳定性的是( )
A. B. C. D.
2.若□×xy=3x2y+2xy,则□内应填的式子是( )
A.3x+2 B.x+2 C.3xy+2 D.xy+2
3.如图,从标有数字1,2,3,4的四个小正方形中拿走一个,成为一个轴对称图形,则应该拿走的小正方形的标号是( )
A.1 B.2 C.3 D.4
4.如图,△ABC的BC边上的高是( )
A.BE B.AF C.CD D.CF
5.对于分式来说,当x=﹣1时,无意义,则a的值是( )
A.1 B.2 C.﹣1 D.﹣2
6.计算:(a?a3)2=a2?(a3)2=a2?a6=a8,其中,第一步运算的依据是( )
A.积的乘方法则 B.幂的乘方法则
C.乘法分配律 D.同底数幂的乘法法则
7.如图,△ABC与△DCE都是等边三角形,B,C,E三点在同一条直线上,若AB=3,∠BAD=150°,则DE的长为( )
A.3 B.4 C.5 D.6
8.根据下列条件不能唯一画出△ABC的是( )
A.AB=5,BC=6,AC=7 B.AB=5,BC=6,∠B=45°
C.AB=5,AC=4,∠C=90° D.AB=5,AC=4,∠C=45°
9.如图是A,B,C三岛的平面图,C岛在A岛的北偏东35°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西55°方向,则A,B,C三岛组成一个( )
A.等腰直角三角形 B.等腰三角形
C.直角三角形 D.等边三角形
10.如图,已知点D、E分别在∠CAB的边AB、AC上,若PD=6,由作图痕迹可得,PE的最小值是( )
A.2 B.3 C.6 D.12
11.(2分)若化简?□的最终结果是整式,则□的式子可以是( )
A.m﹣1 B.m+1 C.m D.2
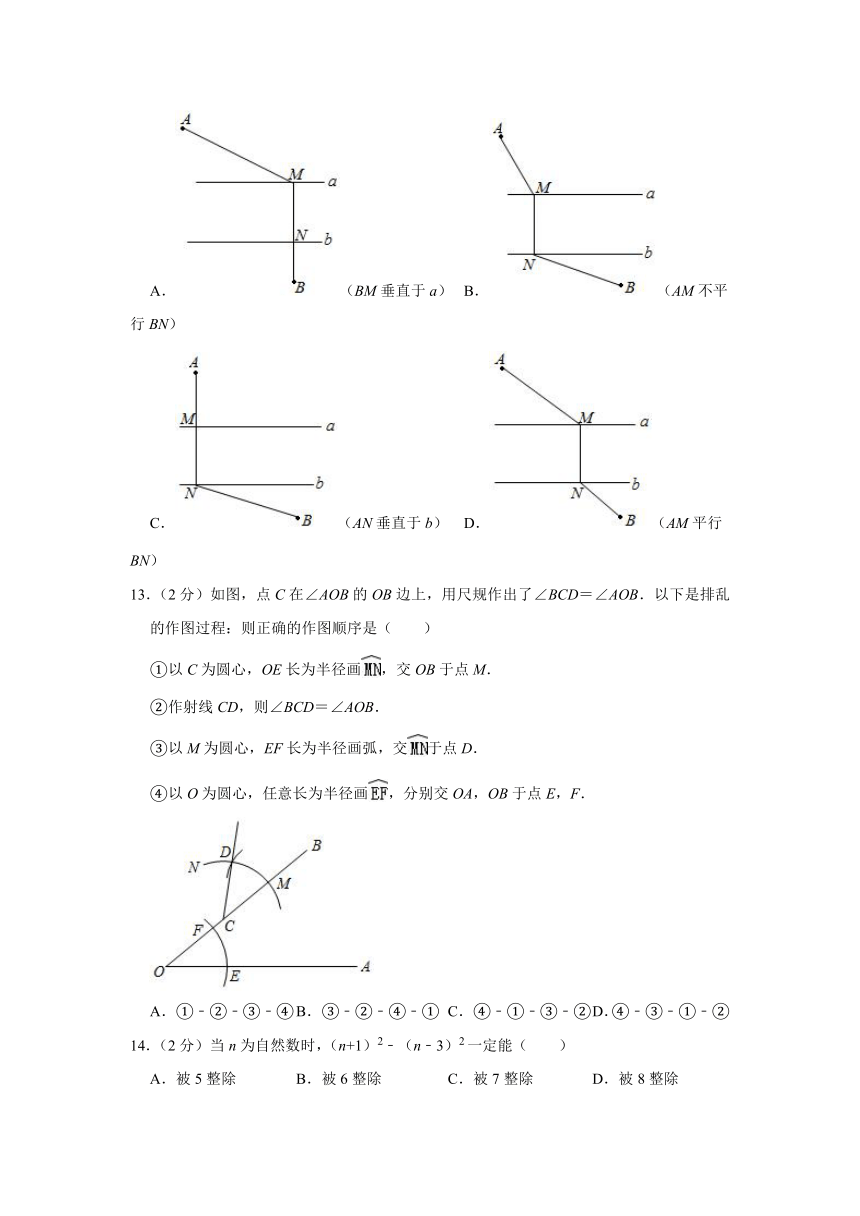
12.(2分)A和B两地在一条河的两岸,现要在河上造一座桥MN,使从A到B的路径AMNB最短的是(假定河的两岸是平行线,桥与河岸垂直)( )
A.(BM垂直于a) B.(AM不平行BN)
C.(AN垂直于b) D.(AM平行BN)
13.(2分)如图,点C在∠AOB的OB边上,用尺规作出了∠BCD=∠AOB.以下是排乱的作图过程:则正确的作图顺序是( )
①以C为圆心,OE长为半径画,交OB于点M.
②作射线CD,则∠BCD=∠AOB.
③以M为圆心,EF长为半径画弧,交于点D.
④以O为圆心,任意长为半径画,分别交OA,OB于点E,F.
A.①﹣②﹣③﹣④ B.③﹣②﹣④﹣① C.④﹣①﹣③﹣② D.④﹣③﹣①﹣②
14.(2分)当n为自然数时,(n+1)2﹣(n﹣3)2一定能( )
A.被5整除 B.被6整除 C.被7整除 D.被8整除
15.(2分)如图,将一根笔直的竹竿斜放在竖直墙角AOB中,初始位置为CD,当一端C下滑至C'时,另一端D向右滑到D',则下列说法正确的是( )
A.下滑过程中,始终有CC'=DD'
B.下滑过程中,始终有CC'≠DD'
C.若OC<OD,则下滑过程中,一定存在某个位置使得CC'=DD'
D.若OC>OD,则下滑过程中,一定存在某个位置使得CC'=DD'
16.(2分)如图,两个正方形边长分别为a,b,如果a+b=10,ab=18,则阴影部分的面积为( )
A.21 B.22 C.23 D.24
二、填空题(共3小题,17-18每题3分,19题每空2分,共12分)
17.﹣b?b3= .
18.用科学记数法表示(2.5)8(0.4)10= .
19.(6分)如图所示,在△ABC中,DE、MN是边AB、AC的垂直平分线,其垂足分别为D、M,分别交BC于E、N,且DE和MN交于点F.
(1)若∠B=20°,则∠BAE= ;
(2)若∠EAN=40°,则∠F= ;
(3)若AB=8,AC=9,设△AEN周长为m,则m的取值范围为 .
三、解答题(共66分)
20.(8分)如图,在直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5),请回答下列问题:
(1)作出△ABC关于x轴的对称图形△A1B1C1,并直接写出△A1B1C1的顶点坐标.
(2)求△A1B1C1的面积.
21.(8分)小明采用如图所示的方法作∠AOB的平分线OC:将带刻度的直角尺DEMN按如图所示摆放,使EM边与OB边重合,顶点D落在OA边上并标记出点D的位置,量出OD的长,再重新如图放置直角尺,在DN边上截取DP=OD,过点P画射线OC,则OC平分∠AOB.请判断小明的做法是否可行?并说明理由.
22.(9分)在化简(x+1)●(x﹣1)+(◆x2﹣1)题目中,●表示+,﹣,×,÷四个运算符号中的某一个,◆表示二次项的系数.
(1)若●表示“×”;
①把◆猜成1时,请化简(x+1)(x﹣1)+(x2﹣1);
②若结果是一个常数,请说明◆表示的数是几?
(2)若◆表示数﹣2,当x=1时,(x+1)●(x﹣1)+(﹣2x2﹣1)的值为﹣1,请推算●所表示的符号.
23.(9分)在一个各内角都相等的多边形中,每一个内角都比相邻外角的3倍还大20°,
(1)求这个多边形的边数;
(2)若将这个多边形剪去一个角,剩下多边形的内角和是多少?
24.(10分)发现:两个差为2的正整数的积与1的和总是一个正整数的平方.
验证:(1)9×7+1是几的平方?
(2)设较小的一个正整数为n,写出这两个正整数积与1的和,并说明它是一个正整数的平方.
延伸:两个差为4的正偶数,它们的积与常数a的和是一个正整数的平方,求a.
25.(10分)两个小组攀登一座450m高的山,第二组的攀登速度是第一组的a倍.
(1)若两个小组同时开始攀登,当a=1.2时,第二组比第一组早15min到达顶峰,求两个小组的攀登速度;
(2)元旦假期这两个小组去攀登另一座hm高的山,第二组比第一组晚出发30min,结果两组同时到达顶峰,问第二组的平均攀登速度比第一组快多少?(用含a,h的代数式表示)
26.(12分)如图1,△ABC和△ABD中,∠BAC=∠ABD=90°,点C和点D在AB的异侧,点E为AD边上的一点,且AC=AE,连接CE交直线AB于点G,过点A作AF⊥AD交直线CE于点F.
(Ⅰ)求证:△AGE≌△AFC;
(Ⅱ)若AB=AC,求证:AD=AF+BD;
(Ⅲ)如图2,若AB=AC,点C和点D在AB的同侧,题目其他条件不变,直接写出线段AD,AF,BD的数量关系 .
2020-2021学年河北省邯郸十一中八年级(上)期末数学试卷
参考答案与试题解析
一、选择题(共16小题,1-10题每题3分,11-16题每题2分,共42分)
1.下列图形具有稳定性的是( )
A. B. C. D.
【分析】根据三角形具有稳定性解答.
【解答】解:三角形、四边形、五边形及六边形中只有三角形具有稳定性.
故选:A.
2.若□×xy=3x2y+2xy,则□内应填的式子是( )
A.3x+2 B.x+2 C.3xy+2 D.xy+2
【分析】利用乘除法的关系可得□内应填的式子是:(3x2y+2xy)与xy的商,计算即可.
【解答】解:(3x2y+2xy)÷xy,
=3x+2,
故选:A.
3.如图,从标有数字1,2,3,4的四个小正方形中拿走一个,成为一个轴对称图形,则应该拿走的小正方形的标号是( )
A.1 B.2 C.3 D.4
【分析】直接利用轴对称的性质得出符合题意答案.
【解答】解:从标有数字1,2,3,4的四个小正方形中拿走2,就可以成为一个轴对称图形.
故选:B.
4.如图,△ABC的BC边上的高是( )
A.BE B.AF C.CD D.CF
【分析】根据三角形的高解答即可.
【解答】解:△ABC的BC边上的高是AF,
故选:B.
5.对于分式来说,当x=﹣1时,无意义,则a的值是( )
A.1 B.2 C.﹣1 D.﹣2
【分析】根据分式无意义分条件计算即可.
【解答】解:当x﹣a=0,即x=a时,分式无意义,
∵当x=﹣1时,分式无意义,
∴a=﹣1,
故选:C.
6.计算:(a?a3)2=a2?(a3)2=a2?a6=a8,其中,第一步运算的依据是( )
A.积的乘方法则 B.幂的乘方法则
C.乘法分配律 D.同底数幂的乘法法则
【分析】积的乘方法则:积的乘方,把每一个因式分别乘方,再把所得的幂相乘,据此判断即可.
【解答】解:(a?a3)2=a2?(a3)2的依据是积的乘方法则.
故选:A.
7.如图,△ABC与△DCE都是等边三角形,B,C,E三点在同一条直线上,若AB=3,∠BAD=150°,则DE的长为( )
A.3 B.4 C.5 D.6
【分析】根据等边三角形的性质得出AB=AC=3,DE=DC,∠BAC=∠DCE=∠ACB=60°,求出∠ACD=60°,∠CAD=90°,求出∠ADC=30°,根据很30度角的直角三角形性质得出DC=2AC,求出即可.
【解答】解:∵△ABC与△DCE都是等边三角形,AB=3,∠BAD=150°,
∴AB=AC=3,DE=DC,∠BAC=∠DCE=∠ACB=60°,
∴∠ACD=60°,∠CAD=150°﹣60°=90°,
∴∠ADC=30°,
∴DC=2AC=6,
∴DE=DC=6,
故选:D.
8.根据下列条件不能唯一画出△ABC的是( )
A.AB=5,BC=6,AC=7 B.AB=5,BC=6,∠B=45°
C.AB=5,AC=4,∠C=90° D.AB=5,AC=4,∠C=45°
【分析】判断其是否为三角形,即两边之和大于第三边,两边之差小于第三边,两边夹一角,或两角夹一边可确定三角形的形状,否则三角形并不是唯一存在,可能有多种情况存在.
【解答】解:A、∵AC与BC两边之和大于第三边,∴能作出三角形,且三边知道能唯一画出△ABC;
B、∠B是AB,BC的夹角,故能唯一画出△ABC;
C、AB=5,AC=4,∠C=90°,得出BC=3,可唯一画出△ABC;
D、AB=5,AC=4,∠C=45°,不能画出一个三角形.
故选:D.
9.如图是A,B,C三岛的平面图,C岛在A岛的北偏东35°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西55°方向,则A,B,C三岛组成一个( )
A.等腰直角三角形 B.等腰三角形
C.直角三角形 D.等边三角形
【分析】如图,过点C作CD∥AE交AB于点D,可得∠DCA=∠EAC=35°,根据AE∥BF,可得CD∥BF,可得∠BCD=∠CBF=55°,进而得△ABC是等腰直角三角形.
【解答】解:如图,过点C作CD∥AE交AB于点D,
∴∠DCA=∠EAC=35°,
∵AE∥BF,
∴CD∥BF,
∴∠BCD=∠CBF=55°,
∴∠ACB=∠ACD+∠BCD=35°+55°=90°,
∴△ABC是直角三角形.
∵∠CAD=∠EAD﹣∠CAE=80°﹣35°=45°,
∴∠ABC=180°﹣∠ACB﹣∠CAD=45°,
∴CA=CB,
∴△ABC是等腰直角三角形.
故选:A.
10.如图,已知点D、E分别在∠CAB的边AB、AC上,若PD=6,由作图痕迹可得,PE的最小值是( )
A.2 B.3 C.6 D.12
【分析】根据作图痕迹可得,AP是∠BAC的平分线,根据角平分线上的点到角的两边距离相等即可得PE的最小值.
【解答】解:根据作图痕迹可知:
AP是∠BAC的平分线,
∵PD⊥AB,且PD=6,
当PE⊥AC时,
PE=PD=6,
∴PE的最小值是6.
故选:C.
11.(2分)若化简?□的最终结果是整式,则□的式子可以是( )
A.m﹣1 B.m+1 C.m D.2
【分析】根据同分母分子的加减法法则判断即可.
【解答】解:A.=,故本选项符合题意;
B.,故本选项不合题意;
C.,故本选项不合题意;
D.,故本选项不合题意.
故选:A.
12.(2分)A和B两地在一条河的两岸,现要在河上造一座桥MN,使从A到B的路径AMNB最短的是(假定河的两岸是平行线,桥与河岸垂直)( )
A.(BM垂直于a) B.(AM不平行BN)
C.(AN垂直于b) D.(AM平行BN)
【分析】过A作河的垂线AH,要使最短,MN⊥直线a,AI=MN,连接BI即可得出N,作出AM、MN、BN即可.
【解答】解:根据垂线段最短,得出MN是河的宽时,MN最短,即MN⊥直线a(或直线b),只要AM+BN最短即可,
即过A作河岸a的垂线AH,垂足为H,在直线AH上取点I,使AI等于河宽.
连结IB交河的b边岸于N,作MN垂直于河岸交a边的岸于M点,所得MN即为所求.
故选:D.
13.(2分)如图,点C在∠AOB的OB边上,用尺规作出了∠BCD=∠AOB.以下是排乱的作图过程:则正确的作图顺序是( )
①以C为圆心,OE长为半径画,交OB于点M.
②作射线CD,则∠BCD=∠AOB.
③以M为圆心,EF长为半径画弧,交于点D.
④以O为圆心,任意长为半径画,分别交OA,OB于点E,F.
A.①﹣②﹣③﹣④ B.③﹣②﹣④﹣① C.④﹣①﹣③﹣② D.④﹣③﹣①﹣②
【分析】根据作一个角等于已知角的作图过程即可判断.
【解答】解:根据作一个角等于已知角的过程可知:
④以O为圆心,任意长为半径画,分别交OA,OB于点E,F.
①以C为圆心,OE长为半径画,交OB于点M.
③以M为圆心,EF长为半径画弧,交于点D.
②作射线CD,则∠BCD=∠AOB.
故选:C.
14.(2分)当n为自然数时,(n+1)2﹣(n﹣3)2一定能( )
A.被5整除 B.被6整除 C.被7整除 D.被8整除
【分析】将所求式子用完全平方公式展开可得原式=8(n﹣1),即可进行求解.
【解答】解:(n+1)2﹣(n﹣3)2=n2+2n+1﹣n2+6n﹣9=8n﹣8=8(n﹣1),
∴能被8整除,
故选:D.
15.(2分)如图,将一根笔直的竹竿斜放在竖直墙角AOB中,初始位置为CD,当一端C下滑至C'时,另一端D向右滑到D',则下列说法正确的是( )
A.下滑过程中,始终有CC'=DD'
B.下滑过程中,始终有CC'≠DD'
C.若OC<OD,则下滑过程中,一定存在某个位置使得CC'=DD'
D.若OC>OD,则下滑过程中,一定存在某个位置使得CC'=DD'
【分析】根据全等三角形的性质解答即可.
【解答】解:将一根笔直的竹竿斜放在竖直墙角AOB中,初始位置为CD,当一端C下滑至C'时,另一端D向右滑到D',
可得:CD=C'D',
A、下滑过程中,CC'与DD'不一定相等,说法错误;
B、下滑过程中,当△OCD与△OD'C'全等时,CC'=DD',说法错误;
C、若OC<OD,则下滑过程中,不存在某个位置使得CC'=DD',说法错误;
D、若OC>OD,则下滑过程中,当△OCD与△OD'C'全等时,一定存在某个位置使得CC'=DD',说法正确;
故选:D.
16.(2分)如图,两个正方形边长分别为a,b,如果a+b=10,ab=18,则阴影部分的面积为( )
A.21 B.22 C.23 D.24
【分析】表示出空白三角形的面积,用总面积减去两个空白三角形的面积即可,再将得到的等式变形后,利用整体代入求值即可.
【解答】解:如图,三角形②的一条直角边为a,另一条直角边为b,因此S△②=(a﹣b)b=ab﹣b2,
S△①=a2,
∴S阴影部分=S大正方形﹣S△①﹣S△②,
=a2﹣ab+b2,
=[(a+b)2﹣3ab],
=(100﹣54)
=23,
故选:C.
二、填空题(共3小题,17-18每题3分,19题每空2分,共12分)
17.﹣b?b3= ﹣b4 .
【分析】同底数幂相乘,底数不变,指数相加,据此计算即可.
【解答】解:﹣b?b3=﹣b1+3=﹣b4.
故答案为:﹣b4.
18.用科学记数法表示(2.5)8(0.4)10= 1.6×10﹣1 .
【分析】积的乘方,把每一个因式分别乘方,再把所得的幂相乘,据此化简后用科学记数法表示结果即可.
【解答】解:(2.5)8(0.4)10
=
=
=
=18×0.16
=1.6×10﹣1.
故答案为:1.6×10﹣1.
19.(6分)如图所示,在△ABC中,DE、MN是边AB、AC的垂直平分线,其垂足分别为D、M,分别交BC于E、N,且DE和MN交于点F.
(1)若∠B=20°,则∠BAE= 20° ;
(2)若∠EAN=40°,则∠F= 70° ;
(3)若AB=8,AC=9,设△AEN周长为m,则m的取值范围为 1<m<17 .
【分析】(1)根据线段垂直平分线的性质得到EA=EB,根据等腰三角形的性质解答即可;
(2)根据线段垂直平分线的性质得到EA=EB,AN=CN,根据三角形内角和定理计算即可;
(3)根据三角形的周长公式得到△AEN的周长=BC,根据三角形的三边关系计算,得到答案.
【解答】解:(1)∵DE是线段AB的垂直平分线,
∴EA=EB,
∴∠BAE=∠B=20°;
(2))∵DE、MN是边AB、AC的垂直平分线,
∴AE=BE,AN=CN,
∴∠BAE=∠B,∠CAN=∠C,
∵∠EAN=40°,∠B+∠BAE+∠EAN+∠CAN+∠C=180°,
∴∠BAE+∠CAN=70°,
∴∠BAC=∠BAE+∠CAN+∠EAN=110°,
∵∠ADF=∠AMF=90°,
∴∠F=360°﹣∠ADF﹣∠AMF﹣∠BAC=360°﹣90°﹣90°﹣110°=70°;
(3)∵DE、MN是边AB、AC的垂直平分线,
∴AE=BE,AN=CN,
∴△AEN的周长=AE+EN+AN=BE+EN+CN=BC,
在△ABC中,AB=8,AC=9,
∴9﹣8<BC<9+8,
∴1<m<17.
故答案为:(1)20°;(2)70°;(3)1<m<17.
三、解答题(共66分)
20.(8分)如图,在直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5),请回答下列问题:
(1)作出△ABC关于x轴的对称图形△A1B1C1,并直接写出△A1B1C1的顶点坐标.
(2)求△A1B1C1的面积.
【分析】(1)依据关于x轴的对称点的坐标特点:横坐标不变,纵坐标互为相反数,即可得出△A1B1C1的位置以及顶点坐标.
(2)依据割补法进行计算,即可得出△A1B1C1的面积.
【解答】解:(1)如图所示,△ABC关于x轴的对称图形△A1B1C1的顶点坐标为:A1(1,﹣4),B1(4,﹣2),C1(3,﹣5).
(2)△ABC的面积为:3×3﹣×1×2﹣×1×3﹣×2×3=9﹣1﹣1.5﹣3=3.5.
21.(8分)小明采用如图所示的方法作∠AOB的平分线OC:将带刻度的直角尺DEMN按如图所示摆放,使EM边与OB边重合,顶点D落在OA边上并标记出点D的位置,量出OD的长,再重新如图放置直角尺,在DN边上截取DP=OD,过点P画射线OC,则OC平分∠AOB.请判断小明的做法是否可行?并说明理由.
【分析】根据平行线的性质得到∠DPO=∠POM,根据等腰三角形的性质得到∠DPO=∠DOP,由等量代换得到∠POM=∠DOP,由此可判断小明的做法可行.
【解答】解:小明的做法可行.理由如下:
在直角尺DEMN中,DN∥EM,
∴∠DPO=∠POM,
∵DP=OD,
∴∠DPO=∠DOP,
∴∠POM=∠DOP,
∴OC平分∠AOB.
22.(9分)在化简(x+1)●(x﹣1)+(◆x2﹣1)题目中,●表示+,﹣,×,÷四个运算符号中的某一个,◆表示二次项的系数.
(1)若●表示“×”;
①把◆猜成1时,请化简(x+1)(x﹣1)+(x2﹣1);
②若结果是一个常数,请说明◆表示的数是几?
(2)若◆表示数﹣2,当x=1时,(x+1)●(x﹣1)+(﹣2x2﹣1)的值为﹣1,请推算●所表示的符号.
【分析】(1)①原式利用平方差公式化简,去括号合并即可得到结果;
②原式化简后,根据结果为常数,确定出◆表示的数即可;
(2)把x=1代入原式,使其值为﹣1,确定出●所表示的符号即可.
【解答】解:(1)①(x+1)(x﹣1)+(x2﹣1)=x2﹣1+x2﹣1=2x2﹣2;
②原式=x2﹣1+◆x2﹣1=(1+◆)x2﹣2,
若结果是一个常数,1+◆=0,
则◆=﹣1;
(2)把x=1代入得,2●0+(﹣2﹣1)=﹣1,
整理得:2●0=2,
则●为+或﹣.
23.(9分)在一个各内角都相等的多边形中,每一个内角都比相邻外角的3倍还大20°,
(1)求这个多边形的边数;
(2)若将这个多边形剪去一个角,剩下多边形的内角和是多少?
【分析】(1)设多边形的一个外角为α,则与其相邻的内角等于3α+20°,根据内角与其相邻的外角的和是180度列出方程,求出α的值,再由多边形的外角和为360°,求出此多边形的边数为360°÷α;
(2)剪掉一个角以后,多边形的边数可能增加了1条,也可能减少了1条,或者不变.根据多边形的内角和定理可以知道,边数增加1,相应内角和就增加180度,由此即可求出答案.
【解答】解:(1)设多边形的一个外角为α,则与其相邻的内角等于3α+20°,
由题意,得(3α+20)+α=180°,解得α=40°.
即多边形的每个外角为40°.
又∵多边形的外角和为360°,
∴多边形的外角个数==9.
∴多边形的边数=9,
答:这个多边形的边数是9;
(2)因为剪掉一个角以后,多边形的边数可能增加了1条,也可能减少了1条,或者不变,
当截线为经过对角2个顶点的直线时,多边形的边数减少了1条边,内角和=(9﹣2﹣1)×180°=1080°;
当截线为经过多边形一组对边的直线时,多边形的边数不变,内角和=(9﹣2)×180°=1260°;
当截线为只经过正方形一组邻边的一条直线时,多边形的边数增加一条边,内角和=(9﹣2+1)×180°=1440°.
答:将这个多边形剪去一个角,剩下多边形的内角和是1080°或1260°或1440°.
24.(10分)发现:两个差为2的正整数的积与1的和总是一个正整数的平方.
验证:(1)9×7+1是几的平方?
(2)设较小的一个正整数为n,写出这两个正整数积与1的和,并说明它是一个正整数的平方.
延伸:两个差为4的正偶数,它们的积与常数a的和是一个正整数的平方,求a.
【分析】(1)计算9×7+1,即可求解;
(2)设较小的一个正整数为n,那么这两个正整数积与1的和即为(n+2)×n+1,计算即可求解;
延伸解:设较小的正偶数为2k,计算2k(2k+4)+a=4k2+8k+a=,求出a=4.
【解答】解:(1)∵9×7+1=64=82,
∴9×7+1是8的平方;
(2)和为(n+2)×n+1,
∵(n+2)×n+1=n2+2n+1=(n+1)2,
∴原式为正整数(n+1)的平方;
延伸:设较小的正偶数为2k,
∴2k(2k+4)+a=4k2+8k+a=,
由配方法可知a=4,
原式=4(k2+2k+1)=[2(k+1)]2,
综上:a=4.
25.(10分)两个小组攀登一座450m高的山,第二组的攀登速度是第一组的a倍.
(1)若两个小组同时开始攀登,当a=1.2时,第二组比第一组早15min到达顶峰,求两个小组的攀登速度;
(2)元旦假期这两个小组去攀登另一座hm高的山,第二组比第一组晚出发30min,结果两组同时到达顶峰,问第二组的平均攀登速度比第一组快多少?(用含a,h的代数式表示)
【分析】(1)设第一组的速度为xm/min,则第二组的速度为1.2xm/min,根据两个小组同时开始攀登,第二组比第一组早15min,列方程求解.
(2)设第一组的速度为ym/min,则第二组的速度为aym/min,根据两个小组去攀登另一座hm高的山,第二组比第一组晚出发30min,结果两组同时到达顶峰,列方程求解.
【解答】解:(1)设第一组的速度为xm/min,则第二组的速度为1.2xm/min,
由题意得,﹣=15,
解得:x=5,
经检验:x=5是原分式方程的解,且符合题意,
则1.2x=6.
答:第一组的攀登速度5m/min,第二组的攀登速度6m/min;
(2)设第一组的平均速度为ym/min,则第二组的平均速度为aym/min,
由题意得,﹣=30,
解得:y=,
经检验:y=是原分式方程的解,且符合题意,
则ay﹣y=﹣=,
答:第二组的平均攀登速度比第一组快m/min.
26.(12分)如图1,△ABC和△ABD中,∠BAC=∠ABD=90°,点C和点D在AB的异侧,点E为AD边上的一点,且AC=AE,连接CE交直线AB于点G,过点A作AF⊥AD交直线CE于点F.
(Ⅰ)求证:△AGE≌△AFC;
(Ⅱ)若AB=AC,求证:AD=AF+BD;
(Ⅲ)如图2,若AB=AC,点C和点D在AB的同侧,题目其他条件不变,直接写出线段AD,AF,BD的数量关系 AF=AD+BD .
【分析】(Ⅰ)先判断出∠ACF=∠AEG,再用同角的余角相等判断出∠CAF=∠EAG,即可得出结论;
(Ⅱ)先用ASA判断出△ACM≌△ABD,得出AM=AD,CM=BD,由(Ⅰ)知,△AGE≌△AFC,得出∠AGE=∠AFC,再判断出CM∥AB,得出∠MCF=∠AGC,进而判断出MF=CM,即可得出结论;
(Ⅲ)同(Ⅱ)的方法,即可得出结论.
【解答】解:(Ⅰ)∵AC=AE,
∴∠ACF=∠AEG,
∵AF⊥AD,
∴∠DAF=90°=∠CAB,
∴∠DAF﹣∠FAG=∠CAB﹣∠FAG,
∴∠CAF=∠EAG,
在△AGE和△AFC中,
,
∴△AGE≌△AFC(ASA);
(Ⅱ)如图1,
过点C作CM⊥AC,交AF延长线于点M,
∴∠ACM=90°=∠ABD,
由(Ⅰ)知,∠CAF=∠EAB,
在△ACM和△ABD中,
,
∴△ACM≌△ABD(ASA),
∴AM=AD,CM=BD,
由(Ⅰ)知,△AGE≌△AFC,
∴∠AGE=∠AFC,
∴180°﹣∠AGE=180°﹣∠AFC,
∴∠AGC=∠AFG,
∵∠CFM=∠AFG,
∴∠AGC=∠CFM,
∵∠BAC=90°=∠ACM,
∴∠BAC+∠ACM=180°,
∴CM∥AB,
∴∠MCF=∠AGC,
∴∠CFM=∠MCF,
∴MF=CM,
∴AM=AF+CM,
∴AD=AF+BD;
(Ⅲ)AD=AF﹣BD;
过点C作CM⊥AC,交AF于点M,
∴∠ACM=90°=∠ABD,
由(Ⅰ)知,∠CAF=∠EAB,
在△ACM和△ABD中,
,
∴△ACM≌△ABD(ASA),
∴AM=AD,CM=BD,
由(Ⅰ)知,△AGE≌△AFC,
∴∠G=∠F,
∵∠BAC=90°=∠ACM,
∴CM∥AB,
∴∠MCF=∠G,
∴∠F=∠MCF,
∴MF=CM,
∴AF=AM+CM=AD+BD,
故答案为:AF=AD+BD.
一、选择题(共16小题,1-10题每题3分,11-16题每题2分,共42分)
1.下列图形具有稳定性的是( )
A. B. C. D.
2.若□×xy=3x2y+2xy,则□内应填的式子是( )
A.3x+2 B.x+2 C.3xy+2 D.xy+2
3.如图,从标有数字1,2,3,4的四个小正方形中拿走一个,成为一个轴对称图形,则应该拿走的小正方形的标号是( )
A.1 B.2 C.3 D.4
4.如图,△ABC的BC边上的高是( )
A.BE B.AF C.CD D.CF
5.对于分式来说,当x=﹣1时,无意义,则a的值是( )
A.1 B.2 C.﹣1 D.﹣2
6.计算:(a?a3)2=a2?(a3)2=a2?a6=a8,其中,第一步运算的依据是( )
A.积的乘方法则 B.幂的乘方法则
C.乘法分配律 D.同底数幂的乘法法则
7.如图,△ABC与△DCE都是等边三角形,B,C,E三点在同一条直线上,若AB=3,∠BAD=150°,则DE的长为( )
A.3 B.4 C.5 D.6
8.根据下列条件不能唯一画出△ABC的是( )
A.AB=5,BC=6,AC=7 B.AB=5,BC=6,∠B=45°
C.AB=5,AC=4,∠C=90° D.AB=5,AC=4,∠C=45°
9.如图是A,B,C三岛的平面图,C岛在A岛的北偏东35°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西55°方向,则A,B,C三岛组成一个( )
A.等腰直角三角形 B.等腰三角形
C.直角三角形 D.等边三角形
10.如图,已知点D、E分别在∠CAB的边AB、AC上,若PD=6,由作图痕迹可得,PE的最小值是( )
A.2 B.3 C.6 D.12
11.(2分)若化简?□的最终结果是整式,则□的式子可以是( )
A.m﹣1 B.m+1 C.m D.2
12.(2分)A和B两地在一条河的两岸,现要在河上造一座桥MN,使从A到B的路径AMNB最短的是(假定河的两岸是平行线,桥与河岸垂直)( )
A.(BM垂直于a) B.(AM不平行BN)
C.(AN垂直于b) D.(AM平行BN)
13.(2分)如图,点C在∠AOB的OB边上,用尺规作出了∠BCD=∠AOB.以下是排乱的作图过程:则正确的作图顺序是( )
①以C为圆心,OE长为半径画,交OB于点M.
②作射线CD,则∠BCD=∠AOB.
③以M为圆心,EF长为半径画弧,交于点D.
④以O为圆心,任意长为半径画,分别交OA,OB于点E,F.
A.①﹣②﹣③﹣④ B.③﹣②﹣④﹣① C.④﹣①﹣③﹣② D.④﹣③﹣①﹣②
14.(2分)当n为自然数时,(n+1)2﹣(n﹣3)2一定能( )
A.被5整除 B.被6整除 C.被7整除 D.被8整除
15.(2分)如图,将一根笔直的竹竿斜放在竖直墙角AOB中,初始位置为CD,当一端C下滑至C'时,另一端D向右滑到D',则下列说法正确的是( )
A.下滑过程中,始终有CC'=DD'
B.下滑过程中,始终有CC'≠DD'
C.若OC<OD,则下滑过程中,一定存在某个位置使得CC'=DD'
D.若OC>OD,则下滑过程中,一定存在某个位置使得CC'=DD'
16.(2分)如图,两个正方形边长分别为a,b,如果a+b=10,ab=18,则阴影部分的面积为( )
A.21 B.22 C.23 D.24
二、填空题(共3小题,17-18每题3分,19题每空2分,共12分)
17.﹣b?b3= .
18.用科学记数法表示(2.5)8(0.4)10= .
19.(6分)如图所示,在△ABC中,DE、MN是边AB、AC的垂直平分线,其垂足分别为D、M,分别交BC于E、N,且DE和MN交于点F.
(1)若∠B=20°,则∠BAE= ;
(2)若∠EAN=40°,则∠F= ;
(3)若AB=8,AC=9,设△AEN周长为m,则m的取值范围为 .
三、解答题(共66分)
20.(8分)如图,在直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5),请回答下列问题:
(1)作出△ABC关于x轴的对称图形△A1B1C1,并直接写出△A1B1C1的顶点坐标.
(2)求△A1B1C1的面积.
21.(8分)小明采用如图所示的方法作∠AOB的平分线OC:将带刻度的直角尺DEMN按如图所示摆放,使EM边与OB边重合,顶点D落在OA边上并标记出点D的位置,量出OD的长,再重新如图放置直角尺,在DN边上截取DP=OD,过点P画射线OC,则OC平分∠AOB.请判断小明的做法是否可行?并说明理由.
22.(9分)在化简(x+1)●(x﹣1)+(◆x2﹣1)题目中,●表示+,﹣,×,÷四个运算符号中的某一个,◆表示二次项的系数.
(1)若●表示“×”;
①把◆猜成1时,请化简(x+1)(x﹣1)+(x2﹣1);
②若结果是一个常数,请说明◆表示的数是几?
(2)若◆表示数﹣2,当x=1时,(x+1)●(x﹣1)+(﹣2x2﹣1)的值为﹣1,请推算●所表示的符号.
23.(9分)在一个各内角都相等的多边形中,每一个内角都比相邻外角的3倍还大20°,
(1)求这个多边形的边数;
(2)若将这个多边形剪去一个角,剩下多边形的内角和是多少?
24.(10分)发现:两个差为2的正整数的积与1的和总是一个正整数的平方.
验证:(1)9×7+1是几的平方?
(2)设较小的一个正整数为n,写出这两个正整数积与1的和,并说明它是一个正整数的平方.
延伸:两个差为4的正偶数,它们的积与常数a的和是一个正整数的平方,求a.
25.(10分)两个小组攀登一座450m高的山,第二组的攀登速度是第一组的a倍.
(1)若两个小组同时开始攀登,当a=1.2时,第二组比第一组早15min到达顶峰,求两个小组的攀登速度;
(2)元旦假期这两个小组去攀登另一座hm高的山,第二组比第一组晚出发30min,结果两组同时到达顶峰,问第二组的平均攀登速度比第一组快多少?(用含a,h的代数式表示)
26.(12分)如图1,△ABC和△ABD中,∠BAC=∠ABD=90°,点C和点D在AB的异侧,点E为AD边上的一点,且AC=AE,连接CE交直线AB于点G,过点A作AF⊥AD交直线CE于点F.
(Ⅰ)求证:△AGE≌△AFC;
(Ⅱ)若AB=AC,求证:AD=AF+BD;
(Ⅲ)如图2,若AB=AC,点C和点D在AB的同侧,题目其他条件不变,直接写出线段AD,AF,BD的数量关系 .
2020-2021学年河北省邯郸十一中八年级(上)期末数学试卷
参考答案与试题解析
一、选择题(共16小题,1-10题每题3分,11-16题每题2分,共42分)
1.下列图形具有稳定性的是( )
A. B. C. D.
【分析】根据三角形具有稳定性解答.
【解答】解:三角形、四边形、五边形及六边形中只有三角形具有稳定性.
故选:A.
2.若□×xy=3x2y+2xy,则□内应填的式子是( )
A.3x+2 B.x+2 C.3xy+2 D.xy+2
【分析】利用乘除法的关系可得□内应填的式子是:(3x2y+2xy)与xy的商,计算即可.
【解答】解:(3x2y+2xy)÷xy,
=3x+2,
故选:A.
3.如图,从标有数字1,2,3,4的四个小正方形中拿走一个,成为一个轴对称图形,则应该拿走的小正方形的标号是( )
A.1 B.2 C.3 D.4
【分析】直接利用轴对称的性质得出符合题意答案.
【解答】解:从标有数字1,2,3,4的四个小正方形中拿走2,就可以成为一个轴对称图形.
故选:B.
4.如图,△ABC的BC边上的高是( )
A.BE B.AF C.CD D.CF
【分析】根据三角形的高解答即可.
【解答】解:△ABC的BC边上的高是AF,
故选:B.
5.对于分式来说,当x=﹣1时,无意义,则a的值是( )
A.1 B.2 C.﹣1 D.﹣2
【分析】根据分式无意义分条件计算即可.
【解答】解:当x﹣a=0,即x=a时,分式无意义,
∵当x=﹣1时,分式无意义,
∴a=﹣1,
故选:C.
6.计算:(a?a3)2=a2?(a3)2=a2?a6=a8,其中,第一步运算的依据是( )
A.积的乘方法则 B.幂的乘方法则
C.乘法分配律 D.同底数幂的乘法法则
【分析】积的乘方法则:积的乘方,把每一个因式分别乘方,再把所得的幂相乘,据此判断即可.
【解答】解:(a?a3)2=a2?(a3)2的依据是积的乘方法则.
故选:A.
7.如图,△ABC与△DCE都是等边三角形,B,C,E三点在同一条直线上,若AB=3,∠BAD=150°,则DE的长为( )
A.3 B.4 C.5 D.6
【分析】根据等边三角形的性质得出AB=AC=3,DE=DC,∠BAC=∠DCE=∠ACB=60°,求出∠ACD=60°,∠CAD=90°,求出∠ADC=30°,根据很30度角的直角三角形性质得出DC=2AC,求出即可.
【解答】解:∵△ABC与△DCE都是等边三角形,AB=3,∠BAD=150°,
∴AB=AC=3,DE=DC,∠BAC=∠DCE=∠ACB=60°,
∴∠ACD=60°,∠CAD=150°﹣60°=90°,
∴∠ADC=30°,
∴DC=2AC=6,
∴DE=DC=6,
故选:D.
8.根据下列条件不能唯一画出△ABC的是( )
A.AB=5,BC=6,AC=7 B.AB=5,BC=6,∠B=45°
C.AB=5,AC=4,∠C=90° D.AB=5,AC=4,∠C=45°
【分析】判断其是否为三角形,即两边之和大于第三边,两边之差小于第三边,两边夹一角,或两角夹一边可确定三角形的形状,否则三角形并不是唯一存在,可能有多种情况存在.
【解答】解:A、∵AC与BC两边之和大于第三边,∴能作出三角形,且三边知道能唯一画出△ABC;
B、∠B是AB,BC的夹角,故能唯一画出△ABC;
C、AB=5,AC=4,∠C=90°,得出BC=3,可唯一画出△ABC;
D、AB=5,AC=4,∠C=45°,不能画出一个三角形.
故选:D.
9.如图是A,B,C三岛的平面图,C岛在A岛的北偏东35°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西55°方向,则A,B,C三岛组成一个( )
A.等腰直角三角形 B.等腰三角形
C.直角三角形 D.等边三角形
【分析】如图,过点C作CD∥AE交AB于点D,可得∠DCA=∠EAC=35°,根据AE∥BF,可得CD∥BF,可得∠BCD=∠CBF=55°,进而得△ABC是等腰直角三角形.
【解答】解:如图,过点C作CD∥AE交AB于点D,
∴∠DCA=∠EAC=35°,
∵AE∥BF,
∴CD∥BF,
∴∠BCD=∠CBF=55°,
∴∠ACB=∠ACD+∠BCD=35°+55°=90°,
∴△ABC是直角三角形.
∵∠CAD=∠EAD﹣∠CAE=80°﹣35°=45°,
∴∠ABC=180°﹣∠ACB﹣∠CAD=45°,
∴CA=CB,
∴△ABC是等腰直角三角形.
故选:A.
10.如图,已知点D、E分别在∠CAB的边AB、AC上,若PD=6,由作图痕迹可得,PE的最小值是( )
A.2 B.3 C.6 D.12
【分析】根据作图痕迹可得,AP是∠BAC的平分线,根据角平分线上的点到角的两边距离相等即可得PE的最小值.
【解答】解:根据作图痕迹可知:
AP是∠BAC的平分线,
∵PD⊥AB,且PD=6,
当PE⊥AC时,
PE=PD=6,
∴PE的最小值是6.
故选:C.
11.(2分)若化简?□的最终结果是整式,则□的式子可以是( )
A.m﹣1 B.m+1 C.m D.2
【分析】根据同分母分子的加减法法则判断即可.
【解答】解:A.=,故本选项符合题意;
B.,故本选项不合题意;
C.,故本选项不合题意;
D.,故本选项不合题意.
故选:A.
12.(2分)A和B两地在一条河的两岸,现要在河上造一座桥MN,使从A到B的路径AMNB最短的是(假定河的两岸是平行线,桥与河岸垂直)( )
A.(BM垂直于a) B.(AM不平行BN)
C.(AN垂直于b) D.(AM平行BN)
【分析】过A作河的垂线AH,要使最短,MN⊥直线a,AI=MN,连接BI即可得出N,作出AM、MN、BN即可.
【解答】解:根据垂线段最短,得出MN是河的宽时,MN最短,即MN⊥直线a(或直线b),只要AM+BN最短即可,
即过A作河岸a的垂线AH,垂足为H,在直线AH上取点I,使AI等于河宽.
连结IB交河的b边岸于N,作MN垂直于河岸交a边的岸于M点,所得MN即为所求.
故选:D.
13.(2分)如图,点C在∠AOB的OB边上,用尺规作出了∠BCD=∠AOB.以下是排乱的作图过程:则正确的作图顺序是( )
①以C为圆心,OE长为半径画,交OB于点M.
②作射线CD,则∠BCD=∠AOB.
③以M为圆心,EF长为半径画弧,交于点D.
④以O为圆心,任意长为半径画,分别交OA,OB于点E,F.
A.①﹣②﹣③﹣④ B.③﹣②﹣④﹣① C.④﹣①﹣③﹣② D.④﹣③﹣①﹣②
【分析】根据作一个角等于已知角的作图过程即可判断.
【解答】解:根据作一个角等于已知角的过程可知:
④以O为圆心,任意长为半径画,分别交OA,OB于点E,F.
①以C为圆心,OE长为半径画,交OB于点M.
③以M为圆心,EF长为半径画弧,交于点D.
②作射线CD,则∠BCD=∠AOB.
故选:C.
14.(2分)当n为自然数时,(n+1)2﹣(n﹣3)2一定能( )
A.被5整除 B.被6整除 C.被7整除 D.被8整除
【分析】将所求式子用完全平方公式展开可得原式=8(n﹣1),即可进行求解.
【解答】解:(n+1)2﹣(n﹣3)2=n2+2n+1﹣n2+6n﹣9=8n﹣8=8(n﹣1),
∴能被8整除,
故选:D.
15.(2分)如图,将一根笔直的竹竿斜放在竖直墙角AOB中,初始位置为CD,当一端C下滑至C'时,另一端D向右滑到D',则下列说法正确的是( )
A.下滑过程中,始终有CC'=DD'
B.下滑过程中,始终有CC'≠DD'
C.若OC<OD,则下滑过程中,一定存在某个位置使得CC'=DD'
D.若OC>OD,则下滑过程中,一定存在某个位置使得CC'=DD'
【分析】根据全等三角形的性质解答即可.
【解答】解:将一根笔直的竹竿斜放在竖直墙角AOB中,初始位置为CD,当一端C下滑至C'时,另一端D向右滑到D',
可得:CD=C'D',
A、下滑过程中,CC'与DD'不一定相等,说法错误;
B、下滑过程中,当△OCD与△OD'C'全等时,CC'=DD',说法错误;
C、若OC<OD,则下滑过程中,不存在某个位置使得CC'=DD',说法错误;
D、若OC>OD,则下滑过程中,当△OCD与△OD'C'全等时,一定存在某个位置使得CC'=DD',说法正确;
故选:D.
16.(2分)如图,两个正方形边长分别为a,b,如果a+b=10,ab=18,则阴影部分的面积为( )
A.21 B.22 C.23 D.24
【分析】表示出空白三角形的面积,用总面积减去两个空白三角形的面积即可,再将得到的等式变形后,利用整体代入求值即可.
【解答】解:如图,三角形②的一条直角边为a,另一条直角边为b,因此S△②=(a﹣b)b=ab﹣b2,
S△①=a2,
∴S阴影部分=S大正方形﹣S△①﹣S△②,
=a2﹣ab+b2,
=[(a+b)2﹣3ab],
=(100﹣54)
=23,
故选:C.
二、填空题(共3小题,17-18每题3分,19题每空2分,共12分)
17.﹣b?b3= ﹣b4 .
【分析】同底数幂相乘,底数不变,指数相加,据此计算即可.
【解答】解:﹣b?b3=﹣b1+3=﹣b4.
故答案为:﹣b4.
18.用科学记数法表示(2.5)8(0.4)10= 1.6×10﹣1 .
【分析】积的乘方,把每一个因式分别乘方,再把所得的幂相乘,据此化简后用科学记数法表示结果即可.
【解答】解:(2.5)8(0.4)10
=
=
=
=18×0.16
=1.6×10﹣1.
故答案为:1.6×10﹣1.
19.(6分)如图所示,在△ABC中,DE、MN是边AB、AC的垂直平分线,其垂足分别为D、M,分别交BC于E、N,且DE和MN交于点F.
(1)若∠B=20°,则∠BAE= 20° ;
(2)若∠EAN=40°,则∠F= 70° ;
(3)若AB=8,AC=9,设△AEN周长为m,则m的取值范围为 1<m<17 .
【分析】(1)根据线段垂直平分线的性质得到EA=EB,根据等腰三角形的性质解答即可;
(2)根据线段垂直平分线的性质得到EA=EB,AN=CN,根据三角形内角和定理计算即可;
(3)根据三角形的周长公式得到△AEN的周长=BC,根据三角形的三边关系计算,得到答案.
【解答】解:(1)∵DE是线段AB的垂直平分线,
∴EA=EB,
∴∠BAE=∠B=20°;
(2))∵DE、MN是边AB、AC的垂直平分线,
∴AE=BE,AN=CN,
∴∠BAE=∠B,∠CAN=∠C,
∵∠EAN=40°,∠B+∠BAE+∠EAN+∠CAN+∠C=180°,
∴∠BAE+∠CAN=70°,
∴∠BAC=∠BAE+∠CAN+∠EAN=110°,
∵∠ADF=∠AMF=90°,
∴∠F=360°﹣∠ADF﹣∠AMF﹣∠BAC=360°﹣90°﹣90°﹣110°=70°;
(3)∵DE、MN是边AB、AC的垂直平分线,
∴AE=BE,AN=CN,
∴△AEN的周长=AE+EN+AN=BE+EN+CN=BC,
在△ABC中,AB=8,AC=9,
∴9﹣8<BC<9+8,
∴1<m<17.
故答案为:(1)20°;(2)70°;(3)1<m<17.
三、解答题(共66分)
20.(8分)如图,在直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5),请回答下列问题:
(1)作出△ABC关于x轴的对称图形△A1B1C1,并直接写出△A1B1C1的顶点坐标.
(2)求△A1B1C1的面积.
【分析】(1)依据关于x轴的对称点的坐标特点:横坐标不变,纵坐标互为相反数,即可得出△A1B1C1的位置以及顶点坐标.
(2)依据割补法进行计算,即可得出△A1B1C1的面积.
【解答】解:(1)如图所示,△ABC关于x轴的对称图形△A1B1C1的顶点坐标为:A1(1,﹣4),B1(4,﹣2),C1(3,﹣5).
(2)△ABC的面积为:3×3﹣×1×2﹣×1×3﹣×2×3=9﹣1﹣1.5﹣3=3.5.
21.(8分)小明采用如图所示的方法作∠AOB的平分线OC:将带刻度的直角尺DEMN按如图所示摆放,使EM边与OB边重合,顶点D落在OA边上并标记出点D的位置,量出OD的长,再重新如图放置直角尺,在DN边上截取DP=OD,过点P画射线OC,则OC平分∠AOB.请判断小明的做法是否可行?并说明理由.
【分析】根据平行线的性质得到∠DPO=∠POM,根据等腰三角形的性质得到∠DPO=∠DOP,由等量代换得到∠POM=∠DOP,由此可判断小明的做法可行.
【解答】解:小明的做法可行.理由如下:
在直角尺DEMN中,DN∥EM,
∴∠DPO=∠POM,
∵DP=OD,
∴∠DPO=∠DOP,
∴∠POM=∠DOP,
∴OC平分∠AOB.
22.(9分)在化简(x+1)●(x﹣1)+(◆x2﹣1)题目中,●表示+,﹣,×,÷四个运算符号中的某一个,◆表示二次项的系数.
(1)若●表示“×”;
①把◆猜成1时,请化简(x+1)(x﹣1)+(x2﹣1);
②若结果是一个常数,请说明◆表示的数是几?
(2)若◆表示数﹣2,当x=1时,(x+1)●(x﹣1)+(﹣2x2﹣1)的值为﹣1,请推算●所表示的符号.
【分析】(1)①原式利用平方差公式化简,去括号合并即可得到结果;
②原式化简后,根据结果为常数,确定出◆表示的数即可;
(2)把x=1代入原式,使其值为﹣1,确定出●所表示的符号即可.
【解答】解:(1)①(x+1)(x﹣1)+(x2﹣1)=x2﹣1+x2﹣1=2x2﹣2;
②原式=x2﹣1+◆x2﹣1=(1+◆)x2﹣2,
若结果是一个常数,1+◆=0,
则◆=﹣1;
(2)把x=1代入得,2●0+(﹣2﹣1)=﹣1,
整理得:2●0=2,
则●为+或﹣.
23.(9分)在一个各内角都相等的多边形中,每一个内角都比相邻外角的3倍还大20°,
(1)求这个多边形的边数;
(2)若将这个多边形剪去一个角,剩下多边形的内角和是多少?
【分析】(1)设多边形的一个外角为α,则与其相邻的内角等于3α+20°,根据内角与其相邻的外角的和是180度列出方程,求出α的值,再由多边形的外角和为360°,求出此多边形的边数为360°÷α;
(2)剪掉一个角以后,多边形的边数可能增加了1条,也可能减少了1条,或者不变.根据多边形的内角和定理可以知道,边数增加1,相应内角和就增加180度,由此即可求出答案.
【解答】解:(1)设多边形的一个外角为α,则与其相邻的内角等于3α+20°,
由题意,得(3α+20)+α=180°,解得α=40°.
即多边形的每个外角为40°.
又∵多边形的外角和为360°,
∴多边形的外角个数==9.
∴多边形的边数=9,
答:这个多边形的边数是9;
(2)因为剪掉一个角以后,多边形的边数可能增加了1条,也可能减少了1条,或者不变,
当截线为经过对角2个顶点的直线时,多边形的边数减少了1条边,内角和=(9﹣2﹣1)×180°=1080°;
当截线为经过多边形一组对边的直线时,多边形的边数不变,内角和=(9﹣2)×180°=1260°;
当截线为只经过正方形一组邻边的一条直线时,多边形的边数增加一条边,内角和=(9﹣2+1)×180°=1440°.
答:将这个多边形剪去一个角,剩下多边形的内角和是1080°或1260°或1440°.
24.(10分)发现:两个差为2的正整数的积与1的和总是一个正整数的平方.
验证:(1)9×7+1是几的平方?
(2)设较小的一个正整数为n,写出这两个正整数积与1的和,并说明它是一个正整数的平方.
延伸:两个差为4的正偶数,它们的积与常数a的和是一个正整数的平方,求a.
【分析】(1)计算9×7+1,即可求解;
(2)设较小的一个正整数为n,那么这两个正整数积与1的和即为(n+2)×n+1,计算即可求解;
延伸解:设较小的正偶数为2k,计算2k(2k+4)+a=4k2+8k+a=,求出a=4.
【解答】解:(1)∵9×7+1=64=82,
∴9×7+1是8的平方;
(2)和为(n+2)×n+1,
∵(n+2)×n+1=n2+2n+1=(n+1)2,
∴原式为正整数(n+1)的平方;
延伸:设较小的正偶数为2k,
∴2k(2k+4)+a=4k2+8k+a=,
由配方法可知a=4,
原式=4(k2+2k+1)=[2(k+1)]2,
综上:a=4.
25.(10分)两个小组攀登一座450m高的山,第二组的攀登速度是第一组的a倍.
(1)若两个小组同时开始攀登,当a=1.2时,第二组比第一组早15min到达顶峰,求两个小组的攀登速度;
(2)元旦假期这两个小组去攀登另一座hm高的山,第二组比第一组晚出发30min,结果两组同时到达顶峰,问第二组的平均攀登速度比第一组快多少?(用含a,h的代数式表示)
【分析】(1)设第一组的速度为xm/min,则第二组的速度为1.2xm/min,根据两个小组同时开始攀登,第二组比第一组早15min,列方程求解.
(2)设第一组的速度为ym/min,则第二组的速度为aym/min,根据两个小组去攀登另一座hm高的山,第二组比第一组晚出发30min,结果两组同时到达顶峰,列方程求解.
【解答】解:(1)设第一组的速度为xm/min,则第二组的速度为1.2xm/min,
由题意得,﹣=15,
解得:x=5,
经检验:x=5是原分式方程的解,且符合题意,
则1.2x=6.
答:第一组的攀登速度5m/min,第二组的攀登速度6m/min;
(2)设第一组的平均速度为ym/min,则第二组的平均速度为aym/min,
由题意得,﹣=30,
解得:y=,
经检验:y=是原分式方程的解,且符合题意,
则ay﹣y=﹣=,
答:第二组的平均攀登速度比第一组快m/min.
26.(12分)如图1,△ABC和△ABD中,∠BAC=∠ABD=90°,点C和点D在AB的异侧,点E为AD边上的一点,且AC=AE,连接CE交直线AB于点G,过点A作AF⊥AD交直线CE于点F.
(Ⅰ)求证:△AGE≌△AFC;
(Ⅱ)若AB=AC,求证:AD=AF+BD;
(Ⅲ)如图2,若AB=AC,点C和点D在AB的同侧,题目其他条件不变,直接写出线段AD,AF,BD的数量关系 AF=AD+BD .
【分析】(Ⅰ)先判断出∠ACF=∠AEG,再用同角的余角相等判断出∠CAF=∠EAG,即可得出结论;
(Ⅱ)先用ASA判断出△ACM≌△ABD,得出AM=AD,CM=BD,由(Ⅰ)知,△AGE≌△AFC,得出∠AGE=∠AFC,再判断出CM∥AB,得出∠MCF=∠AGC,进而判断出MF=CM,即可得出结论;
(Ⅲ)同(Ⅱ)的方法,即可得出结论.
【解答】解:(Ⅰ)∵AC=AE,
∴∠ACF=∠AEG,
∵AF⊥AD,
∴∠DAF=90°=∠CAB,
∴∠DAF﹣∠FAG=∠CAB﹣∠FAG,
∴∠CAF=∠EAG,
在△AGE和△AFC中,
,
∴△AGE≌△AFC(ASA);
(Ⅱ)如图1,
过点C作CM⊥AC,交AF延长线于点M,
∴∠ACM=90°=∠ABD,
由(Ⅰ)知,∠CAF=∠EAB,
在△ACM和△ABD中,
,
∴△ACM≌△ABD(ASA),
∴AM=AD,CM=BD,
由(Ⅰ)知,△AGE≌△AFC,
∴∠AGE=∠AFC,
∴180°﹣∠AGE=180°﹣∠AFC,
∴∠AGC=∠AFG,
∵∠CFM=∠AFG,
∴∠AGC=∠CFM,
∵∠BAC=90°=∠ACM,
∴∠BAC+∠ACM=180°,
∴CM∥AB,
∴∠MCF=∠AGC,
∴∠CFM=∠MCF,
∴MF=CM,
∴AM=AF+CM,
∴AD=AF+BD;
(Ⅲ)AD=AF﹣BD;
过点C作CM⊥AC,交AF于点M,
∴∠ACM=90°=∠ABD,
由(Ⅰ)知,∠CAF=∠EAB,
在△ACM和△ABD中,
,
∴△ACM≌△ABD(ASA),
∴AM=AD,CM=BD,
由(Ⅰ)知,△AGE≌△AFC,
∴∠G=∠F,
∵∠BAC=90°=∠ACM,
∴CM∥AB,
∴∠MCF=∠G,
∴∠F=∠MCF,
∴MF=CM,
∴AF=AM+CM=AD+BD,
故答案为:AF=AD+BD.
同课章节目录
