北师大版九年级下册数学第三章《圆》章末提升训练(二)(Word版 含解析)
文档属性
| 名称 | 北师大版九年级下册数学第三章《圆》章末提升训练(二)(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 199.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-12 00:27:52 | ||
图片预览




文档简介
第三章《圆》章末提升训练(二)
一.选择题
1.在圆内接四边形ABCD中,若∠A=50°,则∠C=( )°
A.40
B.50
C.130
D.150
2.若⊙O的半径为4cm,点A到圆心O的距离为5cm,那么点A与⊙O的位置关系是( )
A.点A在圆外
B.点A在圆上
C.点A在圆内
D.不能确定
3.边长为6的正三角形的外接圆的周长为( )
A.π
B.2π
C.3π
D.4π
4.如图,A,B,C是⊙O上的三个点,∠AOC=63°,∠BCA=25°,则∠BOC的度数为( )
A.100°
B.110°
C.113°
D.120°
5.如图,AB是⊙O的弦,半径OC⊥AB于点D,若⊙O的半径为10cm,AB=16cm,则CD的长是( )
A.2cm
B.3cm
C.4cm
D.5cm
6.如图,AB为半圆O的直径,C是的中点,D是的中点,在上取一点M,上取一点N,使得∠AMN=110°,则下列说法正确的是( )
A.点N在上,且NC>ND
B.点N在上,且NC<ND
C.点N在上,且ND>NB
D.点N在上,且ND<NB
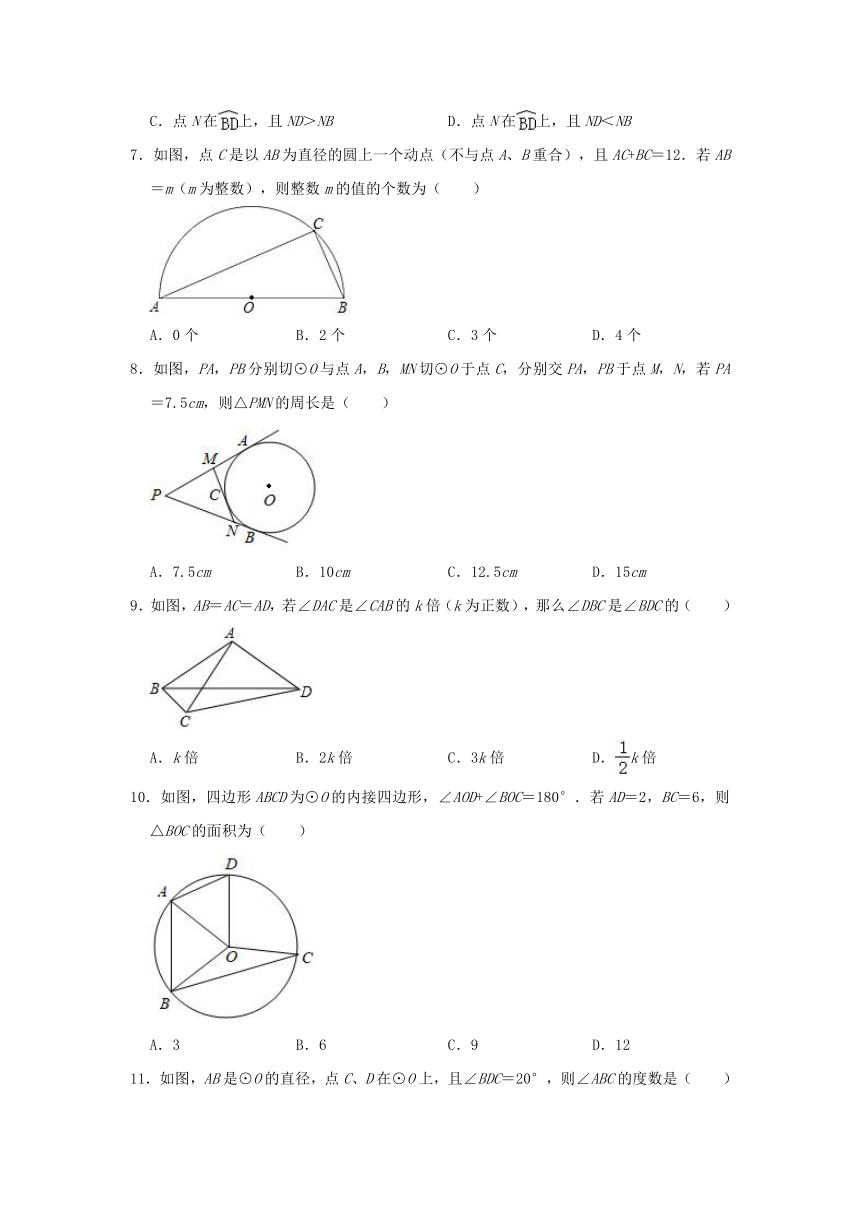
7.如图,点C是以AB为直径的圆上一个动点(不与点A、B重合),且AC+BC=12.若AB=m(m为整数),则整数m的值的个数为( )
A.0个
B.2个
C.3个
D.4个
8.如图,PA,PB分别切⊙O与点A,B,MN切⊙O于点C,分别交PA,PB于点M,N,若PA=7.5cm,则△PMN的周长是( )
A.7.5cm
B.10cm
C.12.5cm
D.15cm
9.如图,AB=AC=AD,若∠DAC是∠CAB的k倍(k为正数),那么∠DBC是∠BDC的( )
A.k倍
B.2k倍
C.3k倍
D.k倍
10.如图,四边形ABCD为⊙O的内接四边形,∠AOD+∠BOC=180°.若AD=2,BC=6,则△BOC的面积为( )
A.3
B.6
C.9
D.12
11.如图,AB是⊙O的直径,点C、D在⊙O上,且∠BDC=20°,则∠ABC的度数是( )
A.20°
B.50°
C.70°
D.80°
12.如图,A是⊙B上任意一点,点C在⊙B外,已知AB=2,BC=4,△ACD是等边三角形,则△BCD的面积的最大值为( )
A.4+4
B.4
C.4+8
D.6
二.填空题
13.正四边形的边长为4,则它的边心距是
.
14.如图,⊙P与y轴相切于点C(0,3),与x轴相交于点A(1,0),B(7,0),直线y=kx﹣1恰好平分⊙P的面积,那么k的值是
.
15.如图,BC是⊙O的弦,以BC为边作等边三角形ABC,圆心O在△ABC的内部,若BC=6,OA=,则⊙O的半径为
.
16.把光盘、含60°角的三角板和直尺如图摆放,AB=2,则光盘的直径是
.
17.如图,以△ABC的边AB为直径的⊙O恰好过BC的中点D,过点D作DE⊥AC于E,连结OD,则下列结论中:①OD∥AC;②∠B=∠C;③2OA=AC;④DE是⊙O的切线;⑤∠EDA=∠B,正确的序号是
.
三.解答题
18.如图,四边形ABDC内接于⊙O,∠BAC=60°,AD平分∠BAC交⊙O于点D,连接OB,OC,BD,CD.
(1)求证:四边形OBDC是菱形;
(2)若∠ABO=15°,OB=2,求弦AC长.
19.如图,已知AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上,连接OA、DE、BE.
(1)若∠AOD=60°,求∠DEB的度数;
(2)若CD=2,弦AB=8,求⊙O的半径长.
20.如图,AB是半圆O的直径,C,D是半圆O上不同于A,B的两点,AC平分∠DAB,AC与BD相交于点F,延长AC到点E,使CE=CF.
(1)求证:BE是半圆O所在圆的切线;
(2)若BC=AD=6,求⊙O的半径.
21.如图,△ABC内接于以AB为直径的⊙O中,且点E是△ABC的内心,AE的延长线与BC交于点F,与⊙O交于点D,⊙O的切线PD交AB的延长线于点P.
(1)试判断△BDE的形状,并给予证明;
(2)若∠APD=30°,BE=2,求AE的长.
参考答案
一.选择题
1.解:∵四边形ABCD是圆内接四边形,
∴∠A+∠C=180°,
∴∠C=180°﹣50°=130°,
故选:C.
2.解:∵⊙O的半径为4cm,点A到圆心O的距离为5cm,5cm>4cm,
∴点A在圆外.
故选:A.
3.解:如图,⊙O为等边△ABC的外接圆,
作OD⊥BC于D,连接OB、OC,
∵△ABC为等边三角形,
∴∠A=60°,
∴∠BOC=120°,
∴∠OBD=30°,
∵OD⊥BC,
∴BD=CD=3,
在Rt△OBD中,OD=BD=,
∴OB=2OD=2,
∴⊙O的周长=2π×2=4π.
故选:D.
4.解:由圆周角定理得,∠AOB=2∠BCA=50°,
∴∠BOC=∠AOC+∠BOA=113°,
故选:C.
5.解:连接OA,则OA=10cm,
∵OC⊥AB,OC过O,AB=16cm,
∴∠ODA=90°,AD=BD=8cm,
在Rt△ODA中,由勾股定理得:OD===6(cm),
∵OC=10cm,
∴CD=OC﹣OD=4cm,
故选:C.
6.解:连接MD,OD、ON、BD,如图,
∵C是的中点,D是的中点,
∴∠BOD=×90°=45°,
∵OB=OD,
∴∠OBD=∠ODB=(180°﹣45°)=67.5°,
∴∠AMD=180°﹣∠ABD=180°﹣67.5°=112.5°,
∵∠AMN=110°,
∴点N在上,
∵∠DMN=∠AMD﹣∠AMN=2.5°,
∴∠DON=2∠DMN=2×2.5°=5°,
∴∠BON=40°,
∴>,
∴BN>DN.
故选:D.
7.解:设AC=x,则BC=12﹣x,
∵点C是以AB为直径的半圆上一个动点(不与点A、B重合),
∴∠ACB=90°,
∴AB2=AC2+BC2,
∴m2=x2+(12﹣x)2,
∴m2=2[(x﹣6)2+36]
∵点C是以AB为直径的半圆上一个动点(不与点A、B重合),
∴0<x<12,
∴0≤(x﹣6)2<36,
∴72≤2[(x﹣6)2+36]<144,
又∵m为整数,
∴当2[(x﹣6)2+36]=81或2[(x﹣4)2+16]=100或2[(x﹣4)2+16]=121时,m为整数9或10或11,
则整数m的值的个数为3个,
故选:C.
8.解:∵直线PA、PB、MN分别与⊙O相切于点A、B、C,
∴MA=MC,NC=NB,
∴△PMN的周长=PM+PN+MC+NC=PM+MA+PN+NB=PA+PB=7.5+7.5=15(cm).
故选:D.
9.解:∵AB=AC=AD,
∴点B、C、D在以A为圆心的圆上,
∴∠BDC=∠CAB,∠DBC=∠DAC,
∵∠DAC=k∠CAB,
∴∠DBC=k∠CAB=k×2∠BDC=k∠BDC,
故选:A.
10.解:延长BO交⊙O于E,连接CE,
则∠COE+∠BOC=180°,∠BCE=90°,
即CE⊥BC,
∵∠AOD+∠BOC=180°,
∴∠AOD=∠COE,
∴=,
∴AD=CE=2,
∵BC=6,
∴△BEC的面积为BC?CE=×6×2=6,
∵OB=OE,
∴△BOC的面积=△BEC的面积=×6=3,
故选:A.
11.解:∵AB是⊙O的直径,
∴∠ACB=90°,
又∵∠A=∠BDC=20°,
∴∠ABC=90°﹣∠A=90°﹣20°=70°,
故选:C.
12.解:以BC为边作等边△BCM,连接DM.
∵∠DCA=∠MCB=60°,
∴∠DCM=∠ACB,
∵DC=AC,MC=BC
∴△DCM≌△CAB(SAS),
∴DM=AB=2为定值,
即点D在以M为圆心,半径为2的圆上运动,
当点D运动至BC的中垂线与圆的交点时,
CB边上的高取最大值为2+2,
此时面积为4+4.
故选:A.
二.填空题(共5小题)
13.解:连接OA,OB,作OE⊥AB于E,如图所示:
∵四边形ABCD是正四边形,
∴∠AOB=360°÷4=90°,
∵OA=OB,
∴△AOB是等腰直角三角形,且OE⊥AB,
∴OE=AB=2,
故答案为:2.
14.解:连接PC,PA,过点P作PD⊥AB于点D,
∵⊙P与y轴相切于点C(0,3),
∴PC⊥y轴,
∴四边形PDOC是矩形,
∴PD=OC=3,
∵A(1,0),B(7,0),
∴AB=7﹣1=6,
∴AD=AB=×6=3,
∴OD=AD+OA=3+1=4,
∴P(4,3),
∵直线y=kx﹣1恰好平分⊙P的面积,
∴3=4k﹣1,解得k=1.
故答案为:1.
15.解:过O作OD⊥BC于D,连接OB,
∵BC是⊙O的一条弦,且BC=6,
∴BD=CD=BC=×6=3,
∴OD垂直平分BC,又AB=AC,
∴点A在BC的垂直平分线上,即A,O及D三点共线,
∵△ABC是等边三角形,
∴∠ABC=60°,
∴AD=BD=3,
∵OA=,
∴OD=AD﹣OA=2
在Rt△OBD中,OB===;
故答案为:.
16.解:设三角板与圆的切点为C,连接OA、OB,如图所示:
由切线长定理知AB=CB=2,OA平分∠ABC,
∴∠OBA=60°,
在Rt△ABO中,OA=ABtan∠OBA=2,
∴光盘的直径为4,
故答案为:4.
17.解:连接AD,
∵D为BC中点,点O为AB的中点,
∴OD为△ABC的中位线,
∴OD∥AC,①正确;
∵AB是⊙O的直径,
∴∠ADB=90°=∠ADC,
即AD⊥BC,又BD=CD,
∴△ABC为等腰三角形,
∴∠B=∠C,②正确;
∵DE⊥AC,且DO∥AC,
∴OD⊥DE,
∵OD是半径,
∴DE是⊙O的切线,∴④正确;
∴∠ODA+∠EDA=90°,
∵∠ADB=∠ADO+∠ODB=90°,
∴∠EDA=∠ODB,
∵OD=OB,
∴∠B=∠ODB,
∴∠EDA=∠B,∴⑤正确;
∵D为BC中点,AD⊥BC,
∴AC=AB,
∵OA=OB=AB,
∴OA=AC,
∴③正确,
故答案为:①②③④⑤.
三.解答题(共4小题)
18.(1)证明:连接OD,
由圆周角定理得,∠BOC=2∠BAC=120°,
∵AD平分∠BAC,
∴,
∴∠BOD=∠COD=60°,
∵OB=OD,OC=OD,
∴△BOD和△COD是等边三角形,
∴OB=BD=DC=OC,
∴四边形OBDC是菱形;
(2)解连接OA,
∵OB=OA,∠ABO=15°,
∴∠AOB=150°,
∴∠AOC=360°﹣150°﹣120°=90°,
∴AC=.
19.解:(1)∵OD⊥AB,
∴=,
∴∠BOD=∠AOD=60°,
∴∠DEB=∠BOD=×60°=30°;
(2)设⊙O的半径为r,则OC=r﹣2,
∵OD⊥AB,
∴AC=BC=AB=×8=4,
在Rt△OAC中,由勾股定理得:(r﹣2)2+42=r2,
解得:r=5,
即⊙O的半径长为5.
20.(1)证明:∵AB是半圆O的直径,
∴∠ACB=∠ADB=90°,
∵CE=CF,
∴BE=BF,
∴∠E=∠BFE,
∵AC平分∠DAB,
∴∠DAF=∠BAF,
∵∠DAF+∠AFD=90°,
∴∠BAF+∠E=90°,
∴BE是半圆O所在圆的切线;
(2)解:∵∠DAF=∠BAF,
∴=,
∵BC=AD,
∴=,
∴==,
∴∠CAB=30°,
∴AB=2BC=12,
∴⊙O的半径为6.
21.解:(1)△BDE为等腰直角三角形,
证明如下:如图,
∵点E是△ABC的内心,
∴BE平分∠ABC,AF平分∠BAC,
∵∠1=∠2,∠3=∠6,
而∠4=∠6,
∴∠2+∠3=∠1+∠4,
而∠5=∠2+∠3,
∴∠5=∠1+∠4,即∠5=∠DBE,
∴DB=DE,
∵AB为直径,
∴∠ADB=90°,
∴△BDE为等腰直角三角形;
(2)连接OD,如图,
∵△BDE为等腰直角三角形,
∴BD=DE=BE=×2=,
∵⊙O的切线PD交AB的延长线于点P,
∴OD⊥PD,
∴∠ODP=90°,
∵∠APD=30°,
∴∠POD=90°﹣∠OPD=60°,
∴∠PAD=∠POD=30°,
在Rt△ABD中,AD=BD=×=,
∴AE=AD﹣DE=﹣.
一.选择题
1.在圆内接四边形ABCD中,若∠A=50°,则∠C=( )°
A.40
B.50
C.130
D.150
2.若⊙O的半径为4cm,点A到圆心O的距离为5cm,那么点A与⊙O的位置关系是( )
A.点A在圆外
B.点A在圆上
C.点A在圆内
D.不能确定
3.边长为6的正三角形的外接圆的周长为( )
A.π
B.2π
C.3π
D.4π
4.如图,A,B,C是⊙O上的三个点,∠AOC=63°,∠BCA=25°,则∠BOC的度数为( )
A.100°
B.110°
C.113°
D.120°
5.如图,AB是⊙O的弦,半径OC⊥AB于点D,若⊙O的半径为10cm,AB=16cm,则CD的长是( )
A.2cm
B.3cm
C.4cm
D.5cm
6.如图,AB为半圆O的直径,C是的中点,D是的中点,在上取一点M,上取一点N,使得∠AMN=110°,则下列说法正确的是( )
A.点N在上,且NC>ND
B.点N在上,且NC<ND
C.点N在上,且ND>NB
D.点N在上,且ND<NB
7.如图,点C是以AB为直径的圆上一个动点(不与点A、B重合),且AC+BC=12.若AB=m(m为整数),则整数m的值的个数为( )
A.0个
B.2个
C.3个
D.4个
8.如图,PA,PB分别切⊙O与点A,B,MN切⊙O于点C,分别交PA,PB于点M,N,若PA=7.5cm,则△PMN的周长是( )
A.7.5cm
B.10cm
C.12.5cm
D.15cm
9.如图,AB=AC=AD,若∠DAC是∠CAB的k倍(k为正数),那么∠DBC是∠BDC的( )
A.k倍
B.2k倍
C.3k倍
D.k倍
10.如图,四边形ABCD为⊙O的内接四边形,∠AOD+∠BOC=180°.若AD=2,BC=6,则△BOC的面积为( )
A.3
B.6
C.9
D.12
11.如图,AB是⊙O的直径,点C、D在⊙O上,且∠BDC=20°,则∠ABC的度数是( )
A.20°
B.50°
C.70°
D.80°
12.如图,A是⊙B上任意一点,点C在⊙B外,已知AB=2,BC=4,△ACD是等边三角形,则△BCD的面积的最大值为( )
A.4+4
B.4
C.4+8
D.6
二.填空题
13.正四边形的边长为4,则它的边心距是
.
14.如图,⊙P与y轴相切于点C(0,3),与x轴相交于点A(1,0),B(7,0),直线y=kx﹣1恰好平分⊙P的面积,那么k的值是
.
15.如图,BC是⊙O的弦,以BC为边作等边三角形ABC,圆心O在△ABC的内部,若BC=6,OA=,则⊙O的半径为
.
16.把光盘、含60°角的三角板和直尺如图摆放,AB=2,则光盘的直径是
.
17.如图,以△ABC的边AB为直径的⊙O恰好过BC的中点D,过点D作DE⊥AC于E,连结OD,则下列结论中:①OD∥AC;②∠B=∠C;③2OA=AC;④DE是⊙O的切线;⑤∠EDA=∠B,正确的序号是
.
三.解答题
18.如图,四边形ABDC内接于⊙O,∠BAC=60°,AD平分∠BAC交⊙O于点D,连接OB,OC,BD,CD.
(1)求证:四边形OBDC是菱形;
(2)若∠ABO=15°,OB=2,求弦AC长.
19.如图,已知AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上,连接OA、DE、BE.
(1)若∠AOD=60°,求∠DEB的度数;
(2)若CD=2,弦AB=8,求⊙O的半径长.
20.如图,AB是半圆O的直径,C,D是半圆O上不同于A,B的两点,AC平分∠DAB,AC与BD相交于点F,延长AC到点E,使CE=CF.
(1)求证:BE是半圆O所在圆的切线;
(2)若BC=AD=6,求⊙O的半径.
21.如图,△ABC内接于以AB为直径的⊙O中,且点E是△ABC的内心,AE的延长线与BC交于点F,与⊙O交于点D,⊙O的切线PD交AB的延长线于点P.
(1)试判断△BDE的形状,并给予证明;
(2)若∠APD=30°,BE=2,求AE的长.
参考答案
一.选择题
1.解:∵四边形ABCD是圆内接四边形,
∴∠A+∠C=180°,
∴∠C=180°﹣50°=130°,
故选:C.
2.解:∵⊙O的半径为4cm,点A到圆心O的距离为5cm,5cm>4cm,
∴点A在圆外.
故选:A.
3.解:如图,⊙O为等边△ABC的外接圆,
作OD⊥BC于D,连接OB、OC,
∵△ABC为等边三角形,
∴∠A=60°,
∴∠BOC=120°,
∴∠OBD=30°,
∵OD⊥BC,
∴BD=CD=3,
在Rt△OBD中,OD=BD=,
∴OB=2OD=2,
∴⊙O的周长=2π×2=4π.
故选:D.
4.解:由圆周角定理得,∠AOB=2∠BCA=50°,
∴∠BOC=∠AOC+∠BOA=113°,
故选:C.
5.解:连接OA,则OA=10cm,
∵OC⊥AB,OC过O,AB=16cm,
∴∠ODA=90°,AD=BD=8cm,
在Rt△ODA中,由勾股定理得:OD===6(cm),
∵OC=10cm,
∴CD=OC﹣OD=4cm,
故选:C.
6.解:连接MD,OD、ON、BD,如图,
∵C是的中点,D是的中点,
∴∠BOD=×90°=45°,
∵OB=OD,
∴∠OBD=∠ODB=(180°﹣45°)=67.5°,
∴∠AMD=180°﹣∠ABD=180°﹣67.5°=112.5°,
∵∠AMN=110°,
∴点N在上,
∵∠DMN=∠AMD﹣∠AMN=2.5°,
∴∠DON=2∠DMN=2×2.5°=5°,
∴∠BON=40°,
∴>,
∴BN>DN.
故选:D.
7.解:设AC=x,则BC=12﹣x,
∵点C是以AB为直径的半圆上一个动点(不与点A、B重合),
∴∠ACB=90°,
∴AB2=AC2+BC2,
∴m2=x2+(12﹣x)2,
∴m2=2[(x﹣6)2+36]
∵点C是以AB为直径的半圆上一个动点(不与点A、B重合),
∴0<x<12,
∴0≤(x﹣6)2<36,
∴72≤2[(x﹣6)2+36]<144,
又∵m为整数,
∴当2[(x﹣6)2+36]=81或2[(x﹣4)2+16]=100或2[(x﹣4)2+16]=121时,m为整数9或10或11,
则整数m的值的个数为3个,
故选:C.
8.解:∵直线PA、PB、MN分别与⊙O相切于点A、B、C,
∴MA=MC,NC=NB,
∴△PMN的周长=PM+PN+MC+NC=PM+MA+PN+NB=PA+PB=7.5+7.5=15(cm).
故选:D.
9.解:∵AB=AC=AD,
∴点B、C、D在以A为圆心的圆上,
∴∠BDC=∠CAB,∠DBC=∠DAC,
∵∠DAC=k∠CAB,
∴∠DBC=k∠CAB=k×2∠BDC=k∠BDC,
故选:A.
10.解:延长BO交⊙O于E,连接CE,
则∠COE+∠BOC=180°,∠BCE=90°,
即CE⊥BC,
∵∠AOD+∠BOC=180°,
∴∠AOD=∠COE,
∴=,
∴AD=CE=2,
∵BC=6,
∴△BEC的面积为BC?CE=×6×2=6,
∵OB=OE,
∴△BOC的面积=△BEC的面积=×6=3,
故选:A.
11.解:∵AB是⊙O的直径,
∴∠ACB=90°,
又∵∠A=∠BDC=20°,
∴∠ABC=90°﹣∠A=90°﹣20°=70°,
故选:C.
12.解:以BC为边作等边△BCM,连接DM.
∵∠DCA=∠MCB=60°,
∴∠DCM=∠ACB,
∵DC=AC,MC=BC
∴△DCM≌△CAB(SAS),
∴DM=AB=2为定值,
即点D在以M为圆心,半径为2的圆上运动,
当点D运动至BC的中垂线与圆的交点时,
CB边上的高取最大值为2+2,
此时面积为4+4.
故选:A.
二.填空题(共5小题)
13.解:连接OA,OB,作OE⊥AB于E,如图所示:
∵四边形ABCD是正四边形,
∴∠AOB=360°÷4=90°,
∵OA=OB,
∴△AOB是等腰直角三角形,且OE⊥AB,
∴OE=AB=2,
故答案为:2.
14.解:连接PC,PA,过点P作PD⊥AB于点D,
∵⊙P与y轴相切于点C(0,3),
∴PC⊥y轴,
∴四边形PDOC是矩形,
∴PD=OC=3,
∵A(1,0),B(7,0),
∴AB=7﹣1=6,
∴AD=AB=×6=3,
∴OD=AD+OA=3+1=4,
∴P(4,3),
∵直线y=kx﹣1恰好平分⊙P的面积,
∴3=4k﹣1,解得k=1.
故答案为:1.
15.解:过O作OD⊥BC于D,连接OB,
∵BC是⊙O的一条弦,且BC=6,
∴BD=CD=BC=×6=3,
∴OD垂直平分BC,又AB=AC,
∴点A在BC的垂直平分线上,即A,O及D三点共线,
∵△ABC是等边三角形,
∴∠ABC=60°,
∴AD=BD=3,
∵OA=,
∴OD=AD﹣OA=2
在Rt△OBD中,OB===;
故答案为:.
16.解:设三角板与圆的切点为C,连接OA、OB,如图所示:
由切线长定理知AB=CB=2,OA平分∠ABC,
∴∠OBA=60°,
在Rt△ABO中,OA=ABtan∠OBA=2,
∴光盘的直径为4,
故答案为:4.
17.解:连接AD,
∵D为BC中点,点O为AB的中点,
∴OD为△ABC的中位线,
∴OD∥AC,①正确;
∵AB是⊙O的直径,
∴∠ADB=90°=∠ADC,
即AD⊥BC,又BD=CD,
∴△ABC为等腰三角形,
∴∠B=∠C,②正确;
∵DE⊥AC,且DO∥AC,
∴OD⊥DE,
∵OD是半径,
∴DE是⊙O的切线,∴④正确;
∴∠ODA+∠EDA=90°,
∵∠ADB=∠ADO+∠ODB=90°,
∴∠EDA=∠ODB,
∵OD=OB,
∴∠B=∠ODB,
∴∠EDA=∠B,∴⑤正确;
∵D为BC中点,AD⊥BC,
∴AC=AB,
∵OA=OB=AB,
∴OA=AC,
∴③正确,
故答案为:①②③④⑤.
三.解答题(共4小题)
18.(1)证明:连接OD,
由圆周角定理得,∠BOC=2∠BAC=120°,
∵AD平分∠BAC,
∴,
∴∠BOD=∠COD=60°,
∵OB=OD,OC=OD,
∴△BOD和△COD是等边三角形,
∴OB=BD=DC=OC,
∴四边形OBDC是菱形;
(2)解连接OA,
∵OB=OA,∠ABO=15°,
∴∠AOB=150°,
∴∠AOC=360°﹣150°﹣120°=90°,
∴AC=.
19.解:(1)∵OD⊥AB,
∴=,
∴∠BOD=∠AOD=60°,
∴∠DEB=∠BOD=×60°=30°;
(2)设⊙O的半径为r,则OC=r﹣2,
∵OD⊥AB,
∴AC=BC=AB=×8=4,
在Rt△OAC中,由勾股定理得:(r﹣2)2+42=r2,
解得:r=5,
即⊙O的半径长为5.
20.(1)证明:∵AB是半圆O的直径,
∴∠ACB=∠ADB=90°,
∵CE=CF,
∴BE=BF,
∴∠E=∠BFE,
∵AC平分∠DAB,
∴∠DAF=∠BAF,
∵∠DAF+∠AFD=90°,
∴∠BAF+∠E=90°,
∴BE是半圆O所在圆的切线;
(2)解:∵∠DAF=∠BAF,
∴=,
∵BC=AD,
∴=,
∴==,
∴∠CAB=30°,
∴AB=2BC=12,
∴⊙O的半径为6.
21.解:(1)△BDE为等腰直角三角形,
证明如下:如图,
∵点E是△ABC的内心,
∴BE平分∠ABC,AF平分∠BAC,
∵∠1=∠2,∠3=∠6,
而∠4=∠6,
∴∠2+∠3=∠1+∠4,
而∠5=∠2+∠3,
∴∠5=∠1+∠4,即∠5=∠DBE,
∴DB=DE,
∵AB为直径,
∴∠ADB=90°,
∴△BDE为等腰直角三角形;
(2)连接OD,如图,
∵△BDE为等腰直角三角形,
∴BD=DE=BE=×2=,
∵⊙O的切线PD交AB的延长线于点P,
∴OD⊥PD,
∴∠ODP=90°,
∵∠APD=30°,
∴∠POD=90°﹣∠OPD=60°,
∴∠PAD=∠POD=30°,
在Rt△ABD中,AD=BD=×=,
∴AE=AD﹣DE=﹣.
