【名师课件】苏教版六年级下册数学 第4单元 比例(7课时,118张幻灯片)
文档属性
| 名称 | 【名师课件】苏教版六年级下册数学 第4单元 比例(7课时,118张幻灯片) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-12 09:06:09 | ||
图片预览







文档简介
1、图形的放大与缩小
导入新课
王晓光拖动电脑的鼠标,把一副长方形照片放大。
原来长方形照片长8厘米,宽5厘米;
放大后长方形照片长16厘米,宽10厘米。
探究新知
原图
放大后
仔细观察放大前后,照片的长有什么关系?宽呢?
8厘米
5厘米
16厘米
10厘米
探究新知
原图
{5940675A-B579-460E-94D1-54222C63F5DA}
8
5
16
10
每格表示1厘米
放大后
把长方形的每条边放大到原来的2倍。
放大后的长方形与原来长方形对应边长的比是2∶1。
就是把原来的长方形按2∶1的比放大。
放大后边的长度:放大前边的长度
2 ∶1
探究新知
把长方形的长和宽都放大到原来的3倍,放大后的长方形和原来长方形对应边长的比是( ),这就是把原来的长方形按( )的比放大。
3 : 1
3 : 1
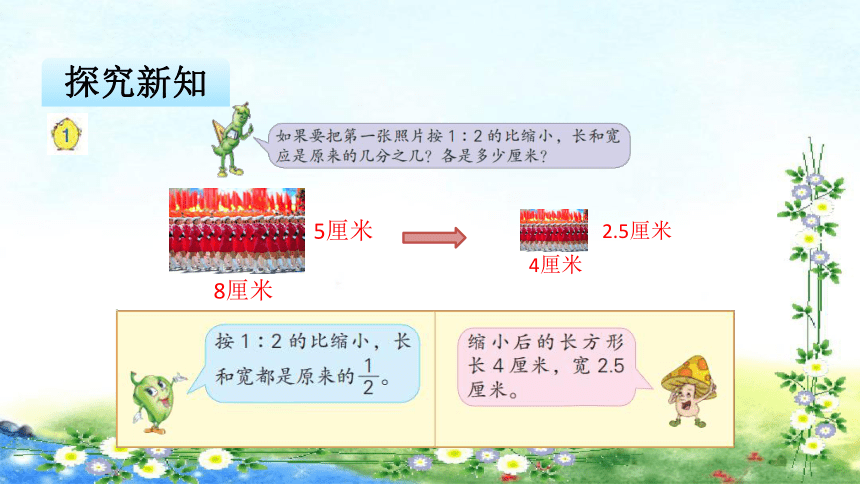
探究新知
8厘米
5厘米
4厘米
2.5厘米
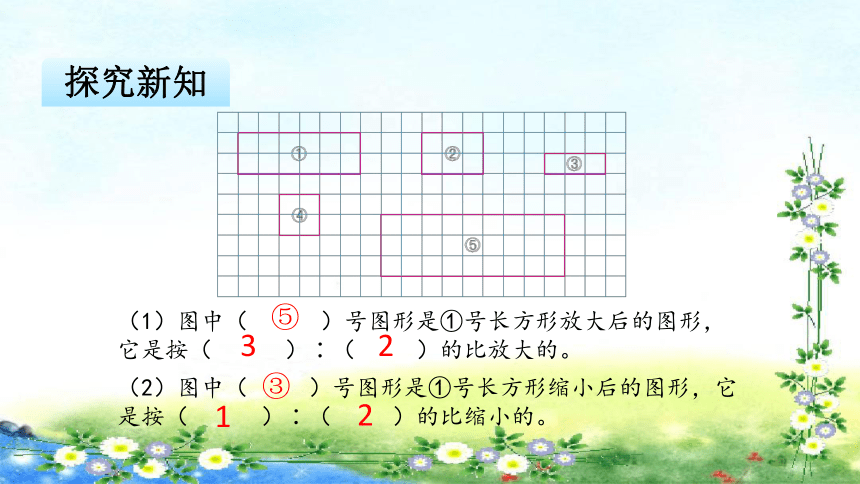
探究新知
(1)图中( )号图形是①号长方形放大后的图形, 它是按( )∶( )的比放大的。
(2)图中( )号图形是①号长方形缩小后的图形,它是按( )∶( )的比缩小的。
⑤
③
3
2
1
2
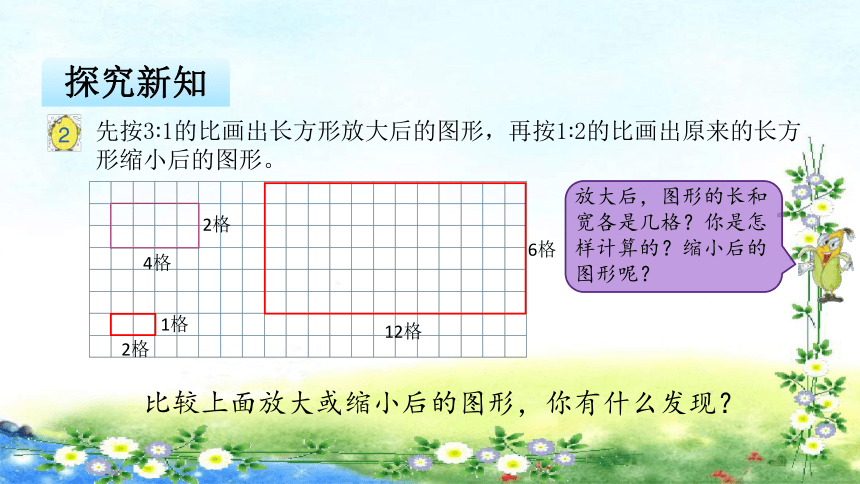
探究新知
先按3?1的比画出长方形放大后的图形,再按1?2的比画出原来的长方形缩小后的图形。
放大后,图形的长和宽各是几格?你是怎样计算的?缩小后的图形呢?
4格
2格
12格
6格
2格
1格
比较上面放大或缩小后的图形,你有什么发现?
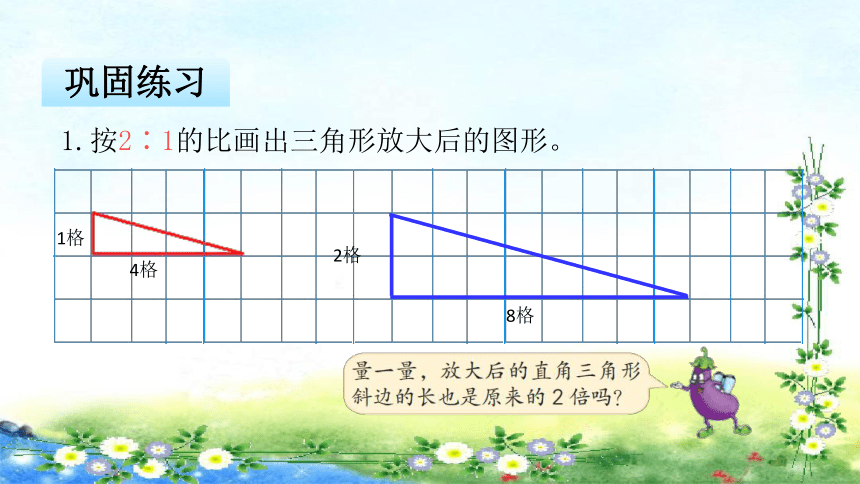
巩固练习
1.按2∶1的比画出三角形放大后的图形。
4格
1格
8格
2格
巩固练习
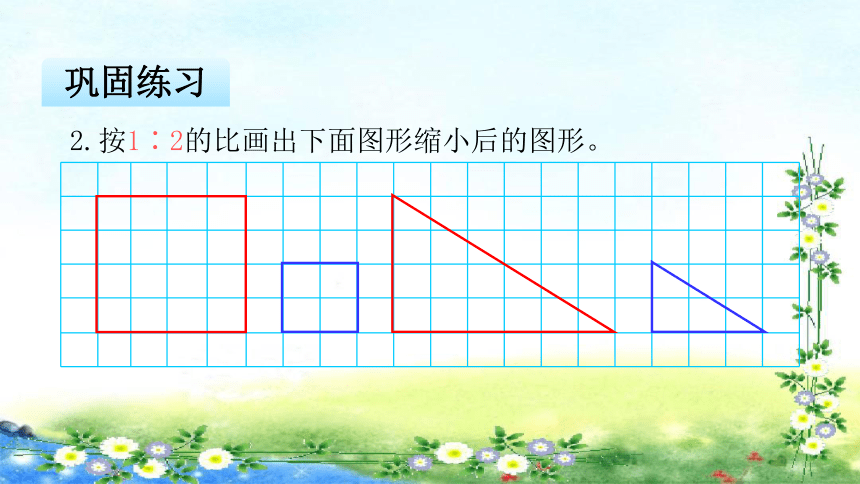
2.按1∶2的比画出下面图形缩小后的图形。
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
巩固练习
3.按2:1的比画出正方形放大后的图形,再按1:2的比画出长方形缩小后的图形。
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
拓展练习
4.一个三角形的底是4 cm,高是6 cm,如果将它按3:1放大,求放大后图形的面积。?
4×3=12(厘米)
6×3=18(厘米)
12×18÷2
=216÷2
=108(平方厘米)
答:放大后图形的面积是108平方厘米。
课堂总结
图形的放大与缩小
放大(缩小)后图形的比
按比例画出放大(缩小)后的图形
按比例将图形的对应边放大(缩小)
放大后边的长度:放大前边的长度
按比例画出图形
数学阅读
当观察或研究一些非常细微、甚至肉眼不能看清的物体时,如:细菌、人类的神经、血管以及一些细小的零件,人们需要把它按照一定的比进行放大,以便观察研究。
显微镜下的雪花
(按10000∶1的比放大)
数学阅读
同样,在绘制地图、制作航模、车模的时候,又需要把原物按照一定的比缩小。在深圳就有一个世界之窗微缩景观,它就是把一些名胜古迹、世界奇观按照一定的比缩小仿制而成的。
2、比 例 的 意 义
导入新课
一张长方形的照片长6.4厘米,宽4厘米,把它按一定比放大后变成长为9.6厘米,你知道它是按( ):( )的比放大的吗?放大后的宽应是多少?
4×1.5=6(厘米)
9.6:6.4=3:2
它是按3:2的比放大的。
放大后的宽是6厘米。
导入新课
根据放大前后的两张长方形照片,你能写出哪些比?
探究新知
(1)放大前的照片长和宽的比是6.4:4。
(2)放大后的照片长和宽的比9.6:6。
(3)放大后与放大前长的比是9.6:6.4。
(4)放大后与放大前宽的比是6:4。
猜一猜:哪两个比之间可能存在关系?
探究新知
小组讨论:
1.两个比之间存在的关系,并说一说是怎样判断的?
2.可以分别求出它们的比值,或把它们分别化简。
探究新知
6.4:4=9.6:6 或 =
像这样表示两个比相等的式子叫作比例。
巩固练习
1. 哪几组的两个比可以组成比例? 把组成的比例写出来。
(1) 10:12 和 25:30 (2) 2:8 和 9:27
(3) 0.9:3 和 15:115 (4) : 和 :
10:12 = 25:30
巩固练习
2. 商场开展促销活动, 所有商品一律八折优惠。
50 : 40 = 200 : 160 (答案不唯一)
巩固练习
3. 一辆汽车上午 4 小时行驶 320 千米, 下午 3 小时行驶 240 千米。
(1) 上午行驶的路程和时间的比是几比几? 下午呢? 这两个比能组成比例吗? 为什么?
上午行驶的路程和时间的比是320 : 4,下午行驶的路程和时间的比是240 : 3。
这两个比能组成比例,因为320 : 4 = 4: 3。
巩固练习
3. 一辆汽车上午 4 小时行驶 320 千米, 下午 3 小时行驶 240 千米。
(2) 上、 下午行驶路程的比和上、 下午行驶时间的比也能组成比例吗?
320 : 240 = 4 : 3,上、 下午行驶路程的比和上、 下午行驶时间的比能组成比例。
巩固练习
4. 判断下面哪个比能与 : 4 组成比例。
(1) 5:4 (2) 20:1 (3) 1:20 (4) 5:
1 : 20 = : 4
巩固练习
5. 李梅为了布置教室墙报, 剪了三张大小不同的长方形剪纸。
(1)写出每张长方形剪纸长与宽的比,并算出比值。
15:10=3:2=
18:12=3:2=
24:16=3:2=
巩固练习
5. 李梅为了布置教室墙报, 剪了三张大小不同的长方形剪纸。
15 :10 = 18 : 12
(2)选择其中的两个比组成比例。
巩固练习
下面各表中相对应的两个数量的比能否组成比例?如果能组成比例, 把组成的比例写出来。
240:4=360:6
20:5=28:7
2.1:3=3.5:5
不能组成比例
巩固练习
观察下面的两幅图, 左图中的两个长方形有什么关系? 右图中的两个平行四边形呢?
左图中的小长方形按比例放大得到大长方形, 右图中的小平行四边形按比例放大得到大平行四边形。
巩固练习
你能照样子分别把下面的三角形和四边形按 2:1 的比放大吗?
拓展练习
1. 从12的因数中任意选出4个数,组成两个比例。
( 1 ):( 2 )=( 3 ):( 6 )
12的因数:1、2、3、4、6、12
( 2 ):( 3 )=( 4 ):( 6 )
……
拓展练习
2. 某日上午,阳光下人高1.5米,影长1.2米;树高3.5米,影长2.8米。分别求出人高和影长的比、树高和影长的比。它们能组成比例吗?
人高:影长=1.5:1.2=
人高:影长=树高:影长 1.5:1.2=3.5:2.8
树高:影长=3.5:2.8=
比值相等,所以能组成比例。
课堂总结
表示两个比相等的式子叫作比例。
数学阅读
阿基米德有许多故事,其中最着名的要算发现阿基米德定律的那个洗澡的故事了。
国王做了一顶金王冠,他怀疑工匠用银子偷换了一部分金子,便要阿基米德鉴定它是不是纯金制的,且不能损坏王冠。阿基米德捧着这顶王冠整天苦苦思索,有一天,阿基米德去浴室洗澡,他跨入浴桶,随着身子浸入浴桶,一部分水就从桶边溢出,阿基米德看到这个现象,头脑中像闪过一道闪电,“我找到了!”他兴奋地大喊道。
数学阅读
阿基米德拿一块金块和一块质量相等的银块,分别放入一个盛满水的容器中,发现银块排出的水多得多。于是阿基米德拿了与王冠质量相等的金块,放入盛满水的容器里,测出排出的水量;再把王冠放入盛满水的容器里,看看排出的水量是否一样,问题就解决了。随着进一步研究,沿用至今的流体力学最重要基石——阿基米德定律诞生了。
3、比例的基本性质
导入新课
什么叫作比例?
什么样的两个比才能组成比例?
探究新知
把左边的三角形按比例缩小后得到的右边的三角形。
你能根据图中数据写出不同的比例吗?
每个三角形底的和高的比相等。
6 : 4= 3 : 2
两个三角形高的比和底的比相等。
4 : 2= 6 : 3
两个三角形底的比和高的比相等。
6 : 3 = 4 : 2
每个三角形的高和底的比相等。
4 : 6= 2 : 3
组成比例的四个数,叫作比例的项。
两端的两项叫作比例的外项,
中间的两项叫作比例的内项。
例如:6 : 3 = 4 : 2
其他三个比例的内项和外项各是多少?
4 : 2 = 6 : 3
6 : 4 = 3 : 2
4 : 6 = 2 : 3
观察上面的四个比例, 你有什么发现?
再写出一些比例, 看看是不是有同样的规律。
6 和 2 可以同时是比
例的外项, 也可以
同时是比例的内项。
3 和 4 可以同时是比
例的内项 , 也可以
同时是比例的外项。
6 × 2 = 3 × 4,
两个外项的积与两
个内项的积相等。
如果用字母表示比例的四个项, 即 a:b = c:d, 那么这个规律可以表示成:
a × d = b × c
在比例里,两个外项的积等于两个内项的积, 这叫作比例的基本性质。
如果把比例写成分数形式,把等号两端的分子、 分母交叉相乘, 结果怎样?
6 × 2 = 3 × 4
巩固练习
应用比例的基本性质,判断下面每组的两个比能否组成比例。
如果能组成比例,把组成的比例写出来。
3.6:1.8 和 0.5:0.25
和 18:24
3.6×0.25=0.9
1.8×0.5=0.9
3.6×0.25=1.8×0.5
所以3.6:1.8=0.5:0.25
×18= ×24
所以 = 18:24
×24=6
×18=6
拓展练习
1. 一列火车从甲城开往乙城, 行驶速度和所需时间如下表:
(1) 从表中选择两组数据,写出一个乘积相等的式子。
(2) 根据上面的等式,写出一个比例。
6 × 80 = 4 × 120
4 : 6 = 80 : 120
拓展练习
2. 根据比例的基本性质, 在括号里填上合适的数。
( ): 6 = 4 : ( )
5 :( )=( ): 8
3
8
10
4
课堂总结
比例的基本性质:
比例
各部分名称
项
外项
内项
两个外项的积等于两个内项的积
数学阅读
黄金分割又称黄金律,是指事物各部分间一定的数学比例关系,即将整体一分为二,较大部分与整体部分的比值等于较小部分与较大部分的比值,其比值约为0.618。
4、解比例
导入新课
1.解下列简易方程,并口述过程。
x÷4=1.8 3(X+2)=18
2.什么叫作比例?比例有什么基本性质?
3.应用比例的基本性质,判断下面哪一组中的两个
比可以组成比例?
6:10和9:15 20:5和4:1 5:1和6:2
探究新知
探究新知
根据题意写出长与宽的比相等的比例,因为放大后照片的宽是未知的,可以用x表示,我们设未知量宽是x厘米,然后按长和宽的比写出比例。
探究新知
巩固练习
巩固练习
巩固练习
巩固练习
巩固练习
巩固练习
巩固练习
巩固练习
拓展练习
课堂总结
解比例
应用比例基本性质求未知数
数学阅读
泰勒斯来到埃及,人们想试探一下他的能力,就问他是否能测量金字塔高度。泰勒斯说可以,但有一个条件——法老必须在场。第二天,法老如约而至,金字塔周围也聚集了不少围观的老百姓。泰勒斯来到金字塔前,阳光把他的影子投在地面上。每过一会儿,他就让人测量他影子的长度,当测量值与他身高完全吻合时,他立刻在大金字塔在地面上的投影处作一记号,然后在丈量金字塔底到投影顶尖的距离。这样,他就报出了金字塔确切的高度。
5、比例尺
导入新课
中国的国土面积大约有960万平方千米。但是我们却能在一张不大的纸上把它画下来,你知道这是为什么吗?
探究新知
红光小学有一块长方形草坪,长50米,宽30米。把这块草坪按一定的比例缩小,画出的平面图长5厘米,宽3厘米。你能分别写出草坪长、宽的图上距离和实际距离的比吗?
图上距离
实际距离
5厘米怎么和50米比呢?
探究新知
5厘米怎么和50米比呢?
图上距离和实际距离的单位不同,先要把它们统一成相同的单位,写出比后再化简。
探究新知
50米=5000厘米
5∶5000=1∶1000
草坪长的图上距离和实际距离的比是1∶1000。
30米=3000厘米
3∶3000=1∶1000
草坪宽的图上距离和实际距离的比是1∶1000。
比例尺
探究新知
一幅图的图上距离和实际距离的比,叫作这幅图的比例尺。
图上距离∶实际距离=比例尺
图上距离
实际距离
=比例尺
或
探究新知
红光小学有一块长方形草坪,长50米,宽30米。把这块草坪按一定的比例缩小,画出的平面图长5厘米,宽3厘米。你能分别写出草坪长、宽的图上距离和实际距离的比吗?
这幅平面图的比例尺是多少?
1∶1000
探究新知
你能说说比例尺1∶1000的含义吗?
比例尺1:1000,表示图上距离是实际距离的 。
11000
?
比例尺1:1000,表示实际距离是图上距离的1000倍。
根据比例尺,可以知道图上距离1厘米表示实际距离10米。
探究新知
比例尺1∶1000还可以这样表示:
它表示图上1厘米的距离相当于实际距离10米。
巩固练习
1.说出下面比例尺的实际意义。
图上1厘米表示实际距离22千米。
图上1厘米表示实际距离15千米。
巩固练习
2.荷花村到杏树村的实际距离是15千米。量出这两个村的图上距离,并算出这幅图的比例尺。
3厘米
15千米=1500000厘米
3∶1500000=1∶500000
这幅图的比例尺是1∶500000。
巩固练习
3.解比例。
3????=6×7
?
????=14
?
23????=10×45
?
????=12
?
15????=2.4×5
?
????=60
?
拓展练习
1.上海到杭州的实际距离大约是180千米,在一幅地图上量得两地间的距离是5厘米。求这幅地图的比例尺。
180千米=18000000厘米
5∶18000000=1∶3600000
答:这幅地图的比例尺是1∶3600000。
拓展练习
2.下面是实验小学体育场的平面图。体育场长150米,宽70米。求这幅图的比例尺,并在括号里填上合适的数。
150米=15000厘米
7.5∶15000=1∶2000
答:这幅图的比例尺是1∶2000。
20
40
60
拓展练习
3.下面是小青从家到梅花山的路线图。
(1)小青家到梅花山的路程大约是多少千米?
图中线段长10.5厘米。
10.5×400=4200(米)
答:小青家到梅花山的路程大约是4.2千米。
4200米=4.2千米
拓展练习
3.下面是小青从家到梅花山的路线图。
(2)小青早上8∶00从家出发,以12千米/时的速度骑自行车去梅花山,需要多少分钟到达?
4.2÷12=0.35(时)
0.35时=21分
答:需要21分钟到达。
课堂总结
比例尺
比例尺的含义
一幅图的图上距离和实际距离的比
表示方法
图上距离∶实际距离=比例尺
图上距离
实际距离
=比例尺
用线段比例尺表示
数学阅读
按照国家规定的标准、图示和比例尺绘制的地图叫作国家基本比例尺地图。我国的国家基本比例尺地图的比例尺有以下11种:
1 ∶500、1 ∶1000、1 ∶2000、1 ∶5000、1 ∶10000、1 ∶25000、1 ∶50000、1 ∶100000、1 ∶200000、1 ∶500000、1 ∶1000000。
6、比例尺的应用
复习导入
求比例尺的方法是:
第一种方法:图上距离:实际距离
第二种方法:
图上距离
实际距离
=比例尺
=比例尺
探究新知
探究新知
(1)图上1厘米的线段表示实际距离8000厘米;
(2)实际距离是图上距离的8000倍;
(3)图上距离是实际距离的 。
8000
1
探究新知
比例尺1:8000
方法一
方法二
方法三
5×8000=40000(厘米) 40000厘米=400米
8000厘米=80米 80×5=400(米)
5
=40000(厘米)
÷
8000
1
探究新知
解:设明华小学到少年宫的实际距离是χ厘米。
5
χ
=
1
8000
40000厘米=400米
方法五
答:明华小学到少年宫的实际距离是400米。
χ= 5×8000
χ= 40000
医院在明华小学的正北方向,它们之间的实际距离是240米。先算出明华小学到医院的图上距离,再在上图中表示出医院的位置。
探究新知
方法二:8000厘米=80米
240÷80=3(厘米)
比例尺1:8000
探究新知
24000 × =3(厘米)
8000
1
240米=24000厘米
方法一:
·
医院
3厘米
下面是梅镇汽车站附近的平面图。
.
.
.
镇政府
汽车站
敬老院
北
巩固练习
比例尺1:20000
(1)分别量出汽车站到镇政府和敬老院的图上距离,再算出实际距离各是多少米。
巩固练习
.
.
.
镇政府
汽车站
敬老院
3 cm
3.5 cm
汽车站到镇政府的实际距离为:
3×20000=60000(厘米)
比例尺1:20000
60000厘米=600米
汽车站到敬老院的实际距离为:3.5×20000=70000(厘米)
70000厘米=700米
北
.
镇政府
比例尺1 : 20000
·
20000厘米=200米
400÷200=2(cm)
.
.
汽车站
敬老院
北
幼儿园
2厘米
(2)幼儿园在汽车站的正西方向400米处,你能在图中表示出幼儿园的位置吗?
“神州”九号载人飞船返回舱着陆在内蒙古的四子王旗。在比例尺是1:15000000的地图上,量得四子王旗与北京的距离是3厘米。两地间的实际距离大约是多少千米?
3×15000000=45000000(厘米)
45000000厘米=450千米
答:两地间的实际距离大约是450千米。
拓展练习
·
街心花园
北
桃林小学在街心花园正东方向650米处,大众超市在桃林小学正北方向200米处。在图中表示出桃林小学和大众超市的位置。
·
桃林小学
·
大众超市
650÷100=6.5(厘米)
200÷100=2(厘米)
1:16000
1400 m
15 cm
3000000厘米=30千米 450÷30=15(厘米)
800米=80000厘米 5:80000=1:16000
3.5×40000=140000(厘米) 140000厘米=1400米
7.下面是小青从家到梅花山的路线图。
(1)小青家到梅花山的路程大约是多少千米?
5+3+2.5=10.5(厘米)
400×10.5=4200(米)
4200米=4.2千米
答:小青家到梅花山的路程大约是4.2千米。
(2)小青早上8:00从家出发,以12千米/时的速度骑自行车去梅花山,需要多少分钟到达?
4.2÷12×60=21(分)
答:需要21分钟到达。
8.找一幅中国地图,量出上海到北京的图上距离,并根据地图的比例尺计算实际距离大约是多少千米。
比例尺1:9000000
12 cm
108000000厘米=1080千米
比例尺1:9000000
图上距离:12厘米
实际距离:9000000×12=108000000(厘米)
答:上海到北京的实际距离大约是1080千米 。
课堂总结
不管是求图上距离还是实际距离,都要弄清题里的条件和问题,再根据“图上距离:实际距离=比例尺”这个关系式列方程,在用实际距离和比例尺求图上距离时,先要把实际距离和图上距离的单位统一,再列方程;在用图上距离和比例尺求实际问题时,求出的实际距离能化成米或千米作单位的数时要化成米或千米作单位的数。
7、面积的变化
导入新课
判断:一幅地图的比例尺是1:1000,那么图上面积与实际面积的比也是1:1000。
提问:这句话对吗?你能说说你的理由吗?
一个长方形的长和宽按比例放大后,面积会按照怎样的规律发生变化呢?
探究新知
下面的大长方形是小长方形按比例放大后得到的。分别量出它们的长和宽,写出对应边长的比。
大长方形与小长方形的长的比是( ):( ),宽的比是( ):( )
3
1
3
1
探究新知
估计一下大长方形和小长方形的面积比是几比几,再算一算,看看你估计的对不对。
怎么验证的?
验证方法:
(1)计算出面积说明。
(2)在大长方形中画小长方形。
探究新知
放大的长方形和原来相比,对应边长度的比是3:1,可是,面积的比却不一样,变成了9:1。你得到了什么结论?
如果大长方形与小长方形对应边的比是4:1,那么面积比是几比几呢?
面积比是16:1。
探究新知
其他平面图形按比例放大后,面积的比又会怎样变化呢?
探究新知
正方形 3:1
三角形 2:1
圆 4:1
估计一下,它们的对应边是按几比几的比放大的?
测量一下,它们的对应边是按几比几的比放大的?
探究新知
这几个图形放大后与放大前的面积相比,发生了怎样的变化?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
放大前
放大后
放大后与放大前的比较
正方形
边长/cm
面积/cm?
三角形
底/cm
高/cm
面积/cm?
圆
半径/cm
面积/cm?
1
0.5
3:1
9:1
2:1
2:1
4:1
4:1
16:1
1
1
1
2
0.25
3
9
4
2
4
2
4
探究新知
比较每个图形放大后与放大前的长度比和面积比,你能发现什么?规律?
如果把一个图形按n:1的比放大,放大后与放大前图形的面积比是( ):( )。
n?
1
巩固练习
1.将面积是8平方厘米的长方形按2:1的比例放大后,得到的长方形的面积是( )平方厘米。
32
想:按2:1的比例放大,面积将扩大到原来的2?=4倍,8×4=32(平方厘米)。
巩固练习
因为放大后与放大前的面积的比是9:1,所以对应高的比是3:1。
解:设放大前的高是x分米。
6:x=3:1
x=2
答:放大前的高是2分米。
2.把一个三角形按一定的比例放大,它们的面积比是9:1,放大后的三角形的高是6分米,放大前的三角形的高是多少?
巩固练习
在第112页的方格纸上画一个平行四边形,按比例放大,算一算放大后与放大前图形的面积比,看看是不是符合上面发现的规律。
如果把一个平面图形按指定的某个比缩小,缩小前后图形面积的变化规律又是什么呢?
拓展练习
一个长方体、正方体或圆柱体按比例放大,如果放大后与放大前图形的对应边长度的比是n:1,那么放大后与放大前图形体积的比是( )。
n?: 1
课堂总结
回顾探索规律的过程,你有什么收获?还想到了什么?
寻找面积的变化规律,要对放大前后的图形进行比较。
认真观察比较数据,才能发现规律。
长方体、正方体按比例放大后,体积比和长度比会有什么关系?
导入新课
王晓光拖动电脑的鼠标,把一副长方形照片放大。
原来长方形照片长8厘米,宽5厘米;
放大后长方形照片长16厘米,宽10厘米。
探究新知
原图
放大后
仔细观察放大前后,照片的长有什么关系?宽呢?
8厘米
5厘米
16厘米
10厘米
探究新知
原图
{5940675A-B579-460E-94D1-54222C63F5DA}
8
5
16
10
每格表示1厘米
放大后
把长方形的每条边放大到原来的2倍。
放大后的长方形与原来长方形对应边长的比是2∶1。
就是把原来的长方形按2∶1的比放大。
放大后边的长度:放大前边的长度
2 ∶1
探究新知
把长方形的长和宽都放大到原来的3倍,放大后的长方形和原来长方形对应边长的比是( ),这就是把原来的长方形按( )的比放大。
3 : 1
3 : 1
探究新知
8厘米
5厘米
4厘米
2.5厘米
探究新知
(1)图中( )号图形是①号长方形放大后的图形, 它是按( )∶( )的比放大的。
(2)图中( )号图形是①号长方形缩小后的图形,它是按( )∶( )的比缩小的。
⑤
③
3
2
1
2
探究新知
先按3?1的比画出长方形放大后的图形,再按1?2的比画出原来的长方形缩小后的图形。
放大后,图形的长和宽各是几格?你是怎样计算的?缩小后的图形呢?
4格
2格
12格
6格
2格
1格
比较上面放大或缩小后的图形,你有什么发现?
巩固练习
1.按2∶1的比画出三角形放大后的图形。
4格
1格
8格
2格
巩固练习
2.按1∶2的比画出下面图形缩小后的图形。
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
巩固练习
3.按2:1的比画出正方形放大后的图形,再按1:2的比画出长方形缩小后的图形。
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
拓展练习
4.一个三角形的底是4 cm,高是6 cm,如果将它按3:1放大,求放大后图形的面积。?
4×3=12(厘米)
6×3=18(厘米)
12×18÷2
=216÷2
=108(平方厘米)
答:放大后图形的面积是108平方厘米。
课堂总结
图形的放大与缩小
放大(缩小)后图形的比
按比例画出放大(缩小)后的图形
按比例将图形的对应边放大(缩小)
放大后边的长度:放大前边的长度
按比例画出图形
数学阅读
当观察或研究一些非常细微、甚至肉眼不能看清的物体时,如:细菌、人类的神经、血管以及一些细小的零件,人们需要把它按照一定的比进行放大,以便观察研究。
显微镜下的雪花
(按10000∶1的比放大)
数学阅读
同样,在绘制地图、制作航模、车模的时候,又需要把原物按照一定的比缩小。在深圳就有一个世界之窗微缩景观,它就是把一些名胜古迹、世界奇观按照一定的比缩小仿制而成的。
2、比 例 的 意 义
导入新课
一张长方形的照片长6.4厘米,宽4厘米,把它按一定比放大后变成长为9.6厘米,你知道它是按( ):( )的比放大的吗?放大后的宽应是多少?
4×1.5=6(厘米)
9.6:6.4=3:2
它是按3:2的比放大的。
放大后的宽是6厘米。
导入新课
根据放大前后的两张长方形照片,你能写出哪些比?
探究新知
(1)放大前的照片长和宽的比是6.4:4。
(2)放大后的照片长和宽的比9.6:6。
(3)放大后与放大前长的比是9.6:6.4。
(4)放大后与放大前宽的比是6:4。
猜一猜:哪两个比之间可能存在关系?
探究新知
小组讨论:
1.两个比之间存在的关系,并说一说是怎样判断的?
2.可以分别求出它们的比值,或把它们分别化简。
探究新知
6.4:4=9.6:6 或 =
像这样表示两个比相等的式子叫作比例。
巩固练习
1. 哪几组的两个比可以组成比例? 把组成的比例写出来。
(1) 10:12 和 25:30 (2) 2:8 和 9:27
(3) 0.9:3 和 15:115 (4) : 和 :
10:12 = 25:30
巩固练习
2. 商场开展促销活动, 所有商品一律八折优惠。
50 : 40 = 200 : 160 (答案不唯一)
巩固练习
3. 一辆汽车上午 4 小时行驶 320 千米, 下午 3 小时行驶 240 千米。
(1) 上午行驶的路程和时间的比是几比几? 下午呢? 这两个比能组成比例吗? 为什么?
上午行驶的路程和时间的比是320 : 4,下午行驶的路程和时间的比是240 : 3。
这两个比能组成比例,因为320 : 4 = 4: 3。
巩固练习
3. 一辆汽车上午 4 小时行驶 320 千米, 下午 3 小时行驶 240 千米。
(2) 上、 下午行驶路程的比和上、 下午行驶时间的比也能组成比例吗?
320 : 240 = 4 : 3,上、 下午行驶路程的比和上、 下午行驶时间的比能组成比例。
巩固练习
4. 判断下面哪个比能与 : 4 组成比例。
(1) 5:4 (2) 20:1 (3) 1:20 (4) 5:
1 : 20 = : 4
巩固练习
5. 李梅为了布置教室墙报, 剪了三张大小不同的长方形剪纸。
(1)写出每张长方形剪纸长与宽的比,并算出比值。
15:10=3:2=
18:12=3:2=
24:16=3:2=
巩固练习
5. 李梅为了布置教室墙报, 剪了三张大小不同的长方形剪纸。
15 :10 = 18 : 12
(2)选择其中的两个比组成比例。
巩固练习
下面各表中相对应的两个数量的比能否组成比例?如果能组成比例, 把组成的比例写出来。
240:4=360:6
20:5=28:7
2.1:3=3.5:5
不能组成比例
巩固练习
观察下面的两幅图, 左图中的两个长方形有什么关系? 右图中的两个平行四边形呢?
左图中的小长方形按比例放大得到大长方形, 右图中的小平行四边形按比例放大得到大平行四边形。
巩固练习
你能照样子分别把下面的三角形和四边形按 2:1 的比放大吗?
拓展练习
1. 从12的因数中任意选出4个数,组成两个比例。
( 1 ):( 2 )=( 3 ):( 6 )
12的因数:1、2、3、4、6、12
( 2 ):( 3 )=( 4 ):( 6 )
……
拓展练习
2. 某日上午,阳光下人高1.5米,影长1.2米;树高3.5米,影长2.8米。分别求出人高和影长的比、树高和影长的比。它们能组成比例吗?
人高:影长=1.5:1.2=
人高:影长=树高:影长 1.5:1.2=3.5:2.8
树高:影长=3.5:2.8=
比值相等,所以能组成比例。
课堂总结
表示两个比相等的式子叫作比例。
数学阅读
阿基米德有许多故事,其中最着名的要算发现阿基米德定律的那个洗澡的故事了。
国王做了一顶金王冠,他怀疑工匠用银子偷换了一部分金子,便要阿基米德鉴定它是不是纯金制的,且不能损坏王冠。阿基米德捧着这顶王冠整天苦苦思索,有一天,阿基米德去浴室洗澡,他跨入浴桶,随着身子浸入浴桶,一部分水就从桶边溢出,阿基米德看到这个现象,头脑中像闪过一道闪电,“我找到了!”他兴奋地大喊道。
数学阅读
阿基米德拿一块金块和一块质量相等的银块,分别放入一个盛满水的容器中,发现银块排出的水多得多。于是阿基米德拿了与王冠质量相等的金块,放入盛满水的容器里,测出排出的水量;再把王冠放入盛满水的容器里,看看排出的水量是否一样,问题就解决了。随着进一步研究,沿用至今的流体力学最重要基石——阿基米德定律诞生了。
3、比例的基本性质
导入新课
什么叫作比例?
什么样的两个比才能组成比例?
探究新知
把左边的三角形按比例缩小后得到的右边的三角形。
你能根据图中数据写出不同的比例吗?
每个三角形底的和高的比相等。
6 : 4= 3 : 2
两个三角形高的比和底的比相等。
4 : 2= 6 : 3
两个三角形底的比和高的比相等。
6 : 3 = 4 : 2
每个三角形的高和底的比相等。
4 : 6= 2 : 3
组成比例的四个数,叫作比例的项。
两端的两项叫作比例的外项,
中间的两项叫作比例的内项。
例如:6 : 3 = 4 : 2
其他三个比例的内项和外项各是多少?
4 : 2 = 6 : 3
6 : 4 = 3 : 2
4 : 6 = 2 : 3
观察上面的四个比例, 你有什么发现?
再写出一些比例, 看看是不是有同样的规律。
6 和 2 可以同时是比
例的外项, 也可以
同时是比例的内项。
3 和 4 可以同时是比
例的内项 , 也可以
同时是比例的外项。
6 × 2 = 3 × 4,
两个外项的积与两
个内项的积相等。
如果用字母表示比例的四个项, 即 a:b = c:d, 那么这个规律可以表示成:
a × d = b × c
在比例里,两个外项的积等于两个内项的积, 这叫作比例的基本性质。
如果把比例写成分数形式,把等号两端的分子、 分母交叉相乘, 结果怎样?
6 × 2 = 3 × 4
巩固练习
应用比例的基本性质,判断下面每组的两个比能否组成比例。
如果能组成比例,把组成的比例写出来。
3.6:1.8 和 0.5:0.25
和 18:24
3.6×0.25=0.9
1.8×0.5=0.9
3.6×0.25=1.8×0.5
所以3.6:1.8=0.5:0.25
×18= ×24
所以 = 18:24
×24=6
×18=6
拓展练习
1. 一列火车从甲城开往乙城, 行驶速度和所需时间如下表:
(1) 从表中选择两组数据,写出一个乘积相等的式子。
(2) 根据上面的等式,写出一个比例。
6 × 80 = 4 × 120
4 : 6 = 80 : 120
拓展练习
2. 根据比例的基本性质, 在括号里填上合适的数。
( ): 6 = 4 : ( )
5 :( )=( ): 8
3
8
10
4
课堂总结
比例的基本性质:
比例
各部分名称
项
外项
内项
两个外项的积等于两个内项的积
数学阅读
黄金分割又称黄金律,是指事物各部分间一定的数学比例关系,即将整体一分为二,较大部分与整体部分的比值等于较小部分与较大部分的比值,其比值约为0.618。
4、解比例
导入新课
1.解下列简易方程,并口述过程。
x÷4=1.8 3(X+2)=18
2.什么叫作比例?比例有什么基本性质?
3.应用比例的基本性质,判断下面哪一组中的两个
比可以组成比例?
6:10和9:15 20:5和4:1 5:1和6:2
探究新知
探究新知
根据题意写出长与宽的比相等的比例,因为放大后照片的宽是未知的,可以用x表示,我们设未知量宽是x厘米,然后按长和宽的比写出比例。
探究新知
巩固练习
巩固练习
巩固练习
巩固练习
巩固练习
巩固练习
巩固练习
巩固练习
拓展练习
课堂总结
解比例
应用比例基本性质求未知数
数学阅读
泰勒斯来到埃及,人们想试探一下他的能力,就问他是否能测量金字塔高度。泰勒斯说可以,但有一个条件——法老必须在场。第二天,法老如约而至,金字塔周围也聚集了不少围观的老百姓。泰勒斯来到金字塔前,阳光把他的影子投在地面上。每过一会儿,他就让人测量他影子的长度,当测量值与他身高完全吻合时,他立刻在大金字塔在地面上的投影处作一记号,然后在丈量金字塔底到投影顶尖的距离。这样,他就报出了金字塔确切的高度。
5、比例尺
导入新课
中国的国土面积大约有960万平方千米。但是我们却能在一张不大的纸上把它画下来,你知道这是为什么吗?
探究新知
红光小学有一块长方形草坪,长50米,宽30米。把这块草坪按一定的比例缩小,画出的平面图长5厘米,宽3厘米。你能分别写出草坪长、宽的图上距离和实际距离的比吗?
图上距离
实际距离
5厘米怎么和50米比呢?
探究新知
5厘米怎么和50米比呢?
图上距离和实际距离的单位不同,先要把它们统一成相同的单位,写出比后再化简。
探究新知
50米=5000厘米
5∶5000=1∶1000
草坪长的图上距离和实际距离的比是1∶1000。
30米=3000厘米
3∶3000=1∶1000
草坪宽的图上距离和实际距离的比是1∶1000。
比例尺
探究新知
一幅图的图上距离和实际距离的比,叫作这幅图的比例尺。
图上距离∶实际距离=比例尺
图上距离
实际距离
=比例尺
或
探究新知
红光小学有一块长方形草坪,长50米,宽30米。把这块草坪按一定的比例缩小,画出的平面图长5厘米,宽3厘米。你能分别写出草坪长、宽的图上距离和实际距离的比吗?
这幅平面图的比例尺是多少?
1∶1000
探究新知
你能说说比例尺1∶1000的含义吗?
比例尺1:1000,表示图上距离是实际距离的 。
11000
?
比例尺1:1000,表示实际距离是图上距离的1000倍。
根据比例尺,可以知道图上距离1厘米表示实际距离10米。
探究新知
比例尺1∶1000还可以这样表示:
它表示图上1厘米的距离相当于实际距离10米。
巩固练习
1.说出下面比例尺的实际意义。
图上1厘米表示实际距离22千米。
图上1厘米表示实际距离15千米。
巩固练习
2.荷花村到杏树村的实际距离是15千米。量出这两个村的图上距离,并算出这幅图的比例尺。
3厘米
15千米=1500000厘米
3∶1500000=1∶500000
这幅图的比例尺是1∶500000。
巩固练习
3.解比例。
3????=6×7
?
????=14
?
23????=10×45
?
????=12
?
15????=2.4×5
?
????=60
?
拓展练习
1.上海到杭州的实际距离大约是180千米,在一幅地图上量得两地间的距离是5厘米。求这幅地图的比例尺。
180千米=18000000厘米
5∶18000000=1∶3600000
答:这幅地图的比例尺是1∶3600000。
拓展练习
2.下面是实验小学体育场的平面图。体育场长150米,宽70米。求这幅图的比例尺,并在括号里填上合适的数。
150米=15000厘米
7.5∶15000=1∶2000
答:这幅图的比例尺是1∶2000。
20
40
60
拓展练习
3.下面是小青从家到梅花山的路线图。
(1)小青家到梅花山的路程大约是多少千米?
图中线段长10.5厘米。
10.5×400=4200(米)
答:小青家到梅花山的路程大约是4.2千米。
4200米=4.2千米
拓展练习
3.下面是小青从家到梅花山的路线图。
(2)小青早上8∶00从家出发,以12千米/时的速度骑自行车去梅花山,需要多少分钟到达?
4.2÷12=0.35(时)
0.35时=21分
答:需要21分钟到达。
课堂总结
比例尺
比例尺的含义
一幅图的图上距离和实际距离的比
表示方法
图上距离∶实际距离=比例尺
图上距离
实际距离
=比例尺
用线段比例尺表示
数学阅读
按照国家规定的标准、图示和比例尺绘制的地图叫作国家基本比例尺地图。我国的国家基本比例尺地图的比例尺有以下11种:
1 ∶500、1 ∶1000、1 ∶2000、1 ∶5000、1 ∶10000、1 ∶25000、1 ∶50000、1 ∶100000、1 ∶200000、1 ∶500000、1 ∶1000000。
6、比例尺的应用
复习导入
求比例尺的方法是:
第一种方法:图上距离:实际距离
第二种方法:
图上距离
实际距离
=比例尺
=比例尺
探究新知
探究新知
(1)图上1厘米的线段表示实际距离8000厘米;
(2)实际距离是图上距离的8000倍;
(3)图上距离是实际距离的 。
8000
1
探究新知
比例尺1:8000
方法一
方法二
方法三
5×8000=40000(厘米) 40000厘米=400米
8000厘米=80米 80×5=400(米)
5
=40000(厘米)
÷
8000
1
探究新知
解:设明华小学到少年宫的实际距离是χ厘米。
5
χ
=
1
8000
40000厘米=400米
方法五
答:明华小学到少年宫的实际距离是400米。
χ= 5×8000
χ= 40000
医院在明华小学的正北方向,它们之间的实际距离是240米。先算出明华小学到医院的图上距离,再在上图中表示出医院的位置。
探究新知
方法二:8000厘米=80米
240÷80=3(厘米)
比例尺1:8000
探究新知
24000 × =3(厘米)
8000
1
240米=24000厘米
方法一:
·
医院
3厘米
下面是梅镇汽车站附近的平面图。
.
.
.
镇政府
汽车站
敬老院
北
巩固练习
比例尺1:20000
(1)分别量出汽车站到镇政府和敬老院的图上距离,再算出实际距离各是多少米。
巩固练习
.
.
.
镇政府
汽车站
敬老院
3 cm
3.5 cm
汽车站到镇政府的实际距离为:
3×20000=60000(厘米)
比例尺1:20000
60000厘米=600米
汽车站到敬老院的实际距离为:3.5×20000=70000(厘米)
70000厘米=700米
北
.
镇政府
比例尺1 : 20000
·
20000厘米=200米
400÷200=2(cm)
.
.
汽车站
敬老院
北
幼儿园
2厘米
(2)幼儿园在汽车站的正西方向400米处,你能在图中表示出幼儿园的位置吗?
“神州”九号载人飞船返回舱着陆在内蒙古的四子王旗。在比例尺是1:15000000的地图上,量得四子王旗与北京的距离是3厘米。两地间的实际距离大约是多少千米?
3×15000000=45000000(厘米)
45000000厘米=450千米
答:两地间的实际距离大约是450千米。
拓展练习
·
街心花园
北
桃林小学在街心花园正东方向650米处,大众超市在桃林小学正北方向200米处。在图中表示出桃林小学和大众超市的位置。
·
桃林小学
·
大众超市
650÷100=6.5(厘米)
200÷100=2(厘米)
1:16000
1400 m
15 cm
3000000厘米=30千米 450÷30=15(厘米)
800米=80000厘米 5:80000=1:16000
3.5×40000=140000(厘米) 140000厘米=1400米
7.下面是小青从家到梅花山的路线图。
(1)小青家到梅花山的路程大约是多少千米?
5+3+2.5=10.5(厘米)
400×10.5=4200(米)
4200米=4.2千米
答:小青家到梅花山的路程大约是4.2千米。
(2)小青早上8:00从家出发,以12千米/时的速度骑自行车去梅花山,需要多少分钟到达?
4.2÷12×60=21(分)
答:需要21分钟到达。
8.找一幅中国地图,量出上海到北京的图上距离,并根据地图的比例尺计算实际距离大约是多少千米。
比例尺1:9000000
12 cm
108000000厘米=1080千米
比例尺1:9000000
图上距离:12厘米
实际距离:9000000×12=108000000(厘米)
答:上海到北京的实际距离大约是1080千米 。
课堂总结
不管是求图上距离还是实际距离,都要弄清题里的条件和问题,再根据“图上距离:实际距离=比例尺”这个关系式列方程,在用实际距离和比例尺求图上距离时,先要把实际距离和图上距离的单位统一,再列方程;在用图上距离和比例尺求实际问题时,求出的实际距离能化成米或千米作单位的数时要化成米或千米作单位的数。
7、面积的变化
导入新课
判断:一幅地图的比例尺是1:1000,那么图上面积与实际面积的比也是1:1000。
提问:这句话对吗?你能说说你的理由吗?
一个长方形的长和宽按比例放大后,面积会按照怎样的规律发生变化呢?
探究新知
下面的大长方形是小长方形按比例放大后得到的。分别量出它们的长和宽,写出对应边长的比。
大长方形与小长方形的长的比是( ):( ),宽的比是( ):( )
3
1
3
1
探究新知
估计一下大长方形和小长方形的面积比是几比几,再算一算,看看你估计的对不对。
怎么验证的?
验证方法:
(1)计算出面积说明。
(2)在大长方形中画小长方形。
探究新知
放大的长方形和原来相比,对应边长度的比是3:1,可是,面积的比却不一样,变成了9:1。你得到了什么结论?
如果大长方形与小长方形对应边的比是4:1,那么面积比是几比几呢?
面积比是16:1。
探究新知
其他平面图形按比例放大后,面积的比又会怎样变化呢?
探究新知
正方形 3:1
三角形 2:1
圆 4:1
估计一下,它们的对应边是按几比几的比放大的?
测量一下,它们的对应边是按几比几的比放大的?
探究新知
这几个图形放大后与放大前的面积相比,发生了怎样的变化?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
放大前
放大后
放大后与放大前的比较
正方形
边长/cm
面积/cm?
三角形
底/cm
高/cm
面积/cm?
圆
半径/cm
面积/cm?
1
0.5
3:1
9:1
2:1
2:1
4:1
4:1
16:1
1
1
1
2
0.25
3
9
4
2
4
2
4
探究新知
比较每个图形放大后与放大前的长度比和面积比,你能发现什么?规律?
如果把一个图形按n:1的比放大,放大后与放大前图形的面积比是( ):( )。
n?
1
巩固练习
1.将面积是8平方厘米的长方形按2:1的比例放大后,得到的长方形的面积是( )平方厘米。
32
想:按2:1的比例放大,面积将扩大到原来的2?=4倍,8×4=32(平方厘米)。
巩固练习
因为放大后与放大前的面积的比是9:1,所以对应高的比是3:1。
解:设放大前的高是x分米。
6:x=3:1
x=2
答:放大前的高是2分米。
2.把一个三角形按一定的比例放大,它们的面积比是9:1,放大后的三角形的高是6分米,放大前的三角形的高是多少?
巩固练习
在第112页的方格纸上画一个平行四边形,按比例放大,算一算放大后与放大前图形的面积比,看看是不是符合上面发现的规律。
如果把一个平面图形按指定的某个比缩小,缩小前后图形面积的变化规律又是什么呢?
拓展练习
一个长方体、正方体或圆柱体按比例放大,如果放大后与放大前图形的对应边长度的比是n:1,那么放大后与放大前图形体积的比是( )。
n?: 1
课堂总结
回顾探索规律的过程,你有什么收获?还想到了什么?
寻找面积的变化规律,要对放大前后的图形进行比较。
认真观察比较数据,才能发现规律。
长方体、正方体按比例放大后,体积比和长度比会有什么关系?
