安徽省安庆市桐城市2020--2021学年度第一学期九年级数学期末统考试卷(word版,含简略答案)
文档属性
| 名称 | 安徽省安庆市桐城市2020--2021学年度第一学期九年级数学期末统考试卷(word版,含简略答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-10 18:59:38 | ||
图片预览



文档简介
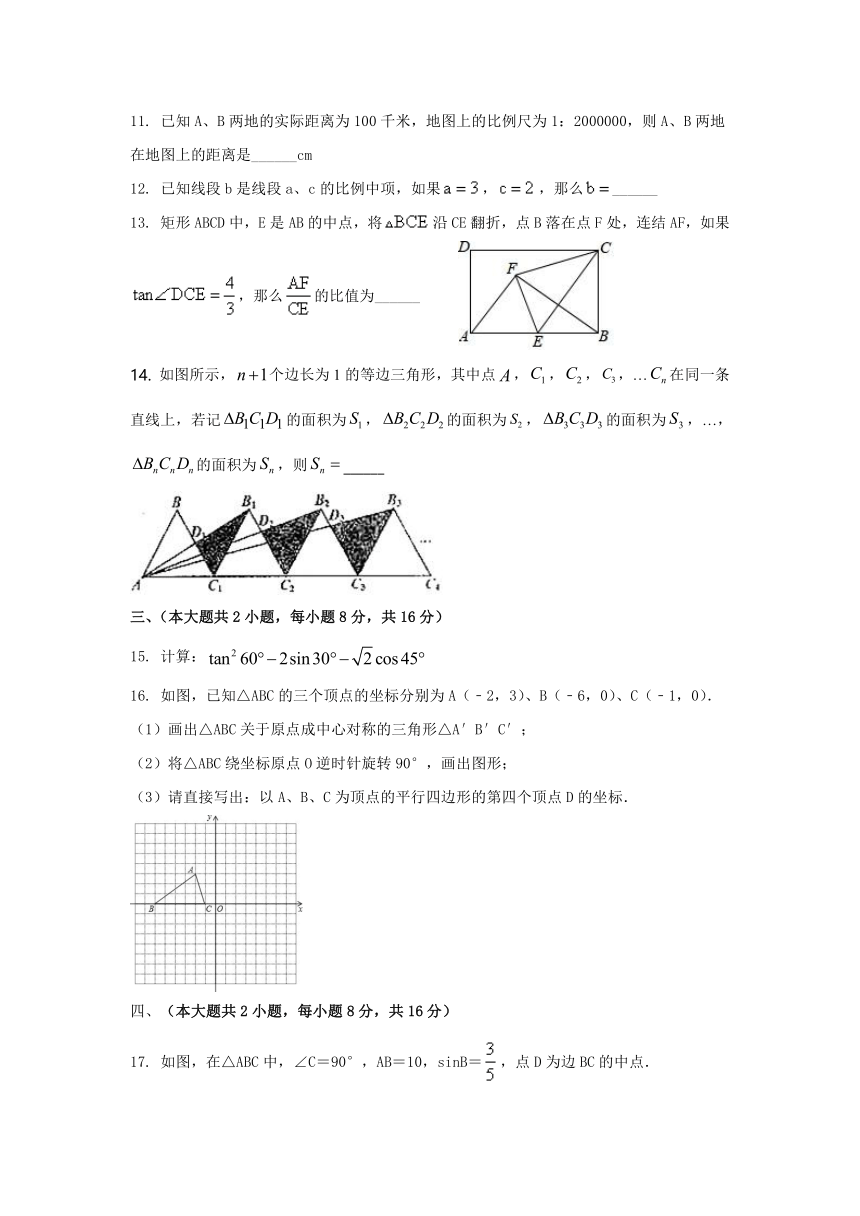
2020--2021学年度第一学期桐城市九年级数学期末统考试卷
一、选择题(本大题共10小题,每小题4分,满分40分)
1.
抛物线y=2(x+3)2+5的顶点坐标是(
)
A.
(3,5)
B.
(﹣3,5)
C.
(3,﹣5)
D.
(﹣3,﹣5)
2.
下列图案中既是中心对称图形,又是轴对称图形的是(
)
A.
B.
C.
D.
3.
如图,点B在线段AC上,且,设AC=2,则AB长为(
)
A.
B.
C.
D.
4.
在中,,于点D,下列式子表示B错误的是
A.
B.
C.
D.
5.
一次函数与二次函数在同一坐标系中的图像可能是(
)
A.
B.
C.
D.
6.
二次函数y=ax2+bx+c的自变量x与函数y的对应值如下表:
x
…
-5
-4
-3
-2
-1
0
…
y
…
4
0
-2
-2
0
4
…
下列说法正确的是(
)
A.
抛物线的开口向下
B.
当x>-3时,y随x的增大而增大
C.
二次函数的最小值是-2
D.
抛物线的对称轴是直线x=-
7.
如图,平面直角坐标系中,点A是x轴上任意一点,BC平行于x轴,分别交y=(x>0)、y=(x<0)的图象于B、C两点,若△ABC的面积为2,则k值为(
)
A.
﹣1
B.
1
C.
D.
8.如下左图,⊙A中,弦BC和弦ED所对的圆心角分别是∠BAC和∠EAD.已知DE=6,∠BAC+∠EAD=180°,则弦BC的弦心距等于(
)
A.
B.
C.
4
D.
3
第8题图
第9题图
如图,在平面直角坐标系中,M、N、C三点的坐标分别为(,1),(3,1),(3,0),点A为线段MN上的一个动点,连接AC,过点A作AB⊥AC交y轴于点B,当点A从M运动到N时,点B随之运动,设点B的坐标为(0,b),则b的取值范围是( )
A.
≤b≤1
B.
≤b≤1
C.
≤b≤
D.
≤b≤1
10.
如图,菱形ABCD中,AB=2,∠B=60°,M为AB的中点.动点P在菱形的边上从点B出发,沿B→C→D的方向运动,到达点D时停止.连接MP,设点P运动的路程为x,MP
2=y,则表示y与x的函数关系的图象大致为( )
A.
B.
C.
D.
二、填空题(本大题共4小题,每小题5分,共20分)
11.
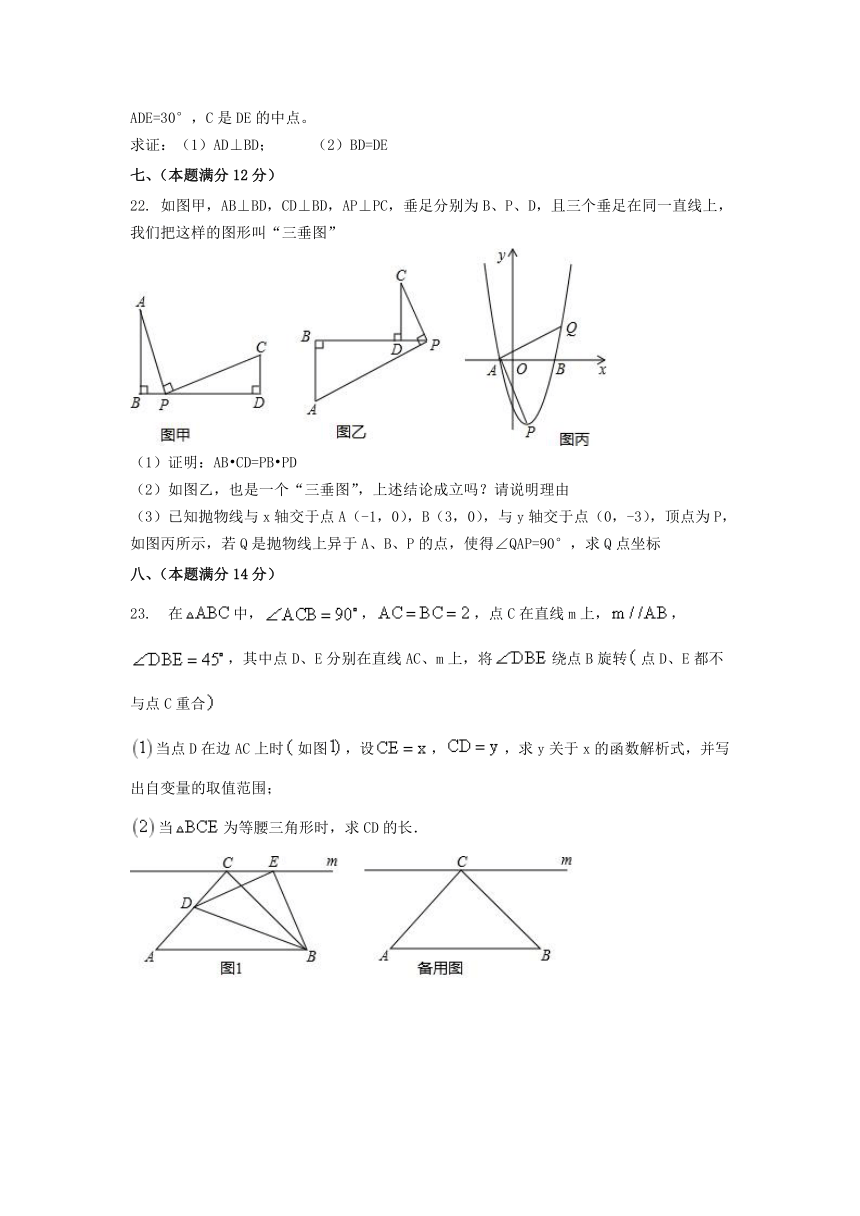
已知A、B两地的实际距离为100千米,地图上的比例尺为1:2000000,则A、B两地在地图上的距离是______cm
12.
已知线段b是线段a、c的比例中项,如果,,那么______
13.
矩形ABCD中,E是AB的中点,将沿CE翻折,点B落在点F处,连结AF,如果,那么的比值为______
14.
如图所示,个边长为1的等边三角形,其中点,,,,…在同一条直线上,若记的面积为,的面积为,的面积为,…,的面积为,则______
三、(本大题共2小题,每小题8分,共16分)
15.
计算:
16.
如图,已知△ABC的三个顶点的坐标分别为A(﹣2,3)、B(﹣6,0)、C(﹣1,0).
(1)画出△ABC关于原点成中心对称的三角形△A′B′C′;
(2)将△ABC绕坐标原点O逆时针旋转90°,画出图形;
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.
(本大题共2小题,每小题8分,共16分)
17.
如图,在△ABC中,∠C=90°,AB=10,sinB=,点D为边BC的中点.
(1)求BC的长.
(2)求∠BAD的正切值.
18.如图,一次函数y=kx+b与反比例函数(x<0)的图像相交于点A、点B,与x轴交于点C,其中点A(-1,3)和点B(-3,n)
填空:m=
;
n=
;
(2)求一次函数的解析式和△AOB的面积;
(3)根据图像回答:当x为何值时,kx+b≤(请直接写出答案)
五、(本大题共2小题,每小题10分,共20分)
19.桐城市某汽车美容店,清洗一辆汽车,当定价20元时每天能清洗45辆,当定价25元时每天能清洗30辆,若清洗汽车辆数y(辆)与定价x(元)(x取整数)是一次函数的关系(清洗每辆汽车成本忽略不计)
(1)求y与x之间的函数表达式;
(2)若清洗一辆汽车定价不低于15元且不超过50元,且该汽车美容店每天需支付电费、水费和员工工资共计200元,问:定价为多少元时,该汽车美容店每天获利最大?最大获利多少元?
20
.如下左图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.
六、(本题满分12分)
21、小明同学用两块含30°的直角三角板如上右图放置,∠ACB=∠AED=90°,∠ABC=∠ADE=30°,C是DE的中点。
求证:(1)AD⊥BD;
(2)BD=DE
七、(本题满分12分)
22.
如图甲,AB⊥BD,CD⊥BD,AP⊥PC,垂足分别为B、P、D,且三个垂足在同一直线上,我们把这样的图形叫“三垂图”
(1)证明:AB?CD=PB?PD
(2)如图乙,也是一个“三垂图”,上述结论成立吗?请说明理由
(3)已知抛物线与x轴交于点A(-1,0),B(3,0),与y轴交于点(0,-3),顶点为P,如图丙所示,若Q是抛物线上异于A、B、P的点,使得∠QAP=90°,求Q点坐标
八、(本题满分14分)
23.
在中,,,点C在直线m上,,,其中点D、E分别在直线AC、m上,将绕点B旋转点D、E都不与点C重合
当点D在边AC上时如图,设,,求y关于x的函数解析式,并写出自变量的取值范围;
当为等腰三角形时,求CD的长.
九年级数学期末试卷答案
1.B
2.C
3.C
4.D
5.C
6.D
7.A
8.D
9.B
10.B
11.5
12.
13.
14.
15.
1
16.(1)图略
(2)图略
(3)D(-7,3)或(3,3)或(-5,-3)
17.
(1)BC=8
(2)17/6
18.
(1)∵反比例函数过点A(-1,3),B(-3,n),∴
m=3×(-1)=-3,-3=-3n,∴
n=1
故答案为-3,1
(2)设一次函数解析式y=kx+b,且过(-1,3),B(-3,1)∴解得:
∴解析式y=x+4,∵一次函数图象与x轴交点为C,∴0=x+4,∴x=-4,∴C(-4,0),∵S△AOB=S△AOC-S△BOC,
∴S△AOB=×4×3-×4×1=4
(3)∵kx+b≤;∴一次函数图象在反比例函数图象下方∴x≤-3或0<x≤-1,故答案为x≤-3或0<x≤-1。
19.(1)设y与x的一次函数式为y=kx+b,由题意可知:,解得:,
所以y=-3x+105
(2)设汽车美容店每天获利润为w元;由题意可知w=xy-200=x(-3x+105)-200=-3(x-17.5)2-718.75
因为15≤x≤50;且x为整数,所以当x=17或18时,w最大=718元
20.(1)证明:连接OD,AD
∵AB是⊙O的直径
∴AD⊥BC
又∵AB=AC
∴D是BC的中点
∵O是AB的中点
∴OD是△ABC的中位线
∴OD∥AC
∵DF是⊙O的切线
∴OD⊥DF
∴DF⊥AC
(2)解:连接OE
由(1)可知DF⊥AC
∴∠CFD=90°
∵∠CDF=22.5°
∴∠C=90°-∠CDF=67.5°
∵AB=AC
∴∠B=∠C=67.5°
∴∠BAC=45°
∵OA=OE=4∴∠AEO=∠OAE=45°∴∠AOE=90°
S阴影=360
(90π×42)-2
(1)×4×4=4π-8
21.
(1)∵∠ACB=∠AED=90°,∠ABC=∠ADE=30°;
∴△ACB∽△AED;
∴
∵∠BAC=∠DAE=60°,∴∠BAD=∠CAE;∴△ABD∽△ACE;∴∠ADB=∠AEC=90°;∴AD⊥BD.
(2)由(1)得△ABD∽△ACE;∴;∴BD=2CE;又∵C是DE中点,∴DE=2CE;∴BD=DE
22.
2
23.
.
,,
.
∽.
,即.
;
当时,C、D重合,不符合题意,舍去;
当时,如图1,,
,
.
则.
.
,
是等腰直角三角形.
,
;
当时,
Ⅰ如图2,,
.
.
.
,
.
;
Ⅱ如图3,则,
.
,
,
.
.
.
所以当为等腰三角形时,CD的长为2或或.
一、选择题(本大题共10小题,每小题4分,满分40分)
1.
抛物线y=2(x+3)2+5的顶点坐标是(
)
A.
(3,5)
B.
(﹣3,5)
C.
(3,﹣5)
D.
(﹣3,﹣5)
2.
下列图案中既是中心对称图形,又是轴对称图形的是(
)
A.
B.
C.
D.
3.
如图,点B在线段AC上,且,设AC=2,则AB长为(
)
A.
B.
C.
D.
4.
在中,,于点D,下列式子表示B错误的是
A.
B.
C.
D.
5.
一次函数与二次函数在同一坐标系中的图像可能是(
)
A.
B.
C.
D.
6.
二次函数y=ax2+bx+c的自变量x与函数y的对应值如下表:
x
…
-5
-4
-3
-2
-1
0
…
y
…
4
0
-2
-2
0
4
…
下列说法正确的是(
)
A.
抛物线的开口向下
B.
当x>-3时,y随x的增大而增大
C.
二次函数的最小值是-2
D.
抛物线的对称轴是直线x=-
7.
如图,平面直角坐标系中,点A是x轴上任意一点,BC平行于x轴,分别交y=(x>0)、y=(x<0)的图象于B、C两点,若△ABC的面积为2,则k值为(
)
A.
﹣1
B.
1
C.
D.
8.如下左图,⊙A中,弦BC和弦ED所对的圆心角分别是∠BAC和∠EAD.已知DE=6,∠BAC+∠EAD=180°,则弦BC的弦心距等于(
)
A.
B.
C.
4
D.
3
第8题图
第9题图
如图,在平面直角坐标系中,M、N、C三点的坐标分别为(,1),(3,1),(3,0),点A为线段MN上的一个动点,连接AC,过点A作AB⊥AC交y轴于点B,当点A从M运动到N时,点B随之运动,设点B的坐标为(0,b),则b的取值范围是( )
A.
≤b≤1
B.
≤b≤1
C.
≤b≤
D.
≤b≤1
10.
如图,菱形ABCD中,AB=2,∠B=60°,M为AB的中点.动点P在菱形的边上从点B出发,沿B→C→D的方向运动,到达点D时停止.连接MP,设点P运动的路程为x,MP
2=y,则表示y与x的函数关系的图象大致为( )
A.
B.
C.
D.
二、填空题(本大题共4小题,每小题5分,共20分)
11.
已知A、B两地的实际距离为100千米,地图上的比例尺为1:2000000,则A、B两地在地图上的距离是______cm
12.
已知线段b是线段a、c的比例中项,如果,,那么______
13.
矩形ABCD中,E是AB的中点,将沿CE翻折,点B落在点F处,连结AF,如果,那么的比值为______
14.
如图所示,个边长为1的等边三角形,其中点,,,,…在同一条直线上,若记的面积为,的面积为,的面积为,…,的面积为,则______
三、(本大题共2小题,每小题8分,共16分)
15.
计算:
16.
如图,已知△ABC的三个顶点的坐标分别为A(﹣2,3)、B(﹣6,0)、C(﹣1,0).
(1)画出△ABC关于原点成中心对称的三角形△A′B′C′;
(2)将△ABC绕坐标原点O逆时针旋转90°,画出图形;
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.
(本大题共2小题,每小题8分,共16分)
17.
如图,在△ABC中,∠C=90°,AB=10,sinB=,点D为边BC的中点.
(1)求BC的长.
(2)求∠BAD的正切值.
18.如图,一次函数y=kx+b与反比例函数(x<0)的图像相交于点A、点B,与x轴交于点C,其中点A(-1,3)和点B(-3,n)
填空:m=
;
n=
;
(2)求一次函数的解析式和△AOB的面积;
(3)根据图像回答:当x为何值时,kx+b≤(请直接写出答案)
五、(本大题共2小题,每小题10分,共20分)
19.桐城市某汽车美容店,清洗一辆汽车,当定价20元时每天能清洗45辆,当定价25元时每天能清洗30辆,若清洗汽车辆数y(辆)与定价x(元)(x取整数)是一次函数的关系(清洗每辆汽车成本忽略不计)
(1)求y与x之间的函数表达式;
(2)若清洗一辆汽车定价不低于15元且不超过50元,且该汽车美容店每天需支付电费、水费和员工工资共计200元,问:定价为多少元时,该汽车美容店每天获利最大?最大获利多少元?
20
.如下左图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.
六、(本题满分12分)
21、小明同学用两块含30°的直角三角板如上右图放置,∠ACB=∠AED=90°,∠ABC=∠ADE=30°,C是DE的中点。
求证:(1)AD⊥BD;
(2)BD=DE
七、(本题满分12分)
22.
如图甲,AB⊥BD,CD⊥BD,AP⊥PC,垂足分别为B、P、D,且三个垂足在同一直线上,我们把这样的图形叫“三垂图”
(1)证明:AB?CD=PB?PD
(2)如图乙,也是一个“三垂图”,上述结论成立吗?请说明理由
(3)已知抛物线与x轴交于点A(-1,0),B(3,0),与y轴交于点(0,-3),顶点为P,如图丙所示,若Q是抛物线上异于A、B、P的点,使得∠QAP=90°,求Q点坐标
八、(本题满分14分)
23.
在中,,,点C在直线m上,,,其中点D、E分别在直线AC、m上,将绕点B旋转点D、E都不与点C重合
当点D在边AC上时如图,设,,求y关于x的函数解析式,并写出自变量的取值范围;
当为等腰三角形时,求CD的长.
九年级数学期末试卷答案
1.B
2.C
3.C
4.D
5.C
6.D
7.A
8.D
9.B
10.B
11.5
12.
13.
14.
15.
1
16.(1)图略
(2)图略
(3)D(-7,3)或(3,3)或(-5,-3)
17.
(1)BC=8
(2)17/6
18.
(1)∵反比例函数过点A(-1,3),B(-3,n),∴
m=3×(-1)=-3,-3=-3n,∴
n=1
故答案为-3,1
(2)设一次函数解析式y=kx+b,且过(-1,3),B(-3,1)∴解得:
∴解析式y=x+4,∵一次函数图象与x轴交点为C,∴0=x+4,∴x=-4,∴C(-4,0),∵S△AOB=S△AOC-S△BOC,
∴S△AOB=×4×3-×4×1=4
(3)∵kx+b≤;∴一次函数图象在反比例函数图象下方∴x≤-3或0<x≤-1,故答案为x≤-3或0<x≤-1。
19.(1)设y与x的一次函数式为y=kx+b,由题意可知:,解得:,
所以y=-3x+105
(2)设汽车美容店每天获利润为w元;由题意可知w=xy-200=x(-3x+105)-200=-3(x-17.5)2-718.75
因为15≤x≤50;且x为整数,所以当x=17或18时,w最大=718元
20.(1)证明:连接OD,AD
∵AB是⊙O的直径
∴AD⊥BC
又∵AB=AC
∴D是BC的中点
∵O是AB的中点
∴OD是△ABC的中位线
∴OD∥AC
∵DF是⊙O的切线
∴OD⊥DF
∴DF⊥AC
(2)解:连接OE
由(1)可知DF⊥AC
∴∠CFD=90°
∵∠CDF=22.5°
∴∠C=90°-∠CDF=67.5°
∵AB=AC
∴∠B=∠C=67.5°
∴∠BAC=45°
∵OA=OE=4∴∠AEO=∠OAE=45°∴∠AOE=90°
S阴影=360
(90π×42)-2
(1)×4×4=4π-8
21.
(1)∵∠ACB=∠AED=90°,∠ABC=∠ADE=30°;
∴△ACB∽△AED;
∴
∵∠BAC=∠DAE=60°,∴∠BAD=∠CAE;∴△ABD∽△ACE;∴∠ADB=∠AEC=90°;∴AD⊥BD.
(2)由(1)得△ABD∽△ACE;∴;∴BD=2CE;又∵C是DE中点,∴DE=2CE;∴BD=DE
22.
2
23.
.
,,
.
∽.
,即.
;
当时,C、D重合,不符合题意,舍去;
当时,如图1,,
,
.
则.
.
,
是等腰直角三角形.
,
;
当时,
Ⅰ如图2,,
.
.
.
,
.
;
Ⅱ如图3,则,
.
,
,
.
.
.
所以当为等腰三角形时,CD的长为2或或.
同课章节目录
