五年级数学上册试题 第七单元测试卷3-苏教版(含答案)
文档属性
| 名称 | 五年级数学上册试题 第七单元测试卷3-苏教版(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 578.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-14 00:00:00 | ||
图片预览




文档简介
第七单元测试卷3
一、选择题
1、在下面的数表中,每次框出2个数,一共有 种不同的和.
2
3
4
5
6
7
8
9
10
11
12
13
A.12
B.11
C.10
D.9
二、填空题
2、如图粗线框中三个数的和是6.在表中移动这个框,一共可以得到
个不同的和.
3、把这24个数从小到大排成一行(如表),如果用方框从左到右框数,
(1)每次框2个,可以得到
个不同的和;
(2)每次框3个,可以得到
个不同的和;
(3)每次框4个,可以得到
个不同的和.
4、把这10个数从小到大排成一行(如下表),
(1)如果每次框出2个数,可以得到
个不同的和.
(2)如果每次框出3个数,可以得到
个不同的和.
(3)如果每次框出4个数,可以得到
个不同的和.
(4)如果每次框出5个数,可以得到
个不同的和.
5、在图表中,把相邻的三个数加起来,一共可以得到
个不同的和.
1
2
3
4
5
6
7
8
9
10
11
6、如图是某年某月的月历,认真观察阴影部分五个数的关系.想一想:如果像这种形式的五个数的和为105,则中间的那个数是 .
7、如图是2013年8月的月历卡,用形如的长方形去框月历卡里的日期数,每次同时框出3个数.框出的3个数和最大的是
,一共可以框出
种不同的和.
8、如图是一条带花的彩带.如果剪3朵花连在一起的彩带,一共有
不同的剪法.
9、下面一排圆圈共有15个,如果要给相邻的4个涂上红色.一共有
种不同的涂法.
三、操作题
10、(2016春?江宁区期末)如图是2010年5月的台历.
(1)小明的爸爸每上4天班休息一天,妈妈却是上3天班休息一天,5月2日爸爸、妈妈都在家休息,下一次他们同时在家休息是星期
.
(2)算一算,上表中被阴影覆盖的5个数的和与中间的数有什么关系?(计算后再说明)
(3)如果框出的5个数的和是75,那么这5个数分别是多少,在图中框出来.
(4)一共可以框出
个不同的和.
11、如图是2008年1月的月历表,表中用“十”字框每次框出5个数(不能少框).
(1)用“十”字框任意框几次,框中5个数的和是正中间一个数的
倍.
(2)如果“十”字框正中间一个数为,5个数的和为90,那么的值是
.
四、解答题
12、有趣的月历.
(1)观察月历中加框的4个数,横行与竖列分别有什么规律?
(2)如果选横着相邻的两个日期,它们的和是37.选的是 和 .
(3)如果选竖着相邻的两个日期,它们的和是51,选的是 和 .
13、如图,有一列正整数,任何三个相连的数字之和都是12,
(1)请你把这列数中的空格填写完整.
(2)请你指出,,各代表什么数字.
(3)用,,这三个数字可以组成的两位数和三位数中,能同时被3,5整除的数有哪些?
3
5
4
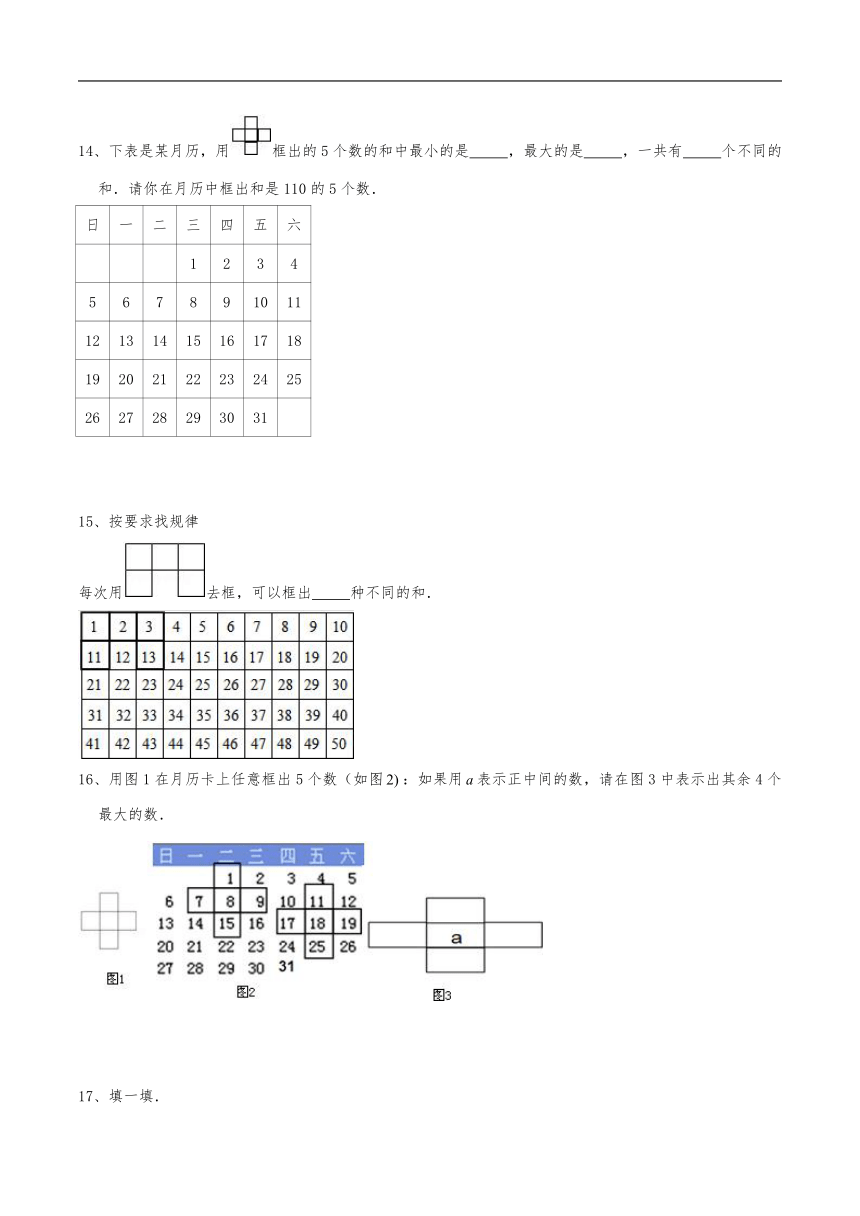
14、下表是某月历,用框出的5个数的和中最小的是
,最大的是
,一共有
个不同的和.请你在月历中框出和是110的5个数.
日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
15、按要求找规律
每次用去框,可以框出
种不同的和.
16、用图1在月历卡上任意框出5个数(如图:如果用表示正中间的数,请在图3中表示出其余4个最大的数.
17、填一填.
如图是2010年6月的月历卡.
一
二
三
四
五
六
日
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
(1)用形如的长方形去框月历卡里的日期数,每次同时框出3个数.框出的3个数的和最大是
,一共可以框出
种不同的和.
(2)如果用形如
的框去框月历卡里的日期数,每次同时框出4个数.框出的4个数的和最大是
,一共可以框出
种不同的和.
18、一般的月历是按一周7天而分成7列来排列的.
(1)你能发现其中的规律吗?(至少写出两条)
(2)用虚线框框住的9个数,如果中间的数用表示,则括号里的各数用式子表示分别是:
、
、
、
.
19、将自然数排列如下,
在这个数阵里,小明用正方形框出九个数.
(1)任意移动几次,每次框住的9个数和与中间的数有什么关系?
(2)如果框住的9个数的和是225,你能列方程,求出中间的一个数吗?
20、下面是2008年6月的日历
日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
①像这种形式的哪5个数的和是100,在图中用阴影表示出这5个数.
②能找到和是120的这样的五个数吗?为什么?
21、想一想,填一填.
用上面的图形在左边表里框出5个数,先算出这5个数的和,再想想算出的和与中间一个数有什么关系?如果5个数的和为795,请在上面图形里写出这5个数.
22、如图是2006年5月的台历,用“”形框数,每次框住5个数.
(1)如果框出的数最小是4,那么框出的5个数的平均数是多少?
(2)在右图中一共可以框出住
个不同的和.
(3)如果框出的5个数中,必须有1个数在周三,那么有
种不同的框法.
23、如图是某年3月的月历,用形如的长方形去框月历里的日期数,每次同时框3个数.
(1)框里三个数的和最大是多少?最小呢?
(2)一共可以框出多少个不同的和?
(3)能框出和是57的3个数吗?如果能,写出这三个数分别是多少?
24、探索与实践:认真观察月历表的规律,如图阴影方框中正中间的数与其他四个数的关系.
(1)正中间的数是,左边的数是 ,右边的数是 ,上面的数是 ,下面的数是 .
(2)方框中5个数之和与该方框正中间的数有什么关系?
(3)当5个数的和是115时,正中间的数是 .
25、下面是2006年6月的月历,认真观察阴影部分五个数的关系.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
根据你发现的规律想一想:像这样形式的哪五个数的和是115,请你用阴影画出这五个数.
26、下表中粗线框中三个数的和是9.在表中移动这个粗线框,可以使每次框出的三个数的和各不相同.
(1)一共可以框出多少个不同的和?
(2)能框出和是64的三个数吗?为什么?
27、如图,是一张的方格纸,它是由16个同样大小的正方形组成的,而且每个正方形里都写了一个数.
(1)从图中去掉一个一共有多少种不同的方法?
(2)如果去掉的四个数的和是46,这四个数应在图中什么位置?(涂色表示)
28、右图里阴影部分框出的4个数之和为48,移动这个框可以使每次框出的4个数的和各不相同.一共可以框出多少个不同的和?
29、下面是2006年5月的台历,用“”形框,每次框住5个数.
(1)如果框住的数最小是4,那么框住的5个数的平均数是多少?
(2)一共可以框住多少个不同数的和?
(3)如果框住的5个数中,有3个数都在周三,那么有几种不同的排法?
30、一列数按如下顺序排列,现在框中五个数的和是50,移动这个框,可以使每次框出的五个数的和各不相同.
(1)如果框出的五个数的和是110,这五个数中最大的一个数是多少?
(2)如果框出的五个数中不能含有20,一共可以框出多少个不同的和?
答案
一、选择题
1、解:数字数:(个)
不同的和数:(个)
答:一共有11种不同的和.
故选:.
二、填空题
2、解:相邻的三个数从1到9每三个数一个框共有9种不同的和,从9开始后面的数字都相同,它们的和也相同只有一种情况,所以共有种不同的和.
故答案为:10.
3、解:根据题干分析可得:
(1)如果每次框出2个数,可以得到23个不同的和.
(2)如果每次框出3个数,可以得到22个不同的和.
(3)如果每次框出4个数,可以得到21个不同的和.
故答案为:23;22;21.
4、解:根据题干分析可得:
(1)如果每次框出2个数,可以得到9个不同的和.
(2)如果每次框出3个数,可以得到8个不同的和.’
(3)如果每次框出4个数,可以得到7个不同的和.
(4)每次框5个数,一共可以得到6个不同的和.
故答案为:9;8;7;6.
5、解:(个).
答:一共可以得到9个不同的和.
故答案为:9.
6、解:因为像这种形式五个数的和是105,
那么五个数的和是中间的数的5倍,
所以中间的数是:,
即中间的那个数是21.
故答案为:21.
7、解:
(种)
答:框出的3个数和最大的是
90,一共可以框出
21种不同的和.
故答案为:90,21.
8、解:(种)
答:一共有6种不同的剪法.
故答案为:6种.
9、解:(种);
答:一共有12种不同的涂法.
故答案为:12.
三、操作题
10、解:(1)5和4是互质数,所以5和4的最小公倍数是:,
所以5月2日,他们同时休息,那么下一次他们同时休息是:,即5月22日,星期六;
(2)上表中被阴影覆盖的5个数和是:;
,所以这5个数的和是中间的数的5倍;
(3)因为这5个数的和是中间的数的5倍,所以中间数是,则框出的5个数为:8、14、15、16、22;
如图:
(4)(个)
所以,一共可以框出11个不同的和.
故答案为:六、11.
11、解:(1)
所以可得:框出的5个数的和是中间数的5倍.
(2)
答:的值是18;
故答案为:5,18.
四、解答题
12、解:(1)观察日历,有这样的规律:
横着相邻的两个日期:右边的数比左边的数大1,
竖着相邻的两个日期:下边的数比上边的数大7;
(2)
答:如果它们的和是37.选的是18和19.
(3)
答:如果它们的和是51,选的是22和29.
故答案为:18,19;22,29.
13、解:(1)填表如下:
4
5
3
4
5
3
4
5
3
4
5
3
(2),,;
(3)由,,这三个数字可以组成的两位数和三位数有:34,43,35,53,45,54,345,354,435,453,534,543,其中同时被3,5整除的数有:45、345、435.
14、解:(1)要使框出的5个数的和最大,框出的5个数为:16、22、23、24、30
和是:;
(2)要使框出的5个数的和最小,框出的5个数为:1、7、8、9、15
和是:;
(3)(种);
(4)(2)根据发现的规律可得:
中间的数是
最上面的一个数是
最左面的一个数是
最右面的一个数是
最下面的一个数是
如图:
故答案为:40,115,12.
15、解:(种)
答:可以框出32种不同的和.
故答案为:32.
16、解:框出的五个数中,两边的两个数的和是中间的数的2倍,所以这五个数为16,22,23,24,30
17、解:(1)
(种)
(2)
(种)
故答案为:(1)87,20;(2)109,16.
18、解:(1)左右时期相差是1天,上下日期相差是7天,某日期与左角上或右下角日期相差8天,与左下角或右上角日期相差6天;
(2)括号里的各数用式子表示分别是:、、、.
故答案为:左右时期相差是1天,上下日期相差是7天,、、、.
19、解:(1)
如果框出的9个数是1、2、3,9、10、11,17、18、19
答:每次框住的9个数和是中间的数的9倍.
(2)设中间的一个数为.根据(1)找出的规律
答:中间的一个数是25.
20、解:①
如图所示:
日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
14
15
16
17
18
22
23
24
25
26
28
29
30
②
因为24的下面没有数字31,所以不能找到和是120的这样的五个数.
21、解:(1)
所以可得:框出的5个数的和是中间数的5倍;
(2)根据规律框出的5个数的和是中间数的5倍可得:中间数是,
所以.
22、解:(1),
,
;
(2)因为第一行、第二行与第三行可以框住5个不同的和,
第二行、第三行与第四行可以框住5个不同的和,
第三行、第四行与第五行可以框住3个不同的和,
所以一共可以框住不同数的和的个数是:,
(3)要使框出的5个数中,必须有1个数在周三,那么第一行、第二行与第三行有3种框法,
第二行、第三行与第四行有3种框法;
第三行、第四行与第五行有1种框法,
由此得出一共有种不同的框法.
答:(1)如果框住的数最小是4,那么框住的5个数的平均数是11,
(2)一共可以框住13个不同数的和.
(3)框出的5个数中,必须有1个数在周三,那么有8种不同的框法.
故答案为:13;8.
23、解:(1)最大:,
最小:;
答:框里三个数的和最大是84,最小是9.
(2)(种),
答:一共可以框出20个不同的和.
(3)设中间的数为,那么前后两个数分别为:,,
前后两个数分别为:,,
答:这三个数分别是:18、19、20.
24、解:(1)由分析得出:
中间数是,则左边的数是,右边的数是,上面的数是,下面的数是;
(2)左边五个数的和是:,70是中间的数14的5倍;右边五个数的和是:,55是中间的数11的5倍;
所以得出:方框中5个数之和是该方框中间的数的5倍
答:方框中5个数之和是该方框中间的数的5倍.
(3)中间的数都是:.
答:当5个数的和是115时,正中间的数是23.
故答案为:(1),,;.
25、解:(1)发现的规律是5个数之和正好是中间数的5倍,十字架中的竖着的三个数是一个相邻两数差为7的数列,横着的三个数是一个邻两数差为1的数列.
(2)因为5个数的和是115,
所以中间的数是:,上面的数是,下面的数是,左边的数是,右边的数是;
故答案为:5个数之和正好是中间数的5倍,十字架中的竖着的三个数是一个相邻两数差为7的数列,横着的三个数是一个邻两数差为1的数列;
26、解:(1)共有15个数字,每次框出3个数字,一共有(种)框法,所以有13个不同的和.
答:一共可以框出13个不同的和.
(2)由题意可知框出的三个数的和是3的倍数,因为64不是3的倍数,所以不能框出和是64的三个数.
答:不能框出和是64的三个数.因为框出的三个数的和是3的倍数,因为64不是3的倍,所以不能框出和是64的三个是.
27、解:(1)根据分析能在的方格纸中找出9个,
所以从图中去掉一个一共有9种不同的方法.
答:从图中去掉一个一共有9种不同的方法.
(2)设这四个数最左边最上边的是,由题意得:
如图:
28、解:由题意及图可知,最上边一行能框的数从3开始,到9结束,能框4次;竖着能框出的数有行,
总共能框:(次),即一共可以框出16个不同的和;
答:一共可以框出16个不同的和.
29、解:(1)
答:如果框住的数最小是4,那么框住的5个数的平均数是11;
(2)因为第一行、第二行与第三行可以框住5个不同的和,
第二行、第三行与第四行可以框住5个不同的和,
第三行、第四行与第五行可以框住3个不同的和,
所以一共可以框住不同数的和的个数是:(个)
答:一共可以框住13个不同数的和.
(3)要使框出的5个数中,有3个数在周三,那么第一行、第二行与第三行有一种框法,第二行、第三行与第四行有一种框法;
第三行、第四行与第五行有一种框法,由此得出一共有种不同的框法;
答:框出的5个数中,必须有3个数在周三,那么有3种不同的框法.
30、解:如图
(1)由分析可知,如果如果框出的五个数的和是110
中间一个数是:(图中绿框)
这五个数中最大的数是30
答:如果框出的五个数的和是110,这五个数中最大的一个数是30.
(2)红框可以向下平称1格、2格.绿框可以向上平移1格、向下平移1格;原来的位置及平移后的位置还可各向右平移1格,这样一共有(个)不同的和.
答:一共可以框出9个不同的和.
一、选择题
1、在下面的数表中,每次框出2个数,一共有 种不同的和.
2
3
4
5
6
7
8
9
10
11
12
13
A.12
B.11
C.10
D.9
二、填空题
2、如图粗线框中三个数的和是6.在表中移动这个框,一共可以得到
个不同的和.
3、把这24个数从小到大排成一行(如表),如果用方框从左到右框数,
(1)每次框2个,可以得到
个不同的和;
(2)每次框3个,可以得到
个不同的和;
(3)每次框4个,可以得到
个不同的和.
4、把这10个数从小到大排成一行(如下表),
(1)如果每次框出2个数,可以得到
个不同的和.
(2)如果每次框出3个数,可以得到
个不同的和.
(3)如果每次框出4个数,可以得到
个不同的和.
(4)如果每次框出5个数,可以得到
个不同的和.
5、在图表中,把相邻的三个数加起来,一共可以得到
个不同的和.
1
2
3
4
5
6
7
8
9
10
11
6、如图是某年某月的月历,认真观察阴影部分五个数的关系.想一想:如果像这种形式的五个数的和为105,则中间的那个数是 .
7、如图是2013年8月的月历卡,用形如的长方形去框月历卡里的日期数,每次同时框出3个数.框出的3个数和最大的是
,一共可以框出
种不同的和.
8、如图是一条带花的彩带.如果剪3朵花连在一起的彩带,一共有
不同的剪法.
9、下面一排圆圈共有15个,如果要给相邻的4个涂上红色.一共有
种不同的涂法.
三、操作题
10、(2016春?江宁区期末)如图是2010年5月的台历.
(1)小明的爸爸每上4天班休息一天,妈妈却是上3天班休息一天,5月2日爸爸、妈妈都在家休息,下一次他们同时在家休息是星期
.
(2)算一算,上表中被阴影覆盖的5个数的和与中间的数有什么关系?(计算后再说明)
(3)如果框出的5个数的和是75,那么这5个数分别是多少,在图中框出来.
(4)一共可以框出
个不同的和.
11、如图是2008年1月的月历表,表中用“十”字框每次框出5个数(不能少框).
(1)用“十”字框任意框几次,框中5个数的和是正中间一个数的
倍.
(2)如果“十”字框正中间一个数为,5个数的和为90,那么的值是
.
四、解答题
12、有趣的月历.
(1)观察月历中加框的4个数,横行与竖列分别有什么规律?
(2)如果选横着相邻的两个日期,它们的和是37.选的是 和 .
(3)如果选竖着相邻的两个日期,它们的和是51,选的是 和 .
13、如图,有一列正整数,任何三个相连的数字之和都是12,
(1)请你把这列数中的空格填写完整.
(2)请你指出,,各代表什么数字.
(3)用,,这三个数字可以组成的两位数和三位数中,能同时被3,5整除的数有哪些?
3
5
4
14、下表是某月历,用框出的5个数的和中最小的是
,最大的是
,一共有
个不同的和.请你在月历中框出和是110的5个数.
日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
15、按要求找规律
每次用去框,可以框出
种不同的和.
16、用图1在月历卡上任意框出5个数(如图:如果用表示正中间的数,请在图3中表示出其余4个最大的数.
17、填一填.
如图是2010年6月的月历卡.
一
二
三
四
五
六
日
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
(1)用形如的长方形去框月历卡里的日期数,每次同时框出3个数.框出的3个数的和最大是
,一共可以框出
种不同的和.
(2)如果用形如
的框去框月历卡里的日期数,每次同时框出4个数.框出的4个数的和最大是
,一共可以框出
种不同的和.
18、一般的月历是按一周7天而分成7列来排列的.
(1)你能发现其中的规律吗?(至少写出两条)
(2)用虚线框框住的9个数,如果中间的数用表示,则括号里的各数用式子表示分别是:
、
、
、
.
19、将自然数排列如下,
在这个数阵里,小明用正方形框出九个数.
(1)任意移动几次,每次框住的9个数和与中间的数有什么关系?
(2)如果框住的9个数的和是225,你能列方程,求出中间的一个数吗?
20、下面是2008年6月的日历
日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
①像这种形式的哪5个数的和是100,在图中用阴影表示出这5个数.
②能找到和是120的这样的五个数吗?为什么?
21、想一想,填一填.
用上面的图形在左边表里框出5个数,先算出这5个数的和,再想想算出的和与中间一个数有什么关系?如果5个数的和为795,请在上面图形里写出这5个数.
22、如图是2006年5月的台历,用“”形框数,每次框住5个数.
(1)如果框出的数最小是4,那么框出的5个数的平均数是多少?
(2)在右图中一共可以框出住
个不同的和.
(3)如果框出的5个数中,必须有1个数在周三,那么有
种不同的框法.
23、如图是某年3月的月历,用形如的长方形去框月历里的日期数,每次同时框3个数.
(1)框里三个数的和最大是多少?最小呢?
(2)一共可以框出多少个不同的和?
(3)能框出和是57的3个数吗?如果能,写出这三个数分别是多少?
24、探索与实践:认真观察月历表的规律,如图阴影方框中正中间的数与其他四个数的关系.
(1)正中间的数是,左边的数是 ,右边的数是 ,上面的数是 ,下面的数是 .
(2)方框中5个数之和与该方框正中间的数有什么关系?
(3)当5个数的和是115时,正中间的数是 .
25、下面是2006年6月的月历,认真观察阴影部分五个数的关系.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
根据你发现的规律想一想:像这样形式的哪五个数的和是115,请你用阴影画出这五个数.
26、下表中粗线框中三个数的和是9.在表中移动这个粗线框,可以使每次框出的三个数的和各不相同.
(1)一共可以框出多少个不同的和?
(2)能框出和是64的三个数吗?为什么?
27、如图,是一张的方格纸,它是由16个同样大小的正方形组成的,而且每个正方形里都写了一个数.
(1)从图中去掉一个一共有多少种不同的方法?
(2)如果去掉的四个数的和是46,这四个数应在图中什么位置?(涂色表示)
28、右图里阴影部分框出的4个数之和为48,移动这个框可以使每次框出的4个数的和各不相同.一共可以框出多少个不同的和?
29、下面是2006年5月的台历,用“”形框,每次框住5个数.
(1)如果框住的数最小是4,那么框住的5个数的平均数是多少?
(2)一共可以框住多少个不同数的和?
(3)如果框住的5个数中,有3个数都在周三,那么有几种不同的排法?
30、一列数按如下顺序排列,现在框中五个数的和是50,移动这个框,可以使每次框出的五个数的和各不相同.
(1)如果框出的五个数的和是110,这五个数中最大的一个数是多少?
(2)如果框出的五个数中不能含有20,一共可以框出多少个不同的和?
答案
一、选择题
1、解:数字数:(个)
不同的和数:(个)
答:一共有11种不同的和.
故选:.
二、填空题
2、解:相邻的三个数从1到9每三个数一个框共有9种不同的和,从9开始后面的数字都相同,它们的和也相同只有一种情况,所以共有种不同的和.
故答案为:10.
3、解:根据题干分析可得:
(1)如果每次框出2个数,可以得到23个不同的和.
(2)如果每次框出3个数,可以得到22个不同的和.
(3)如果每次框出4个数,可以得到21个不同的和.
故答案为:23;22;21.
4、解:根据题干分析可得:
(1)如果每次框出2个数,可以得到9个不同的和.
(2)如果每次框出3个数,可以得到8个不同的和.’
(3)如果每次框出4个数,可以得到7个不同的和.
(4)每次框5个数,一共可以得到6个不同的和.
故答案为:9;8;7;6.
5、解:(个).
答:一共可以得到9个不同的和.
故答案为:9.
6、解:因为像这种形式五个数的和是105,
那么五个数的和是中间的数的5倍,
所以中间的数是:,
即中间的那个数是21.
故答案为:21.
7、解:
(种)
答:框出的3个数和最大的是
90,一共可以框出
21种不同的和.
故答案为:90,21.
8、解:(种)
答:一共有6种不同的剪法.
故答案为:6种.
9、解:(种);
答:一共有12种不同的涂法.
故答案为:12.
三、操作题
10、解:(1)5和4是互质数,所以5和4的最小公倍数是:,
所以5月2日,他们同时休息,那么下一次他们同时休息是:,即5月22日,星期六;
(2)上表中被阴影覆盖的5个数和是:;
,所以这5个数的和是中间的数的5倍;
(3)因为这5个数的和是中间的数的5倍,所以中间数是,则框出的5个数为:8、14、15、16、22;
如图:
(4)(个)
所以,一共可以框出11个不同的和.
故答案为:六、11.
11、解:(1)
所以可得:框出的5个数的和是中间数的5倍.
(2)
答:的值是18;
故答案为:5,18.
四、解答题
12、解:(1)观察日历,有这样的规律:
横着相邻的两个日期:右边的数比左边的数大1,
竖着相邻的两个日期:下边的数比上边的数大7;
(2)
答:如果它们的和是37.选的是18和19.
(3)
答:如果它们的和是51,选的是22和29.
故答案为:18,19;22,29.
13、解:(1)填表如下:
4
5
3
4
5
3
4
5
3
4
5
3
(2),,;
(3)由,,这三个数字可以组成的两位数和三位数有:34,43,35,53,45,54,345,354,435,453,534,543,其中同时被3,5整除的数有:45、345、435.
14、解:(1)要使框出的5个数的和最大,框出的5个数为:16、22、23、24、30
和是:;
(2)要使框出的5个数的和最小,框出的5个数为:1、7、8、9、15
和是:;
(3)(种);
(4)(2)根据发现的规律可得:
中间的数是
最上面的一个数是
最左面的一个数是
最右面的一个数是
最下面的一个数是
如图:
故答案为:40,115,12.
15、解:(种)
答:可以框出32种不同的和.
故答案为:32.
16、解:框出的五个数中,两边的两个数的和是中间的数的2倍,所以这五个数为16,22,23,24,30
17、解:(1)
(种)
(2)
(种)
故答案为:(1)87,20;(2)109,16.
18、解:(1)左右时期相差是1天,上下日期相差是7天,某日期与左角上或右下角日期相差8天,与左下角或右上角日期相差6天;
(2)括号里的各数用式子表示分别是:、、、.
故答案为:左右时期相差是1天,上下日期相差是7天,、、、.
19、解:(1)
如果框出的9个数是1、2、3,9、10、11,17、18、19
答:每次框住的9个数和是中间的数的9倍.
(2)设中间的一个数为.根据(1)找出的规律
答:中间的一个数是25.
20、解:①
如图所示:
日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
14
15
16
17
18
22
23
24
25
26
28
29
30
②
因为24的下面没有数字31,所以不能找到和是120的这样的五个数.
21、解:(1)
所以可得:框出的5个数的和是中间数的5倍;
(2)根据规律框出的5个数的和是中间数的5倍可得:中间数是,
所以.
22、解:(1),
,
;
(2)因为第一行、第二行与第三行可以框住5个不同的和,
第二行、第三行与第四行可以框住5个不同的和,
第三行、第四行与第五行可以框住3个不同的和,
所以一共可以框住不同数的和的个数是:,
(3)要使框出的5个数中,必须有1个数在周三,那么第一行、第二行与第三行有3种框法,
第二行、第三行与第四行有3种框法;
第三行、第四行与第五行有1种框法,
由此得出一共有种不同的框法.
答:(1)如果框住的数最小是4,那么框住的5个数的平均数是11,
(2)一共可以框住13个不同数的和.
(3)框出的5个数中,必须有1个数在周三,那么有8种不同的框法.
故答案为:13;8.
23、解:(1)最大:,
最小:;
答:框里三个数的和最大是84,最小是9.
(2)(种),
答:一共可以框出20个不同的和.
(3)设中间的数为,那么前后两个数分别为:,,
前后两个数分别为:,,
答:这三个数分别是:18、19、20.
24、解:(1)由分析得出:
中间数是,则左边的数是,右边的数是,上面的数是,下面的数是;
(2)左边五个数的和是:,70是中间的数14的5倍;右边五个数的和是:,55是中间的数11的5倍;
所以得出:方框中5个数之和是该方框中间的数的5倍
答:方框中5个数之和是该方框中间的数的5倍.
(3)中间的数都是:.
答:当5个数的和是115时,正中间的数是23.
故答案为:(1),,;.
25、解:(1)发现的规律是5个数之和正好是中间数的5倍,十字架中的竖着的三个数是一个相邻两数差为7的数列,横着的三个数是一个邻两数差为1的数列.
(2)因为5个数的和是115,
所以中间的数是:,上面的数是,下面的数是,左边的数是,右边的数是;
故答案为:5个数之和正好是中间数的5倍,十字架中的竖着的三个数是一个相邻两数差为7的数列,横着的三个数是一个邻两数差为1的数列;
26、解:(1)共有15个数字,每次框出3个数字,一共有(种)框法,所以有13个不同的和.
答:一共可以框出13个不同的和.
(2)由题意可知框出的三个数的和是3的倍数,因为64不是3的倍数,所以不能框出和是64的三个数.
答:不能框出和是64的三个数.因为框出的三个数的和是3的倍数,因为64不是3的倍,所以不能框出和是64的三个是.
27、解:(1)根据分析能在的方格纸中找出9个,
所以从图中去掉一个一共有9种不同的方法.
答:从图中去掉一个一共有9种不同的方法.
(2)设这四个数最左边最上边的是,由题意得:
如图:
28、解:由题意及图可知,最上边一行能框的数从3开始,到9结束,能框4次;竖着能框出的数有行,
总共能框:(次),即一共可以框出16个不同的和;
答:一共可以框出16个不同的和.
29、解:(1)
答:如果框住的数最小是4,那么框住的5个数的平均数是11;
(2)因为第一行、第二行与第三行可以框住5个不同的和,
第二行、第三行与第四行可以框住5个不同的和,
第三行、第四行与第五行可以框住3个不同的和,
所以一共可以框住不同数的和的个数是:(个)
答:一共可以框住13个不同数的和.
(3)要使框出的5个数中,有3个数在周三,那么第一行、第二行与第三行有一种框法,第二行、第三行与第四行有一种框法;
第三行、第四行与第五行有一种框法,由此得出一共有种不同的框法;
答:框出的5个数中,必须有3个数在周三,那么有3种不同的框法.
30、解:如图
(1)由分析可知,如果如果框出的五个数的和是110
中间一个数是:(图中绿框)
这五个数中最大的数是30
答:如果框出的五个数的和是110,这五个数中最大的一个数是30.
(2)红框可以向下平称1格、2格.绿框可以向上平移1格、向下平移1格;原来的位置及平移后的位置还可各向右平移1格,这样一共有(个)不同的和.
答:一共可以框出9个不同的和.
