6.3正方形的性质与判定 课件(共24张PPT)
文档属性
| 名称 | 6.3正方形的性质与判定 课件(共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-19 16:07:49 | ||
图片预览







文档简介
第六章 特殊平行四边形
3 正方形的性质与判定
知识点一 正方形的定义
定义
有一组邻边相等的矩形叫做正方形
重
点
解
读
(1)正方形的定义有两个条件:①有一组邻边相等;②是矩形,这两个条件必须同时具备,缺一不可.
(2)正方形不仅是特殊的平行四边形,而且是特殊的菱形、特殊的矩形,它们的关系如图所示:
例1 下列命题错误的是( )
A.有一组邻边相等的平行四边形是正方形
B.有一组邻边相等的矩形是正方形
C.有一组邻边相等并且有一个角是直角的平行四边形是正方形
D.有一个角是直角的菱形是正方形
例1 下列命题错误的是( )
A.有一组邻边相等的平行四边形是正方形
B.有一组邻边相等的矩形是正方形
C.有一组邻边相等并且有一个角是直角的平行四边形是正方形
D.有一个角是直角的菱形是正方形
解析 由定义可知,正方形是有一组邻边相等的矩形,A不正确,故选A.
答案 A
例1 下列命题错误的是( )
A.有一组邻边相等的平行四边形是正方形
B.有一组邻边相等的矩形是正方形
C.有一组邻边相等并且有一个角是直角的平行四边形是正方形
D.有一个角是直角的菱形是正方形
解析 由定义可知,正方形是有一组邻边相等的矩形,A不正确,故选A.
答案 A
点拨 根据定义判定正方形的方法:先判定是矩形,再证明是正方形
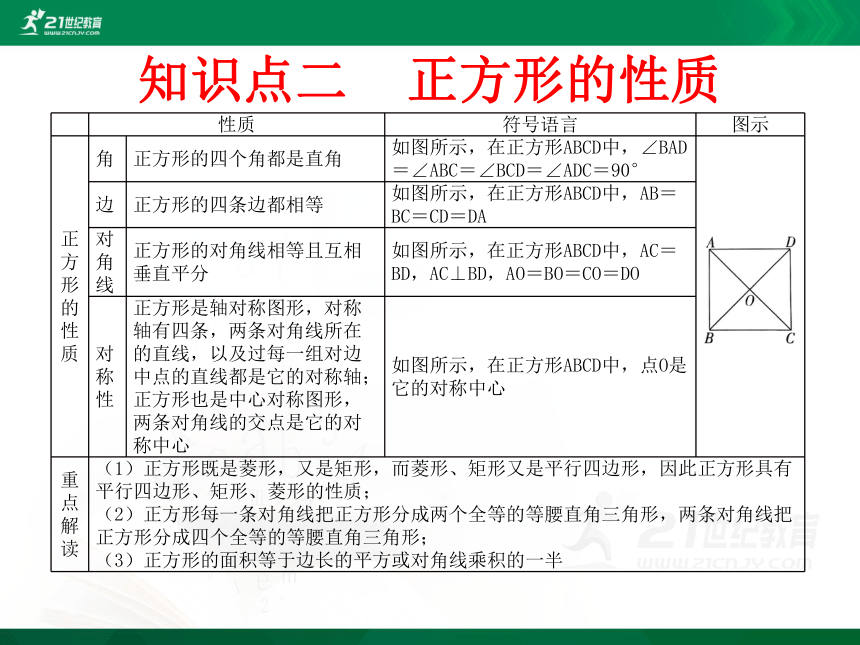
知识点二 正方形的性质
性质
符号语言
图示
正方形的性质
角
边
对角线
对称性
重点解读
知识点二 正方形的性质
性质
符号语言
图示
正方形的性质
角
正方形的四个角都是直角
如图所示,在正方形ABCD中,∠BAD=∠ABC=∠BCD=∠ADC=90°
边
正方形的四条边都相等
如图所示,在正方形ABCD中,AB=BC=CD=DA
对角线
正方形的对角线相等且互相垂直平分
如图所示,在正方形ABCD中,AC=BD,AC⊥BD,AO=BO=CO=DO
对称性
正方形是轴对称图形,对称轴有四条,两条对角线所在的直线,以及过每一组对边中点的直线都是它的对称轴;正方形也是中心对称图形,两条对角线的交点是它的对称中心
如图所示,在正方形ABCD中,点O是它的对称中心
重点解读
(1)正方形既是菱形,又是矩形,而菱形、矩形又是平行四边形,因此正方形具有平行四边形、矩形、菱形的性质;
(2)正方形每一条对角线把正方形分成两个全等的等腰直角三角形,两条对角线把正方形分成四个全等的等腰直角三角形;
(3)正方形的面积等于边长的平方或对角线乘积的一半
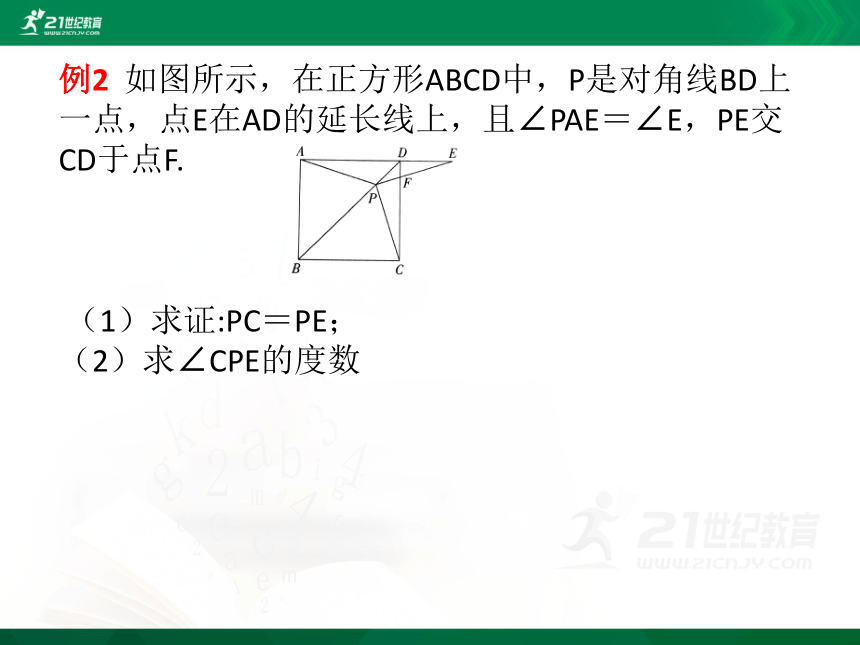
例2 如图所示,在正方形ABCD中,P是对角线BD上一点,点E在AD的延长线上,且∠PAE=∠E,PE交CD于点F.
(1)求证:PC=PE;
(2)求∠CPE的度数
分析 (1)先证出△ADP≌△CDP,得PA=PC,再由PA=PE,得PC=PE;
(2)由△ADP≌△CDP,得∠DAP=∠DCP,进而得∠DCP=∠E,最后∠CPF=∠EDF=90°得到结论.
分析 (1)先证出△ADP≌△CDP,得PA=PC,再由PA=PE,得PC=PE;
(2)由△ADP≌△CDP,得∠DAP=∠DCP,进而得∠DCP=∠E,最后∠CPF=∠EDF=90°得到结论.
解析 (1)证明:在正方形ABCD中,AD=DC,∠ADP=∠CDP=45°,
在△ADP和△CDP中, ∴△ADP≌△CDP(SAS),∴PA=PC.
∵∠PAE=∠E,∴PA=E,∴PC=PE.
(2)在正方形ABCD中,∠ADC=90°,∴∠EDF=90°,
由(1)知,△ADP≌△CDP,∴∠DAP=∠DCP,
∵∠DAP=∠E,∴∠DCP=∠E,
∵∠PFC=∠DFE(对顶角相等),
∴180°-∠PFC-∠PCF=180°-∠DFE-∠E,
即∠CPF=∠EDF=90°.
知识点三 正方形的判定
判定方法
符号语言
图示
正方形的判定
解题思路
知识点三 正方形的判定
判定方法
符号语言
图示
正方形的判定
对角线相等的菱形是正方形
在菱形ABCD中,若AC=BD,则菱形ABCD是正方形
对角线互相垂直的矩形是正方形
在矩形ABCD中,若AC⊥BD,则矩形ABCD是正方形
有一个角是直角的菱形是正方形
在菱形ABCD中,若∠ABC=90°,则菱形ABCD是正方形
解题思路
判定一个四边形是正方形时,先判定它是矩形再判定它是正方思形,或先判定它是菱形,再判定它是正方形
例3 如图所示,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
分析 (1)根据SAS可证明△ABD≌△CBD,从而得∠ADB=∠CDB.(2)先根据“有三个角是直角的四边形是矩形”证得四边形MPND是矩形,再根据“角平分线上的点到角两边的距离相等”得PM=PN,从而证得矩形MPND是正方形.
证明(1)∵BD平分∠ABC,∴∠ABD=∠CBD.
又∵BA=BC,BD=BD,∴△ABD≌△CBD∴∠ADB=∠CDB.
(2)∵PM⊥AD,PN⊥CD,∴∠PMD=∠PND=90°,
又∵∠ADC=90°,∴四边形MPND是矩形.
由(1)知∠ADB=∠CDB,又PM⊥AD,PN⊥CD,∴PM=PN.
∴四边形MPND是正方形.
经典例题
题型一 正方形的性质与判定的综合应用
例1 如图所示,四边形ABCD是正方形,对角线AC、BD相交于点F,∠E=90°,DE=EC.求证:四边形DFCE是正方形.
经典例题
分析 先根据正方形的性质得到∠FDC=∠DCF=45°,再根据DE=EC,∠E=90°,得到∠EDC=∠ECD=45°,从而得到四边形DFCE为矩形,进而证明是正方形.
经典例题
证明 ∵四边形ABCD是正方形,
∴∠FDC=∠DCF=45°∵∠E=90°,ED=EC,
∴∠EDC=∠ECD=45°,
∴∠FCE=∠FDE=∠E=90°,
∴四边形DFCE是矩形,∵DE=CE,
∴四边形DFCE是正方形.
题型二 开放探究题
例2 如图①,一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起现正方形ABCD保持不动,将三角尺GEF绕斜边EF的中点O(点O也是BD中点)按顺时针方向旋转.
(1)如图②,当EF与AB相交于点M,GF与BD相交于点N时,通过观察或测量BM,FN的长度,猜想BM,FN满足的数量关系,并证明你的猜想;
(2)若三角尺GEF旋转到如图③所示的位置时,线段FE的延长线与AB的延长线相交于点M,线段BD的延长线与GF的延长线相交于点N,此时,(1)中的猜想还成立吗?若成立,请证明;若不成立,请说明理由.
分析(1)根据正方形和等腰直角三角形的性质可证明△OBM≌△OFN,所以根据全等的性质可知BM=FN;
(2)同(1)中的证明方法一样,根据正方形和等腰直角三角形的性质得OB=OF,∠MBO=∠NFO=135°,又∠MOB=∠NOF,所以可证△OBM≌△OFN,所以BM=FN.
解析 (1)BM=FN.
证明 ∵△GEF是等腰直角三角形,四边形ABCD是正方形,
∴∠ABD=∠F=45°,OB=OF,
在△OBM与△OFN中, ∴△OBM≌△OFN(ASA),∴BM=FN.
(2)BM=FN仍然成立
证明:∵△GEF是等腰直角三角形,四边形ABCD是正方形,
∴∠DBA=∠GFE=45°,OB=OF,∴∠MBO=∠NFO=135°,
在△OBM与△OFN中, ∴△OB≌△OFN(ASA),∴BM=FN.
易错易混
易错点 没有图形的几何题,因考虑问题不周导致漏解
例 以正方形ABCD的边AD为一边作等边△ADE,则∠AEB的度数为__________.
解析 因为等边三角形ADE可能在正方形的内部,也可能在正方形的外部,所以应分两种情况考虑:
(1)当点E在正方形ABCD的外部时,如图①,
∵四边形ABCD是正方形,∴AB=AD,∠BAD=90°,
∵△ADE是等边三角形,∴AD=AE,∠DAE=60°,
∴∠BAE=∠BAD+∠DAE=150°,AB=AE,
∴∠AEB=∠ABE= =15°.
(2)当点E在正方形ABCD的内部时,如图②,
易知∠BAD=90°,∠DAE=60°,∴∠BAE=∠BAD-∠DAE=30°.
∵AE=AD=AB,∴∠AEB=∠ABE= =75°.
综上,∠AEB的度数为15°或75°.
答案 15°或75°
易错警示 :
对于没有给出图形的几何求解题,要认真分析题意,把满足条件的情况考虑全面,然后分情况讨论解答,不要漏解.
3 正方形的性质与判定
知识点一 正方形的定义
定义
有一组邻边相等的矩形叫做正方形
重
点
解
读
(1)正方形的定义有两个条件:①有一组邻边相等;②是矩形,这两个条件必须同时具备,缺一不可.
(2)正方形不仅是特殊的平行四边形,而且是特殊的菱形、特殊的矩形,它们的关系如图所示:
例1 下列命题错误的是( )
A.有一组邻边相等的平行四边形是正方形
B.有一组邻边相等的矩形是正方形
C.有一组邻边相等并且有一个角是直角的平行四边形是正方形
D.有一个角是直角的菱形是正方形
例1 下列命题错误的是( )
A.有一组邻边相等的平行四边形是正方形
B.有一组邻边相等的矩形是正方形
C.有一组邻边相等并且有一个角是直角的平行四边形是正方形
D.有一个角是直角的菱形是正方形
解析 由定义可知,正方形是有一组邻边相等的矩形,A不正确,故选A.
答案 A
例1 下列命题错误的是( )
A.有一组邻边相等的平行四边形是正方形
B.有一组邻边相等的矩形是正方形
C.有一组邻边相等并且有一个角是直角的平行四边形是正方形
D.有一个角是直角的菱形是正方形
解析 由定义可知,正方形是有一组邻边相等的矩形,A不正确,故选A.
答案 A
点拨 根据定义判定正方形的方法:先判定是矩形,再证明是正方形
知识点二 正方形的性质
性质
符号语言
图示
正方形的性质
角
边
对角线
对称性
重点解读
知识点二 正方形的性质
性质
符号语言
图示
正方形的性质
角
正方形的四个角都是直角
如图所示,在正方形ABCD中,∠BAD=∠ABC=∠BCD=∠ADC=90°
边
正方形的四条边都相等
如图所示,在正方形ABCD中,AB=BC=CD=DA
对角线
正方形的对角线相等且互相垂直平分
如图所示,在正方形ABCD中,AC=BD,AC⊥BD,AO=BO=CO=DO
对称性
正方形是轴对称图形,对称轴有四条,两条对角线所在的直线,以及过每一组对边中点的直线都是它的对称轴;正方形也是中心对称图形,两条对角线的交点是它的对称中心
如图所示,在正方形ABCD中,点O是它的对称中心
重点解读
(1)正方形既是菱形,又是矩形,而菱形、矩形又是平行四边形,因此正方形具有平行四边形、矩形、菱形的性质;
(2)正方形每一条对角线把正方形分成两个全等的等腰直角三角形,两条对角线把正方形分成四个全等的等腰直角三角形;
(3)正方形的面积等于边长的平方或对角线乘积的一半
例2 如图所示,在正方形ABCD中,P是对角线BD上一点,点E在AD的延长线上,且∠PAE=∠E,PE交CD于点F.
(1)求证:PC=PE;
(2)求∠CPE的度数
分析 (1)先证出△ADP≌△CDP,得PA=PC,再由PA=PE,得PC=PE;
(2)由△ADP≌△CDP,得∠DAP=∠DCP,进而得∠DCP=∠E,最后∠CPF=∠EDF=90°得到结论.
分析 (1)先证出△ADP≌△CDP,得PA=PC,再由PA=PE,得PC=PE;
(2)由△ADP≌△CDP,得∠DAP=∠DCP,进而得∠DCP=∠E,最后∠CPF=∠EDF=90°得到结论.
解析 (1)证明:在正方形ABCD中,AD=DC,∠ADP=∠CDP=45°,
在△ADP和△CDP中, ∴△ADP≌△CDP(SAS),∴PA=PC.
∵∠PAE=∠E,∴PA=E,∴PC=PE.
(2)在正方形ABCD中,∠ADC=90°,∴∠EDF=90°,
由(1)知,△ADP≌△CDP,∴∠DAP=∠DCP,
∵∠DAP=∠E,∴∠DCP=∠E,
∵∠PFC=∠DFE(对顶角相等),
∴180°-∠PFC-∠PCF=180°-∠DFE-∠E,
即∠CPF=∠EDF=90°.
知识点三 正方形的判定
判定方法
符号语言
图示
正方形的判定
解题思路
知识点三 正方形的判定
判定方法
符号语言
图示
正方形的判定
对角线相等的菱形是正方形
在菱形ABCD中,若AC=BD,则菱形ABCD是正方形
对角线互相垂直的矩形是正方形
在矩形ABCD中,若AC⊥BD,则矩形ABCD是正方形
有一个角是直角的菱形是正方形
在菱形ABCD中,若∠ABC=90°,则菱形ABCD是正方形
解题思路
判定一个四边形是正方形时,先判定它是矩形再判定它是正方思形,或先判定它是菱形,再判定它是正方形
例3 如图所示,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
分析 (1)根据SAS可证明△ABD≌△CBD,从而得∠ADB=∠CDB.(2)先根据“有三个角是直角的四边形是矩形”证得四边形MPND是矩形,再根据“角平分线上的点到角两边的距离相等”得PM=PN,从而证得矩形MPND是正方形.
证明(1)∵BD平分∠ABC,∴∠ABD=∠CBD.
又∵BA=BC,BD=BD,∴△ABD≌△CBD∴∠ADB=∠CDB.
(2)∵PM⊥AD,PN⊥CD,∴∠PMD=∠PND=90°,
又∵∠ADC=90°,∴四边形MPND是矩形.
由(1)知∠ADB=∠CDB,又PM⊥AD,PN⊥CD,∴PM=PN.
∴四边形MPND是正方形.
经典例题
题型一 正方形的性质与判定的综合应用
例1 如图所示,四边形ABCD是正方形,对角线AC、BD相交于点F,∠E=90°,DE=EC.求证:四边形DFCE是正方形.
经典例题
分析 先根据正方形的性质得到∠FDC=∠DCF=45°,再根据DE=EC,∠E=90°,得到∠EDC=∠ECD=45°,从而得到四边形DFCE为矩形,进而证明是正方形.
经典例题
证明 ∵四边形ABCD是正方形,
∴∠FDC=∠DCF=45°∵∠E=90°,ED=EC,
∴∠EDC=∠ECD=45°,
∴∠FCE=∠FDE=∠E=90°,
∴四边形DFCE是矩形,∵DE=CE,
∴四边形DFCE是正方形.
题型二 开放探究题
例2 如图①,一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起现正方形ABCD保持不动,将三角尺GEF绕斜边EF的中点O(点O也是BD中点)按顺时针方向旋转.
(1)如图②,当EF与AB相交于点M,GF与BD相交于点N时,通过观察或测量BM,FN的长度,猜想BM,FN满足的数量关系,并证明你的猜想;
(2)若三角尺GEF旋转到如图③所示的位置时,线段FE的延长线与AB的延长线相交于点M,线段BD的延长线与GF的延长线相交于点N,此时,(1)中的猜想还成立吗?若成立,请证明;若不成立,请说明理由.
分析(1)根据正方形和等腰直角三角形的性质可证明△OBM≌△OFN,所以根据全等的性质可知BM=FN;
(2)同(1)中的证明方法一样,根据正方形和等腰直角三角形的性质得OB=OF,∠MBO=∠NFO=135°,又∠MOB=∠NOF,所以可证△OBM≌△OFN,所以BM=FN.
解析 (1)BM=FN.
证明 ∵△GEF是等腰直角三角形,四边形ABCD是正方形,
∴∠ABD=∠F=45°,OB=OF,
在△OBM与△OFN中, ∴△OBM≌△OFN(ASA),∴BM=FN.
(2)BM=FN仍然成立
证明:∵△GEF是等腰直角三角形,四边形ABCD是正方形,
∴∠DBA=∠GFE=45°,OB=OF,∴∠MBO=∠NFO=135°,
在△OBM与△OFN中, ∴△OB≌△OFN(ASA),∴BM=FN.
易错易混
易错点 没有图形的几何题,因考虑问题不周导致漏解
例 以正方形ABCD的边AD为一边作等边△ADE,则∠AEB的度数为__________.
解析 因为等边三角形ADE可能在正方形的内部,也可能在正方形的外部,所以应分两种情况考虑:
(1)当点E在正方形ABCD的外部时,如图①,
∵四边形ABCD是正方形,∴AB=AD,∠BAD=90°,
∵△ADE是等边三角形,∴AD=AE,∠DAE=60°,
∴∠BAE=∠BAD+∠DAE=150°,AB=AE,
∴∠AEB=∠ABE= =15°.
(2)当点E在正方形ABCD的内部时,如图②,
易知∠BAD=90°,∠DAE=60°,∴∠BAE=∠BAD-∠DAE=30°.
∵AE=AD=AB,∴∠AEB=∠ABE= =75°.
综上,∠AEB的度数为15°或75°.
答案 15°或75°
易错警示 :
对于没有给出图形的几何求解题,要认真分析题意,把满足条件的情况考虑全面,然后分情况讨论解答,不要漏解.
