人教版必修1 第三章 第五节 力的分解:21张PPT
文档属性
| 名称 | 人教版必修1 第三章 第五节 力的分解:21张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-02-10 20:42:08 | ||
图片预览






文档简介
力的分解
DECOMPOSITION OF THE FORCE
第三章:相互作用
新课引入
1、在作用效果相同的情况下,几个力可以用一个力来替代。问:在作用效果相同的情况下,一个力能否用几个力来替代呢?
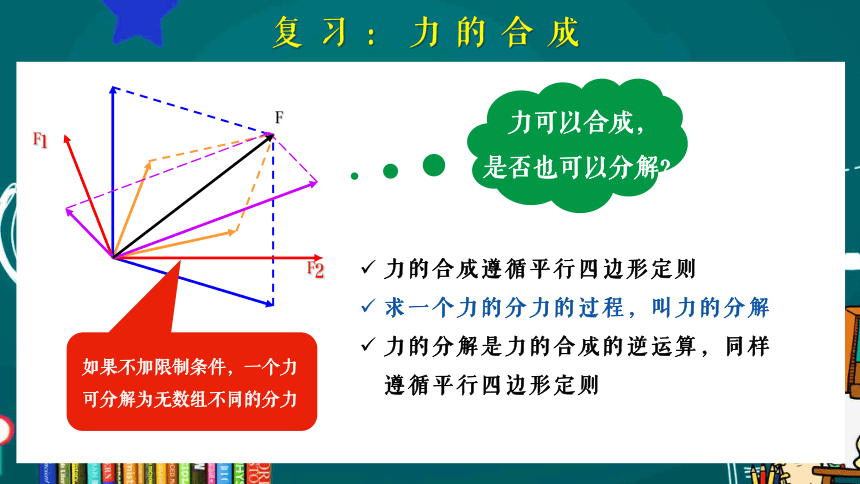
复习:力的合成
F1
F2
F
力的合成遵循平行四边形定则
求一个力的分力的过程,叫力的分解
力的分解是力的合成的逆运算,同样遵循平行四边形定则
力可以合成,
是否也可以分解?
如果不加限制条件,一个力可分解为无数组不同的分力
思 考
不加限制的条件下,一个力可分解为无数组不同的分力。
那么实际处理力的分解时又该如何进行呢?
力的分解
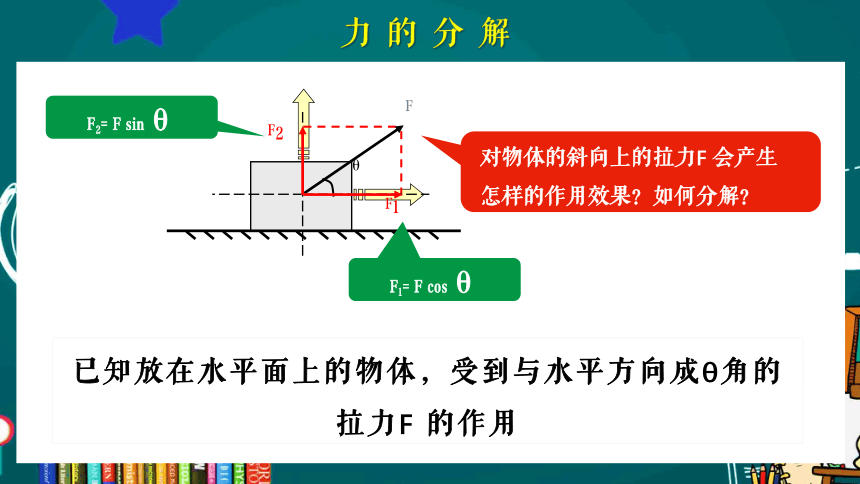
F2= F sinθ
θ
F
F1
F2
F1= F cosθ
已知放在水平面上的物体,受到与水平方向成θ角的拉力F 的作用
对物体的斜向上的拉力F 会产生怎样的作用效果?如何分解?
力的分解
θ
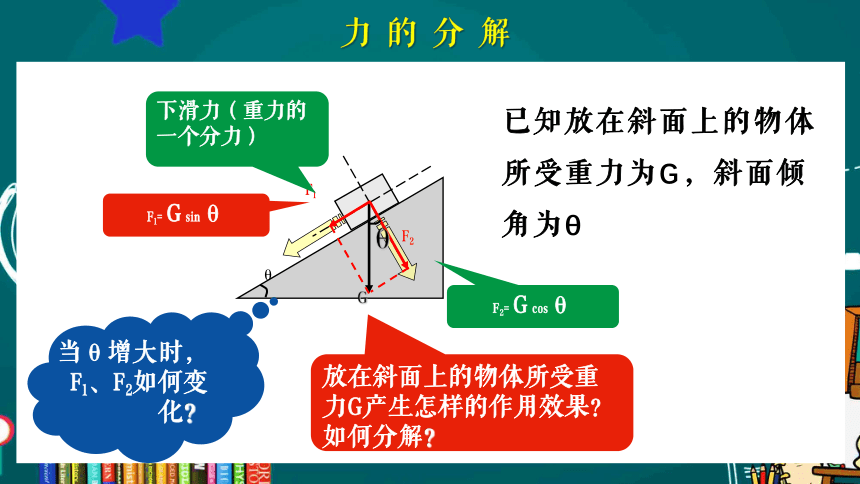
放在斜面上的物体所受重力G产生怎样的作用效果?如何分解?
G
F1= G sinθ
F2
F1
下滑力(重力的一个分力)
θ
F2= G cosθ
当θ增大时,F1、F2如何变化?
已知放在斜面上的物体所受重力为G,斜面倾角为θ
实例分析
思考题
1 当斜面倾角θ增大时分析F1和F2如何变化?
2 当倾角θ减少时,F1和F2如何变化?
当θ增大时,F1增大,F2减小。
当θ减小时,F1减小,F2增大。
斜面上物体的重力的分解是否是惟一?
思考题
要使一个力的分解是惟一的,对两分力有什么要求?
①已知两个分力的方向(不在同一直线上)
②已知一个分力的大小和方向
力的分解
二、矢量相加的法则
1、平行四边形定则在位移运算中的应用
人从A到B,再到C的过程中,总位移与两段位移的关系。
A
B
C
X1
X2
X
力的分解
2、三角形定则
把两个矢量首尾连接求出合矢量的方法。
三角形定则与平行四边形定则实质一样.
C
B
A
两个矢量首尾相接,从第一个矢量的始端指向第二个矢量的末端的有向线段就表示合矢量的大小和方向.
力的分解
F1
F2
F
F4
F3
F1
F2
F4
F3
力的分解
一个物体的速度V1在一小段时间内发生了变化,变成了V2,你能根据三角形定则找出变化量ΔV吗?
3、矢量和标量
矢量:有大小,又有方向,相加时遵循平行四边形定则
标量:有大小,没有方向,求和时按算术法则相加
V1
V2
ΔV
说一说
力的分解
F1= G cosθ
F2= G sinθ
悬挂着的物体所受重力G产生怎样的作用效果?如何分解?
θ
F1
F2
G
θ
A
B
O
用两根轻绳将物体悬挂起来。已知物体重力为G,轻绳AO与水平方向夹角为θ,AOB为直角
分解力的步骤
1、分析力的作用效果。
2、根据力的作用效果确定分力的方向。
输入3、由平行四边形定则确定分力的大小。你的标题
力的分解
θ
F2= G cosθ
G
F1
F2
θ
θ
F1
F2
G
θ
F1= G sinθ
F1= G tanθ
F2= G/cosθ
放在斜面上的物体所受重力G产生怎样的作用效果?如何分解?
力的分解
F1= F /sinθ
F2= F cotθ
A
B
C
θ
F
F1
θ
A
B
C
θ
F
F1
θ
F2
F1= F cotθ
F2= F /sinθ
F2
作用在三角支架上的力F 的作用效果怎样?如何分解?
可自由转动的轻杆AC 和BC ,BC 杆水平。在它们的连接处C点施加一个竖直向下的力F
力的分解
3、如图所示,质量为m的木块在力F作用下在水平面上做匀速运动。木块与地面间的动摩擦因数为?,则物体受到的摩擦力为( )
?
F
?mg
?(mg+Fsin?)
?(mg-Fsin?)
Fcos?
B、D
力的分解的解的个数
F大小、方向
F1大小、方向
F2大小、方向
1.已知合力和两个分力的方向
唯一解
2.已知合力和一个分力的大小和方向
唯一解
3.已知合力和两个分力的大小
两组解
(F1+F2>F且F1≠F2)
(F1、F2不在同一直线上)
若(F1+F2>F且F1=F2) 一组解
力的分解
4.已知合力F及一个分力F2的大小和另一个分力F1的方向 (F1与F的夹角为θ)
①当F2②当F2=Fsinθ时,一组解
③当Fsinθ④当F2>F时,一组解
θ为锐角时:
θ为钝角时:
①当F2≤F时,无解 ②当F2>F时,一组解
课堂小结
一、原则:根据力的实际作用效果分解
二、方法:平行四边形定则(解三角形)
02
01
03
04
已知一个分力的方向和另一个分力的大小 (两解、一解或无解)
已知两个分力的方向(唯一解)
输入你的标题
详细内容……点击输入本栏的具体文字,简明扼要的说明分项内容。
已知一个分力的大小方向(唯一解)
DECOMPOSITION OF THE FORCE
第三章:相互作用
新课引入
1、在作用效果相同的情况下,几个力可以用一个力来替代。问:在作用效果相同的情况下,一个力能否用几个力来替代呢?
复习:力的合成
F1
F2
F
力的合成遵循平行四边形定则
求一个力的分力的过程,叫力的分解
力的分解是力的合成的逆运算,同样遵循平行四边形定则
力可以合成,
是否也可以分解?
如果不加限制条件,一个力可分解为无数组不同的分力
思 考
不加限制的条件下,一个力可分解为无数组不同的分力。
那么实际处理力的分解时又该如何进行呢?
力的分解
F2= F sinθ
θ
F
F1
F2
F1= F cosθ
已知放在水平面上的物体,受到与水平方向成θ角的拉力F 的作用
对物体的斜向上的拉力F 会产生怎样的作用效果?如何分解?
力的分解
θ
放在斜面上的物体所受重力G产生怎样的作用效果?如何分解?
G
F1= G sinθ
F2
F1
下滑力(重力的一个分力)
θ
F2= G cosθ
当θ增大时,F1、F2如何变化?
已知放在斜面上的物体所受重力为G,斜面倾角为θ
实例分析
思考题
1 当斜面倾角θ增大时分析F1和F2如何变化?
2 当倾角θ减少时,F1和F2如何变化?
当θ增大时,F1增大,F2减小。
当θ减小时,F1减小,F2增大。
斜面上物体的重力的分解是否是惟一?
思考题
要使一个力的分解是惟一的,对两分力有什么要求?
①已知两个分力的方向(不在同一直线上)
②已知一个分力的大小和方向
力的分解
二、矢量相加的法则
1、平行四边形定则在位移运算中的应用
人从A到B,再到C的过程中,总位移与两段位移的关系。
A
B
C
X1
X2
X
力的分解
2、三角形定则
把两个矢量首尾连接求出合矢量的方法。
三角形定则与平行四边形定则实质一样.
C
B
A
两个矢量首尾相接,从第一个矢量的始端指向第二个矢量的末端的有向线段就表示合矢量的大小和方向.
力的分解
F1
F2
F
F4
F3
F1
F2
F4
F3
力的分解
一个物体的速度V1在一小段时间内发生了变化,变成了V2,你能根据三角形定则找出变化量ΔV吗?
3、矢量和标量
矢量:有大小,又有方向,相加时遵循平行四边形定则
标量:有大小,没有方向,求和时按算术法则相加
V1
V2
ΔV
说一说
力的分解
F1= G cosθ
F2= G sinθ
悬挂着的物体所受重力G产生怎样的作用效果?如何分解?
θ
F1
F2
G
θ
A
B
O
用两根轻绳将物体悬挂起来。已知物体重力为G,轻绳AO与水平方向夹角为θ,AOB为直角
分解力的步骤
1、分析力的作用效果。
2、根据力的作用效果确定分力的方向。
输入3、由平行四边形定则确定分力的大小。你的标题
力的分解
θ
F2= G cosθ
G
F1
F2
θ
θ
F1
F2
G
θ
F1= G sinθ
F1= G tanθ
F2= G/cosθ
放在斜面上的物体所受重力G产生怎样的作用效果?如何分解?
力的分解
F1= F /sinθ
F2= F cotθ
A
B
C
θ
F
F1
θ
A
B
C
θ
F
F1
θ
F2
F1= F cotθ
F2= F /sinθ
F2
作用在三角支架上的力F 的作用效果怎样?如何分解?
可自由转动的轻杆AC 和BC ,BC 杆水平。在它们的连接处C点施加一个竖直向下的力F
力的分解
3、如图所示,质量为m的木块在力F作用下在水平面上做匀速运动。木块与地面间的动摩擦因数为?,则物体受到的摩擦力为( )
?
F
?mg
?(mg+Fsin?)
?(mg-Fsin?)
Fcos?
B、D
力的分解的解的个数
F大小、方向
F1大小、方向
F2大小、方向
1.已知合力和两个分力的方向
唯一解
2.已知合力和一个分力的大小和方向
唯一解
3.已知合力和两个分力的大小
两组解
(F1+F2>F且F1≠F2)
(F1、F2不在同一直线上)
若(F1+F2>F且F1=F2) 一组解
力的分解
4.已知合力F及一个分力F2的大小和另一个分力F1的方向 (F1与F的夹角为θ)
①当F2
③当Fsinθ
θ为锐角时:
θ为钝角时:
①当F2≤F时,无解 ②当F2>F时,一组解
课堂小结
一、原则:根据力的实际作用效果分解
二、方法:平行四边形定则(解三角形)
02
01
03
04
已知一个分力的方向和另一个分力的大小 (两解、一解或无解)
已知两个分力的方向(唯一解)
输入你的标题
详细内容……点击输入本栏的具体文字,简明扼要的说明分项内容。
已知一个分力的大小方向(唯一解)
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
