人教版九年级数学上册寒假讲义 第三讲 二次函数(含答案)
文档属性
| 名称 | 人教版九年级数学上册寒假讲义 第三讲 二次函数(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 344.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-12 22:13:10 | ||
图片预览



文档简介
2021年寒假班九年级数学教案
第二讲
二次函数的图像和性质
第三讲
二次函数系数相关
知识点1:二次函数的图象与系数的关系
1、a的符号:由抛物线的开口方向决定.开口向上,则a>0;开口向下,则a<0.
2、b的符号:由对称轴和a的符号决定,若对称轴是y轴,则b=0;若对称轴在y轴左侧,顶点的横坐标-<0,即>0,则a、b为同号;若对称轴在y轴右侧,顶点的横坐标->0,即<0.则a、b异号.
“左同右异”.
3.c的符号:由抛物线与y轴的交点位置确定.若抛物线交y轴于正半,则c>0,抛物线交y轴于负半轴.则c<0;若抛物线过原点,则c=0.
4.△的符号:△的符号由抛物线与x轴的交点个数决定.若抛物线与x轴只有一个交点,则△=0;有两个交点,则△>0.没有交点,则△<0
.
5、a+b+c与a-b+c的符号:根据x=1或x=-1时,y对应的值的符号确定.
例1、已知二次函数的图象如图
l-2-2所示,则a、b、c满足(
)
A.a<0,b<0,c>0
B.a<0,b<0,c<0
C.a<0,b>0,c>0
D.a>0,b<0,c>0
例2、已知二次函数
(a≠0)且a<0,a-b+c>0,则一定有(
)
A.b2-4ac>0
B.b2-4ac=0
C.b2-4ac<0
D.b2-4ac≤0
例3、二次函数的图象如图1-2-10,则点(b,)在(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
例4、已知函数的图象如图1-2-11所示,给出下列关于系数a、b、c的不等式:①a<0,②b<0,③c>0,④2a+b
<0,⑤a+b+c>0.其中正确的不等式的序号为___________-
例5、已知抛物线与x轴交点的横坐标为-1,则a+c=_________.
例6、抛物线中,已知a:b:c=l:2:3,最小值为6,则此抛物线的解析式为____________
例7、抛物线如图1-2-12
所示,则它关于y轴对称的抛物线的解析式是___________.
例8、若抛物线过点(1,0)且其解析式中二次项系数为1,则它的解析式为___________.(任写一个)
例9、已知二次函数的图象与x轴交于点(-2,0),(x1,0)且1<x1<2,与y·轴正半轴的交点连点(0,2)的下方,下列结论:①a<b<0;②2a+c>0;③4a+c<
0,④2a-b+l>0.其中的有正确的结论是(填写序号)__________.
知识点2:二次函数解析式求法
1.二次函数的三种表示方法:
⑴表格法:可以清楚、直接地表示出变量之间的数值对应关系;
⑵图象法:可以直观地表示出函数的变化过程和变化趋势;
⑶表达式:可以比较全面、完整、简洁地表示出变量之间的关系.
2.二次函数表达式的求法:
⑴一般式法:若已知抛物线上三点坐标,可利用待定系数法求得;将已知的三个点的坐标分别代入解析式,得到一个三元一次方程组,解这个方程组即可。
⑵顶点式法:若已知抛物线的顶点坐标或对称轴方程,则可采用顶点式:其中顶点为(h,k),对称轴为直线x=h;
⑶交点式法:若已知抛物线与x轴的交点坐标或交点的横坐标,则可采用交点式:,其中与x轴的交点坐标为(x1,0),(x2,0)。
解题小诀窍:在求二次函数解析式时,要灵活根据题目给出的条件来设解析式。例如,已知二次函数的顶点在坐标原点可设;已知顶点(0,c),即在y轴上时可设;已知顶点(h,0)即顶点在x轴上可设.
注意:当涉及面积周长的问题时,一定要注意自变量的取值范围。
例10、已知抛物线的对称轴为x=2,且经过点(0,4)和点(5,0),则该抛物线解析式为__________.
例11、若函数y=a(x-h)2+k的图象经过原点,最小值为8,且形状与抛物线y=-2x2-2x+3相同,则此函数关系式______.
例12、在直角坐标系中,△AOB的顶点坐标分别为A(0,2),O(0,0),B(4,0),把△AOB绕O点按逆时针方向旋转900到△COD。
(1)求C,D两点的坐标;
(2)求经过C,D,B三点的抛物线解析式。
例13、如图,抛物线的对称轴是直线x=1,它与x轴交于A,B两点,与y轴交于C点。点A,C的坐标分别是(-1,0),(0,)。
(1)求此抛物线对应的函数解析式;
(2)若点P是抛物线上位于x轴上方的一个动点,求△ABP的面积的最大值。
例14、在ΔABC中,∠ABC=90○
,点C在x轴正半轴上,点A在x轴负半轴上,点B在y轴正半轴上(图1-2-26所示),若
tan∠BAC=
,OB=2,求经过
A、B、C点的抛物线的解析式.
例15、已知:如图1-2-27所示,直线y=-x+3与x
轴、y轴分别交于点B、C,抛物线y=-x2+bx+c经过点B、C,点A是抛物线与x轴的另一个交点.
(1)求抛物线的解析式;
(2)若点P在直线BC上,且SΔPAC=SΔPAB,求点P的坐标.
综合训练三
选择题:
1、抛物线的对称轴是(
)
A.
直线
B.
直线
C.
直线
D.
直线
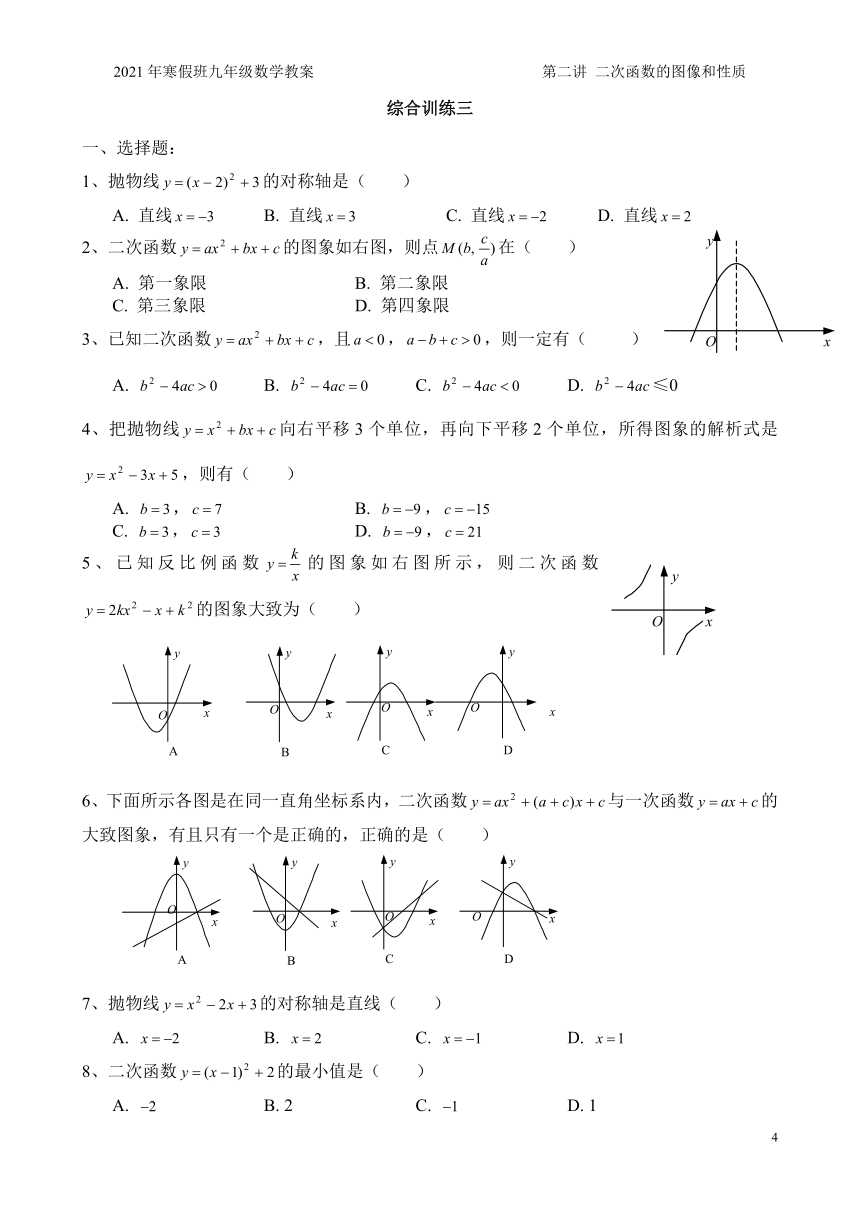
2、二次函数的图象如右图,则点在(
)
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
3、已知二次函数,且,,则一定有(
)
A.
B.
C.
D.
≤0
4、把抛物线向右平移3个单位,再向下平移2个单位,所得图象的解析式是,则有(
)
A.
,
B.
,
C.
,
D.
,
5、已知反比例函数的图象如右图所示,则二次函数的图象大致为(
)
6、下面所示各图是在同一直角坐标系内,二次函数与一次函数的大致图象,有且只有一个是正确的,正确的是(
)
7、抛物线的对称轴是直线(
)
A.
B.
C.
D.
8、二次函数的最小值是(
)
A.
B.
2
C.
D.
1
9、二次函数的图象如图所示,若
,,则(
)
A.
,,
B.
,,
C.
,,
D.
,,
二、填空题:
将二次函数配方成的形式,则y=______________________.
10、有一个二次函数的图象,三位同学分别说出它的一些特点:
甲:对称轴是直线;
乙:与x轴两个交点的横坐标都是整数;
丙:与y轴交点的纵坐标也是整数,且以这三个交点为顶点的三角形面积为3.
请你写出满足上述全部特点的一个二次函数解析式:
11、已知二次函数的图象开口向上,且与y轴的正半轴相交,请你写出一个满足条件的二次函数的解析式:_____________________.
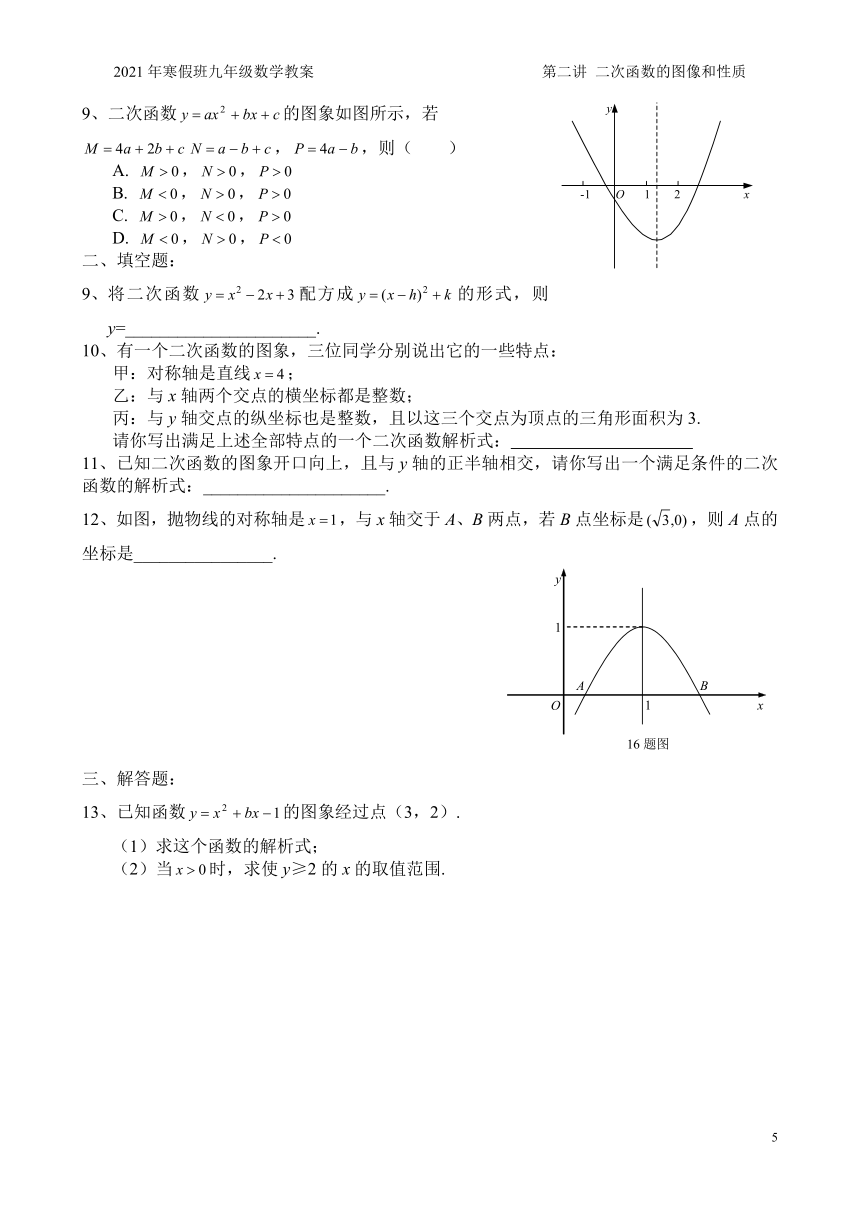
12、如图,抛物线的对称轴是,与x轴交于A、B两点,若B点坐标是,则A点的坐标是________________.
三、解答题:
13、已知函数的图象经过点(3,2).
(1)求这个函数的解析式;
(2)当时,求使y≥2的x的取值范围.
14、如右图,抛物线经过点,与y轴交于点B.
(1)求抛物线的解析式;
(2)P是y轴正半轴上一点,且△PAB是以AB为腰的等腰三角形,试求点P的坐标.
15、某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到赢利的过程,下面的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).
(1)由已知图象上的三点坐标,求累积利润s(万元)与销售时间t(月)之间的函数关系式;
(2)求截止到几月累积利润可达到30万元;
求第8个月公司所获利润是多少万元?
16、卢浦大桥拱形可以近似地看作抛物线的一部分.
在大桥截面1:11000的比例图上去,跨度AB=5cm,拱高OC=0.9cm,线段DE表示大桥拱内桥长,DE∥AB,如图(1).
在比例图上,以直线AB为x轴,抛物线的对称轴为y轴,以1cm作为数轴的单位长度,建立平面直角坐标系,如图(2).
(1)求出图(2)上以这一部分抛物线为图象的函数解析式,写出函数定义域;
(2)如果DE与AB的距离OM=0.45cm,求卢浦大桥拱内实际桥长(备用数据:≈1.4,计算结果精确到1米).
17、已知二次函数的图象交x轴于、两点,,交y轴的负半轴与C点,且AB=3,tan∠BAC=
tan∠ABC=1.
(1)求此二次函数的解析式;
(2)在第一象限,抛物线上是否存在点P,使S△PAB=6?若存在,请你求出点P的坐标;若不存在,请你说明理由.
18、已知抛物线与x轴只有一个交点,且交点为.
(1)求b、c的值;
(2)若抛物线与y轴的交点为B,坐标原点为O,求△OAB的周长与面积(答案可带根号).
参考答案
一、选择题:
题号
1
2
3
4
5
6
7
8
9
答案
D
D
A
A
D
D
D
B
D
二、填空题:
1.
2.
有两个不相等的实数根
3.
1
4.
(1)图象都是抛物线;(2)开口向上;(3)都有最低点(或最小值)
5.
或或或
6.
等(只须,)
7.
8.
,,1,4
三、解答题:
1.
解:(1)∵函数的图象经过点(3,2),∴.
解得.
∴函数解析式为.
(2)当时,.
根据图象知当x≥3时,y≥2.
∴当时,使y≥2的x的取值范围是x≥3.
2.
解:(1)由题意得.
∴.
∴抛物线的解析式为.
(2)∵点A的坐标为(1,0),点B的坐标为.
∴OA=1,OB=4.
在Rt△OAB中,,且点P在y轴正半轴上.
①当PB=PA时,.
∴.
此时点P的坐标为.
②当PA=AB时,OP=OB=4
此时点P的坐标为(0,4).
3.
解:(1)设s与t的函数关系式为,
由题意得或
解得
∴.
(2)把s=30代入,得
解得,(舍去)
答:截止到10月末公司累积利润可达到30万元.
(3)把代入,得
把代入,得
.
答:第8个月获利润5.5万元.
4.
解:(1)由于顶点在y轴上,所以设这部分抛物线为图象的函数的解析式为.
因为点或在抛物线上,所以,得.
因此所求函数解析式为(≤x≤).
(2)因为点D、E的纵坐标为,所以,得.
所以点D的坐标为,点E的坐标为.
所以.
因此卢浦大桥拱内实际桥长为(米).
5.
解:(1)∵AB=3,,∴.
由根与系数的关系有.
∴,.
∴OA=1,OB=2,.
∵,∴.
∴OC=2.
∴,.
∴此二次函数的解析式为.
(2)在第一象限,抛物线上存在一点P,使S△PAC=6.
解法一:过点P作直线MN∥AC,交x轴于点M,交y轴于N,连结PA、PC、MC、NA.
∵MN∥AC,∴S△MAC=S△NAC=
S△PAC=6.
由(1)有OA=1,OC=2.
∴.
∴AM=6,CN=12.
∴M(5,0),N(0,10).
∴直线MN的解析式为.
由
得(舍去)
∴在
第一象限,抛物线上存在点,使S△PAC=6.
解法二:设AP与y轴交于点(m>0)
∴直线AP的解析式为.
∴.
∴,∴.
又S△PAC=
S△ADC+
S△PDC==.
∴,
∴(舍去)或.
∴在
第一象限,抛物线上存在点,使S△PAC=6.
1.
解:(1)∵抛物线与x轴只有一个交点,
∴方程有两个相等的实数根,即.
①
又点A的坐标为(2,0),∴.
②
由①②得,.
(2)由(1)得抛物线的解析式为.
当时,.
∴点B的坐标为(0,4).
在Rt△OAB中,OA=2,OB=4,得.
∴△OAB的周长为.
第二讲
二次函数的图像和性质
第三讲
二次函数系数相关
知识点1:二次函数的图象与系数的关系
1、a的符号:由抛物线的开口方向决定.开口向上,则a>0;开口向下,则a<0.
2、b的符号:由对称轴和a的符号决定,若对称轴是y轴,则b=0;若对称轴在y轴左侧,顶点的横坐标-<0,即>0,则a、b为同号;若对称轴在y轴右侧,顶点的横坐标->0,即<0.则a、b异号.
“左同右异”.
3.c的符号:由抛物线与y轴的交点位置确定.若抛物线交y轴于正半,则c>0,抛物线交y轴于负半轴.则c<0;若抛物线过原点,则c=0.
4.△的符号:△的符号由抛物线与x轴的交点个数决定.若抛物线与x轴只有一个交点,则△=0;有两个交点,则△>0.没有交点,则△<0
.
5、a+b+c与a-b+c的符号:根据x=1或x=-1时,y对应的值的符号确定.
例1、已知二次函数的图象如图
l-2-2所示,则a、b、c满足(
)
A.a<0,b<0,c>0
B.a<0,b<0,c<0
C.a<0,b>0,c>0
D.a>0,b<0,c>0
例2、已知二次函数
(a≠0)且a<0,a-b+c>0,则一定有(
)
A.b2-4ac>0
B.b2-4ac=0
C.b2-4ac<0
D.b2-4ac≤0
例3、二次函数的图象如图1-2-10,则点(b,)在(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
例4、已知函数的图象如图1-2-11所示,给出下列关于系数a、b、c的不等式:①a<0,②b<0,③c>0,④2a+b
<0,⑤a+b+c>0.其中正确的不等式的序号为___________-
例5、已知抛物线与x轴交点的横坐标为-1,则a+c=_________.
例6、抛物线中,已知a:b:c=l:2:3,最小值为6,则此抛物线的解析式为____________
例7、抛物线如图1-2-12
所示,则它关于y轴对称的抛物线的解析式是___________.
例8、若抛物线过点(1,0)且其解析式中二次项系数为1,则它的解析式为___________.(任写一个)
例9、已知二次函数的图象与x轴交于点(-2,0),(x1,0)且1<x1<2,与y·轴正半轴的交点连点(0,2)的下方,下列结论:①a<b<0;②2a+c>0;③4a+c<
0,④2a-b+l>0.其中的有正确的结论是(填写序号)__________.
知识点2:二次函数解析式求法
1.二次函数的三种表示方法:
⑴表格法:可以清楚、直接地表示出变量之间的数值对应关系;
⑵图象法:可以直观地表示出函数的变化过程和变化趋势;
⑶表达式:可以比较全面、完整、简洁地表示出变量之间的关系.
2.二次函数表达式的求法:
⑴一般式法:若已知抛物线上三点坐标,可利用待定系数法求得;将已知的三个点的坐标分别代入解析式,得到一个三元一次方程组,解这个方程组即可。
⑵顶点式法:若已知抛物线的顶点坐标或对称轴方程,则可采用顶点式:其中顶点为(h,k),对称轴为直线x=h;
⑶交点式法:若已知抛物线与x轴的交点坐标或交点的横坐标,则可采用交点式:,其中与x轴的交点坐标为(x1,0),(x2,0)。
解题小诀窍:在求二次函数解析式时,要灵活根据题目给出的条件来设解析式。例如,已知二次函数的顶点在坐标原点可设;已知顶点(0,c),即在y轴上时可设;已知顶点(h,0)即顶点在x轴上可设.
注意:当涉及面积周长的问题时,一定要注意自变量的取值范围。
例10、已知抛物线的对称轴为x=2,且经过点(0,4)和点(5,0),则该抛物线解析式为__________.
例11、若函数y=a(x-h)2+k的图象经过原点,最小值为8,且形状与抛物线y=-2x2-2x+3相同,则此函数关系式______.
例12、在直角坐标系中,△AOB的顶点坐标分别为A(0,2),O(0,0),B(4,0),把△AOB绕O点按逆时针方向旋转900到△COD。
(1)求C,D两点的坐标;
(2)求经过C,D,B三点的抛物线解析式。
例13、如图,抛物线的对称轴是直线x=1,它与x轴交于A,B两点,与y轴交于C点。点A,C的坐标分别是(-1,0),(0,)。
(1)求此抛物线对应的函数解析式;
(2)若点P是抛物线上位于x轴上方的一个动点,求△ABP的面积的最大值。
例14、在ΔABC中,∠ABC=90○
,点C在x轴正半轴上,点A在x轴负半轴上,点B在y轴正半轴上(图1-2-26所示),若
tan∠BAC=
,OB=2,求经过
A、B、C点的抛物线的解析式.
例15、已知:如图1-2-27所示,直线y=-x+3与x
轴、y轴分别交于点B、C,抛物线y=-x2+bx+c经过点B、C,点A是抛物线与x轴的另一个交点.
(1)求抛物线的解析式;
(2)若点P在直线BC上,且SΔPAC=SΔPAB,求点P的坐标.
综合训练三
选择题:
1、抛物线的对称轴是(
)
A.
直线
B.
直线
C.
直线
D.
直线
2、二次函数的图象如右图,则点在(
)
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
3、已知二次函数,且,,则一定有(
)
A.
B.
C.
D.
≤0
4、把抛物线向右平移3个单位,再向下平移2个单位,所得图象的解析式是,则有(
)
A.
,
B.
,
C.
,
D.
,
5、已知反比例函数的图象如右图所示,则二次函数的图象大致为(
)
6、下面所示各图是在同一直角坐标系内,二次函数与一次函数的大致图象,有且只有一个是正确的,正确的是(
)
7、抛物线的对称轴是直线(
)
A.
B.
C.
D.
8、二次函数的最小值是(
)
A.
B.
2
C.
D.
1
9、二次函数的图象如图所示,若
,,则(
)
A.
,,
B.
,,
C.
,,
D.
,,
二、填空题:
将二次函数配方成的形式,则y=______________________.
10、有一个二次函数的图象,三位同学分别说出它的一些特点:
甲:对称轴是直线;
乙:与x轴两个交点的横坐标都是整数;
丙:与y轴交点的纵坐标也是整数,且以这三个交点为顶点的三角形面积为3.
请你写出满足上述全部特点的一个二次函数解析式:
11、已知二次函数的图象开口向上,且与y轴的正半轴相交,请你写出一个满足条件的二次函数的解析式:_____________________.
12、如图,抛物线的对称轴是,与x轴交于A、B两点,若B点坐标是,则A点的坐标是________________.
三、解答题:
13、已知函数的图象经过点(3,2).
(1)求这个函数的解析式;
(2)当时,求使y≥2的x的取值范围.
14、如右图,抛物线经过点,与y轴交于点B.
(1)求抛物线的解析式;
(2)P是y轴正半轴上一点,且△PAB是以AB为腰的等腰三角形,试求点P的坐标.
15、某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到赢利的过程,下面的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).
(1)由已知图象上的三点坐标,求累积利润s(万元)与销售时间t(月)之间的函数关系式;
(2)求截止到几月累积利润可达到30万元;
求第8个月公司所获利润是多少万元?
16、卢浦大桥拱形可以近似地看作抛物线的一部分.
在大桥截面1:11000的比例图上去,跨度AB=5cm,拱高OC=0.9cm,线段DE表示大桥拱内桥长,DE∥AB,如图(1).
在比例图上,以直线AB为x轴,抛物线的对称轴为y轴,以1cm作为数轴的单位长度,建立平面直角坐标系,如图(2).
(1)求出图(2)上以这一部分抛物线为图象的函数解析式,写出函数定义域;
(2)如果DE与AB的距离OM=0.45cm,求卢浦大桥拱内实际桥长(备用数据:≈1.4,计算结果精确到1米).
17、已知二次函数的图象交x轴于、两点,,交y轴的负半轴与C点,且AB=3,tan∠BAC=
tan∠ABC=1.
(1)求此二次函数的解析式;
(2)在第一象限,抛物线上是否存在点P,使S△PAB=6?若存在,请你求出点P的坐标;若不存在,请你说明理由.
18、已知抛物线与x轴只有一个交点,且交点为.
(1)求b、c的值;
(2)若抛物线与y轴的交点为B,坐标原点为O,求△OAB的周长与面积(答案可带根号).
参考答案
一、选择题:
题号
1
2
3
4
5
6
7
8
9
答案
D
D
A
A
D
D
D
B
D
二、填空题:
1.
2.
有两个不相等的实数根
3.
1
4.
(1)图象都是抛物线;(2)开口向上;(3)都有最低点(或最小值)
5.
或或或
6.
等(只须,)
7.
8.
,,1,4
三、解答题:
1.
解:(1)∵函数的图象经过点(3,2),∴.
解得.
∴函数解析式为.
(2)当时,.
根据图象知当x≥3时,y≥2.
∴当时,使y≥2的x的取值范围是x≥3.
2.
解:(1)由题意得.
∴.
∴抛物线的解析式为.
(2)∵点A的坐标为(1,0),点B的坐标为.
∴OA=1,OB=4.
在Rt△OAB中,,且点P在y轴正半轴上.
①当PB=PA时,.
∴.
此时点P的坐标为.
②当PA=AB时,OP=OB=4
此时点P的坐标为(0,4).
3.
解:(1)设s与t的函数关系式为,
由题意得或
解得
∴.
(2)把s=30代入,得
解得,(舍去)
答:截止到10月末公司累积利润可达到30万元.
(3)把代入,得
把代入,得
.
答:第8个月获利润5.5万元.
4.
解:(1)由于顶点在y轴上,所以设这部分抛物线为图象的函数的解析式为.
因为点或在抛物线上,所以,得.
因此所求函数解析式为(≤x≤).
(2)因为点D、E的纵坐标为,所以,得.
所以点D的坐标为,点E的坐标为.
所以.
因此卢浦大桥拱内实际桥长为(米).
5.
解:(1)∵AB=3,,∴.
由根与系数的关系有.
∴,.
∴OA=1,OB=2,.
∵,∴.
∴OC=2.
∴,.
∴此二次函数的解析式为.
(2)在第一象限,抛物线上存在一点P,使S△PAC=6.
解法一:过点P作直线MN∥AC,交x轴于点M,交y轴于N,连结PA、PC、MC、NA.
∵MN∥AC,∴S△MAC=S△NAC=
S△PAC=6.
由(1)有OA=1,OC=2.
∴.
∴AM=6,CN=12.
∴M(5,0),N(0,10).
∴直线MN的解析式为.
由
得(舍去)
∴在
第一象限,抛物线上存在点,使S△PAC=6.
解法二:设AP与y轴交于点(m>0)
∴直线AP的解析式为.
∴.
∴,∴.
又S△PAC=
S△ADC+
S△PDC==.
∴,
∴(舍去)或.
∴在
第一象限,抛物线上存在点,使S△PAC=6.
1.
解:(1)∵抛物线与x轴只有一个交点,
∴方程有两个相等的实数根,即.
①
又点A的坐标为(2,0),∴.
②
由①②得,.
(2)由(1)得抛物线的解析式为.
当时,.
∴点B的坐标为(0,4).
在Rt△OAB中,OA=2,OB=4,得.
∴△OAB的周长为.
同课章节目录
