人教版七年级数学下册 5.1 相交线 同步测试题(word版含解析)
文档属性
| 名称 | 人教版七年级数学下册 5.1 相交线 同步测试题(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 123.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-11 00:17:58 | ||
图片预览

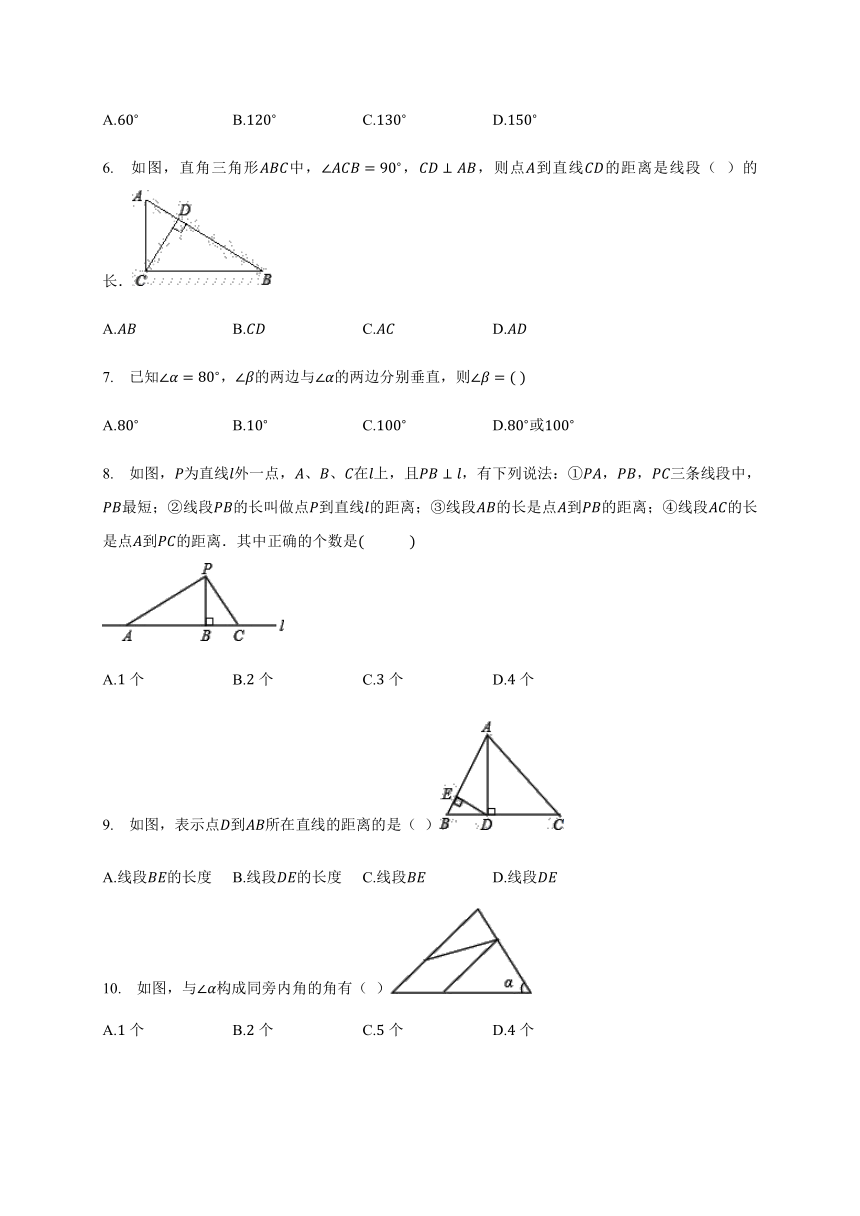
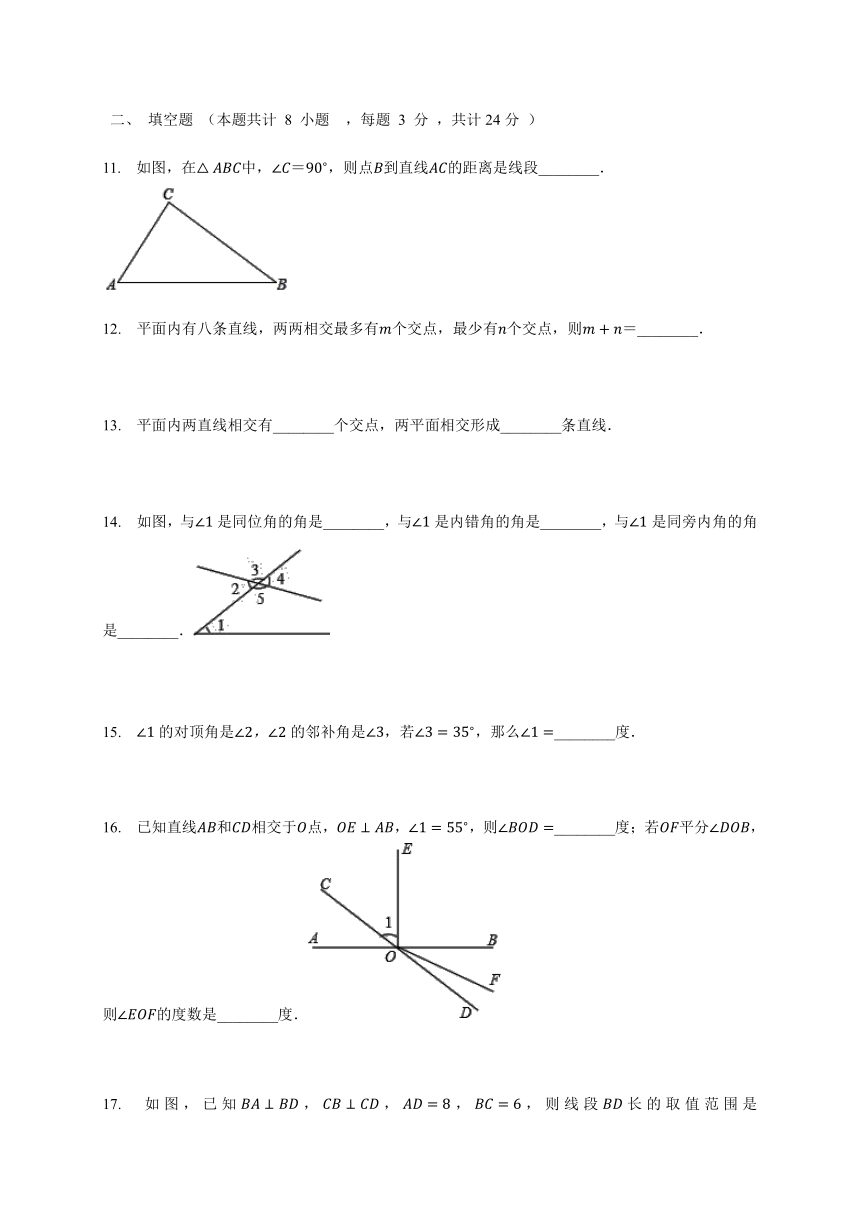
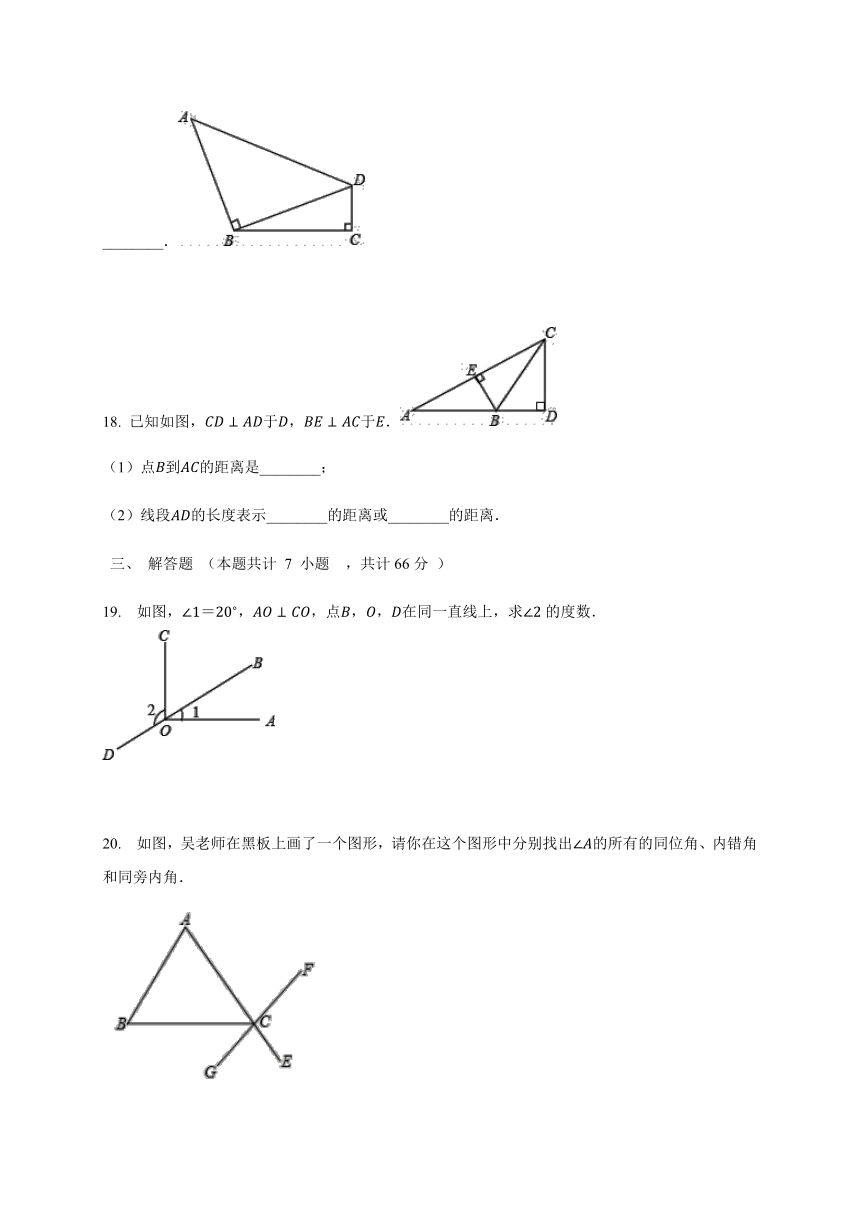
文档简介
5.1
相交线
同步测试题
班级:_____________姓名:_____________
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
?1.
在一个平面内,任意三条直线相交,交点的个数最多有(
)
A.个
B.个
C.个
D.个
?2.
的对顶角是,的邻补角是,若,则的度数是(????????)
A.
B.
C.
D.或
?3.
如图,,=,点是线段上的动点,则、两点之间的距离不可能是(
)
A.
B.
C.
D.?
4.
如图,直线,相交于点,且,若,则的度数是?
?
?
?
A.
B.
C.
D.
5.
如图,直线,相交于点,,垂足为,若,则的大小是(?
?
?
?
)
A.
B.
C.
D.?
6.
如图,直角三角形中,,,则点到直线的距离是线段(
)的长.
A.
B.
C.
D.?
7.
已知,的两边与的两边分别垂直,则
A.
B.
C.
D.或?
8.
如图,为直线外一点,、、在上,且,有下列说法:①,,三条线段中,最短;②线段的长叫做点到直线的距离;③线段的长是点到的距离;④线段的长是点到的距离.其中正确的个数是?
?
?
?
A.个
B.个
C.个
D.个?
9.
如图,表示点到所在直线的距离的是(
)
A.线段的长度
B.线段的长度
C.线段
D.线段?
10.
如图,与构成同旁内角的角有(
)
A.个
B.个
C.个
D.个
二、
填空题
(本题共计
8
小题
,每题
3
分
,共计24分
)
?
11.
如图,在中,=,则点到直线的距离是线段________.
?
12.
平面内有八条直线,两两相交最多有个交点,最少有个交点,则=________.
?
13.
平面内两直线相交有________个交点,两平面相交形成________条直线.
?
14.
如图,与是同位角的角是________,与是内错角的角是________,与是同旁内角的角是________.
?
15.
?的对顶角是的邻补角是,若,那么________度.
?
16.
已知直线和相交于点,,,则________度;若平分,则的度数是________度.
?
17.
如图,已知,,,,则线段长的取值范围是________.
?
18.
已知如图,于,于.
(1)点到的距离是________;
(2)线段的长度表示________的距离或________的距离.
三、
解答题
(本题共计
7
小题
,共计66分
)
?
19.
如图,=,,点,,在同一直线上,求的度数.
?
20.
如图,吴老师在黑板上画了一个图形,请你在这个图形中分别找出的所有的同位角、内错角和同旁内角.
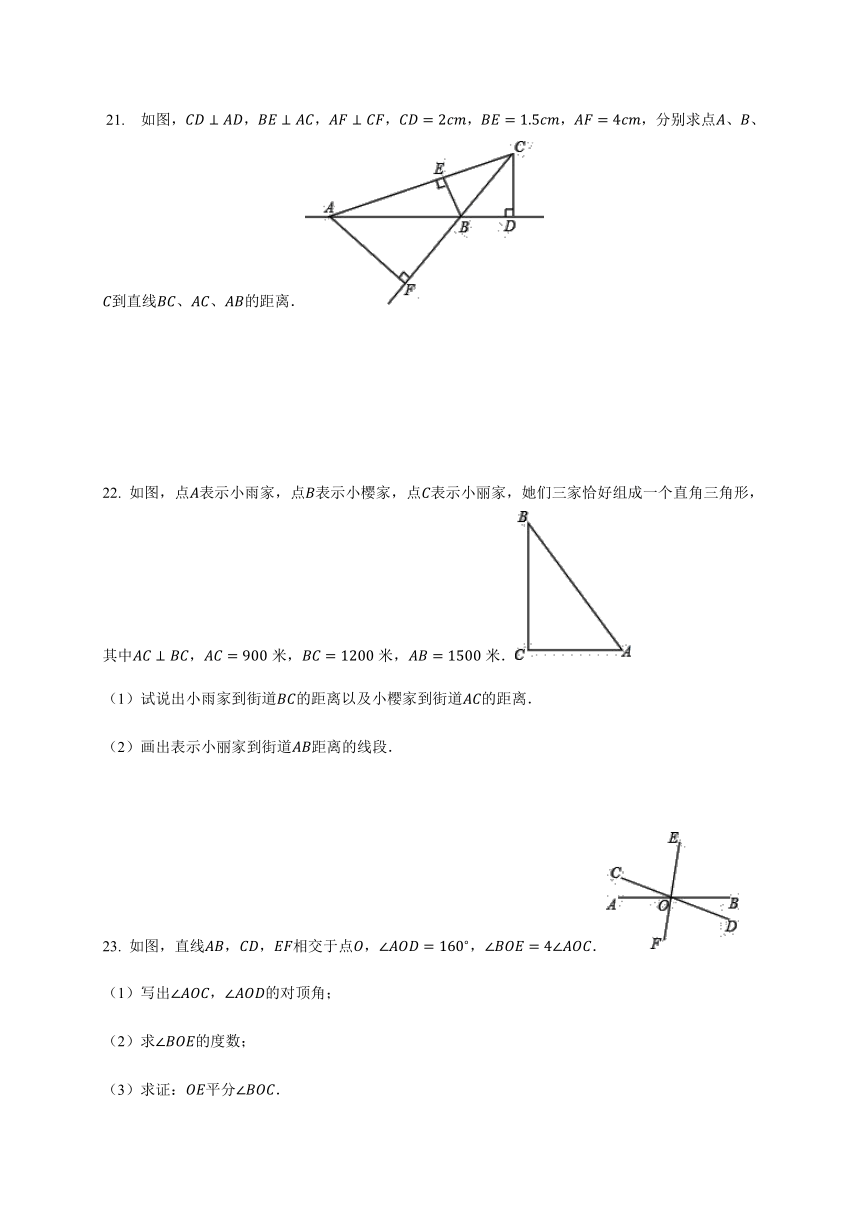
?21.
如图,,,,,,,分别求点、、到直线、、的距离.
?
22.
如图,点表示小雨家,点表示小樱家,点表示小丽家,她们三家恰好组成一个直角三角形,其中,米,米,米.
(1)试说出小雨家到街道的距离以及小樱家到街道的距离.
(2)画出表示小丽家到街道距离的线段.
?
23.
如图,直线,,相交于点,,.
(1)写出,的对顶角;
(2)求的度数;
(3)求证:平分.
?24.
如图,直线,相交于点,,垂足为,,求的度数.
?
25.
同一平面内条直线把平面分成两个部分(或区域);条直线最多可将平面分成几个部分?条直线最多可将平面分成几个部分?条直线最多可将平面分成几个部分?请分别画出图来.由此可知条直线最多可将平面分成几个部分?
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
D
【解答】
解:三条直线相交时,位置关系如图所示:
判断可知:最多有个交点,故选.
2.
【答案】
C
【解答】
解:的对顶角是,
故,
的邻补角是,
则,
若,
则.
故选.
3.
【答案】
A
【解答】
∵
,=,
∴
,即.
观察选项,只有选项符合题意.
4.
【答案】
B
【解答】
解:
,
故选
5.
【答案】
B
【解答】
解:∵
直线,相交于点,
∴
.
∵
,
∴
,
∴
.
故选.
6.
【答案】
D
【解答】
解:点到直线的距离就是过点作直线的垂线,其垂线段的长度可表示距离.故选.
7.
【答案】
D
【解答】
解:∵
的两边与的两边分别垂直,
∴
,
故,
在上述情况下,若反向延长的一边,那么的补角的两边也与的两边互相垂直,故此时;
综上可知:或,
故选:.
8.
【答案】
C
【解答】
解:①为垂线段,长度最短,正确;
②线段的长叫做点到直线的距离,是定义,正确;
③线段的长是点到的距离,根据“从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离”,符合点到直线距离的定义,正确;
④线段的长是点到的距离,不符合点到直线距离的定义,错误.
故选.
9.
【答案】
B
【解答】
解:由题意得表示点到所在直线的距离的是线段的长度,
故选:.
10.
【答案】
C
【解答】
解:根据同旁内角的定义可知:与构成同旁内角的角有个.故选.
二、
填空题
(本题共计
8
小题
,每题
3
分
,共计24分
)
11.
【答案】
【解答】
如图,三角形中,=,则点到直线的距离是:线段.
12.
【答案】
【解答】
根据题意可得:条直线相交于一点时交点最少,此时交点为个,
即=;
任意两直线相交都产生一个交点时,交点最多,
∴
此时交点为:=,
即=;
则==.
13.
【答案】
,
【解答】
解:在同一平面内,直线相交有只能有一个交点,而平面相交则是一条直线,且只有一条.
14.
【答案】
,,
【解答】
解:与是同位角的角是,与是内错角的角是,与是同旁内角的角是,
故答案为:,,.
15.
【答案】
.
【解答】
解:已知∠的对顶角是∠,
∠的邻补角是∠,
若∠°,
则∠°∠°
∴
∠°,
故答案为.
16.
【答案】
,
【解答】
解:∵
,,
∴
,
又∵
,
∴
;
∵
,
∴
,
又∵
平分,
∴
,
.
故答案分别为:;.
17.
【答案】
【解答】
解:∵
,
∴
,
∵
,
∴
,
∵
,,
∴
线段长的取值范围是;
故答案为:.
18.
【答案】
线段的长度
、两点间,点到
【解答】
解:(1)∵
于,
∴
点到的距离是线段的长度.
(2)∵
,
∴
线段的长度表示、两点间的距离或点到.
三、
解答题
(本题共计
7
小题
,每题
10
分
,共计70分
)
19.
【答案】
∵
,
∴
=,
∵
=,
∴
==,
∴
==.
【解答】
∵
,
∴
=,
∵
=,
∴
==,
∴
==.
20.
【答案】
解:的同位角是:.
的内错角是:.
的同旁内角是:
【解答】
解:的同位角是:.
的内错角是:.
的同旁内角是:
21.
【答案】
解:点到直线的距离为垂线段的长度,是;
点到直线的距离为垂线段的长度,是;
点到直线的距离为垂线段的长度,是.
【解答】
解:点到直线的距离为垂线段的长度,是;
点到直线的距离为垂线段的长度,是;
点到直线的距离为垂线段的长度,是.
22.
【答案】
解:(1)∵
米,米,米,
∴
,
∴
小雨家到街道的距离为:,小樱家到街道的距离为:;
(2)如图所示:即为小丽家到街道距离.
【解答】
解:(1)∵
米,米,米,
∴
,
∴
小雨家到街道的距离为:,小樱家到街道的距离为:;
(2)如图所示:即为小丽家到街道距离.
23.
【答案】
(1)解:的对顶角是,的对顶角是;
(2)解:设,则,
∵
,
∴
,
解得:,
∴
;
(3)证明:∵
,
∴
,
∵
,
∴
,
∴
平分.
【解答】
(1)解:的对顶角是,的对顶角是;
(2)解:设,则,
∵
,
∴
,
解得:,
∴
;
(3)证明:∵
,
∴
,
∵
,
∴
,
∴
平分.
24.
【答案】
解:∵
,相交于点,,
∴
,
∵
,
∴
,
∴
.
【解答】
解:∵
,相交于点,,
∴
,
∵
,
∴
,
∴
.
25.
【答案】
解:条直线最多可将平面分成个部分,如图:;
三条直线最多分成可将平面分成个部分,如图:;
四条直线最多分成可将平面分成个部分,如图:;
条直线最多分成可将平面分成个部分.
【解答】
解:条直线最多可将平面分成个部分,如图:;
三条直线最多分成可将平面分成个部分,如图:;
四条直线最多分成可将平面分成个部分,如图:;
条直线最多分成可将平面分成个部分.
相交线
同步测试题
班级:_____________姓名:_____________
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
?1.
在一个平面内,任意三条直线相交,交点的个数最多有(
)
A.个
B.个
C.个
D.个
?2.
的对顶角是,的邻补角是,若,则的度数是(????????)
A.
B.
C.
D.或
?3.
如图,,=,点是线段上的动点,则、两点之间的距离不可能是(
)
A.
B.
C.
D.?
4.
如图,直线,相交于点,且,若,则的度数是?
?
?
?
A.
B.
C.
D.
5.
如图,直线,相交于点,,垂足为,若,则的大小是(?
?
?
?
)
A.
B.
C.
D.?
6.
如图,直角三角形中,,,则点到直线的距离是线段(
)的长.
A.
B.
C.
D.?
7.
已知,的两边与的两边分别垂直,则
A.
B.
C.
D.或?
8.
如图,为直线外一点,、、在上,且,有下列说法:①,,三条线段中,最短;②线段的长叫做点到直线的距离;③线段的长是点到的距离;④线段的长是点到的距离.其中正确的个数是?
?
?
?
A.个
B.个
C.个
D.个?
9.
如图,表示点到所在直线的距离的是(
)
A.线段的长度
B.线段的长度
C.线段
D.线段?
10.
如图,与构成同旁内角的角有(
)
A.个
B.个
C.个
D.个
二、
填空题
(本题共计
8
小题
,每题
3
分
,共计24分
)
?
11.
如图,在中,=,则点到直线的距离是线段________.
?
12.
平面内有八条直线,两两相交最多有个交点,最少有个交点,则=________.
?
13.
平面内两直线相交有________个交点,两平面相交形成________条直线.
?
14.
如图,与是同位角的角是________,与是内错角的角是________,与是同旁内角的角是________.
?
15.
?的对顶角是的邻补角是,若,那么________度.
?
16.
已知直线和相交于点,,,则________度;若平分,则的度数是________度.
?
17.
如图,已知,,,,则线段长的取值范围是________.
?
18.
已知如图,于,于.
(1)点到的距离是________;
(2)线段的长度表示________的距离或________的距离.
三、
解答题
(本题共计
7
小题
,共计66分
)
?
19.
如图,=,,点,,在同一直线上,求的度数.
?
20.
如图,吴老师在黑板上画了一个图形,请你在这个图形中分别找出的所有的同位角、内错角和同旁内角.
?21.
如图,,,,,,,分别求点、、到直线、、的距离.
?
22.
如图,点表示小雨家,点表示小樱家,点表示小丽家,她们三家恰好组成一个直角三角形,其中,米,米,米.
(1)试说出小雨家到街道的距离以及小樱家到街道的距离.
(2)画出表示小丽家到街道距离的线段.
?
23.
如图,直线,,相交于点,,.
(1)写出,的对顶角;
(2)求的度数;
(3)求证:平分.
?24.
如图,直线,相交于点,,垂足为,,求的度数.
?
25.
同一平面内条直线把平面分成两个部分(或区域);条直线最多可将平面分成几个部分?条直线最多可将平面分成几个部分?条直线最多可将平面分成几个部分?请分别画出图来.由此可知条直线最多可将平面分成几个部分?
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
D
【解答】
解:三条直线相交时,位置关系如图所示:
判断可知:最多有个交点,故选.
2.
【答案】
C
【解答】
解:的对顶角是,
故,
的邻补角是,
则,
若,
则.
故选.
3.
【答案】
A
【解答】
∵
,=,
∴
,即.
观察选项,只有选项符合题意.
4.
【答案】
B
【解答】
解:
,
故选
5.
【答案】
B
【解答】
解:∵
直线,相交于点,
∴
.
∵
,
∴
,
∴
.
故选.
6.
【答案】
D
【解答】
解:点到直线的距离就是过点作直线的垂线,其垂线段的长度可表示距离.故选.
7.
【答案】
D
【解答】
解:∵
的两边与的两边分别垂直,
∴
,
故,
在上述情况下,若反向延长的一边,那么的补角的两边也与的两边互相垂直,故此时;
综上可知:或,
故选:.
8.
【答案】
C
【解答】
解:①为垂线段,长度最短,正确;
②线段的长叫做点到直线的距离,是定义,正确;
③线段的长是点到的距离,根据“从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离”,符合点到直线距离的定义,正确;
④线段的长是点到的距离,不符合点到直线距离的定义,错误.
故选.
9.
【答案】
B
【解答】
解:由题意得表示点到所在直线的距离的是线段的长度,
故选:.
10.
【答案】
C
【解答】
解:根据同旁内角的定义可知:与构成同旁内角的角有个.故选.
二、
填空题
(本题共计
8
小题
,每题
3
分
,共计24分
)
11.
【答案】
【解答】
如图,三角形中,=,则点到直线的距离是:线段.
12.
【答案】
【解答】
根据题意可得:条直线相交于一点时交点最少,此时交点为个,
即=;
任意两直线相交都产生一个交点时,交点最多,
∴
此时交点为:=,
即=;
则==.
13.
【答案】
,
【解答】
解:在同一平面内,直线相交有只能有一个交点,而平面相交则是一条直线,且只有一条.
14.
【答案】
,,
【解答】
解:与是同位角的角是,与是内错角的角是,与是同旁内角的角是,
故答案为:,,.
15.
【答案】
.
【解答】
解:已知∠的对顶角是∠,
∠的邻补角是∠,
若∠°,
则∠°∠°
∴
∠°,
故答案为.
16.
【答案】
,
【解答】
解:∵
,,
∴
,
又∵
,
∴
;
∵
,
∴
,
又∵
平分,
∴
,
.
故答案分别为:;.
17.
【答案】
【解答】
解:∵
,
∴
,
∵
,
∴
,
∵
,,
∴
线段长的取值范围是;
故答案为:.
18.
【答案】
线段的长度
、两点间,点到
【解答】
解:(1)∵
于,
∴
点到的距离是线段的长度.
(2)∵
,
∴
线段的长度表示、两点间的距离或点到.
三、
解答题
(本题共计
7
小题
,每题
10
分
,共计70分
)
19.
【答案】
∵
,
∴
=,
∵
=,
∴
==,
∴
==.
【解答】
∵
,
∴
=,
∵
=,
∴
==,
∴
==.
20.
【答案】
解:的同位角是:.
的内错角是:.
的同旁内角是:
【解答】
解:的同位角是:.
的内错角是:.
的同旁内角是:
21.
【答案】
解:点到直线的距离为垂线段的长度,是;
点到直线的距离为垂线段的长度,是;
点到直线的距离为垂线段的长度,是.
【解答】
解:点到直线的距离为垂线段的长度,是;
点到直线的距离为垂线段的长度,是;
点到直线的距离为垂线段的长度,是.
22.
【答案】
解:(1)∵
米,米,米,
∴
,
∴
小雨家到街道的距离为:,小樱家到街道的距离为:;
(2)如图所示:即为小丽家到街道距离.
【解答】
解:(1)∵
米,米,米,
∴
,
∴
小雨家到街道的距离为:,小樱家到街道的距离为:;
(2)如图所示:即为小丽家到街道距离.
23.
【答案】
(1)解:的对顶角是,的对顶角是;
(2)解:设,则,
∵
,
∴
,
解得:,
∴
;
(3)证明:∵
,
∴
,
∵
,
∴
,
∴
平分.
【解答】
(1)解:的对顶角是,的对顶角是;
(2)解:设,则,
∵
,
∴
,
解得:,
∴
;
(3)证明:∵
,
∴
,
∵
,
∴
,
∴
平分.
24.
【答案】
解:∵
,相交于点,,
∴
,
∵
,
∴
,
∴
.
【解答】
解:∵
,相交于点,,
∴
,
∵
,
∴
,
∴
.
25.
【答案】
解:条直线最多可将平面分成个部分,如图:;
三条直线最多分成可将平面分成个部分,如图:;
四条直线最多分成可将平面分成个部分,如图:;
条直线最多分成可将平面分成个部分.
【解答】
解:条直线最多可将平面分成个部分,如图:;
三条直线最多分成可将平面分成个部分,如图:;
四条直线最多分成可将平面分成个部分,如图:;
条直线最多分成可将平面分成个部分.
