人教版数学九年级上册 21.1 一元二次方程 随堂练习(word版含答案)
文档属性
| 名称 | 人教版数学九年级上册 21.1 一元二次方程 随堂练习(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 471.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-12 22:18:43 | ||
图片预览



文档简介
21.1
一元二次方程
一、选择题(共12小题;共60分)
1.
关于
的方程
是一元二次方程,则
的取值范围为
A.
B.
C.
D.
2.
如果
是一元二次方程
的解,则
的值是
A.
B.
C.
D.
3.
一元二次方程
的一个根为
,则
的值为
A.
B.
C.
D.
4.
平面直角坐标系中,已知
,.若在坐标轴上取点
,使
为等腰三角形,则满足条件的点
的个数是
A.
B.
C.
D.
5.
已知
是方程
的一个实数根,则
的值是
A.
B.
C.
D.
6.
若
,则
的取值不可能是
A.
B.
C.
D.
7.
一元二次方程
的一个根为
,则
的值为
A.
B.
C.
D.
8.
若
是关于
的一元二次方程,则
的取值范围是
A.
B.
C.
D.
9.
若
是方程
的一个根,则
的值为
A.
B.
C.
D.
10.
下列方程是一元二次方程的是
A.
B.
C.
D.
11.
一个等腰三角形一边长为
,另一边长为
,那么这个等腰三角形的周长是
A.
B.
C.
或
D.
以上都不对
12.
“双
”促销活动中,小芳的妈妈计划用
元在唯品会购买价格分别为
元和
元的两种商品,则可供小芳妈妈选择的购买方案有
A.
种
B.
种
C.
种
D.
种
二、填空题(共5小题;共25分)
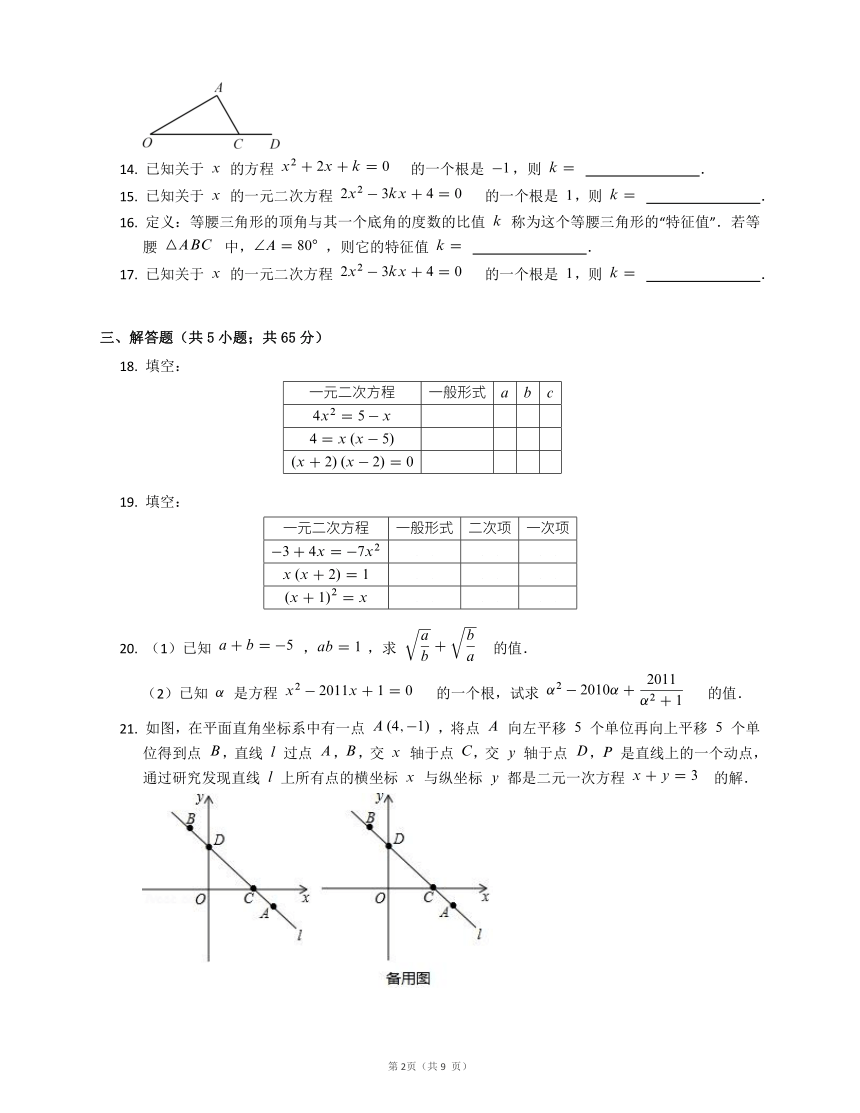
13.
如图,已知
,点
是射线
上的一个动点.在点
的运动过程中,
恰好是直角三角形,则此时
所有可能的度数为
?.
14.
已知关于
的方程
的一个根是
,则
?.
15.
已知关于
的一元二次方程
的一个根是
,则
?.
16.
定义:等腰三角形的顶角与其一个底角的度数的比值
称为这个等腰三角形的“特征值”.若等腰
中,,则它的特征值
?.
17.
已知关于
的一元二次方程
的一个根是
,则
?.
三、解答题(共5小题;共65分)
18.
填空:
19.
填空:
20.
(1)已知
,,求
的值.
(2)已知
是方程
的一个根,试求
的值.
21.
如图,在平面直角坐标系中有一点
,将点
向左平移
个单位再向上平移
个单位得到点
,直线
过点
,,交
轴于点
,交
轴于点
,
是直线上的一个动点,通过研究发现直线
上所有点的横坐标
与纵坐标
都是二元一次方程
的解.
(1)直接写出点
,,
的坐标;
?,
?,
?;
(2)求
;
(3)当
时,求点
的坐标.
22.
在平面直角坐标系
中,如果点
坐标中
,
的值是关于二元一次方程组
的解,那么称点
为该方程组的解坐标.如
是二元一次方程组
的解坐标,求:
(1)二元一次方程组
的解坐标为
?.
(2)已知方程组
与方程组
的解坐标相同,求
,
的值.
(3)当
,
满足什么条件时,关于
,
的二元一次方程组
①不存在解坐标.
②存在无数多个解坐标.
答案
第一部分
1.
C
2.
B
【解析】将
代入
,
得:,解得:.
3.
C
【解析】
一元二次方程
的一个根为
,
,解得
.
4.
A
5.
D
【解析】把
代入
,得
,
.
6.
B
【解析】分
种情况:
①两个数都是正数;
,
②两个数都是负数;
,
③其中一个数是正数另一个是负数,
.
的取值不可能是
.
7.
C
8.
A
9.
A
10.
B
11.
C
【解析】当
为等腰三角形的腰时,
三角形的三边分别是
,,
符合三角形的三边关系,
周长为
;
当
为等腰三角形的腰时,
三边分别是
,,,符合三角形的三边关系,
周长为
.
12.
A
【解析】设购买
元的商品数量为
,购买
元的商品数量为
,
依题意得:,
整理,得
是正整数,
当
时,.
当
时,.
当
时
.
当
时,.
即有
种购买方案.
第二部分
13.
或
【解析】
在
中,,
恰好是直角三角形时,分两种情况:
①如果
是直角,那么
;
②如果
是直角,那么
.
14.
15.
【解析】依题意,得
,即
,
解得
.
16.
或
【解析】①当
为顶角时,等腰三角形两底角的度数为:,
特征值
.
②当
为底角时,顶角的度数为:,
特征值
.
综上所述,特征值
为
或
.
17.
【解析】
关于
的一元二次方程
的一个根是
,
,解得
.
第三部分
18.
19.
20.
(1)
,
,
同号.
又
,
,.
??????(2)
是方程
的一个根,
,即
,.
,
.
21.
(1)
,,
【解析】
点
,将点
向左平移
个单位再向上平移
个单位得到点
,
点
直线
上所有点的横坐标
与纵坐标
都是二元一次方程
的解.
直线
的解析式为:,
当
时,,
当
时,,
点
,点
.
??????(2)
如图
,连接
,.
,
.
??????(3)
设点
,如图
.
当点
在线段
上时,
,且
,
,
,
,
,
点
.
当点
在点
的左侧时,
,且
,
,
,
,
,
点
22.
(1)
【解析】
将①
②得
将③代入②得,,,
方程组解为
解坐标为
.
??????(2)
将④
⑤得,,,
将④
⑤得,,,
将
,
代入
得,
将⑥
⑦得,,,
将⑦
⑥得,,,
??????(3)
①
若要不存在解坐标,即无解,
需要
即
②若要有无数解坐标,即有无数解,
需要
即
第1页(共1
页)
一元二次方程
一、选择题(共12小题;共60分)
1.
关于
的方程
是一元二次方程,则
的取值范围为
A.
B.
C.
D.
2.
如果
是一元二次方程
的解,则
的值是
A.
B.
C.
D.
3.
一元二次方程
的一个根为
,则
的值为
A.
B.
C.
D.
4.
平面直角坐标系中,已知
,.若在坐标轴上取点
,使
为等腰三角形,则满足条件的点
的个数是
A.
B.
C.
D.
5.
已知
是方程
的一个实数根,则
的值是
A.
B.
C.
D.
6.
若
,则
的取值不可能是
A.
B.
C.
D.
7.
一元二次方程
的一个根为
,则
的值为
A.
B.
C.
D.
8.
若
是关于
的一元二次方程,则
的取值范围是
A.
B.
C.
D.
9.
若
是方程
的一个根,则
的值为
A.
B.
C.
D.
10.
下列方程是一元二次方程的是
A.
B.
C.
D.
11.
一个等腰三角形一边长为
,另一边长为
,那么这个等腰三角形的周长是
A.
B.
C.
或
D.
以上都不对
12.
“双
”促销活动中,小芳的妈妈计划用
元在唯品会购买价格分别为
元和
元的两种商品,则可供小芳妈妈选择的购买方案有
A.
种
B.
种
C.
种
D.
种
二、填空题(共5小题;共25分)
13.
如图,已知
,点
是射线
上的一个动点.在点
的运动过程中,
恰好是直角三角形,则此时
所有可能的度数为
?.
14.
已知关于
的方程
的一个根是
,则
?.
15.
已知关于
的一元二次方程
的一个根是
,则
?.
16.
定义:等腰三角形的顶角与其一个底角的度数的比值
称为这个等腰三角形的“特征值”.若等腰
中,,则它的特征值
?.
17.
已知关于
的一元二次方程
的一个根是
,则
?.
三、解答题(共5小题;共65分)
18.
填空:
19.
填空:
20.
(1)已知
,,求
的值.
(2)已知
是方程
的一个根,试求
的值.
21.
如图,在平面直角坐标系中有一点
,将点
向左平移
个单位再向上平移
个单位得到点
,直线
过点
,,交
轴于点
,交
轴于点
,
是直线上的一个动点,通过研究发现直线
上所有点的横坐标
与纵坐标
都是二元一次方程
的解.
(1)直接写出点
,,
的坐标;
?,
?,
?;
(2)求
;
(3)当
时,求点
的坐标.
22.
在平面直角坐标系
中,如果点
坐标中
,
的值是关于二元一次方程组
的解,那么称点
为该方程组的解坐标.如
是二元一次方程组
的解坐标,求:
(1)二元一次方程组
的解坐标为
?.
(2)已知方程组
与方程组
的解坐标相同,求
,
的值.
(3)当
,
满足什么条件时,关于
,
的二元一次方程组
①不存在解坐标.
②存在无数多个解坐标.
答案
第一部分
1.
C
2.
B
【解析】将
代入
,
得:,解得:.
3.
C
【解析】
一元二次方程
的一个根为
,
,解得
.
4.
A
5.
D
【解析】把
代入
,得
,
.
6.
B
【解析】分
种情况:
①两个数都是正数;
,
②两个数都是负数;
,
③其中一个数是正数另一个是负数,
.
的取值不可能是
.
7.
C
8.
A
9.
A
10.
B
11.
C
【解析】当
为等腰三角形的腰时,
三角形的三边分别是
,,
符合三角形的三边关系,
周长为
;
当
为等腰三角形的腰时,
三边分别是
,,,符合三角形的三边关系,
周长为
.
12.
A
【解析】设购买
元的商品数量为
,购买
元的商品数量为
,
依题意得:,
整理,得
是正整数,
当
时,.
当
时,.
当
时
.
当
时,.
即有
种购买方案.
第二部分
13.
或
【解析】
在
中,,
恰好是直角三角形时,分两种情况:
①如果
是直角,那么
;
②如果
是直角,那么
.
14.
15.
【解析】依题意,得
,即
,
解得
.
16.
或
【解析】①当
为顶角时,等腰三角形两底角的度数为:,
特征值
.
②当
为底角时,顶角的度数为:,
特征值
.
综上所述,特征值
为
或
.
17.
【解析】
关于
的一元二次方程
的一个根是
,
,解得
.
第三部分
18.
19.
20.
(1)
,
,
同号.
又
,
,.
??????(2)
是方程
的一个根,
,即
,.
,
.
21.
(1)
,,
【解析】
点
,将点
向左平移
个单位再向上平移
个单位得到点
,
点
直线
上所有点的横坐标
与纵坐标
都是二元一次方程
的解.
直线
的解析式为:,
当
时,,
当
时,,
点
,点
.
??????(2)
如图
,连接
,.
,
.
??????(3)
设点
,如图
.
当点
在线段
上时,
,且
,
,
,
,
,
点
.
当点
在点
的左侧时,
,且
,
,
,
,
,
点
22.
(1)
【解析】
将①
②得
将③代入②得,,,
方程组解为
解坐标为
.
??????(2)
将④
⑤得,,,
将④
⑤得,,,
将
,
代入
得,
将⑥
⑦得,,,
将⑦
⑥得,,,
??????(3)
①
若要不存在解坐标,即无解,
需要
即
②若要有无数解坐标,即有无数解,
需要
即
第1页(共1
页)
同课章节目录
