人教版数学九年级上册 24.4 弧长和扇形面积 随堂练习(word版含答案)
文档属性
| 名称 | 人教版数学九年级上册 24.4 弧长和扇形面积 随堂练习(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 892.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-11 21:48:05 | ||
图片预览



文档简介
24.4
弧长和扇形面积
一、选择题(共12小题;共60分)
1.
如图,已知一块圆心角为
的扇形铁皮,用它作一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径是
,则这块扇形铁皮的半径是
A.
B.
C.
D.
2.
如图,将矩形
绕点
逆时针旋转
至矩形
,点
的旋转路径为
,若
,,则阴影部分的面积为
A.
B.
C.
D.
3.
在半径为
的圆中,弧长等于
的弧所对的圆心角是
A.
B.
C.
D.
4.
一个圆锥的底面半径
,高
,则这个圆锥的侧面积是
A.
B.
C.
D.
5.
如图所示,边长为
的正方形中阴影部分的面积为
A.
B.
C.
D.
6.
若一个圆锥的侧面展开图是半径为
,圆心角为
的扇形,则这个圆锥的底面半径长是
A.
B.
C.
D.
7.
制作一个圆锥模型,其侧面是用一个半径为
、圆心角为
的扇形铁皮围成的,则圆锥底面半径为
A.
B.
C.
D.
8.
已知圆锥的侧面展开图是一个半圆,则母线与高的夹角是
A.
B.
C.
D.
9.
如图,长方形木板的长为
,宽为
,某同学使之在桌面上做无滑动的翻滚(顺时针方向).木板上点
位置变化为
,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成
度角,则点
翻滚到
位置时走过的路径总长为
A.
B.
C.
D.
10.
圆锥的母线长为
,底面半径为
,则圆锥的侧面积是
.
A.
B.
C.
D.
11.
如图,正方形
的边
,
和
都是以
为半径的圆弧,则无阴影的两部分的面积之差是
A.
B.
C.
D.
12.
如图,水平地面上有一面积为
的扇形
,半径
,且
与地面垂直,在没有滑动的情况下,将扇形向右滚动至与三角块
接触为止,此时,扇表与地面的接触点为
,已知
,则
点移动的距离为
A.
B.
C.
D.
二、填空题(共5小题;共25分)
13.
如图,在半径为
的
中,圆心角
,则阴影部分面积为
?.
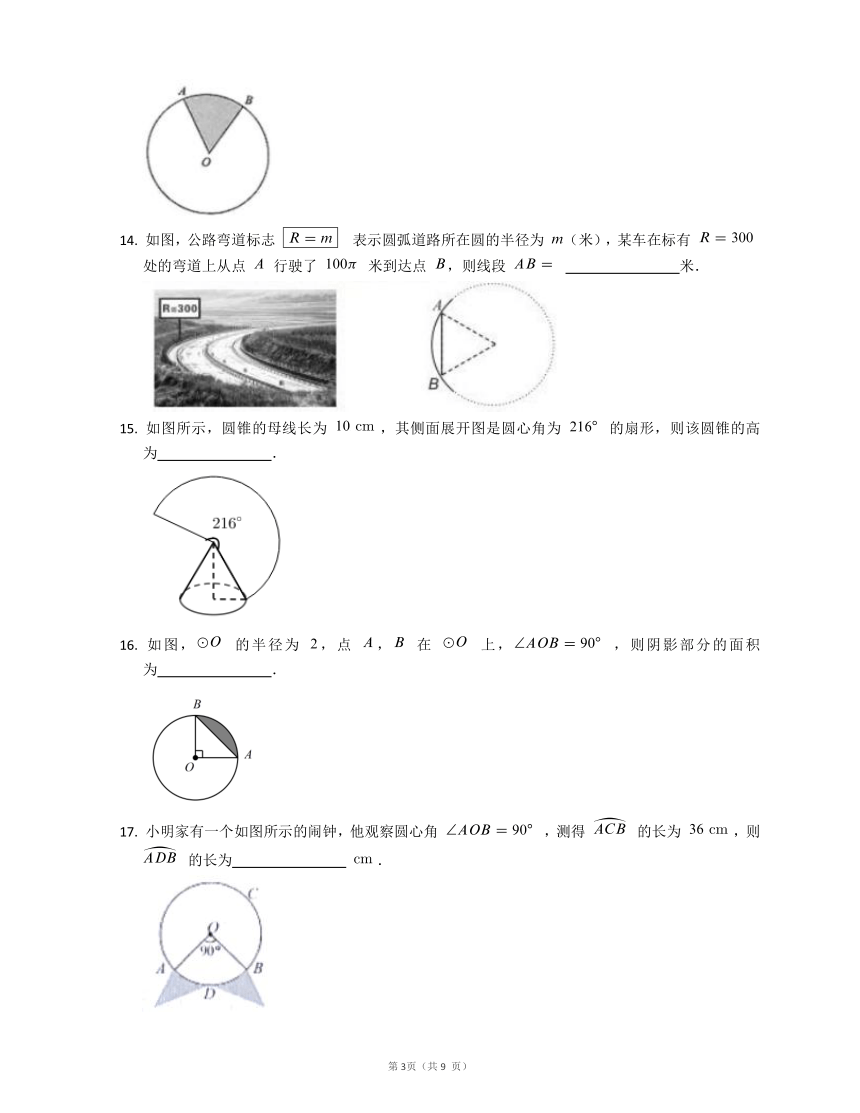
14.
如图,公路弯道标志
表示圆弧道路所在圆的半径为
(米),某车在标有
处的弯道上从点
行驶了
米到达点
,则线段
?米.
15.
如图所示,圆锥的母线长为
,其侧面展开图是圆心角为
的扇形,则该圆锥的高为
?.
16.
如图,
的半径为
,点
,
在
上,,则阴影部分的面积为
?.
17.
小明家有一个如图所示的闹钟,他观察圆心角
,测得
的长为
,则
的长为
?
.
三、解答题(共5小题;共65分)
18.
已知圆锥的底面半径为
,母线长为
.求它的侧面展开图的圆心角度数.
19.
如图,
是
的弦,
切
于点
,,垂足为
,
是
的半径,且
.
(1)求证:;
(2)若点
是优弧
上一点,且
,求扇形
的面积.(计算结果保留
)
20.
如图,
与
相切于
,,
分别交
于点
,,.
(1)求证:;
(2)已知,,,求阴影部分的面积.
21.
如图,正方形
的边长为
,以
点为圆心,
长为半径作
,求图中阴影部分的周长.
22.
如图,已知
的直径
,
是
的弦,过点
作
的切线交
的延长线于点
,连接
.
(1)求证:;
(2)已知
,点
在优弧
上,从点
开始逆时针运动到点
停止(点
与点
不重合),当
与
的面积相等时,求动点
所经过的弧长.
答案
第一部分
1.
A
【解析】
圆锥的底面直径为
,
圆锥的底面周长为
,
扇形的弧长为
,
设扇形的半径为
,则
,
解得:.
2.
D
【解析】如图,设
与
交于
,连接
,
,,
,
,
,
,
3.
C
【解析】设圆心角为
,,
,解得
.
4.
C
【解析】这个圆锥的母线长
,
这个圆锥的侧面积
.
5.
A
6.
C
【解析】设这个圆锥的底面半径为
,
根据题意得
,解得
,
这个圆锥的底面半径长为
.
7.
C
8.
B
【解析】设圆锥的母线长为
,底面半径为
,
因为圆锥的侧面展开图是半圆,
所以
,
所以
,
所以母线与高的夹角的正弦值
,
所以母线与高的夹角是
.
9.
B
10.
C
11.
A
12.
C
第二部分
13.
【解析】阴影部分面积为
.
14.
15.
【解析】扇形的弧长为:,
则圆锥的底面半径为:,
由勾股定理得,圆锥的高为:.
16.
17.
【解析】设半径
的长为
.
,
,,
,
.
第三部分
18.
设该圆心角的度数为
,
.
,
解得
.
圆心角的度数为
.
19.
(1)
连接
,
切
于点
,
,
,
,
.
,
,
,
平分
.
??????(2)
点
在
上,且
,
,
.
20.
(1)
连
,
则
.
又因为
,
所以
,
在
和
中,
所以
,
所以
.
??????(2)
由()可得
,
在
中,,
所以
,
所以
.
,
所以
.
21.
阴影部分的周长为:
.
22.
(1)
连接
.
因为
是
的切线,
所以
.
所以
.
因为
是
的直径,
所以
.
所以
.
因为
,
所以
.
所以
.
??????(2)
因为
,
所以
.
因为
,
所以
.
当
时,
与
的面积相等,
所以点
所经过的
.
当
时,即
时,
与
的面积相等,
所以点
所经过的
.
当
时,即
时,
与
的面积相等,
所以点
所经过的
.
所以当
与
的面积相等时,动点
所经过的弧长为
或
或
.
第1页(共1
页)
弧长和扇形面积
一、选择题(共12小题;共60分)
1.
如图,已知一块圆心角为
的扇形铁皮,用它作一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径是
,则这块扇形铁皮的半径是
A.
B.
C.
D.
2.
如图,将矩形
绕点
逆时针旋转
至矩形
,点
的旋转路径为
,若
,,则阴影部分的面积为
A.
B.
C.
D.
3.
在半径为
的圆中,弧长等于
的弧所对的圆心角是
A.
B.
C.
D.
4.
一个圆锥的底面半径
,高
,则这个圆锥的侧面积是
A.
B.
C.
D.
5.
如图所示,边长为
的正方形中阴影部分的面积为
A.
B.
C.
D.
6.
若一个圆锥的侧面展开图是半径为
,圆心角为
的扇形,则这个圆锥的底面半径长是
A.
B.
C.
D.
7.
制作一个圆锥模型,其侧面是用一个半径为
、圆心角为
的扇形铁皮围成的,则圆锥底面半径为
A.
B.
C.
D.
8.
已知圆锥的侧面展开图是一个半圆,则母线与高的夹角是
A.
B.
C.
D.
9.
如图,长方形木板的长为
,宽为
,某同学使之在桌面上做无滑动的翻滚(顺时针方向).木板上点
位置变化为
,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成
度角,则点
翻滚到
位置时走过的路径总长为
A.
B.
C.
D.
10.
圆锥的母线长为
,底面半径为
,则圆锥的侧面积是
.
A.
B.
C.
D.
11.
如图,正方形
的边
,
和
都是以
为半径的圆弧,则无阴影的两部分的面积之差是
A.
B.
C.
D.
12.
如图,水平地面上有一面积为
的扇形
,半径
,且
与地面垂直,在没有滑动的情况下,将扇形向右滚动至与三角块
接触为止,此时,扇表与地面的接触点为
,已知
,则
点移动的距离为
A.
B.
C.
D.
二、填空题(共5小题;共25分)
13.
如图,在半径为
的
中,圆心角
,则阴影部分面积为
?.
14.
如图,公路弯道标志
表示圆弧道路所在圆的半径为
(米),某车在标有
处的弯道上从点
行驶了
米到达点
,则线段
?米.
15.
如图所示,圆锥的母线长为
,其侧面展开图是圆心角为
的扇形,则该圆锥的高为
?.
16.
如图,
的半径为
,点
,
在
上,,则阴影部分的面积为
?.
17.
小明家有一个如图所示的闹钟,他观察圆心角
,测得
的长为
,则
的长为
?
.
三、解答题(共5小题;共65分)
18.
已知圆锥的底面半径为
,母线长为
.求它的侧面展开图的圆心角度数.
19.
如图,
是
的弦,
切
于点
,,垂足为
,
是
的半径,且
.
(1)求证:;
(2)若点
是优弧
上一点,且
,求扇形
的面积.(计算结果保留
)
20.
如图,
与
相切于
,,
分别交
于点
,,.
(1)求证:;
(2)已知,,,求阴影部分的面积.
21.
如图,正方形
的边长为
,以
点为圆心,
长为半径作
,求图中阴影部分的周长.
22.
如图,已知
的直径
,
是
的弦,过点
作
的切线交
的延长线于点
,连接
.
(1)求证:;
(2)已知
,点
在优弧
上,从点
开始逆时针运动到点
停止(点
与点
不重合),当
与
的面积相等时,求动点
所经过的弧长.
答案
第一部分
1.
A
【解析】
圆锥的底面直径为
,
圆锥的底面周长为
,
扇形的弧长为
,
设扇形的半径为
,则
,
解得:.
2.
D
【解析】如图,设
与
交于
,连接
,
,,
,
,
,
,
3.
C
【解析】设圆心角为
,,
,解得
.
4.
C
【解析】这个圆锥的母线长
,
这个圆锥的侧面积
.
5.
A
6.
C
【解析】设这个圆锥的底面半径为
,
根据题意得
,解得
,
这个圆锥的底面半径长为
.
7.
C
8.
B
【解析】设圆锥的母线长为
,底面半径为
,
因为圆锥的侧面展开图是半圆,
所以
,
所以
,
所以母线与高的夹角的正弦值
,
所以母线与高的夹角是
.
9.
B
10.
C
11.
A
12.
C
第二部分
13.
【解析】阴影部分面积为
.
14.
15.
【解析】扇形的弧长为:,
则圆锥的底面半径为:,
由勾股定理得,圆锥的高为:.
16.
17.
【解析】设半径
的长为
.
,
,,
,
.
第三部分
18.
设该圆心角的度数为
,
.
,
解得
.
圆心角的度数为
.
19.
(1)
连接
,
切
于点
,
,
,
,
.
,
,
,
平分
.
??????(2)
点
在
上,且
,
,
.
20.
(1)
连
,
则
.
又因为
,
所以
,
在
和
中,
所以
,
所以
.
??????(2)
由()可得
,
在
中,,
所以
,
所以
.
,
所以
.
21.
阴影部分的周长为:
.
22.
(1)
连接
.
因为
是
的切线,
所以
.
所以
.
因为
是
的直径,
所以
.
所以
.
因为
,
所以
.
所以
.
??????(2)
因为
,
所以
.
因为
,
所以
.
当
时,
与
的面积相等,
所以点
所经过的
.
当
时,即
时,
与
的面积相等,
所以点
所经过的
.
当
时,即
时,
与
的面积相等,
所以点
所经过的
.
所以当
与
的面积相等时,动点
所经过的弧长为
或
或
.
第1页(共1
页)
同课章节目录
