人教版数学七年级下册5.1.1 相交线 导学案(无答案)
文档属性
| 名称 | 人教版数学七年级下册5.1.1 相交线 导学案(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 665.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-11 00:00:00 | ||
图片预览

文档简介
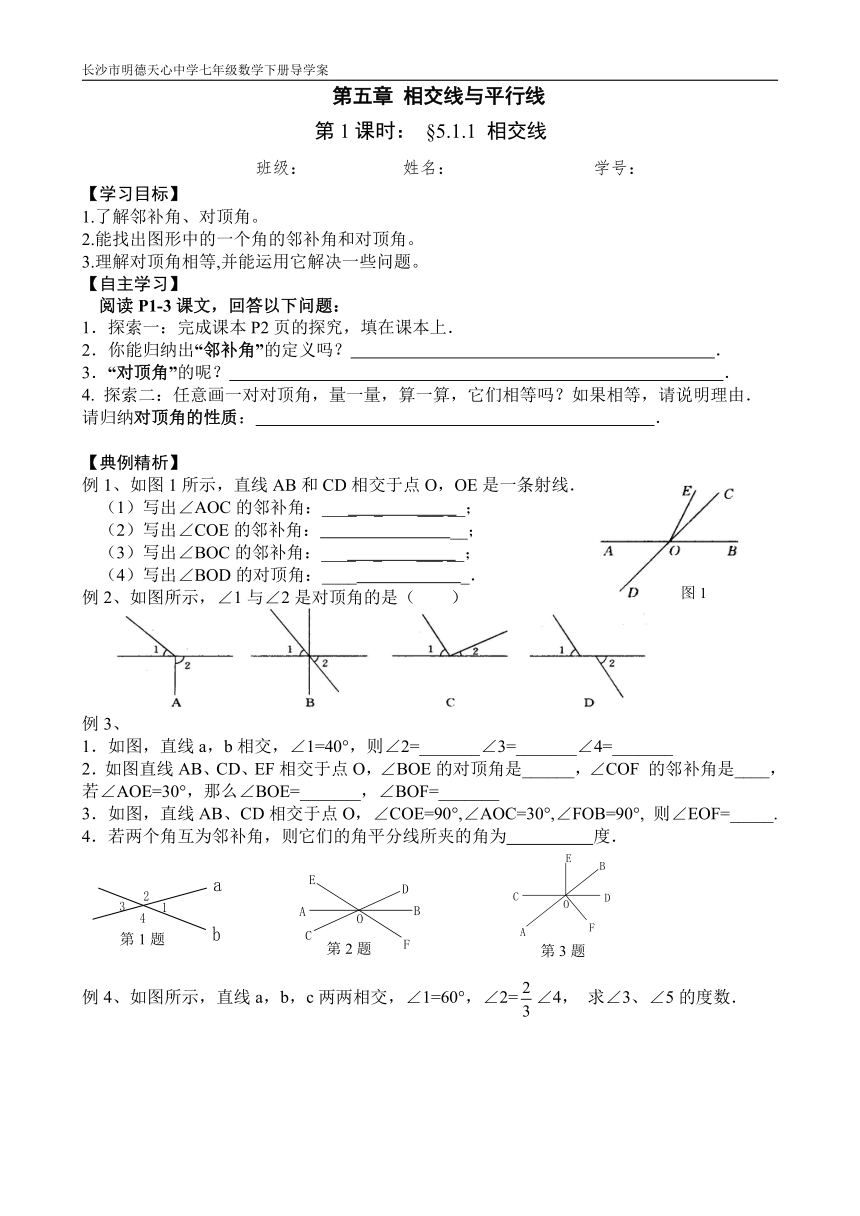
长沙市明德天心中学七年级数学下册导学案
第五章
相交线与平行线
第1课时:
§5.1.1
相交线
班级:
姓名:
学号:
【学习目标】
1.了解邻补角、对顶角。
2.能找出图形中的一个角的邻补角和对顶角。
3.理解对顶角相等,并能运用它解决一些问题。
【自主学习】
阅读P1-3课文,回答以下问题:
1.探索一:完成课本P2页的探究,填在课本上.
2.你能归纳出“邻补角”的定义吗?
.
3.“对顶角”的呢?
.
4.
探索二:任意画一对对顶角,量一量,算一算,它们相等吗?如果相等,请说明理由.
请归纳对顶角的性质:
.
【典例精析】
例1、如图1所示,直线AB和CD相交于点O,OE是一条射线.
(1)写出∠AOC的邻补角:____
_
___
__;
(2)写出∠COE的邻补角:
__;
(3)写出∠BOC的邻补角:____
_
___
__;
(4)写出∠BOD的对顶角:____
_.
例2、如图所示,∠1与∠2是对顶角的是(
)
例3、
1.如图,直线a,b相交,∠1=40°,则∠2=_______∠3=_______∠4=_______
2.如图直线AB、CD、EF相交于点O,∠BOE的对顶角是______,∠COF
的邻补角是____,若∠AOE=30°,那么∠BOE=_______,∠BOF=_______
3.如图,直线AB、CD相交于点O,∠COE=90°,∠AOC=30°,∠FOB=90°,
则∠EOF=_____.
4.若两个角互为邻补角,则它们的角平分线所夹的角为
度.
例4、如图所示,直线a,b,c两两相交,∠1=60°,∠2=∠4,求∠3、∠5的度数.
【分层作业】
A组·复习巩固
1.如图1所示,直线AB,CD相交于点O,因为∠1+∠3=180°,∠2+∠3=180°,所以∠1=∠2,其推理依据为
( )
A.对顶角相等
B.同角的余角相等
C.邻补角的定义
D.同角的补角相等
图1
图2
图3
图4
2.如图2所示,已知点O是直线AB上一点,∠1=40°,OD平分∠BOC,则∠2的度数
( )
A.20°
B.25°
C.30°
D.70°
3.如图3所示,直线AB,CD相交于点O,OE,OF为射线,则对顶角有( )
A.1对
B.2对
C.3对
D.4对
4.如图4所示,直线AB,CD相交于点O,OE平分∠AOD,若∠BOC=80°,则∠AOE的度数是
( )
A.40°
B.50°
C.80°
D.100°
5.如图5,AB,CD相交于点O,∠AOE=90°,则∠AOC和∠BOD是________,∠AOC与∠AOD是________,∠AOC与∠DOE的关系是________________.
图
5
图
6
图
7
图
8
6.如图6,直线AB,CD相交于点O,OE平分∠AOD,若∠BOD=100°,则∠AOE=__
__.
7.如图7,直线AB,CD相交于点O,OE平分∠BOD,且∠AOC=∠COB-30°,则∠AOE=___.
B组·综合运用
8.如图8,已知直线AD与BE相交于点O,∠DOE与∠COE互余,∠COE=62°,求∠AOB的度数.
9.如图9,直线AB,CD相交于点O,∠1=∠2,∠COE=70°,那么∠COB等于多少度?
C组·拓广探索
10.(1)两条直线相交于一点,有________对对顶角;
(2)三条直线相交于一点,有________对对顶角;
(3)四条直线相交于一点,有________对对顶角;
(4)n条直线相交于一点,有________对对顶角.
第五章
相交线与平行线
第1课时:
§5.1.1
相交线
班级:
姓名:
学号:
【学习目标】
1.了解邻补角、对顶角。
2.能找出图形中的一个角的邻补角和对顶角。
3.理解对顶角相等,并能运用它解决一些问题。
【自主学习】
阅读P1-3课文,回答以下问题:
1.探索一:完成课本P2页的探究,填在课本上.
2.你能归纳出“邻补角”的定义吗?
.
3.“对顶角”的呢?
.
4.
探索二:任意画一对对顶角,量一量,算一算,它们相等吗?如果相等,请说明理由.
请归纳对顶角的性质:
.
【典例精析】
例1、如图1所示,直线AB和CD相交于点O,OE是一条射线.
(1)写出∠AOC的邻补角:____
_
___
__;
(2)写出∠COE的邻补角:
__;
(3)写出∠BOC的邻补角:____
_
___
__;
(4)写出∠BOD的对顶角:____
_.
例2、如图所示,∠1与∠2是对顶角的是(
)
例3、
1.如图,直线a,b相交,∠1=40°,则∠2=_______∠3=_______∠4=_______
2.如图直线AB、CD、EF相交于点O,∠BOE的对顶角是______,∠COF
的邻补角是____,若∠AOE=30°,那么∠BOE=_______,∠BOF=_______
3.如图,直线AB、CD相交于点O,∠COE=90°,∠AOC=30°,∠FOB=90°,
则∠EOF=_____.
4.若两个角互为邻补角,则它们的角平分线所夹的角为
度.
例4、如图所示,直线a,b,c两两相交,∠1=60°,∠2=∠4,求∠3、∠5的度数.
【分层作业】
A组·复习巩固
1.如图1所示,直线AB,CD相交于点O,因为∠1+∠3=180°,∠2+∠3=180°,所以∠1=∠2,其推理依据为
( )
A.对顶角相等
B.同角的余角相等
C.邻补角的定义
D.同角的补角相等
图1
图2
图3
图4
2.如图2所示,已知点O是直线AB上一点,∠1=40°,OD平分∠BOC,则∠2的度数
( )
A.20°
B.25°
C.30°
D.70°
3.如图3所示,直线AB,CD相交于点O,OE,OF为射线,则对顶角有( )
A.1对
B.2对
C.3对
D.4对
4.如图4所示,直线AB,CD相交于点O,OE平分∠AOD,若∠BOC=80°,则∠AOE的度数是
( )
A.40°
B.50°
C.80°
D.100°
5.如图5,AB,CD相交于点O,∠AOE=90°,则∠AOC和∠BOD是________,∠AOC与∠AOD是________,∠AOC与∠DOE的关系是________________.
图
5
图
6
图
7
图
8
6.如图6,直线AB,CD相交于点O,OE平分∠AOD,若∠BOD=100°,则∠AOE=__
__.
7.如图7,直线AB,CD相交于点O,OE平分∠BOD,且∠AOC=∠COB-30°,则∠AOE=___.
B组·综合运用
8.如图8,已知直线AD与BE相交于点O,∠DOE与∠COE互余,∠COE=62°,求∠AOB的度数.
9.如图9,直线AB,CD相交于点O,∠1=∠2,∠COE=70°,那么∠COB等于多少度?
C组·拓广探索
10.(1)两条直线相交于一点,有________对对顶角;
(2)三条直线相交于一点,有________对对顶角;
(3)四条直线相交于一点,有________对对顶角;
(4)n条直线相交于一点,有________对对顶角.
