苏科版七年级数学下册7.2平行线的性质自主学习同步提升训练(Word版 附答案)
文档属性
| 名称 | 苏科版七年级数学下册7.2平行线的性质自主学习同步提升训练(Word版 附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 664.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-12 00:00:00 | ||
图片预览



文档简介
2021年苏科新版七年级数学下册7.2平行线的性质自主学习同步提升训练(附答案)
1.如图,若直线a∥b,那么∠x=( )
A.64°
B.68°
C.69°
D.66°
2.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,则两次拐弯的角度可以是( )
A.第一次向右拐40°第二次向左拐140°
B.第一次向左拐40°第二次向右拐40°C.第一次向左拐40°第二次向右拐140°
D.第一次向右拐40°第二次向右拐40°
3.小张同学观察如图1所示的北斗七星图,小张同学把北斗七星:摇光、开阳、玉衡、天权、天玑、天璇、天枢按图2分别标为点A,B,C,D,E,F,G,然后将点A,B,C,D,E,F,G顺次首尾连接,发现AG恰好经过点C,且∠B﹣∠DCG=115°,∠B﹣∠D=10°,若AG∥EF,则∠E=m°,这里的m=
.
4.如图,一束光线从点C出发,经过平面镜AB反射后,沿与AF平行的线段DE射出(此时∠1=∠2),若测得∠DCF=100°,则∠A=
.
5.如图,已知直线AB∥CD,MN分别交AB,CD于点E,F,∠BEF与∠DFE的两条平分线相交于点P1,∠BEP1与∠DFP1的两条平分线相交于点P2,则∠P2的度数为
.
6.如图1,已知∠ACB=80°,点A在直线EF上,点B在直线GH上,且∠CAE+∠CBG=80°.
(1)试判断直线EF与GH的位置关系,并说明理由;
(2)如图2,若点B在直线GH上运动,作∠CAP=2∠CAE,作∠CBP=2∠CBG,试判断∠APB的大小是否会随着点B的运动而发生变化?若不变,求出∠APB的大小;若变化,请说明理由.
7.如图,直线CB∥OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值.
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.
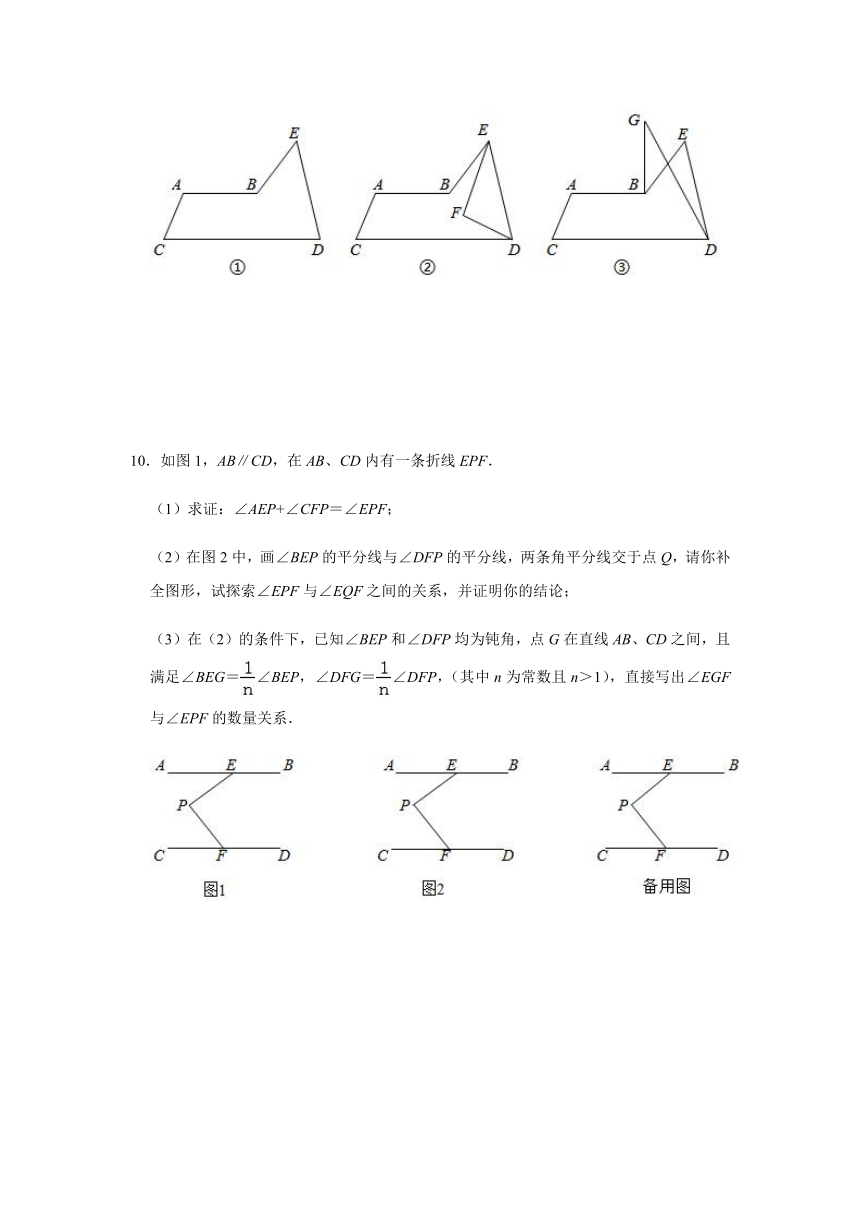
8.阅读下?材料,完成(1)~(3)题.
数学课上,?师出示了这样?道题:
如图1,已知AB∥CD,点E,F分别在AB,CD上,EP⊥FP,∠1=60°.求∠2的度数.
同学们经过思考后,?明、?伟、?华三位同学?不同的?法添加辅助线,交流了??的想法:
?明:“如图2,通过作平?线,发现∠1=∠3,∠2=∠4,由已知EP⊥FP,可以求出∠2的度数.”
?伟:“如图3这样作平?线,经过推理,得∠2=∠3=∠4,也能求出∠2的度数.”
?华:“如图4,也能求出∠2的度数.”
(1)请你根据?明同学所画的图形(图2),描述?明同学辅助线的做法,辅助线:
;
(2)请你根据以上同学所画的图形,直接写出∠2的度数为
°;
?师:“这三位同学解法的共同点,都是过?点作平?线来解决问题,这个?法可以推?.”
请?家参考这三位同学的?法,使?与他们类似的?法,解决下?的问题:
(3)如图5,AB∥CD,点E,F分别在AB,CD上,FP平分∠EFD,∠PEF=∠PDF,若∠EPD=α,请探究∠CFE与∠PEF的数量关系(?含α的式?表示),并验证你的结论.
9.如图,AB∥CD,∠ABE=120°.
(1)如图①,写出∠BED与∠D的数量关系,并证明你的结论;
(2)如图②,∠DEF=2∠BEF,∠CDF=∠CDE,EF与DF交于点F,求∠EFD的度数;
(3)如图③,过B作BG⊥AB于G点,∠CDE=4∠GDE,求的值.
10.如图1,AB∥CD,在AB、CD内有一条折线EPF.
(1)求证:∠AEP+∠CFP=∠EPF;
(2)在图2中,画∠BEP的平分线与∠DFP的平分线,两条角平分线交于点Q,请你补全图形,试探索∠EPF与∠EQF之间的关系,并证明你的结论;
(3)在(2)的条件下,已知∠BEP和∠DFP均为钝角,点G在直线AB、CD之间,且满足∠BEG=∠BEP,∠DFG=∠DFP,(其中n为常数且n>1),直接写出∠EGF与∠EPF的数量关系.
11.如图,直线PQ∥MN,点C是PQ、MN之间(不在直线PQ,MN上)的一个动点.
(1)如图1,若∠1与∠2都是锐角,请写出∠C与∠1,∠2之间的数量关系并说明理由.
(2)把Rt△ABC如图2摆放,直角顶点C在两条平行线之间,CB与PQ交于点D,CA与MN交于点E,BA与PQ交于点F,点G在线段CE上,连接DG,有∠BDF=∠GDF,求的值.
(3)如图3,若点D是MN下方一点,BC平分∠PBD,AM平分∠CAD,已知∠PBC=25°,求∠ACB+∠ADB的度数.
12.阅读下列推理过程,在括号中填写理由.
如图,AB∥CD∥GH,EG平分∠BEF,FG平分∠EFD,求证:∠EGF=90°.
证明:∵AB∥GH(已知),
∴∠1=∠3(
),
又∵CD∥GH(已知),
∴
(两直线平行,内错角相等).
∵AB∥CD(已知),
∴∠BEF+
=180°(两直线平行,同旁内角互补).
∵EG平分∠BEF(已知),
∴∠1=
(
),
又∵FG平分∠EFD(已知),
∴∠2=∠EFD(
),
∴∠1+∠2=(
+∠EFD),
∴∠1+∠2=90°,
∴∠3+∠4=90°(
),即∠EGF=90°.
13.(1)如图甲,AB∥CD,∠BEC与∠1+∠3的关系是什么?并写出推理过程;
(2)如图乙,AB∥CD,直接写出∠2+∠4与∠1+∠3+∠5的数量关系
;
(3)如图丙,AB∥CD,直接写出∠2+∠4+∠6与∠1+∠3+∠5+∠7的数量关系
.
14.已知:直线AB∥CD,点E,F分别在直线AB,CD上,点M为两平行线内部一点.
(1)如图1,∠AEM,∠M,∠CFM的数量关系为
;(直接写出答案)
(2)如图2,∠MEB和∠MFD的角平分线交于点N,若∠EMF等于130°,求∠ENF的度数;
(3)如图3,点G为直线CD上一点,延长GM交直线AB于点Q,点P为MG上一点,射线PF、EH相交于点H,满足∠PFG=∠MFG,∠BEH=∠BEM,设∠EMF=α,求∠H的度数(用含α的代数式表示).
15.如图,AB∥CD,点C在点D的右侧,∠ABC,∠ADC的平分线交于点E(不与B,D点重合),∠ADC=70°.设∠BED=n°.
(1)若点B在点A的左侧,求∠ABC的度数;(用含n的代数式表示)
(2)将(1)中的线段BC沿DC方向平移,当点B移动到点A右侧时,请画出图形并判断∠ABC的度数是否改变.若改变,请求出∠ABC的度数(用含n的代数式表示);若不变,请说明理由.
16.如图所示,直线AB∥CD,直线EF分别交AB、CD于E、F两点,∠BEF、∠DFE的平分线相交于点K.
(1)求∠EKF的度数;
(2)如图(2)所示,作∠BEK、∠DFK的平分线相交于点K1,问∠K1与∠K的度数是否存在某种特定的等量关系?写出结论并证明.
(3)在图(2)中作∠BEK1、∠DFK1的平分线相交于点K2,作∠BEK2、∠DFK2的平分线相交于点K3,依此类推,……,请直接写出∠K4的度数.
17.如图所示,四边形ABCD中,AE平分∠DAB,AE∥CF,∠B=∠D=90°.求证:CF平分∠BCD.
18.直线AB∥CD,E为直线AB、CD之间的一点,完成以下问题:
(1)如图1,若∠B=15°,∠BED=90°,则∠D=
;
(2)如图2,若∠B=α,∠D=β,求出∠BED的度数(用a、β表示);
(3)如图3,若∠B=α,∠C=β,则a、β与∠BEC之间有什么等量关系?请猜想证明.
19.如图,AB∥CD,定点E,F分别在直线AB,CD上,在平行线AB,CD之间有一动点P,且满足0°<∠EPF<180°,QE,QF分别平分∠PEB和∠PFD.
在探究∠EPF与∠EQF之间的数量关系时,我们需要对点P的位置进行分类讨论:
(1)如图1,当P点在EF的右侧时,若∠EPF=110°,则∠EQF=
;
猜想∠EPF与∠EQF的数量关系,请直接写出结果;
(2)如图2,当P点在EF的左侧时,探究∠EPF与∠EQF的数量关系,请说明理由;
(3)若∠BEQ与∠DFQ的角平分线交于点Q1,∠BEQ1与∠DFQ1的角平分线交于点Q2,∠BEQ2与∠DFQ2的角平分线交于点Q3;…以此类推,则∠EPF与∠EQnF满足怎样的数量关系?(直接写出结果)
20.直线AB、CD被直线EF所截,AB∥CD,点P是平面内一动点.
(1)若点P在直线CD上,如图①,∠α=50°,则∠2=
°.
(2)若点P在直线AB、CD之间,如图②,试猜想∠α、∠1、∠2之间的等量关系并给出证明;
(3)若点P在直线CD的下方,如图③,(2)中∠α、∠1、∠2之间的关系还成立吗?请作出判断并说明理由.
21.如图1,AB∥CD,在AB、CD内有一条折线EPF.
(1)求证:∠AEP+∠CFP=∠EPF;
(2)如图2,已知∠BEP的平分线与∠DFP的平分线相交于点Q,试探索∠EPF与∠EQF之间的关系.
(3)已知∠BEQ=∠BEP,∠DFQ=∠DFP,有∠P与∠Q的关系为
.(直接写结论)
22.综合探究:
已知,AB∥CD,点M、N分别是AB、CD上两点,点G在AB、CD之间,连接MG、NG.
(1)如图1,若GM⊥GN,求∠AMG+∠CNG的度数;
(2)如图2,若点P是CD下方一点,MG平分∠BMP,ND平分∠GNP,已知∠BMG=40°,求∠MGN+∠MPN的度数.
23.如图,已知AB∥CD,点P是AB、CD之间的任意一点且在AC右侧.
(1)∠APC与∠BAP、∠DCP的数量关系是
;
(2)∠BAP的平分线所在直线与∠DCP的邻补角平分线相交于点Q,∠BAP=α.
①根据题意,在图中补全图形,判断∠APC与∠AQC的数量关系并说明理由;
②若AP∥CQ,求∠DCP的度数(用含α的式子表示).
24.已知一个角的两边与另一个角的两边分别平行,结合图,试探索这两个角之间的关系,并说明你的结论.
(1)如图1,AB∥EF,BC∥DE,∠1与∠2有何关系?说明理由;
(2)如图2,AB∥EF,BC∥DE,∠1与∠2有何关系?说明理由;
(3)由(1)(2)你能得出的结论是:如果
,那么
;
(4)若两个角的两边分别平行,且一个角比另一个角的2倍少60°,则这两个角度数的分别是
.
25.已知AB∥CD,点E在AB与CD之间.
(1)图1中,试说明:∠BED=∠ABE+∠CDE;
(2)图2中,∠ABE的平分线与∠CDE的平分线相交于点F,请利用(1)的结论说明:∠BED=2∠BFD.
(3)图3中,∠ABE的平分线与∠CDE的平分线相交于点F,请直接写出∠BED与∠BFD之间的数量关系.
26.如图,∠ABC+∠ECB=180°,∠P=∠Q.求证:∠1=∠2.
在下列解答中,填空:
证明:∵∠ABC+∠ECB=180°(已知),
∴AB∥DE(
).
∴∠ABC=∠BCD(
).
∵∠P=∠Q(已知),
∴PB∥(
)(
).
∴∠PBC=(
)(两直线平行,内错角相等).
∵∠1=∠ABC﹣(
),∠2=∠BCD﹣(
),
∴∠1=∠2(等量代换).
27.已知点A在射线CE上,∠BDA=∠C.
(1)如图1,若AC∥BD,求证:AD∥BC;
(2)如图2,若∠BAC=∠BAD,BD⊥BC,请证明∠DAE+2∠C=90°;
(3)如图3,在(2)的条件下,过点D作DF∥BC交射线CE于点F,当∠DFE=8∠DAE时,求∠BAD的度数.(直接写出结果)
28.如图,已知AD∥BC,AE平分∠BAD交BC延长线于点E,CD与AE相交于点F,∠CFE=∠E,求证:AB∥DC.
29.(1)阅读并回答:
科学实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的角相等.如图1,一束平行光线AB与DE射向一个水平镜面后被反射,此时∠1=∠2,∠3=∠4.
①由条件可知:∠1与∠3的大小关系是
,理由是
;∠2与∠4的大小关系是
;
②反射光线BC与EF的位置关系是
,理由是
.
(2)解决问题:
如图2.一束光线m射到平面镜a上,被a反射到平面镜b上,又被b镜反射,若b反射出的光线n平行于m,且∠1=40°,求∠2和∠3的度数.
30.已知:如图,点B,C,E在一条直线上,点A、E、F在一条直线上,AB∥CD,∠1=∠2,∠3=∠4.求证:AD∥BE.
31.某学习小组发现一个结论:已知直线a∥b,若直线c∥a,则c∥b.他们发现这个结论运用很广,请你利用这个结论解决以下问题:
已知直线AB∥CD,点E在AB、CD之间,点P、Q分别在直线AB、CD上,连接PE、EQ.
(1)如图1,过点E作EH∥AB,运用上述结论,探究∠PEQ、∠APE、∠CQE之间的数量关系,并说明理由;
(2)如图2,类比(1)中的方法,运用上述结论,探究∠PEQ、∠APE、∠CQE之间的数量关系,并说明理由;
(3)如图3,PF平分∠BPE,QF平分∠EQD,当∠PEQ=140°时,直接写出∠PFQ的度数.
32.实验证明:平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.如图有两块互相垂直的平面镜MN、NP.一束光线AB射在其中一块MN上,经另外一块NP反射.两束光线会平行吗?若不平行,请说明理由,若平行,请给予证明.
33.请阅读小明同学在学习平行线这章知识点时的一段笔记,然后解决问题.
小明:老师说在解决有关平行线的问题时,如果无法直接得到角的关系,就需要借助辅助线来帮助解答,今天老师介绍了一个“美味”的模型﹣﹣﹣“猪蹄模型”.即
已知:如图1,AB∥CD,E为AB、CD之间一点,连接AE,CE得到∠AEC.
求证:∠AEC=∠A+∠C.
小明笔记上写出的证明过程如下:
证明:过点E作EF∥AB,
∴∠1=∠A.
∵AB∥CD,EF∥AB,
∴EF∥CD.
∴∠2=∠C.
∵∠AEC=∠1+∠2,
∴∠AEC=∠A+∠C.
请你利用“猪蹄模型”得到的结论或解题方法,完成下面的两个问题.
(1)如图2,若AB∥CD,∠E=60°,则∠B+∠C+∠F=
.
(2)如图3,AB∥CD,BE平分∠ABG,CF平分∠DCG,∠G=∠H+27°,则∠H=
.
34.实验证明,平面镜反射光线的规律是:照射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.
(1)如图,一束光线MA照射到平面镜CE上,被CE反射到平面镜CF上,又被CF反射.已知被CF反射出的光线BN与光线MA平行.若∠1=35°,则∠2=
,∠3=
;若∠1=50°,∠3=
.
(2)由(1)猜想:当两平面镜CE,CF的夹角∠3为多少度时,可以使任何射到平面镜CE上的光线MA,经过平面镜CE,CF的两次反射后,入射光线MA与反射光线BN平行,请你写出推理过程.
35.感知与填空:如图①,直线AB∥CD.求证:∠B+∠D=∠BED.
阅读下面的解答过程,井填上适当的理由.
解:过点E作直线EF∥CD
∴∠2=∠D(
)
∵AB∥CD(已知),EF∥CD,
∴AB∥EF(
)
∴∠B=∠1(
)
∵∠1+∠2=∠BED,
∴∠B+∠D=∠BED(
)
应用与拓展:如图②,直线AB∥CD.若∠B=22°,∠G=35°,∠D=25°,则∠E+∠F=
度.
方法与实践:如图③,直线AB∥CD.若∠E=∠B=60°,∠F=80°,则∠D=
度.
36.如图(1),AB∥CD,试求∠BPD与∠B、∠D的数量关系,说明理由.
(1)填空:
解:过点P作EF∥AB,
∴∠B+∠BPE=180°
∵AB∥CD,EF∥AB
∴
(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∠EPD+
=180°
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
(2)依照上面的解题方法,观察图(2),已知AB∥CD,猜想图中的∠BPD与∠B、∠D的数量关系,并说明理由.
(3)观察图(3)和(4),已知AB∥CD,直接写出图中的∠BPD与∠B、∠D的数量关系,不用说明理由.
37.已知:如图,∠1=∠2,∠B=∠C,求证:∠A=∠D.
38.已知如图,DE⊥AC,∠AGF=∠ABC,∠1+∠2=180°,试判断BF与AC的位置关系,并说明理由.
39.已知:如图,∠1=∠2,∠3=∠4,∠5=∠6.求证:ED∥FB
参考答案
1.解:令与130°互补的角为∠1,如图所示.
∵∠1+130°=180°,
∴∠1=50°.
∵a∥b,
∴x+48°+20°=∠1+30°+52°,
∴x=64°.
故选:A.
2.解:A、如图1:∵∠1=40°,∠2=140°,
∴AB与CD不平行;
故本选项错误;
B、如图2:∵∠1=40°,∠2=40°,
∴∠1=∠2,
∴AB与CD平行;
故本选项正确;
C、如图3:∵∠1=40°,∠2=140°,
∴∠1≠∠2,
∴AB不平行CD;
故本选项错误;
D、如图4:∠1=40°,∠2=40°,
∴∠3=140°,
∴∠1≠∠3,
∴AB与CD不平行;
故本选项错误.
故选:B.
3.解:延长ED交AG于点H,
∵AG∥EF,
∴∠E=∠CHD,
∴∠CHD=∠CDE﹣∠DCG,
∵∠B﹣∠DCG=115°,∠B﹣∠CDE=10°,
∴∠CDE=∠B﹣10°,∠DCG=∠B﹣115°,
∴∠E=∠CHD=∠B﹣10°﹣(∠B﹣115°)=105°,
故答案为:105.
4.解:∵DE∥AF,
∴∠2=∠A,
∵∠1=∠2,
∴∠1=∠2=∠A,
∵∠DCF=∠A+∠1=2∠A=100°,
∴∠A=50°,
故答案为:50°.
5.解:过P1作P1G∥AB,可得P1G∥CD,如图,
∴∠BEP1=∠EP1G,∠GP1F=∠P1FD,
∵EP1、FP1分别为∠BEF与∠EFD的平分线,
∴∠BEP1=∠FEP1,∠EFP1=∠DFP1,
∵AB∥CD,
∴∠BEP1+∠FEP1+∠EFP1+∠DFP1=180°,即2(∠BEP1+∠DFP1)=180°,
∴∠BEP1+∠DFP1=90°,
∵∠BEP1、∠DFP1的平分线相交于点K1,
∴∠BEP2=∠P1EP2,∠P1FP2=∠DFP2,
∵∠BEP1+∠FEP1+∠EFP1+∠DFP1=180°,即2(∠BEP1+∠P1FD)=180°,
∴∠BEP1+∠P1FD=90°,即∠P1EP2+∠P1FP2=45°,
∴∠K1=180°﹣(∠P1EF+∠EFP1)﹣(∠P1EP2+∠P1FP2)=45°,
故答案为:45°.
6.解;(1)直线EF与GH的位置关系是平行,理由如下:
如图1,过点C作CD∥EF,
∴∠CAE=∠ACD,
∵∠ACB=∠ACD+∠BCD=80°,∠CAE+∠CBG=80°.
∴∠BCD=∠CBG,
∴CD∥GH,
∴EF∥GH;
(2)∠APB的大小不会随着点B的运动而发生变化,理由如下:
如图2,∵∠CAP=2∠CAE,∠CBP=2∠CBG,
∴∠CAP+∠CBP=2∠CAE+2∠CBG=2(∠CAE+∠CBG)=2×80°=160°,
∴∠APB=360°﹣∠ACB﹣(∠CAP+∠CBP)=360°﹣80°﹣160°=120°.
所以∠APB的大小为120°.
7.解:(1)∵CB∥OA,
∴∠AOC=180°﹣∠C=180°﹣100°=80°,
∵OE平分∠COF,
∴∠COE=∠EOF,
∵∠FOB=∠AOB,
∴∠EOB=∠EOF+∠FOB=∠AOC=×80°=40°;
(2)∵CB∥OA,
∴∠AOB=∠OBC,
∵∠FOB=∠AOB,
∴∠FOB=∠OBC,
∴∠OFC=∠FOB+∠OBC=2∠OBC,
∴∠OBC:∠OFC=1:2,是定值;
(3)在△COE和△AOB中,
∵∠OEC=∠OBA,∠C=∠OAB,
∴∠COE=∠AOB,
∴OB、OE、OF是∠AOC的四等分线,
∴∠COE=∠AOC=×80°=20°,
∴∠OEC=180°﹣∠C﹣∠COE=180°﹣100°﹣20°=60°,
故存在某种情况,使∠OEC=∠OBA,此时∠OEC=∠OBA=60°.
8.解:(1)?明同学辅助线的做法为:过点P作PQ∥AB;
(2)如图2,
∵AB∥PQ∥CD,
∴∠1=∠3,∠4=∠2,
∵∠3+∠4=90°,
∴∠1+∠2=90°,
∵∠1=60°,
∴∠2=90°﹣60°=30°,
如图3,
∵AB∥CD,PF∥EQ,
∴∠2=∠3,∠4=∠3,
∵∠1+∠4=90°,
∴∠1+∠2=90°,
∵∠1=60°,
∴∠2=90°﹣60°=30°,
如图4,
∵AB∥CD,PE∥FQ,
∴∠1=∠3,∠4=∠3,
∵∠2+∠4=90°,
∴∠1+∠2=90°,
∵∠1=60°,
∴∠2=90°﹣60°=30°;
(3)设∠CFE=x,∠PEF=∠PDF=y,
过点P作PQ∥AB,
∴∠BEP+∠EPQ=180°,∠CFE=∠FEB=x,
∵AB∥CD,
∴PQ∥CD,
∴∠PDF=∠DPQ,
∴∠DPQ=∠PEF=∠PDF=y,
由∠CFE=∠FEB=x=∠FEP+∠BEP,
∴x=y+(180°﹣α+y),
∴x﹣2y=180°﹣α,
即∠CFE﹣2∠PEF=180°﹣α.
故答案为:(1)过点P作PQ∥AC;(2)30.
9.解:(1)结论:∠BED+∠D=120°,
证明:如图①,延长AB交DE于点F,
∵AB∥CD,
∴∠BFE=∠D,
∵∠ABE=120°,
∴∠BFE+∠BED=∠ABE=120°,
∴∠D+∠BED=120°;
(2)如图②,
∵∠DEF=2∠BEF,∠CDF=∠CDE,
即∠CDE=3∠CDF,
设∠BEF=α,∠CDF=β,
∴∠DEF=2α,∠DEB=3α,∠CDE=3β,∠EDF=2β,
由(1)知:∠BED+∠CDE=120°,
∴3α+3β=120°,
∴α+β=40°,
∴2α+2β=80°,
∴∠EFD=180°﹣∠DEF﹣∠EDF=180°﹣(2α+2β)=180°﹣80°=100°,
答:∠EFD的度数为100°;
(3)如图③,
∵BG⊥AB,
∴∠ABG=90°,
∵∠ABE=120°.
∴∠GBE=∠ABE﹣∠ABG=30°,
∵∠CDE=4∠GDE,
∴∠GDE=∠CDE,
∵∠G+∠GBE=∠E+∠GDE,
∴∠G+30°=∠E+∠CDE,
由(1)知:∠BED+∠CDE=120°,
∴∠CDE=120°﹣∠E,
∴∠G+30°=∠E+(120°﹣∠E),
∴∠G=∠E,
∴=.
10.证明:(1)如图1,过点P作PG∥AB,
,
∵AB∥CD,
∴PG∥CD,
∴∠AEP=∠1,∠CFP=∠2,
又∵∠1+∠2=∠EPF,
∴∠AEP+∠CFP=∠EPF;
(2)如图2,
,
由(1)可得:∠EPF=∠AEP+CFP,∠EQF=∠BEQ+∠DFQ,
∵∠BEP的平分线与∠DFP的平分线相交于点Q,
∴∠EQF=∠BEQ+∠DFQ=(∠BEP+∠DFP)=[360°﹣(∠AEP+∠CFP)]=(360﹣∠EPF),
∴∠EPF+2∠EQF=360°;
(3)由(1)可得:
∠EGF=∠AEG+∠CFG,∠EPF=∠BEP+∠DFP,
∵∠BEP=∠BEG,∠DFP=∠DFG,
∴∠EPF=∠BEP+∠DFP=(∠BEG+∠DFG)=[360°﹣(∠AEG+∠CFG)]=×(360°﹣∠EGF),
∴∠EGF+n∠EPF=360°.
11.解:(1)∠C=∠1+∠2,
证明:过C作l∥MN,如下图所示,
∵l∥MN,
∴∠4=∠2(两直线平行,内错角相等),
∵l∥MN,PQ∥MN,
∴l∥PQ,
∴∠3=∠1(两直线平行,内错角相等),
∴∠3+∠4=∠1+∠2,
∴∠C=∠1+∠2;
(2)
∵∠BDF=∠GDF,
∵∠BDF=∠PDC,
∴∠GDF=∠PDC,
∵∠PDC+∠CDG+∠GDF=180°,
∴∠CDG+2∠PDC=180°,
∴∠PDC=90°﹣∠CDG,
由(1)可得,∠PDC+∠CEM=∠C=90°,
∴∠AEN=∠CEM,
∴=;
(3)
∵BC平分∠PBD,AM平分∠CAD,∠PBC=25°,
∴∠PBD=2∠PBC=50°,∠CAM=∠MAD,
∵PQ∥MN,
∴∠BMA=∠PBD=50°,
∴∠ADB=∠AMB﹣∠MAD=50°﹣∠MAD=50°﹣∠CAM,
由(1)可得,∠ACB=∠PBC+∠CAM,
∴∠ACB+∠ADB=∠PBC+∠CAM+50°﹣∠CAM=25°+50°=75°.
12.证明:∵AB∥GH(已知),
∴∠1=∠3(两直线平行,内错角相等),
又∵CD∥GH(已知),
∴∠4=∠2(两直线平行,内错角相等).
∵AB∥CD(已知),
∴∠BEF+∠EFD=180°(两直线平行,同旁内角互补).
∵EG平分∠BEF(已知),
∴∠1=∠BEF(角平分线定义),
又∵FG平分∠EFD(已知),
∴∠2=∠EFD(角平分线定义),
∴∠1+∠2=(∠BEF+∠EFD),
∴∠1+∠2=90°,
∴∠3+∠4=90°(等量代换),
即∠EGF=90°.
故答案为:两直线平行,内错角相等;∠4=∠2;∠EFD;∠BEF;角平分线定义;角平分线定义;∠BEF;等量代换.
13.解:(1)∠BEC=∠1+∠3.
证明:过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠BEF=∠1,∠CEF=∠3,
∴∠BEC=∠BEF+∠CEF=∠1+∠3;
(2)∠2+∠4=∠1+∠3+∠5.
理由:分别过点E,G,M,作EF∥AB,GH∥AB,MN∥AB,
∵AB∥CD,
∴AB∥CD∥EF∥GH∥MN,
∴∠1=∠BEF,∠FEG=∠EGH,∠HGM=∠GMN,∠CMN=∠5,
∴∠2+∠4=∠BEF+∠FEG+∠GMN+∠CMN=∠1+∠EGH+∠MGH+∠5=∠1+∠3+∠5;
(3)∠2+∠4+∠6=∠1+∠3+∠5+∠7.
理由:分别过点E,G,M,K,P,作EF∥AB,GH∥AB,MN∥AB,KL∥AB,PQ∥AB,
∵AB∥CD,
∴AB∥CD∥EF∥GH∥MN∥KL∥PQ,
∴∠1=∠BEF,∠FEG=∠EGH,∠HGM=∠GMN,∠KMN=∠LKM,∠LKP=∠KPQ,∠QPC=∠7,
∴∠2+∠4+∠6=∠1+∠3+∠5+∠7.
14.解:(1)如图1,过点M作ML∥AB,
∵AB∥CD,
∴ML∥AB∥CD,
∴∠1=∠AEM,∠2=∠CFM,
∵∠EMF=∠1+∠2,
∴∠M=∠AEM+∠CFM.
故答案为:∠M=∠AEM+∠CFM;
(2)如图2,过M作ME'∥AB,
∵AB∥CD,
∴ME'∥CD,
∴∠BEM+∠2=∠DFM+∠4=180°,
∴∠BEM=180°﹣∠2,∠DFM=180°﹣∠4,
∵EN,FN分别平分∠MEB和∠DFM,
∴∠1=∠BEM,∠3=∠DFM,
∴∠1+∠3=(180°﹣∠2)+(180°﹣∠4)=180°﹣×(∠2+∠4)=180°﹣×130°=115°,
∴∠ENF=360°﹣∠1﹣∠3﹣∠E'MF=360°﹣115°﹣130°=115°;
(3)如图3中设∠BEH=x,∠PFG=y,则∠BEM=3x,∠MFG=3y,设EH交CD于K.
∵AB∥CD,
∴∠BEH=∠DKH=x,
∵∠PFG=∠HFK=y,∠DKH=∠H+∠HFK,
∴∠H=x﹣y,
∵∠EMF=α=∠AEM+∠MFG,
∴∠EMF=180°﹣3x+3y=α
∴x﹣y=60°﹣α,
∴∠H=60°﹣α.
15.解:(1)如图1,过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠ABE=∠BEF,∠CDE=∠DEF,
∵BE平分∠ABC,DE平分∠ADC,∠ADC=70°,
∴∠ABC=2∠ABE=2∠BEF,,
∵∠BED=n°,
∴∠BEF=(n﹣35)°,
∴∠ABC=2∠BEF=2(n﹣35)°=(2n﹣70)°;
(2)∠ABC的度数改变,
画出的图形如图2,过点E作EF∥AB,
∵BE平分∠ABC,DE平分∠ADC,∠ADC=70°,
∴∠ABC=2∠ABE,,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠ABE+∠BEF=180°,∠CDE=∠DEF=35°,
∵∠BED=n°,
∴∠BEF=(n﹣35)°,
∴∠ABE=180°﹣∠BEF=180°﹣(n﹣35)°=180°﹣n°+35°=(215﹣n)°,
∴∠ABC=2∠ABE=2(215﹣n)°=(430﹣2n)°.
16.解:(1)如图(1),过K作KG∥AB,交EF于G,
∵AB∥CD,
∴KG∥CD,
∴∠BEK=∠EKG,∠GKF=∠KFD,
∵EK、FK分别为∠BEF与∠EFD的平分线,
∴∠BEK=∠FEK,∠EFK=∠DFK,
∵AB∥CD,
∴∠BEK+∠FEK+∠EFK+∠DFK=180°,即2(∠BEK+∠DFK)=180°,
∴∠BEK+∠DFK=90°,
则∠EKF=∠EKG+∠GKF=90°;
(2)∠K=2∠K1,理由为:
∵∠BEK、∠DFK的平分线相交于点K1,
∴∠BEK1=∠KEK1,∠KFK1=∠DFK1,
∵∠BEK+∠FEK+∠EFK+∠DFK=180°,即2(∠BEK+∠KFD)=180°,
∴∠BEK+∠KFD=90°,即∠BEK1+∠DFK1=45°,
同理得∠K1=∠BEK1+∠DFK1=45°,
则∠K=2∠K1;
(3)如图(3),
根据(2)中的规律可得:∠K2=∠K1=22.5°,∠K3=∠K2=11.25°,∠K4=∠K3=5.625°.
17.解:∵∠B=∠D=90°,
∴∠DAB+∠BCD=180°,
∵EA∥CF,
∴∠3=∠1,
∵∠3+∠4=90°,
∴∠1+∠4=90°,
∴∠2+∠5=90°,
∵AE平分∠BAD交CD于点E,
∴∠4=∠6,
∴∠4=∠5,
∴∠1=∠2,
∴CF平分∠BCD.
18.解:(1)过E作EF∥AB,
∵AB∥CD,
∴EF∥CD,
∵∠B=15°,
∴∠BEF=15°,
又∵∠BED=90°,
∴∠DEF=75°,
∵EF∥CD,
∴∠D=75°,
故答案为:75°;
(2)过E作EF∥AB,
∵AB∥CD,
∴EF∥CD,
∴∠B+∠BEF+∠DEF+∠D=360°,
又∵∠B=α,∠D=β,
∴∠BED=∠BEF+∠DEF=360°﹣α﹣β,
故答案为:∠BED=360°﹣α﹣β;
(3)猜想:∠BEC=180°﹣α+β.
证明:过点E作EF∥AB,
则∠BEF=180°﹣∠B=180°﹣α,
∵AB∥EF,AB∥CD,
∴EF∥CD,
∴∠CEF=∠C=β,
∴∠BEC=∠BEF+∠CEF=180°﹣α+β.
19.解:(1)过P作PM∥AB,过Q作QN∥AB,
∵AB∥CD,
∴AB∥CD∥PM,AB∥CD∥QN,
∴∠BEP=∠MPE,∠DFP=∠MPF,∠BEQ=∠NQE,∠DFQ=∠FQN,
∴∠BEP+∠DFP=∠MPE+∠MPF=∠EPF=110°,∠BEQ+∠DFQ=∠NQE+∠NQF=∠EQF,
∵QE,QF分别平分∠PEB和∠PFD,
∴∠BEQ+∠DFQ=(∠BEP+∠DFP)=;
猜想:∠EPF与∠EQF的数量关系为∠EPF=2∠EQF.理由如下:
∵AB∥CD,
∴AB∥CD∥PM,AB∥CD∥QN,
∴∠BEP=∠MPE,∠DFP=∠MPF,∠BEQ=∠NQE,∠DFQ=∠FQN,
∴∠BEP+∠DFP=∠MPE+∠MPF=∠EPF,∠BEQ+∠DFQ=∠NQE+∠NQF=∠EQF,
∵QE,QF分别平分∠PEB和∠PFD,
∴2(∠BEQ+∠DFQ)=∠BEP+∠DFP=∠EPF,
即∠EPF=2∠EQF;
故答案为55°;
(2)2∠EQF+∠EPF=360°.理由如下:
如图2,过P作PM∥AB,过Q作QN∥AB,
∵AB∥CD,
∴AB∥CD∥PM,AB∥CD∥QN,
∴∠BEP+∠MPE=180°,∠DFP+∠MPF=180°,∠BEQ=∠NQE,∠DFQ=∠FQN,
∴∠BEP+∠DFP+∠MPE+∠MPF=360°即∠BEP+∠DFP+∠EPF=360°,∠EQF∠BEQ+∠DFQ=∠NQE+∠NQF=∠EQF,
∵QE,QF分别平分∠PEB和∠PFD,
∴∠BEQ+∠DFQ=(∠BEP+∠DFP)=∠EQF,即∠BEP+∠DFP=2∠EQF,
∴2∠EQF+∠EPF=360°;
(3)当点P在EF的左侧,
根据(1)的方法可得∠Q1=(∠BEP+∠DFP)=∠EQF,
∠Q2=(∠BEP+∠DFP)=∠EQF,
…
则∠Qn=()n(∠BEP+∠DFP)=()n∠EQF,
∵2∠EQF+∠EPF=360°,∠BEP+∠DFP=2∠EQF,
∴∠EPF+2n+1?∠EQnF=360°.
当点P在EF的右侧,同理可求∠EPF=2n+1∠EQnF.
20.解:①∵AB∥CD,∠α=50°
∴∠2=∠α=50°,
故答案为50;
(2)∠α=∠1+∠2.
证明:过P作PG∥AB,
∵AB∥CD,
∴PG∥AB∥CD,
∴∠2=∠EPG,∠1=∠FPG,
∵∠α=∠EPF=∠EPG+∠FPG,
∴∠α=∠1+∠2;
(3)不成立.
理由:过P作PH∥AB,
∵AB∥CD,
∴PH∥AB∥CD,
∴∠2=∠EPH,∠1=∠FPH,
∵∠α=∠EPF=∠EPH﹣∠FPH,
∴∠α=∠2﹣∠1,
故不成立.
21.(1)证明:如图1,过点P作PG∥AB,
,
∵AB∥CD,
∴PG∥CD,
∴∠AEP=∠1,∠CFP=∠2,
又∵∠1+∠2=∠EPF,
∴∠AEP+∠CFP=∠EPF;
(2)如图2,
,
由(1)可得:∠EPF=∠AEP+CFP,∠EQF=∠BEQ+∠DFQ,
∵∠BEP的平分线与∠DFP的平分线相交于点Q,
∴∠EQF=∠BEQ+∠DFQ=(∠BEP+∠DFP)=[360°﹣(∠AEP+∠CFP)]=(360﹣∠EPF),
∴∠EPF+2∠EQF=360°;
(3)由(1)可得:∠P=∠AEP+CFP,∠Q=∠BEQ+∠DFQ,
∵∠BEQ=∠BEP,∠DFQ=∠DFP,
∴∠Q=∠BEQ+∠DFQ=(∠BEP+∠DFP)=[360°﹣(∠AEP+∠CFP)]=×(360°﹣∠P),
∴∠P+n∠Q=360°;
故答案为:∠P+n∠Q=360°.
22.解:(1)如图1,过点G作GH∥AB,
∵AB∥CD,
∴GH∥AB∥CD,
∴∠AMG=∠HGM,∠CNG=∠HGN,
∵GM⊥GN,
∴∠MGN=∠MGH+∠HGN=∠AMG+∠CNG=90°;
答:∠AMG+∠CNG的度数为90°;
(2)如图2,过过点G作GK∥AB,过点P作PQ∥AB,设∠GND=α,
∵GK∥AB,AB∥CD,
∴GK∥CD,
∴∠KGN=∠GND=α,
∵GK∥AB,∠BMG=40°,
∴∠MGK=∠BMG=40°,
∵MG平分∠BMP,
∴∠GMP=∠BMG=40°,
∴∠BMP=80°,
∵ND平分∠GNP,
∴∠DNP=∠GND=α,
∵AB∥CD,
∴PQ∥CD,
∴∠QPN=∠DNP=α,
∴∠MGN=40°+α,∠MPN=80°﹣α,
∴∠MGN+∠MPN=40°+α+80°﹣α=120°.
23.解:(1)作PE∥AB,
∵AB∥CD,AB∥PE,
∴CD∥PE,
∴∠APE=∠A,∠CPE=∠DCP,
∴∠APC=∠APE+∠CPE=∠BAP+∠DCP.
故答案为∠APC=∠BAP+∠DCP.
(2)①作图如图1:
设∠DCP=β,
由(1)可得,∠APC=α+β,
∵AK平分∠BAP,
∴∠BAK=∠BAP=α,
同理,∠LCD=(180°﹣β)=90°﹣β,
过点Q作QM∥AB,如图2,则∠MQK=∠BAK=,
∵AB∥CD,
∴QM∥CD,
∴,
∴;
②∵AP∥QC,
∴∠AQC=∠KAP,
由①得,∠AQC=90°﹣(α+β),
∴,
整理得,β=180°﹣2β,即∠DCP=180°﹣2β.
24.解:(1)∠1=∠2,
理由:如图1,
∵AB∥EF,
∴∠3=∠2,
∵BC∥DE,
∴∠3=∠1,
∴∠1=∠2;
(2)∠1+∠2=180°,
理由:如图2,
∵AB∥EF,
∴∠3+∠2=180°,
∵BC∥DE,
∴∠3=∠1,
∴∠1+∠2=180°.
(3)如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.
故答案为:一个角的两边与另一个角的两边分别平行,这两个角相等或互补;
(4)设另一个角为x°,根据以上结论得:
2x﹣60=x或2x﹣60+x=180,
解得:x=60,或x=80,
故答案为:60°、60°或80°,100°.
25.解:(1)如图1中,过点E作EG∥AB,
则∠BEG=∠ABE,
因为AB∥CD,EG∥AB,
所以CD∥EG,
所以∠DEG=∠CDE,
所以∠BEG+∠DEG=∠ABE+∠CDE,
即∠BED=∠ABE+∠CDE;
(2)图2中,因为BF平分∠ABE,
所以∠ABE=2∠ABF,
因为DF平分∠CDE,
所以∠CDE=2∠CDF,
所以∠ABE+∠CDE=2∠ABF+2∠CDF=2(∠ABF+∠CDF),
由(1)得:因为AB∥CD,
所以∠BED=∠ABE+∠CDE,
∠BFD=∠ABF+∠CDF,
所以∠BED=2∠BFD.
(3)∠BED=360°﹣2∠BFD.
图3中,过点E作EG∥AB,
则∠BEG+∠ABE=180°,
因为AB∥CD,EG∥AB,
所以CD∥EG,
所以∠DEG+∠CDE=180°,
所以∠BEG+∠DEG=360°﹣(∠ABE+∠CDE),
即∠BED=360°﹣(∠ABE+∠CDE),
因为BF平分∠ABE,
所以∠ABE=2∠ABF,
因为DF平分∠CDE,
所以∠CDE=2∠CDF,
∠BED=360°﹣2(∠ABF+∠CDF),
由(1)得:因为AB∥CD,
所以∠BFD=∠ABF+∠CDF,
所以∠BED=360°﹣2∠BFD.
26.证明:∵∠ABC+∠ECB=180°(已知),
∴AB∥DE(同旁内角互补,两直线平行).
∴∠ABC=∠BCD(两直线平行,内错角相等).
∵∠P=∠Q(已知),
∴PB∥(CQ)(内错角相等,两直线平行).
∴∠PBC=(∠BCQ)(两直线平行,内错角相等).
∵∠1=∠ABC﹣(∠PBC),∠2=∠BCD﹣(∠BCQ),
∴∠1=∠2(等量代换).
故答案为:同旁内角互补,两直线平行;两直线平行,内错角相等;CQ,内错角相等,两直线平行;∠BCQ;∠PBC;∠BCQ.
27.(1)证明:∵AC∥BD,
∴∠DAE=∠BDA,
∵∠BDA=∠C,
∴∠DAE=∠C,
∴AD∥BC;
(2)证明:如图2,设CE与BD相交于点G,∠BGA=∠BDA+DAE,
∵BD⊥BC,
∴∠BGA+∠C=90°,
∴∠BDA+∠DAE+∠C=90°,
∵∠BDA=∠C,
∴∠DAE+2∠C=90°;
(3)如图3,设∠DAE=α,则∠DFE=8α,
∵∠DFE+∠AFD=180°,
∴∠AFD=180°﹣8α,
∵DF∥BC,
∴∠C=∠AFD=180°﹣8α,
又∵2∠C+∠DAE=90°,
∴2(180°﹣8α)+α=90°,
∴α=18°,
∴∠C=180°﹣8α=36°=∠ADB,
又∵∠C=∠BDA,∠BAC=∠BAD,
∴∠ABC=∠ABD=∠CBD=45°,
△ABD中,∠BAD=180°﹣45°﹣36°=99°.
答:∠BAD的度数是99°.
28.证明:∵AD∥BC,
∴∠2=∠E,
∵AE平分∠BAD,
∴∠1=∠2,
∴∠1=∠E,
∵∠CFE=∠E,
∴∠1=∠CFE,
∴AB∥DC.
29.解:(1)①由条件可知:∠1与∠3的大小关系是相等,理由是两直线平行,同位角相等;∠2与∠4的大小关系是相等;
②反射光线BC与EF的位置关系是平行,理由是同位角相等,两直线平行;
故答案为:①相等、两直线平行,同位角相等、相等;②平行、同位角相等,两直线平行.
(2)如图,
∵∠1=40°,
∴∠4=∠1=40°,
∴∠6=180°﹣40°﹣40°=100°,
∵m∥n,
∴∠2+∠6=180°,
∴∠2=80°,
∴∠5=∠7==50°,
∴∠3=180°﹣50°﹣40°=90°.
30.证明:∵AB∥CD,
∴∠1=∠ACD,
∵∠1=∠2,
∴∠2=∠ACD,
∴∠2+∠CAE=∠ACD+∠CAE,
∴∠DAC=∠4,
∵∠3=∠4,
∴∠DAC=∠3,
∴AD∥BE.
31.解:(1)∠PEQ=∠APE+∠CQE,理由如下:
∵AB∥CD,EH∥AB,
∴AB∥EH∥CD,
∴∠APE=∠PEH,∠CQE=∠QEH.
∵∠PEQ=∠PEH+∠QEH,
∴∠PEQ=∠APE+∠CQE.
(2)∠APE+∠CQE+∠PEQ=360°;理由如下:
过点E作EG∥AB,如图2所示:
∵AB∥CD,EG∥AB,
∴AB∥EG∥CD,
∴∠APE+∠PEG=180°,∠CQE+∠QEG=180°,
∴∠APE+∠PEG+∠CQE+∠QEG=360°,
即∠APE+∠CQE+∠PEQ=360°;
(3)由(2)得:∠PEQ+∠BPE+∠EQD=360°,
∵∠PEQ=140°,
∴∠BPE+∠EQD=360°﹣140°=220°,
∵PF平分∠BPE,QF平分∠EQD,
∴∠BPF=∠BPE,∠DQF=∠EQD,
∴∠BPF+∠DQF=(∠BPE+∠EQD)=110°,
由(1)得:∠PFQ=∠BPF+∠DQF=110°.
32.解:AB∥CD.
理由如下:作BE⊥NB,CF⊥NC,如图,
∵∠1=∠2,∠3=∠4,BE∥NC,
∴∠2=∠NCB,
∴∠2+∠3=∠1+∠4=90°,
∴∠ABC+∠BCD=180°,
∴AB∥CD.
33.解:(1)过点E、F分别作EM∥AB,FN∥AB,如图2所示:
∵EM∥AB,
∴∠1=∠B,
又∵FN∥AB,
∴FN∥EM,
∴∠2=∠3,
又∵AB∥CD,
∴FN∥CD,
∴∠4+∠C=180°,
又∵∠BEF=∠1+∠2,∠EFC=∠3+∠4,∠BEF=60°
∴∠B+∠EFC+∠C=∠1+∠3+∠4+∠C
=(∠1+∠2)+(∠4+∠C)
=60°+180°
=240°;
(2)过点G、H作EF∥AB,MN∥AB,如图3所示:
∵BE平分∠ABG,CF平分∠DCG,
∴∠ABG=2∠1,∠DCG=2∠4,
又∵EF∥AB,
∴2∠1+∠7=180°,
又∵AB∥CD,
∴EF∥CD,
∴2∠4+∠8=180°,
∴∠7+∠8=360°﹣2(∠1+∠4),
又∵∠7+∠8+∠BGC=180°,
∴2(∠1+∠4)=∠BGC+180°,
又∵MN∥AB,
∴∠1=∠5,
又∵AB∥CD,
∴MN∥CD,
∴∠4=∠6,
∴2(∠5+∠6)=∠BGC+180°,
又∵∠5+∠6+∠BHC=180°,
∴∠BGC+2∠BHC=180°,
又∠BGC=∠BHC+27°,
∴3∠BHC+27°=180°,
∴∠BHC=51°;
故答案为:240°,51°.
34.解:(1)∵AM∥BN,
∴∠MAB+∠2=180°,
∵∠MAB+∠1+∠BAC=180°,∠1=∠BAC,∠1=35°,
∴∠2=2∠1=70°,
∵∠2+∠ABC+∠NBF=180°,∠ABC=∠NBF,
∴∠ABC=55°,
∴∠3=180°﹣∠BAC﹣∠ABC=90°;
当∠1=50°时,
同理可得,∠2=100°,∠ABC=40°,∠BAC=∠1=50°,
则∠3=180°﹣∠BAC﹣∠ABC=90°;
故答案为:70°,90°,90°;
(2)猜想:当两平面镜CE,CF的夹角∠3为90°时,可以使任何射到平面镜CE上的光线MA,经过平面镜CE,CF的两次反射后,入射光线MA与反射光线BN平行.
理由:∵∠3=90°,
∴∠BAC+∠ABC=90°,
∵∠1=∠BAC,∠ABC=∠NBF,
∴∠BAC+∠1+∠ABC+∠NBF=180°,
∴∠MAB+∠2=180°,
∴MA∥BN.
35.解:感知与填空:过点E作直线EF∥CD,
∴∠2=∠D(两直线平行,内错角相等),
∵AB∥CD(已知),EF∥CD,
∴AB∥EF(两直线都和第三条直线平行,那么这两条直线也互相平行),
∴∠B=∠1(两直线平行,内错角相等),
∵∠1+∠2=∠BED,
∴∠B+∠D=∠BED(等量代换),
故答案为:两直线平行,内错角相等;两直线都和第三条直线平行,那么这两条直线也互相平行;两直线平行,内错角相等;等量代换.
应用与拓展:过点G作GN∥AB,
则GN∥CD,如图②所示:
由感知与填空得:∠E=∠B+∠EGN,∠F=∠D+∠FGN,
∴∠E+∠F=∠B+∠EGN+∠D+∠FGN=∠B+∠D+∠EGF=22°+25°+35°=82°,
故答案为:82.
方法与实践:设AB交EF于M,如图③所示:
∠AME=∠FMB=180°﹣∠F﹣∠B=180°﹣80°﹣60°=40°,
由感知与填空得:∠E=∠D+∠AME,
∴∠D=∠E﹣∠AME=60°﹣40°=20°,
故答案为:20.
36.解:(1)过点P作EF∥AB,
∴∠B+∠BPE=180°,
∵AB∥CD,EF∥AB,
∴CD∥EF(如果两条直线都和第三条直线平行,那么这两条直线也互相平行),
∴∠EPD+∠D=180°,
∴∠B+∠BPE+∠EPD+∠D=360°,
∴∠B+∠BPD+∠D=360°,
故答案为:CD∥EF,∠D;
(2)猜想∠BPD=∠B+∠D,
理由:过点P作EP∥AB,
∵EP∥AB,
∴∠B=∠BPE(两直线平行,内错角相等),
∵AB∥CD,EP∥AB,
∴CD∥EP(如果两条直线都和第三条直线平行,那么这两条直线也互相平行),
∴∠EPD=∠D,
∴∠BPD=∠B+∠D;
(3)图③结论:∠D=∠BPD+∠B,
理由是:过点P作EP∥AB,
∵EP∥AB,
∴∠B=∠BPE(两直线平行,内错角相等),
∵AB∥CD,EP∥AB,
∴CD∥EP(如果两条直线都和第三条直线平行,那么这两条直线也互相平行),
∴∠EPD=∠D,
∴∠D=∠BPD+∠B;
图④结论∠B=∠BPD+∠D,
理由是:∵EP∥AB,
∴∠B=∠BPE(两直线平行,内错角相等),
∵AB∥CD,EP∥AB,
∴CD∥EP(如果两条直线都和第三条直线平行,那么这两条直线也互相平行),
∴∠EPD=∠D,
∴∠B=∠BPD+∠D.
37.证明:∵∠1=∠2
(已知)
又∵∠1=∠3
(对顶角相等
)
∴∠2=∠3
(等量代换)
∴CE∥FDB(
同位角相等,两直线平行
)
∴∠B=∠CEA
(两直线平行,同位角相等
)
∵∠B=∠C
(已知)
∴∠C=∠CEA
(等量代换)
∴AB∥CD
(内错角相等,两直线平行
)
∴∠A=∠D.(
两直线平行,内错角相等
)
38.解:BF与AC的位置关系是:BF⊥AC.
理由:∵∠AGF=∠ABC,
∴BC∥GF,
∴∠1=∠3;
又∵∠1+∠2=180°,
∴∠2+∠3=180°,
∴BF∥DE;
∵DE⊥AC,
∴BF⊥AC.
39.证明:∵∠3=∠4,
∴CF∥BD,
∴∠5=∠FAB;
∵∠5=∠6,
∴∠6=∠FAB,
∴AB∥CD,
∴∠2=∠EGA;
∵∠1=∠2,
∴∠1=∠EGA,
∴ED∥FB
1.如图,若直线a∥b,那么∠x=( )
A.64°
B.68°
C.69°
D.66°
2.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,则两次拐弯的角度可以是( )
A.第一次向右拐40°第二次向左拐140°
B.第一次向左拐40°第二次向右拐40°C.第一次向左拐40°第二次向右拐140°
D.第一次向右拐40°第二次向右拐40°
3.小张同学观察如图1所示的北斗七星图,小张同学把北斗七星:摇光、开阳、玉衡、天权、天玑、天璇、天枢按图2分别标为点A,B,C,D,E,F,G,然后将点A,B,C,D,E,F,G顺次首尾连接,发现AG恰好经过点C,且∠B﹣∠DCG=115°,∠B﹣∠D=10°,若AG∥EF,则∠E=m°,这里的m=
.
4.如图,一束光线从点C出发,经过平面镜AB反射后,沿与AF平行的线段DE射出(此时∠1=∠2),若测得∠DCF=100°,则∠A=
.
5.如图,已知直线AB∥CD,MN分别交AB,CD于点E,F,∠BEF与∠DFE的两条平分线相交于点P1,∠BEP1与∠DFP1的两条平分线相交于点P2,则∠P2的度数为
.
6.如图1,已知∠ACB=80°,点A在直线EF上,点B在直线GH上,且∠CAE+∠CBG=80°.
(1)试判断直线EF与GH的位置关系,并说明理由;
(2)如图2,若点B在直线GH上运动,作∠CAP=2∠CAE,作∠CBP=2∠CBG,试判断∠APB的大小是否会随着点B的运动而发生变化?若不变,求出∠APB的大小;若变化,请说明理由.
7.如图,直线CB∥OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值.
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.
8.阅读下?材料,完成(1)~(3)题.
数学课上,?师出示了这样?道题:
如图1,已知AB∥CD,点E,F分别在AB,CD上,EP⊥FP,∠1=60°.求∠2的度数.
同学们经过思考后,?明、?伟、?华三位同学?不同的?法添加辅助线,交流了??的想法:
?明:“如图2,通过作平?线,发现∠1=∠3,∠2=∠4,由已知EP⊥FP,可以求出∠2的度数.”
?伟:“如图3这样作平?线,经过推理,得∠2=∠3=∠4,也能求出∠2的度数.”
?华:“如图4,也能求出∠2的度数.”
(1)请你根据?明同学所画的图形(图2),描述?明同学辅助线的做法,辅助线:
;
(2)请你根据以上同学所画的图形,直接写出∠2的度数为
°;
?师:“这三位同学解法的共同点,都是过?点作平?线来解决问题,这个?法可以推?.”
请?家参考这三位同学的?法,使?与他们类似的?法,解决下?的问题:
(3)如图5,AB∥CD,点E,F分别在AB,CD上,FP平分∠EFD,∠PEF=∠PDF,若∠EPD=α,请探究∠CFE与∠PEF的数量关系(?含α的式?表示),并验证你的结论.
9.如图,AB∥CD,∠ABE=120°.
(1)如图①,写出∠BED与∠D的数量关系,并证明你的结论;
(2)如图②,∠DEF=2∠BEF,∠CDF=∠CDE,EF与DF交于点F,求∠EFD的度数;
(3)如图③,过B作BG⊥AB于G点,∠CDE=4∠GDE,求的值.
10.如图1,AB∥CD,在AB、CD内有一条折线EPF.
(1)求证:∠AEP+∠CFP=∠EPF;
(2)在图2中,画∠BEP的平分线与∠DFP的平分线,两条角平分线交于点Q,请你补全图形,试探索∠EPF与∠EQF之间的关系,并证明你的结论;
(3)在(2)的条件下,已知∠BEP和∠DFP均为钝角,点G在直线AB、CD之间,且满足∠BEG=∠BEP,∠DFG=∠DFP,(其中n为常数且n>1),直接写出∠EGF与∠EPF的数量关系.
11.如图,直线PQ∥MN,点C是PQ、MN之间(不在直线PQ,MN上)的一个动点.
(1)如图1,若∠1与∠2都是锐角,请写出∠C与∠1,∠2之间的数量关系并说明理由.
(2)把Rt△ABC如图2摆放,直角顶点C在两条平行线之间,CB与PQ交于点D,CA与MN交于点E,BA与PQ交于点F,点G在线段CE上,连接DG,有∠BDF=∠GDF,求的值.
(3)如图3,若点D是MN下方一点,BC平分∠PBD,AM平分∠CAD,已知∠PBC=25°,求∠ACB+∠ADB的度数.
12.阅读下列推理过程,在括号中填写理由.
如图,AB∥CD∥GH,EG平分∠BEF,FG平分∠EFD,求证:∠EGF=90°.
证明:∵AB∥GH(已知),
∴∠1=∠3(
),
又∵CD∥GH(已知),
∴
(两直线平行,内错角相等).
∵AB∥CD(已知),
∴∠BEF+
=180°(两直线平行,同旁内角互补).
∵EG平分∠BEF(已知),
∴∠1=
(
),
又∵FG平分∠EFD(已知),
∴∠2=∠EFD(
),
∴∠1+∠2=(
+∠EFD),
∴∠1+∠2=90°,
∴∠3+∠4=90°(
),即∠EGF=90°.
13.(1)如图甲,AB∥CD,∠BEC与∠1+∠3的关系是什么?并写出推理过程;
(2)如图乙,AB∥CD,直接写出∠2+∠4与∠1+∠3+∠5的数量关系
;
(3)如图丙,AB∥CD,直接写出∠2+∠4+∠6与∠1+∠3+∠5+∠7的数量关系
.
14.已知:直线AB∥CD,点E,F分别在直线AB,CD上,点M为两平行线内部一点.
(1)如图1,∠AEM,∠M,∠CFM的数量关系为
;(直接写出答案)
(2)如图2,∠MEB和∠MFD的角平分线交于点N,若∠EMF等于130°,求∠ENF的度数;
(3)如图3,点G为直线CD上一点,延长GM交直线AB于点Q,点P为MG上一点,射线PF、EH相交于点H,满足∠PFG=∠MFG,∠BEH=∠BEM,设∠EMF=α,求∠H的度数(用含α的代数式表示).
15.如图,AB∥CD,点C在点D的右侧,∠ABC,∠ADC的平分线交于点E(不与B,D点重合),∠ADC=70°.设∠BED=n°.
(1)若点B在点A的左侧,求∠ABC的度数;(用含n的代数式表示)
(2)将(1)中的线段BC沿DC方向平移,当点B移动到点A右侧时,请画出图形并判断∠ABC的度数是否改变.若改变,请求出∠ABC的度数(用含n的代数式表示);若不变,请说明理由.
16.如图所示,直线AB∥CD,直线EF分别交AB、CD于E、F两点,∠BEF、∠DFE的平分线相交于点K.
(1)求∠EKF的度数;
(2)如图(2)所示,作∠BEK、∠DFK的平分线相交于点K1,问∠K1与∠K的度数是否存在某种特定的等量关系?写出结论并证明.
(3)在图(2)中作∠BEK1、∠DFK1的平分线相交于点K2,作∠BEK2、∠DFK2的平分线相交于点K3,依此类推,……,请直接写出∠K4的度数.
17.如图所示,四边形ABCD中,AE平分∠DAB,AE∥CF,∠B=∠D=90°.求证:CF平分∠BCD.
18.直线AB∥CD,E为直线AB、CD之间的一点,完成以下问题:
(1)如图1,若∠B=15°,∠BED=90°,则∠D=
;
(2)如图2,若∠B=α,∠D=β,求出∠BED的度数(用a、β表示);
(3)如图3,若∠B=α,∠C=β,则a、β与∠BEC之间有什么等量关系?请猜想证明.
19.如图,AB∥CD,定点E,F分别在直线AB,CD上,在平行线AB,CD之间有一动点P,且满足0°<∠EPF<180°,QE,QF分别平分∠PEB和∠PFD.
在探究∠EPF与∠EQF之间的数量关系时,我们需要对点P的位置进行分类讨论:
(1)如图1,当P点在EF的右侧时,若∠EPF=110°,则∠EQF=
;
猜想∠EPF与∠EQF的数量关系,请直接写出结果;
(2)如图2,当P点在EF的左侧时,探究∠EPF与∠EQF的数量关系,请说明理由;
(3)若∠BEQ与∠DFQ的角平分线交于点Q1,∠BEQ1与∠DFQ1的角平分线交于点Q2,∠BEQ2与∠DFQ2的角平分线交于点Q3;…以此类推,则∠EPF与∠EQnF满足怎样的数量关系?(直接写出结果)
20.直线AB、CD被直线EF所截,AB∥CD,点P是平面内一动点.
(1)若点P在直线CD上,如图①,∠α=50°,则∠2=
°.
(2)若点P在直线AB、CD之间,如图②,试猜想∠α、∠1、∠2之间的等量关系并给出证明;
(3)若点P在直线CD的下方,如图③,(2)中∠α、∠1、∠2之间的关系还成立吗?请作出判断并说明理由.
21.如图1,AB∥CD,在AB、CD内有一条折线EPF.
(1)求证:∠AEP+∠CFP=∠EPF;
(2)如图2,已知∠BEP的平分线与∠DFP的平分线相交于点Q,试探索∠EPF与∠EQF之间的关系.
(3)已知∠BEQ=∠BEP,∠DFQ=∠DFP,有∠P与∠Q的关系为
.(直接写结论)
22.综合探究:
已知,AB∥CD,点M、N分别是AB、CD上两点,点G在AB、CD之间,连接MG、NG.
(1)如图1,若GM⊥GN,求∠AMG+∠CNG的度数;
(2)如图2,若点P是CD下方一点,MG平分∠BMP,ND平分∠GNP,已知∠BMG=40°,求∠MGN+∠MPN的度数.
23.如图,已知AB∥CD,点P是AB、CD之间的任意一点且在AC右侧.
(1)∠APC与∠BAP、∠DCP的数量关系是
;
(2)∠BAP的平分线所在直线与∠DCP的邻补角平分线相交于点Q,∠BAP=α.
①根据题意,在图中补全图形,判断∠APC与∠AQC的数量关系并说明理由;
②若AP∥CQ,求∠DCP的度数(用含α的式子表示).
24.已知一个角的两边与另一个角的两边分别平行,结合图,试探索这两个角之间的关系,并说明你的结论.
(1)如图1,AB∥EF,BC∥DE,∠1与∠2有何关系?说明理由;
(2)如图2,AB∥EF,BC∥DE,∠1与∠2有何关系?说明理由;
(3)由(1)(2)你能得出的结论是:如果
,那么
;
(4)若两个角的两边分别平行,且一个角比另一个角的2倍少60°,则这两个角度数的分别是
.
25.已知AB∥CD,点E在AB与CD之间.
(1)图1中,试说明:∠BED=∠ABE+∠CDE;
(2)图2中,∠ABE的平分线与∠CDE的平分线相交于点F,请利用(1)的结论说明:∠BED=2∠BFD.
(3)图3中,∠ABE的平分线与∠CDE的平分线相交于点F,请直接写出∠BED与∠BFD之间的数量关系.
26.如图,∠ABC+∠ECB=180°,∠P=∠Q.求证:∠1=∠2.
在下列解答中,填空:
证明:∵∠ABC+∠ECB=180°(已知),
∴AB∥DE(
).
∴∠ABC=∠BCD(
).
∵∠P=∠Q(已知),
∴PB∥(
)(
).
∴∠PBC=(
)(两直线平行,内错角相等).
∵∠1=∠ABC﹣(
),∠2=∠BCD﹣(
),
∴∠1=∠2(等量代换).
27.已知点A在射线CE上,∠BDA=∠C.
(1)如图1,若AC∥BD,求证:AD∥BC;
(2)如图2,若∠BAC=∠BAD,BD⊥BC,请证明∠DAE+2∠C=90°;
(3)如图3,在(2)的条件下,过点D作DF∥BC交射线CE于点F,当∠DFE=8∠DAE时,求∠BAD的度数.(直接写出结果)
28.如图,已知AD∥BC,AE平分∠BAD交BC延长线于点E,CD与AE相交于点F,∠CFE=∠E,求证:AB∥DC.
29.(1)阅读并回答:
科学实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的角相等.如图1,一束平行光线AB与DE射向一个水平镜面后被反射,此时∠1=∠2,∠3=∠4.
①由条件可知:∠1与∠3的大小关系是
,理由是
;∠2与∠4的大小关系是
;
②反射光线BC与EF的位置关系是
,理由是
.
(2)解决问题:
如图2.一束光线m射到平面镜a上,被a反射到平面镜b上,又被b镜反射,若b反射出的光线n平行于m,且∠1=40°,求∠2和∠3的度数.
30.已知:如图,点B,C,E在一条直线上,点A、E、F在一条直线上,AB∥CD,∠1=∠2,∠3=∠4.求证:AD∥BE.
31.某学习小组发现一个结论:已知直线a∥b,若直线c∥a,则c∥b.他们发现这个结论运用很广,请你利用这个结论解决以下问题:
已知直线AB∥CD,点E在AB、CD之间,点P、Q分别在直线AB、CD上,连接PE、EQ.
(1)如图1,过点E作EH∥AB,运用上述结论,探究∠PEQ、∠APE、∠CQE之间的数量关系,并说明理由;
(2)如图2,类比(1)中的方法,运用上述结论,探究∠PEQ、∠APE、∠CQE之间的数量关系,并说明理由;
(3)如图3,PF平分∠BPE,QF平分∠EQD,当∠PEQ=140°时,直接写出∠PFQ的度数.
32.实验证明:平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.如图有两块互相垂直的平面镜MN、NP.一束光线AB射在其中一块MN上,经另外一块NP反射.两束光线会平行吗?若不平行,请说明理由,若平行,请给予证明.
33.请阅读小明同学在学习平行线这章知识点时的一段笔记,然后解决问题.
小明:老师说在解决有关平行线的问题时,如果无法直接得到角的关系,就需要借助辅助线来帮助解答,今天老师介绍了一个“美味”的模型﹣﹣﹣“猪蹄模型”.即
已知:如图1,AB∥CD,E为AB、CD之间一点,连接AE,CE得到∠AEC.
求证:∠AEC=∠A+∠C.
小明笔记上写出的证明过程如下:
证明:过点E作EF∥AB,
∴∠1=∠A.
∵AB∥CD,EF∥AB,
∴EF∥CD.
∴∠2=∠C.
∵∠AEC=∠1+∠2,
∴∠AEC=∠A+∠C.
请你利用“猪蹄模型”得到的结论或解题方法,完成下面的两个问题.
(1)如图2,若AB∥CD,∠E=60°,则∠B+∠C+∠F=
.
(2)如图3,AB∥CD,BE平分∠ABG,CF平分∠DCG,∠G=∠H+27°,则∠H=
.
34.实验证明,平面镜反射光线的规律是:照射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.
(1)如图,一束光线MA照射到平面镜CE上,被CE反射到平面镜CF上,又被CF反射.已知被CF反射出的光线BN与光线MA平行.若∠1=35°,则∠2=
,∠3=
;若∠1=50°,∠3=
.
(2)由(1)猜想:当两平面镜CE,CF的夹角∠3为多少度时,可以使任何射到平面镜CE上的光线MA,经过平面镜CE,CF的两次反射后,入射光线MA与反射光线BN平行,请你写出推理过程.
35.感知与填空:如图①,直线AB∥CD.求证:∠B+∠D=∠BED.
阅读下面的解答过程,井填上适当的理由.
解:过点E作直线EF∥CD
∴∠2=∠D(
)
∵AB∥CD(已知),EF∥CD,
∴AB∥EF(
)
∴∠B=∠1(
)
∵∠1+∠2=∠BED,
∴∠B+∠D=∠BED(
)
应用与拓展:如图②,直线AB∥CD.若∠B=22°,∠G=35°,∠D=25°,则∠E+∠F=
度.
方法与实践:如图③,直线AB∥CD.若∠E=∠B=60°,∠F=80°,则∠D=
度.
36.如图(1),AB∥CD,试求∠BPD与∠B、∠D的数量关系,说明理由.
(1)填空:
解:过点P作EF∥AB,
∴∠B+∠BPE=180°
∵AB∥CD,EF∥AB
∴
(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∠EPD+
=180°
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
(2)依照上面的解题方法,观察图(2),已知AB∥CD,猜想图中的∠BPD与∠B、∠D的数量关系,并说明理由.
(3)观察图(3)和(4),已知AB∥CD,直接写出图中的∠BPD与∠B、∠D的数量关系,不用说明理由.
37.已知:如图,∠1=∠2,∠B=∠C,求证:∠A=∠D.
38.已知如图,DE⊥AC,∠AGF=∠ABC,∠1+∠2=180°,试判断BF与AC的位置关系,并说明理由.
39.已知:如图,∠1=∠2,∠3=∠4,∠5=∠6.求证:ED∥FB
参考答案
1.解:令与130°互补的角为∠1,如图所示.
∵∠1+130°=180°,
∴∠1=50°.
∵a∥b,
∴x+48°+20°=∠1+30°+52°,
∴x=64°.
故选:A.
2.解:A、如图1:∵∠1=40°,∠2=140°,
∴AB与CD不平行;
故本选项错误;
B、如图2:∵∠1=40°,∠2=40°,
∴∠1=∠2,
∴AB与CD平行;
故本选项正确;
C、如图3:∵∠1=40°,∠2=140°,
∴∠1≠∠2,
∴AB不平行CD;
故本选项错误;
D、如图4:∠1=40°,∠2=40°,
∴∠3=140°,
∴∠1≠∠3,
∴AB与CD不平行;
故本选项错误.
故选:B.
3.解:延长ED交AG于点H,
∵AG∥EF,
∴∠E=∠CHD,
∴∠CHD=∠CDE﹣∠DCG,
∵∠B﹣∠DCG=115°,∠B﹣∠CDE=10°,
∴∠CDE=∠B﹣10°,∠DCG=∠B﹣115°,
∴∠E=∠CHD=∠B﹣10°﹣(∠B﹣115°)=105°,
故答案为:105.
4.解:∵DE∥AF,
∴∠2=∠A,
∵∠1=∠2,
∴∠1=∠2=∠A,
∵∠DCF=∠A+∠1=2∠A=100°,
∴∠A=50°,
故答案为:50°.
5.解:过P1作P1G∥AB,可得P1G∥CD,如图,
∴∠BEP1=∠EP1G,∠GP1F=∠P1FD,
∵EP1、FP1分别为∠BEF与∠EFD的平分线,
∴∠BEP1=∠FEP1,∠EFP1=∠DFP1,
∵AB∥CD,
∴∠BEP1+∠FEP1+∠EFP1+∠DFP1=180°,即2(∠BEP1+∠DFP1)=180°,
∴∠BEP1+∠DFP1=90°,
∵∠BEP1、∠DFP1的平分线相交于点K1,
∴∠BEP2=∠P1EP2,∠P1FP2=∠DFP2,
∵∠BEP1+∠FEP1+∠EFP1+∠DFP1=180°,即2(∠BEP1+∠P1FD)=180°,
∴∠BEP1+∠P1FD=90°,即∠P1EP2+∠P1FP2=45°,
∴∠K1=180°﹣(∠P1EF+∠EFP1)﹣(∠P1EP2+∠P1FP2)=45°,
故答案为:45°.
6.解;(1)直线EF与GH的位置关系是平行,理由如下:
如图1,过点C作CD∥EF,
∴∠CAE=∠ACD,
∵∠ACB=∠ACD+∠BCD=80°,∠CAE+∠CBG=80°.
∴∠BCD=∠CBG,
∴CD∥GH,
∴EF∥GH;
(2)∠APB的大小不会随着点B的运动而发生变化,理由如下:
如图2,∵∠CAP=2∠CAE,∠CBP=2∠CBG,
∴∠CAP+∠CBP=2∠CAE+2∠CBG=2(∠CAE+∠CBG)=2×80°=160°,
∴∠APB=360°﹣∠ACB﹣(∠CAP+∠CBP)=360°﹣80°﹣160°=120°.
所以∠APB的大小为120°.
7.解:(1)∵CB∥OA,
∴∠AOC=180°﹣∠C=180°﹣100°=80°,
∵OE平分∠COF,
∴∠COE=∠EOF,
∵∠FOB=∠AOB,
∴∠EOB=∠EOF+∠FOB=∠AOC=×80°=40°;
(2)∵CB∥OA,
∴∠AOB=∠OBC,
∵∠FOB=∠AOB,
∴∠FOB=∠OBC,
∴∠OFC=∠FOB+∠OBC=2∠OBC,
∴∠OBC:∠OFC=1:2,是定值;
(3)在△COE和△AOB中,
∵∠OEC=∠OBA,∠C=∠OAB,
∴∠COE=∠AOB,
∴OB、OE、OF是∠AOC的四等分线,
∴∠COE=∠AOC=×80°=20°,
∴∠OEC=180°﹣∠C﹣∠COE=180°﹣100°﹣20°=60°,
故存在某种情况,使∠OEC=∠OBA,此时∠OEC=∠OBA=60°.
8.解:(1)?明同学辅助线的做法为:过点P作PQ∥AB;
(2)如图2,
∵AB∥PQ∥CD,
∴∠1=∠3,∠4=∠2,
∵∠3+∠4=90°,
∴∠1+∠2=90°,
∵∠1=60°,
∴∠2=90°﹣60°=30°,
如图3,
∵AB∥CD,PF∥EQ,
∴∠2=∠3,∠4=∠3,
∵∠1+∠4=90°,
∴∠1+∠2=90°,
∵∠1=60°,
∴∠2=90°﹣60°=30°,
如图4,
∵AB∥CD,PE∥FQ,
∴∠1=∠3,∠4=∠3,
∵∠2+∠4=90°,
∴∠1+∠2=90°,
∵∠1=60°,
∴∠2=90°﹣60°=30°;
(3)设∠CFE=x,∠PEF=∠PDF=y,
过点P作PQ∥AB,
∴∠BEP+∠EPQ=180°,∠CFE=∠FEB=x,
∵AB∥CD,
∴PQ∥CD,
∴∠PDF=∠DPQ,
∴∠DPQ=∠PEF=∠PDF=y,
由∠CFE=∠FEB=x=∠FEP+∠BEP,
∴x=y+(180°﹣α+y),
∴x﹣2y=180°﹣α,
即∠CFE﹣2∠PEF=180°﹣α.
故答案为:(1)过点P作PQ∥AC;(2)30.
9.解:(1)结论:∠BED+∠D=120°,
证明:如图①,延长AB交DE于点F,
∵AB∥CD,
∴∠BFE=∠D,
∵∠ABE=120°,
∴∠BFE+∠BED=∠ABE=120°,
∴∠D+∠BED=120°;
(2)如图②,
∵∠DEF=2∠BEF,∠CDF=∠CDE,
即∠CDE=3∠CDF,
设∠BEF=α,∠CDF=β,
∴∠DEF=2α,∠DEB=3α,∠CDE=3β,∠EDF=2β,
由(1)知:∠BED+∠CDE=120°,
∴3α+3β=120°,
∴α+β=40°,
∴2α+2β=80°,
∴∠EFD=180°﹣∠DEF﹣∠EDF=180°﹣(2α+2β)=180°﹣80°=100°,
答:∠EFD的度数为100°;
(3)如图③,
∵BG⊥AB,
∴∠ABG=90°,
∵∠ABE=120°.
∴∠GBE=∠ABE﹣∠ABG=30°,
∵∠CDE=4∠GDE,
∴∠GDE=∠CDE,
∵∠G+∠GBE=∠E+∠GDE,
∴∠G+30°=∠E+∠CDE,
由(1)知:∠BED+∠CDE=120°,
∴∠CDE=120°﹣∠E,
∴∠G+30°=∠E+(120°﹣∠E),
∴∠G=∠E,
∴=.
10.证明:(1)如图1,过点P作PG∥AB,
,
∵AB∥CD,
∴PG∥CD,
∴∠AEP=∠1,∠CFP=∠2,
又∵∠1+∠2=∠EPF,
∴∠AEP+∠CFP=∠EPF;
(2)如图2,
,
由(1)可得:∠EPF=∠AEP+CFP,∠EQF=∠BEQ+∠DFQ,
∵∠BEP的平分线与∠DFP的平分线相交于点Q,
∴∠EQF=∠BEQ+∠DFQ=(∠BEP+∠DFP)=[360°﹣(∠AEP+∠CFP)]=(360﹣∠EPF),
∴∠EPF+2∠EQF=360°;
(3)由(1)可得:
∠EGF=∠AEG+∠CFG,∠EPF=∠BEP+∠DFP,
∵∠BEP=∠BEG,∠DFP=∠DFG,
∴∠EPF=∠BEP+∠DFP=(∠BEG+∠DFG)=[360°﹣(∠AEG+∠CFG)]=×(360°﹣∠EGF),
∴∠EGF+n∠EPF=360°.
11.解:(1)∠C=∠1+∠2,
证明:过C作l∥MN,如下图所示,
∵l∥MN,
∴∠4=∠2(两直线平行,内错角相等),
∵l∥MN,PQ∥MN,
∴l∥PQ,
∴∠3=∠1(两直线平行,内错角相等),
∴∠3+∠4=∠1+∠2,
∴∠C=∠1+∠2;
(2)
∵∠BDF=∠GDF,
∵∠BDF=∠PDC,
∴∠GDF=∠PDC,
∵∠PDC+∠CDG+∠GDF=180°,
∴∠CDG+2∠PDC=180°,
∴∠PDC=90°﹣∠CDG,
由(1)可得,∠PDC+∠CEM=∠C=90°,
∴∠AEN=∠CEM,
∴=;
(3)
∵BC平分∠PBD,AM平分∠CAD,∠PBC=25°,
∴∠PBD=2∠PBC=50°,∠CAM=∠MAD,
∵PQ∥MN,
∴∠BMA=∠PBD=50°,
∴∠ADB=∠AMB﹣∠MAD=50°﹣∠MAD=50°﹣∠CAM,
由(1)可得,∠ACB=∠PBC+∠CAM,
∴∠ACB+∠ADB=∠PBC+∠CAM+50°﹣∠CAM=25°+50°=75°.
12.证明:∵AB∥GH(已知),
∴∠1=∠3(两直线平行,内错角相等),
又∵CD∥GH(已知),
∴∠4=∠2(两直线平行,内错角相等).
∵AB∥CD(已知),
∴∠BEF+∠EFD=180°(两直线平行,同旁内角互补).
∵EG平分∠BEF(已知),
∴∠1=∠BEF(角平分线定义),
又∵FG平分∠EFD(已知),
∴∠2=∠EFD(角平分线定义),
∴∠1+∠2=(∠BEF+∠EFD),
∴∠1+∠2=90°,
∴∠3+∠4=90°(等量代换),
即∠EGF=90°.
故答案为:两直线平行,内错角相等;∠4=∠2;∠EFD;∠BEF;角平分线定义;角平分线定义;∠BEF;等量代换.
13.解:(1)∠BEC=∠1+∠3.
证明:过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠BEF=∠1,∠CEF=∠3,
∴∠BEC=∠BEF+∠CEF=∠1+∠3;
(2)∠2+∠4=∠1+∠3+∠5.
理由:分别过点E,G,M,作EF∥AB,GH∥AB,MN∥AB,
∵AB∥CD,
∴AB∥CD∥EF∥GH∥MN,
∴∠1=∠BEF,∠FEG=∠EGH,∠HGM=∠GMN,∠CMN=∠5,
∴∠2+∠4=∠BEF+∠FEG+∠GMN+∠CMN=∠1+∠EGH+∠MGH+∠5=∠1+∠3+∠5;
(3)∠2+∠4+∠6=∠1+∠3+∠5+∠7.
理由:分别过点E,G,M,K,P,作EF∥AB,GH∥AB,MN∥AB,KL∥AB,PQ∥AB,
∵AB∥CD,
∴AB∥CD∥EF∥GH∥MN∥KL∥PQ,
∴∠1=∠BEF,∠FEG=∠EGH,∠HGM=∠GMN,∠KMN=∠LKM,∠LKP=∠KPQ,∠QPC=∠7,
∴∠2+∠4+∠6=∠1+∠3+∠5+∠7.
14.解:(1)如图1,过点M作ML∥AB,
∵AB∥CD,
∴ML∥AB∥CD,
∴∠1=∠AEM,∠2=∠CFM,
∵∠EMF=∠1+∠2,
∴∠M=∠AEM+∠CFM.
故答案为:∠M=∠AEM+∠CFM;
(2)如图2,过M作ME'∥AB,
∵AB∥CD,
∴ME'∥CD,
∴∠BEM+∠2=∠DFM+∠4=180°,
∴∠BEM=180°﹣∠2,∠DFM=180°﹣∠4,
∵EN,FN分别平分∠MEB和∠DFM,
∴∠1=∠BEM,∠3=∠DFM,
∴∠1+∠3=(180°﹣∠2)+(180°﹣∠4)=180°﹣×(∠2+∠4)=180°﹣×130°=115°,
∴∠ENF=360°﹣∠1﹣∠3﹣∠E'MF=360°﹣115°﹣130°=115°;
(3)如图3中设∠BEH=x,∠PFG=y,则∠BEM=3x,∠MFG=3y,设EH交CD于K.
∵AB∥CD,
∴∠BEH=∠DKH=x,
∵∠PFG=∠HFK=y,∠DKH=∠H+∠HFK,
∴∠H=x﹣y,
∵∠EMF=α=∠AEM+∠MFG,
∴∠EMF=180°﹣3x+3y=α
∴x﹣y=60°﹣α,
∴∠H=60°﹣α.
15.解:(1)如图1,过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠ABE=∠BEF,∠CDE=∠DEF,
∵BE平分∠ABC,DE平分∠ADC,∠ADC=70°,
∴∠ABC=2∠ABE=2∠BEF,,
∵∠BED=n°,
∴∠BEF=(n﹣35)°,
∴∠ABC=2∠BEF=2(n﹣35)°=(2n﹣70)°;
(2)∠ABC的度数改变,
画出的图形如图2,过点E作EF∥AB,
∵BE平分∠ABC,DE平分∠ADC,∠ADC=70°,
∴∠ABC=2∠ABE,,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠ABE+∠BEF=180°,∠CDE=∠DEF=35°,
∵∠BED=n°,
∴∠BEF=(n﹣35)°,
∴∠ABE=180°﹣∠BEF=180°﹣(n﹣35)°=180°﹣n°+35°=(215﹣n)°,
∴∠ABC=2∠ABE=2(215﹣n)°=(430﹣2n)°.
16.解:(1)如图(1),过K作KG∥AB,交EF于G,
∵AB∥CD,
∴KG∥CD,
∴∠BEK=∠EKG,∠GKF=∠KFD,
∵EK、FK分别为∠BEF与∠EFD的平分线,
∴∠BEK=∠FEK,∠EFK=∠DFK,
∵AB∥CD,
∴∠BEK+∠FEK+∠EFK+∠DFK=180°,即2(∠BEK+∠DFK)=180°,
∴∠BEK+∠DFK=90°,
则∠EKF=∠EKG+∠GKF=90°;
(2)∠K=2∠K1,理由为:
∵∠BEK、∠DFK的平分线相交于点K1,
∴∠BEK1=∠KEK1,∠KFK1=∠DFK1,
∵∠BEK+∠FEK+∠EFK+∠DFK=180°,即2(∠BEK+∠KFD)=180°,
∴∠BEK+∠KFD=90°,即∠BEK1+∠DFK1=45°,
同理得∠K1=∠BEK1+∠DFK1=45°,
则∠K=2∠K1;
(3)如图(3),
根据(2)中的规律可得:∠K2=∠K1=22.5°,∠K3=∠K2=11.25°,∠K4=∠K3=5.625°.
17.解:∵∠B=∠D=90°,
∴∠DAB+∠BCD=180°,
∵EA∥CF,
∴∠3=∠1,
∵∠3+∠4=90°,
∴∠1+∠4=90°,
∴∠2+∠5=90°,
∵AE平分∠BAD交CD于点E,
∴∠4=∠6,
∴∠4=∠5,
∴∠1=∠2,
∴CF平分∠BCD.
18.解:(1)过E作EF∥AB,
∵AB∥CD,
∴EF∥CD,
∵∠B=15°,
∴∠BEF=15°,
又∵∠BED=90°,
∴∠DEF=75°,
∵EF∥CD,
∴∠D=75°,
故答案为:75°;
(2)过E作EF∥AB,
∵AB∥CD,
∴EF∥CD,
∴∠B+∠BEF+∠DEF+∠D=360°,
又∵∠B=α,∠D=β,
∴∠BED=∠BEF+∠DEF=360°﹣α﹣β,
故答案为:∠BED=360°﹣α﹣β;
(3)猜想:∠BEC=180°﹣α+β.
证明:过点E作EF∥AB,
则∠BEF=180°﹣∠B=180°﹣α,
∵AB∥EF,AB∥CD,
∴EF∥CD,
∴∠CEF=∠C=β,
∴∠BEC=∠BEF+∠CEF=180°﹣α+β.
19.解:(1)过P作PM∥AB,过Q作QN∥AB,
∵AB∥CD,
∴AB∥CD∥PM,AB∥CD∥QN,
∴∠BEP=∠MPE,∠DFP=∠MPF,∠BEQ=∠NQE,∠DFQ=∠FQN,
∴∠BEP+∠DFP=∠MPE+∠MPF=∠EPF=110°,∠BEQ+∠DFQ=∠NQE+∠NQF=∠EQF,
∵QE,QF分别平分∠PEB和∠PFD,
∴∠BEQ+∠DFQ=(∠BEP+∠DFP)=;
猜想:∠EPF与∠EQF的数量关系为∠EPF=2∠EQF.理由如下:
∵AB∥CD,
∴AB∥CD∥PM,AB∥CD∥QN,
∴∠BEP=∠MPE,∠DFP=∠MPF,∠BEQ=∠NQE,∠DFQ=∠FQN,
∴∠BEP+∠DFP=∠MPE+∠MPF=∠EPF,∠BEQ+∠DFQ=∠NQE+∠NQF=∠EQF,
∵QE,QF分别平分∠PEB和∠PFD,
∴2(∠BEQ+∠DFQ)=∠BEP+∠DFP=∠EPF,
即∠EPF=2∠EQF;
故答案为55°;
(2)2∠EQF+∠EPF=360°.理由如下:
如图2,过P作PM∥AB,过Q作QN∥AB,
∵AB∥CD,
∴AB∥CD∥PM,AB∥CD∥QN,
∴∠BEP+∠MPE=180°,∠DFP+∠MPF=180°,∠BEQ=∠NQE,∠DFQ=∠FQN,
∴∠BEP+∠DFP+∠MPE+∠MPF=360°即∠BEP+∠DFP+∠EPF=360°,∠EQF∠BEQ+∠DFQ=∠NQE+∠NQF=∠EQF,
∵QE,QF分别平分∠PEB和∠PFD,
∴∠BEQ+∠DFQ=(∠BEP+∠DFP)=∠EQF,即∠BEP+∠DFP=2∠EQF,
∴2∠EQF+∠EPF=360°;
(3)当点P在EF的左侧,
根据(1)的方法可得∠Q1=(∠BEP+∠DFP)=∠EQF,
∠Q2=(∠BEP+∠DFP)=∠EQF,
…
则∠Qn=()n(∠BEP+∠DFP)=()n∠EQF,
∵2∠EQF+∠EPF=360°,∠BEP+∠DFP=2∠EQF,
∴∠EPF+2n+1?∠EQnF=360°.
当点P在EF的右侧,同理可求∠EPF=2n+1∠EQnF.
20.解:①∵AB∥CD,∠α=50°
∴∠2=∠α=50°,
故答案为50;
(2)∠α=∠1+∠2.
证明:过P作PG∥AB,
∵AB∥CD,
∴PG∥AB∥CD,
∴∠2=∠EPG,∠1=∠FPG,
∵∠α=∠EPF=∠EPG+∠FPG,
∴∠α=∠1+∠2;
(3)不成立.
理由:过P作PH∥AB,
∵AB∥CD,
∴PH∥AB∥CD,
∴∠2=∠EPH,∠1=∠FPH,
∵∠α=∠EPF=∠EPH﹣∠FPH,
∴∠α=∠2﹣∠1,
故不成立.
21.(1)证明:如图1,过点P作PG∥AB,
,
∵AB∥CD,
∴PG∥CD,
∴∠AEP=∠1,∠CFP=∠2,
又∵∠1+∠2=∠EPF,
∴∠AEP+∠CFP=∠EPF;
(2)如图2,
,
由(1)可得:∠EPF=∠AEP+CFP,∠EQF=∠BEQ+∠DFQ,
∵∠BEP的平分线与∠DFP的平分线相交于点Q,
∴∠EQF=∠BEQ+∠DFQ=(∠BEP+∠DFP)=[360°﹣(∠AEP+∠CFP)]=(360﹣∠EPF),
∴∠EPF+2∠EQF=360°;
(3)由(1)可得:∠P=∠AEP+CFP,∠Q=∠BEQ+∠DFQ,
∵∠BEQ=∠BEP,∠DFQ=∠DFP,
∴∠Q=∠BEQ+∠DFQ=(∠BEP+∠DFP)=[360°﹣(∠AEP+∠CFP)]=×(360°﹣∠P),
∴∠P+n∠Q=360°;
故答案为:∠P+n∠Q=360°.
22.解:(1)如图1,过点G作GH∥AB,
∵AB∥CD,
∴GH∥AB∥CD,
∴∠AMG=∠HGM,∠CNG=∠HGN,
∵GM⊥GN,
∴∠MGN=∠MGH+∠HGN=∠AMG+∠CNG=90°;
答:∠AMG+∠CNG的度数为90°;
(2)如图2,过过点G作GK∥AB,过点P作PQ∥AB,设∠GND=α,
∵GK∥AB,AB∥CD,
∴GK∥CD,
∴∠KGN=∠GND=α,
∵GK∥AB,∠BMG=40°,
∴∠MGK=∠BMG=40°,
∵MG平分∠BMP,
∴∠GMP=∠BMG=40°,
∴∠BMP=80°,
∵ND平分∠GNP,
∴∠DNP=∠GND=α,
∵AB∥CD,
∴PQ∥CD,
∴∠QPN=∠DNP=α,
∴∠MGN=40°+α,∠MPN=80°﹣α,
∴∠MGN+∠MPN=40°+α+80°﹣α=120°.
23.解:(1)作PE∥AB,
∵AB∥CD,AB∥PE,
∴CD∥PE,
∴∠APE=∠A,∠CPE=∠DCP,
∴∠APC=∠APE+∠CPE=∠BAP+∠DCP.
故答案为∠APC=∠BAP+∠DCP.
(2)①作图如图1:
设∠DCP=β,
由(1)可得,∠APC=α+β,
∵AK平分∠BAP,
∴∠BAK=∠BAP=α,
同理,∠LCD=(180°﹣β)=90°﹣β,
过点Q作QM∥AB,如图2,则∠MQK=∠BAK=,
∵AB∥CD,
∴QM∥CD,
∴,
∴;
②∵AP∥QC,
∴∠AQC=∠KAP,
由①得,∠AQC=90°﹣(α+β),
∴,
整理得,β=180°﹣2β,即∠DCP=180°﹣2β.
24.解:(1)∠1=∠2,
理由:如图1,
∵AB∥EF,
∴∠3=∠2,
∵BC∥DE,
∴∠3=∠1,
∴∠1=∠2;
(2)∠1+∠2=180°,
理由:如图2,
∵AB∥EF,
∴∠3+∠2=180°,
∵BC∥DE,
∴∠3=∠1,
∴∠1+∠2=180°.
(3)如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.
故答案为:一个角的两边与另一个角的两边分别平行,这两个角相等或互补;
(4)设另一个角为x°,根据以上结论得:
2x﹣60=x或2x﹣60+x=180,
解得:x=60,或x=80,
故答案为:60°、60°或80°,100°.
25.解:(1)如图1中,过点E作EG∥AB,
则∠BEG=∠ABE,
因为AB∥CD,EG∥AB,
所以CD∥EG,
所以∠DEG=∠CDE,
所以∠BEG+∠DEG=∠ABE+∠CDE,
即∠BED=∠ABE+∠CDE;
(2)图2中,因为BF平分∠ABE,
所以∠ABE=2∠ABF,
因为DF平分∠CDE,
所以∠CDE=2∠CDF,
所以∠ABE+∠CDE=2∠ABF+2∠CDF=2(∠ABF+∠CDF),
由(1)得:因为AB∥CD,
所以∠BED=∠ABE+∠CDE,
∠BFD=∠ABF+∠CDF,
所以∠BED=2∠BFD.
(3)∠BED=360°﹣2∠BFD.
图3中,过点E作EG∥AB,
则∠BEG+∠ABE=180°,
因为AB∥CD,EG∥AB,
所以CD∥EG,
所以∠DEG+∠CDE=180°,
所以∠BEG+∠DEG=360°﹣(∠ABE+∠CDE),
即∠BED=360°﹣(∠ABE+∠CDE),
因为BF平分∠ABE,
所以∠ABE=2∠ABF,
因为DF平分∠CDE,
所以∠CDE=2∠CDF,
∠BED=360°﹣2(∠ABF+∠CDF),
由(1)得:因为AB∥CD,
所以∠BFD=∠ABF+∠CDF,
所以∠BED=360°﹣2∠BFD.
26.证明:∵∠ABC+∠ECB=180°(已知),
∴AB∥DE(同旁内角互补,两直线平行).
∴∠ABC=∠BCD(两直线平行,内错角相等).
∵∠P=∠Q(已知),
∴PB∥(CQ)(内错角相等,两直线平行).
∴∠PBC=(∠BCQ)(两直线平行,内错角相等).
∵∠1=∠ABC﹣(∠PBC),∠2=∠BCD﹣(∠BCQ),
∴∠1=∠2(等量代换).
故答案为:同旁内角互补,两直线平行;两直线平行,内错角相等;CQ,内错角相等,两直线平行;∠BCQ;∠PBC;∠BCQ.
27.(1)证明:∵AC∥BD,
∴∠DAE=∠BDA,
∵∠BDA=∠C,
∴∠DAE=∠C,
∴AD∥BC;
(2)证明:如图2,设CE与BD相交于点G,∠BGA=∠BDA+DAE,
∵BD⊥BC,
∴∠BGA+∠C=90°,
∴∠BDA+∠DAE+∠C=90°,
∵∠BDA=∠C,
∴∠DAE+2∠C=90°;
(3)如图3,设∠DAE=α,则∠DFE=8α,
∵∠DFE+∠AFD=180°,
∴∠AFD=180°﹣8α,
∵DF∥BC,
∴∠C=∠AFD=180°﹣8α,
又∵2∠C+∠DAE=90°,
∴2(180°﹣8α)+α=90°,
∴α=18°,
∴∠C=180°﹣8α=36°=∠ADB,
又∵∠C=∠BDA,∠BAC=∠BAD,
∴∠ABC=∠ABD=∠CBD=45°,
△ABD中,∠BAD=180°﹣45°﹣36°=99°.
答:∠BAD的度数是99°.
28.证明:∵AD∥BC,
∴∠2=∠E,
∵AE平分∠BAD,
∴∠1=∠2,
∴∠1=∠E,
∵∠CFE=∠E,
∴∠1=∠CFE,
∴AB∥DC.
29.解:(1)①由条件可知:∠1与∠3的大小关系是相等,理由是两直线平行,同位角相等;∠2与∠4的大小关系是相等;
②反射光线BC与EF的位置关系是平行,理由是同位角相等,两直线平行;
故答案为:①相等、两直线平行,同位角相等、相等;②平行、同位角相等,两直线平行.
(2)如图,
∵∠1=40°,
∴∠4=∠1=40°,
∴∠6=180°﹣40°﹣40°=100°,
∵m∥n,
∴∠2+∠6=180°,
∴∠2=80°,
∴∠5=∠7==50°,
∴∠3=180°﹣50°﹣40°=90°.
30.证明:∵AB∥CD,
∴∠1=∠ACD,
∵∠1=∠2,
∴∠2=∠ACD,
∴∠2+∠CAE=∠ACD+∠CAE,
∴∠DAC=∠4,
∵∠3=∠4,
∴∠DAC=∠3,
∴AD∥BE.
31.解:(1)∠PEQ=∠APE+∠CQE,理由如下:
∵AB∥CD,EH∥AB,
∴AB∥EH∥CD,
∴∠APE=∠PEH,∠CQE=∠QEH.
∵∠PEQ=∠PEH+∠QEH,
∴∠PEQ=∠APE+∠CQE.
(2)∠APE+∠CQE+∠PEQ=360°;理由如下:
过点E作EG∥AB,如图2所示:
∵AB∥CD,EG∥AB,
∴AB∥EG∥CD,
∴∠APE+∠PEG=180°,∠CQE+∠QEG=180°,
∴∠APE+∠PEG+∠CQE+∠QEG=360°,
即∠APE+∠CQE+∠PEQ=360°;
(3)由(2)得:∠PEQ+∠BPE+∠EQD=360°,
∵∠PEQ=140°,
∴∠BPE+∠EQD=360°﹣140°=220°,
∵PF平分∠BPE,QF平分∠EQD,
∴∠BPF=∠BPE,∠DQF=∠EQD,
∴∠BPF+∠DQF=(∠BPE+∠EQD)=110°,
由(1)得:∠PFQ=∠BPF+∠DQF=110°.
32.解:AB∥CD.
理由如下:作BE⊥NB,CF⊥NC,如图,
∵∠1=∠2,∠3=∠4,BE∥NC,
∴∠2=∠NCB,
∴∠2+∠3=∠1+∠4=90°,
∴∠ABC+∠BCD=180°,
∴AB∥CD.
33.解:(1)过点E、F分别作EM∥AB,FN∥AB,如图2所示:
∵EM∥AB,
∴∠1=∠B,
又∵FN∥AB,
∴FN∥EM,
∴∠2=∠3,
又∵AB∥CD,
∴FN∥CD,
∴∠4+∠C=180°,
又∵∠BEF=∠1+∠2,∠EFC=∠3+∠4,∠BEF=60°
∴∠B+∠EFC+∠C=∠1+∠3+∠4+∠C
=(∠1+∠2)+(∠4+∠C)
=60°+180°
=240°;
(2)过点G、H作EF∥AB,MN∥AB,如图3所示:
∵BE平分∠ABG,CF平分∠DCG,
∴∠ABG=2∠1,∠DCG=2∠4,
又∵EF∥AB,
∴2∠1+∠7=180°,
又∵AB∥CD,
∴EF∥CD,
∴2∠4+∠8=180°,
∴∠7+∠8=360°﹣2(∠1+∠4),
又∵∠7+∠8+∠BGC=180°,
∴2(∠1+∠4)=∠BGC+180°,
又∵MN∥AB,
∴∠1=∠5,
又∵AB∥CD,
∴MN∥CD,
∴∠4=∠6,
∴2(∠5+∠6)=∠BGC+180°,
又∵∠5+∠6+∠BHC=180°,
∴∠BGC+2∠BHC=180°,
又∠BGC=∠BHC+27°,
∴3∠BHC+27°=180°,
∴∠BHC=51°;
故答案为:240°,51°.
34.解:(1)∵AM∥BN,
∴∠MAB+∠2=180°,
∵∠MAB+∠1+∠BAC=180°,∠1=∠BAC,∠1=35°,
∴∠2=2∠1=70°,
∵∠2+∠ABC+∠NBF=180°,∠ABC=∠NBF,
∴∠ABC=55°,
∴∠3=180°﹣∠BAC﹣∠ABC=90°;
当∠1=50°时,
同理可得,∠2=100°,∠ABC=40°,∠BAC=∠1=50°,
则∠3=180°﹣∠BAC﹣∠ABC=90°;
故答案为:70°,90°,90°;
(2)猜想:当两平面镜CE,CF的夹角∠3为90°时,可以使任何射到平面镜CE上的光线MA,经过平面镜CE,CF的两次反射后,入射光线MA与反射光线BN平行.
理由:∵∠3=90°,
∴∠BAC+∠ABC=90°,
∵∠1=∠BAC,∠ABC=∠NBF,
∴∠BAC+∠1+∠ABC+∠NBF=180°,
∴∠MAB+∠2=180°,
∴MA∥BN.
35.解:感知与填空:过点E作直线EF∥CD,
∴∠2=∠D(两直线平行,内错角相等),
∵AB∥CD(已知),EF∥CD,
∴AB∥EF(两直线都和第三条直线平行,那么这两条直线也互相平行),
∴∠B=∠1(两直线平行,内错角相等),
∵∠1+∠2=∠BED,
∴∠B+∠D=∠BED(等量代换),
故答案为:两直线平行,内错角相等;两直线都和第三条直线平行,那么这两条直线也互相平行;两直线平行,内错角相等;等量代换.
应用与拓展:过点G作GN∥AB,
则GN∥CD,如图②所示:
由感知与填空得:∠E=∠B+∠EGN,∠F=∠D+∠FGN,
∴∠E+∠F=∠B+∠EGN+∠D+∠FGN=∠B+∠D+∠EGF=22°+25°+35°=82°,
故答案为:82.
方法与实践:设AB交EF于M,如图③所示:
∠AME=∠FMB=180°﹣∠F﹣∠B=180°﹣80°﹣60°=40°,
由感知与填空得:∠E=∠D+∠AME,
∴∠D=∠E﹣∠AME=60°﹣40°=20°,
故答案为:20.
36.解:(1)过点P作EF∥AB,
∴∠B+∠BPE=180°,
∵AB∥CD,EF∥AB,
∴CD∥EF(如果两条直线都和第三条直线平行,那么这两条直线也互相平行),
∴∠EPD+∠D=180°,
∴∠B+∠BPE+∠EPD+∠D=360°,
∴∠B+∠BPD+∠D=360°,
故答案为:CD∥EF,∠D;
(2)猜想∠BPD=∠B+∠D,
理由:过点P作EP∥AB,
∵EP∥AB,
∴∠B=∠BPE(两直线平行,内错角相等),
∵AB∥CD,EP∥AB,
∴CD∥EP(如果两条直线都和第三条直线平行,那么这两条直线也互相平行),
∴∠EPD=∠D,
∴∠BPD=∠B+∠D;
(3)图③结论:∠D=∠BPD+∠B,
理由是:过点P作EP∥AB,
∵EP∥AB,
∴∠B=∠BPE(两直线平行,内错角相等),
∵AB∥CD,EP∥AB,
∴CD∥EP(如果两条直线都和第三条直线平行,那么这两条直线也互相平行),
∴∠EPD=∠D,
∴∠D=∠BPD+∠B;
图④结论∠B=∠BPD+∠D,
理由是:∵EP∥AB,
∴∠B=∠BPE(两直线平行,内错角相等),
∵AB∥CD,EP∥AB,
∴CD∥EP(如果两条直线都和第三条直线平行,那么这两条直线也互相平行),
∴∠EPD=∠D,
∴∠B=∠BPD+∠D.
37.证明:∵∠1=∠2
(已知)
又∵∠1=∠3
(对顶角相等
)
∴∠2=∠3
(等量代换)
∴CE∥FDB(
同位角相等,两直线平行
)
∴∠B=∠CEA
(两直线平行,同位角相等
)
∵∠B=∠C
(已知)
∴∠C=∠CEA
(等量代换)
∴AB∥CD
(内错角相等,两直线平行
)
∴∠A=∠D.(
两直线平行,内错角相等
)
38.解:BF与AC的位置关系是:BF⊥AC.
理由:∵∠AGF=∠ABC,
∴BC∥GF,
∴∠1=∠3;
又∵∠1+∠2=180°,
∴∠2+∠3=180°,
∴BF∥DE;
∵DE⊥AC,
∴BF⊥AC.
39.证明:∵∠3=∠4,
∴CF∥BD,
∴∠5=∠FAB;
∵∠5=∠6,
∴∠6=∠FAB,
∴AB∥CD,
∴∠2=∠EGA;
∵∠1=∠2,
∴∠1=∠EGA,
∴ED∥FB
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
