2020-2021学年高一数学人教A版必修二第三章3.1.1 倾斜角与斜率课件(共18张PPT)
文档属性
| 名称 | 2020-2021学年高一数学人教A版必修二第三章3.1.1 倾斜角与斜率课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-12 00:00:00 | ||
图片预览


文档简介
(共18张PPT)
3.1.1直线的
倾斜角和斜率
问题1:生活中也有一些反映倾斜程度的量,
你知道有哪些量可以用来表示某一斜坡的倾
斜程度吗?
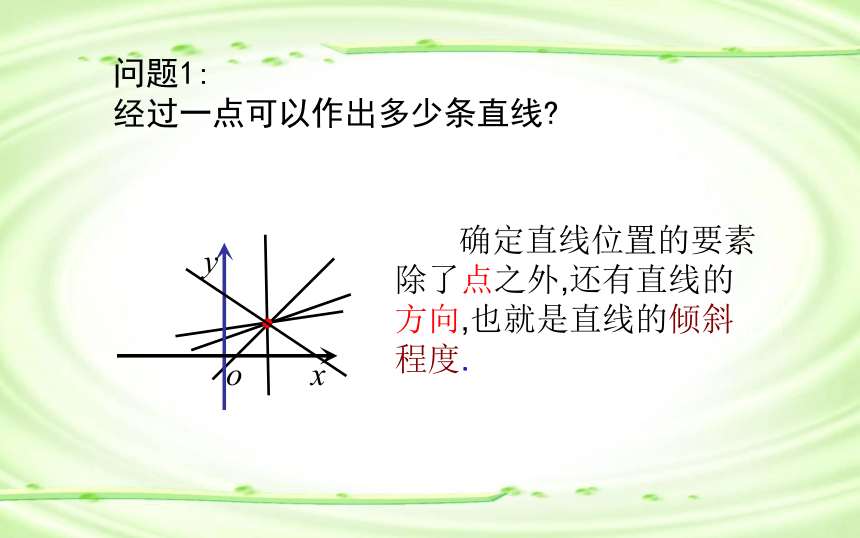
类似的,能否引进一个来刻画直
线的倾斜程度的量?
进
建构概念:1直线的倾斜角
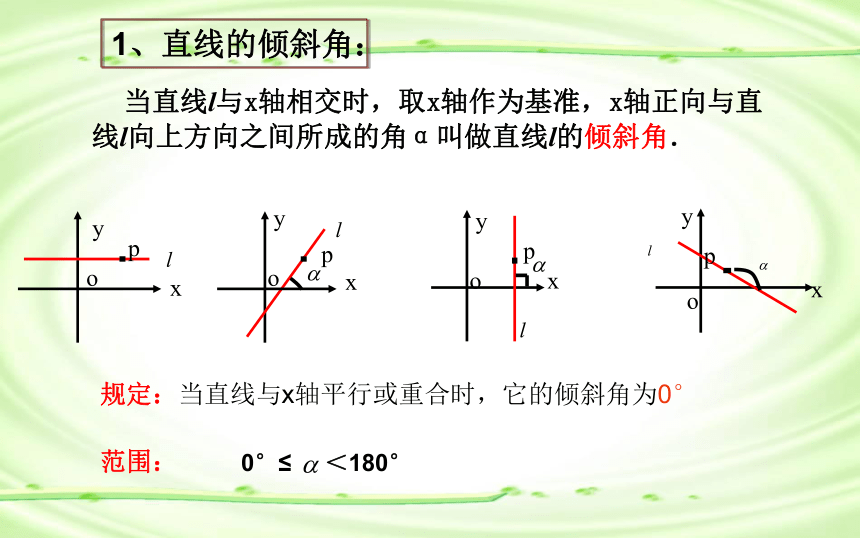
当直线L与x轴相交时,我们取x轴作为基准
x轴正向与直线向上方向之间所成的a角叫做
直线的倾斜角。
规定:当直线和x轴平行或重合时,它的倾斜角为0
直线的倾斜角的取值范围为:0°≤a<180°
定义:
我们把一条直线的倾斜角α的正切值叫做
这条直线的斜率.常用小写字母k表示,即
k=
tan
a
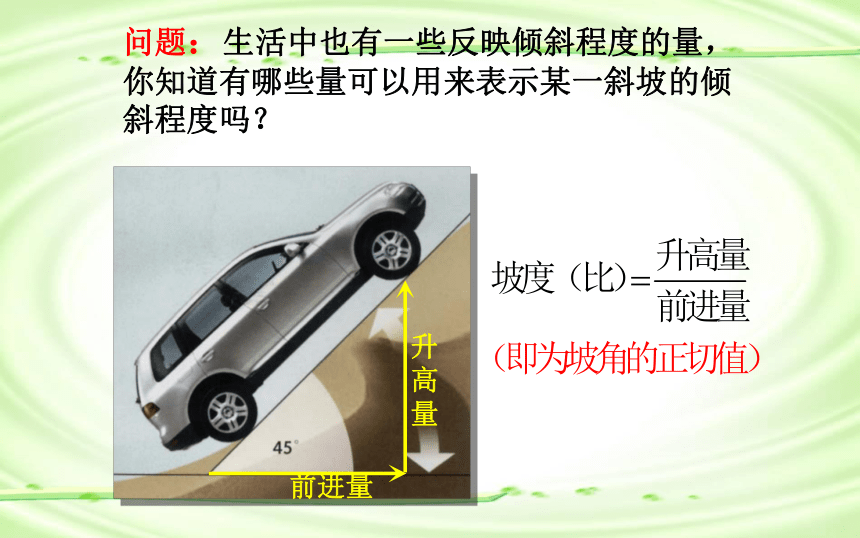
问题2::生活中也有一些反映倾斜程度的量,
你知道有哪些量可以用来表示某一斜坡的倾斜
程度吗?
坡度(比)升高量
前进量
腐、(即为坡角的正切值)
一前进
a
n
O
moyo(
o
po
k=tano(≠90°)
课前检测题:已知下列直线的倾斜角,求直线的斜率
(1)a=30;(2)a=45;
(3)a=120
(4)a=135;
解:(1)k=tan30=-
(2)k=tan45=1
(3)k=tan120=-√3
(4)k=tan135=-1
命
04
45
倾斜角3060135150
(度)
斜率33-133
例2(《新概念》变式2)
若经过点P(1-a,1+a)和Q(3,2a)的
直线的倾斜角为钝角,求实数a的取值范围
解:∵直线PQ的倾斜角为钝角,
且k<0
+2
<0
a+2
解得:-2管线斜率的定义
定义:一条直线倾斜角的正切叫做这条直线的斜率。
斜率通常用k表示,即
tana
例如:a=0°→k=tan0=0
a=30°→k=tan30√3
a=45°→k=tan45=1
a=60°→k=tan60
两点的斜率公式了
当a为钝角时,a=180-∠QP2,x1>x2
JI
tana=
tan(180-0)=-tanB
在直角△PPQ中
tane_lOP=2H
V23-y
I
PQI
r-xz
.I
tana
x,-x
y个
x2,n2)
2(2,y1)
R(,y1)
O
两点的斜率公式
k=
tana=
y2-y1
思考
t-x
当直线P2P与x轴平行或重合时,上述式子还
成立吗?为什么
成立
经过两点P(x1,y)P(x2,y2X(x1≠x2)的直线的
斜率公式为:
k=yav
O
两点的斜率公式了
k=tana=少2二儿
思考
2.当直线平行于y轴,或与y轴重合时,上述斜
率公式还适用吗?为什么?
x2万)
P,(
x·ya
适用
3.1.1直线的
倾斜角和斜率
问题1:生活中也有一些反映倾斜程度的量,
你知道有哪些量可以用来表示某一斜坡的倾
斜程度吗?
类似的,能否引进一个来刻画直
线的倾斜程度的量?
进
建构概念:1直线的倾斜角
当直线L与x轴相交时,我们取x轴作为基准
x轴正向与直线向上方向之间所成的a角叫做
直线的倾斜角。
规定:当直线和x轴平行或重合时,它的倾斜角为0
直线的倾斜角的取值范围为:0°≤a<180°
定义:
我们把一条直线的倾斜角α的正切值叫做
这条直线的斜率.常用小写字母k表示,即
k=
tan
a
问题2::生活中也有一些反映倾斜程度的量,
你知道有哪些量可以用来表示某一斜坡的倾斜
程度吗?
坡度(比)升高量
前进量
腐、(即为坡角的正切值)
一前进
a
n
O
moyo(
o
po
k=tano(≠90°)
课前检测题:已知下列直线的倾斜角,求直线的斜率
(1)a=30;(2)a=45;
(3)a=120
(4)a=135;
解:(1)k=tan30=-
(2)k=tan45=1
(3)k=tan120=-√3
(4)k=tan135=-1
命
04
45
倾斜角3060135150
(度)
斜率33-133
例2(《新概念》变式2)
若经过点P(1-a,1+a)和Q(3,2a)的
直线的倾斜角为钝角,求实数a的取值范围
解:∵直线PQ的倾斜角为钝角,
且k<0
+2
<0
a+2
解得:-2
定义:一条直线倾斜角的正切叫做这条直线的斜率。
斜率通常用k表示,即
tana
例如:a=0°→k=tan0=0
a=30°→k=tan30√3
a=45°→k=tan45=1
a=60°→k=tan60
两点的斜率公式了
当a为钝角时,a=180-∠QP2,x1>x2
JI
tan(180-0)=-tanB
在直角△PPQ中
tane_lOP=2H
V23-y
I
PQI
r-xz
.I
tana
x,-x
y个
x2,n2)
2(2,y1)
R(,y1)
O
两点的斜率公式
k=
tana=
y2-y1
思考
t-x
当直线P2P与x轴平行或重合时,上述式子还
成立吗?为什么
成立
经过两点P(x1,y)P(x2,y2X(x1≠x2)的直线的
斜率公式为:
k=yav
O
两点的斜率公式了
k=tana=少2二儿
思考
2.当直线平行于y轴,或与y轴重合时,上述斜
率公式还适用吗?为什么?
x2万)
P,(
x·ya
适用
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
