椭圆的简单几何性质
图片预览







文档简介
(共30张PPT)
复习:
1.椭圆的定义:
到两定点F1、F2的距离之和为常数(大于|F1F2 |)的动点的轨迹叫做椭圆。
2.椭圆的标准方程是:
3.椭圆中a,b,c的关系是:
a2=b2+c2
当焦点在X轴上时
当焦点在Y轴上时
2.1.2《 椭圆的几何性质》
椭圆的几何性质
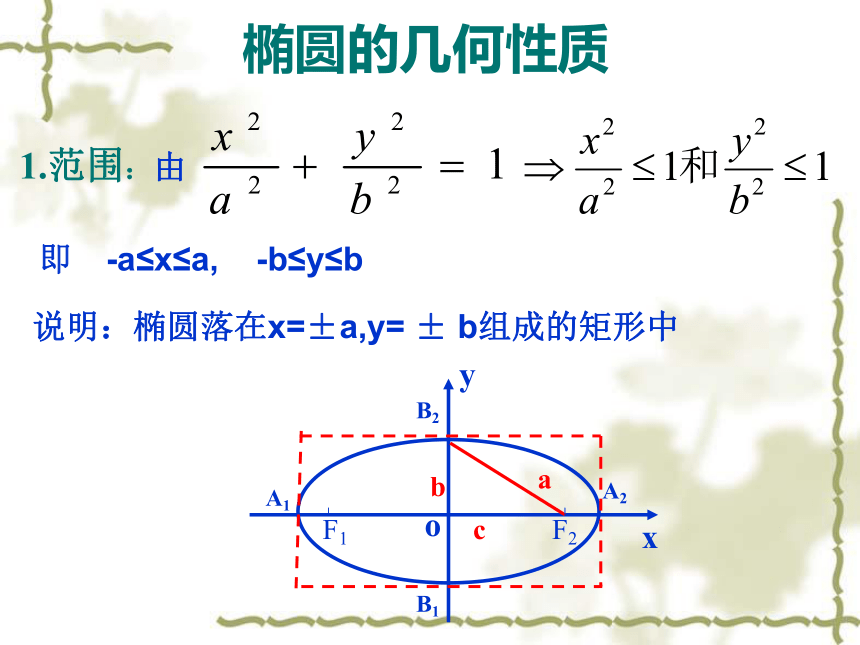
1.范围:由
即 -a≤x≤a, -b≤y≤b
说明:椭圆落在x=±a,y= ± b组成的矩形中
o
y
B2
B1
A1
A2
F1
F2
c
a
b
x
1.范 围:
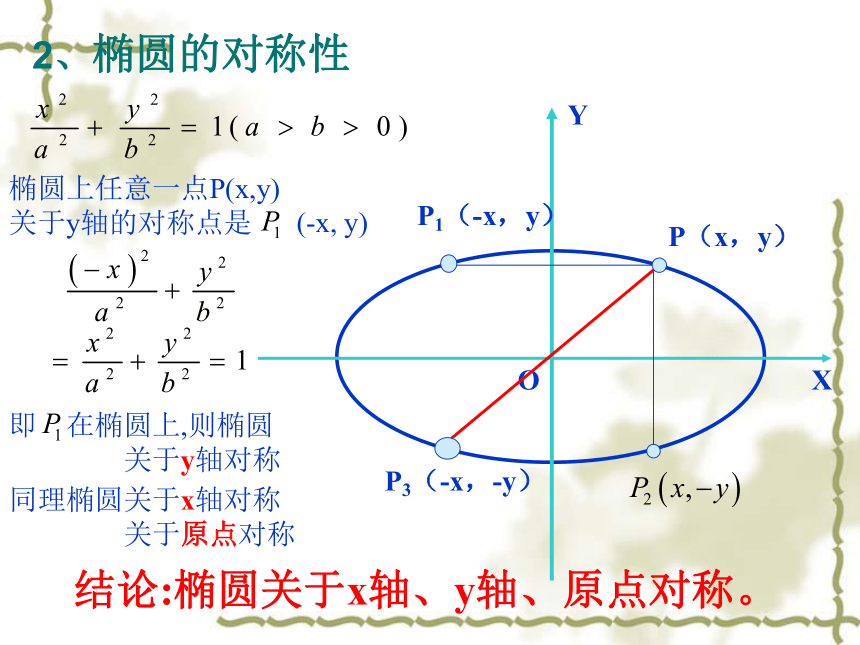
2、椭圆的对称性
Y
X
O
P(x,y)
P1(-x,y)
P3(-x,-y)
结论:椭圆关于x轴、y轴、原点对称。
椭圆上任意一点P(x,y)
关于y轴的对称点是
同理椭圆关于x轴对称
关于原点对称
即 在椭圆上,则椭圆
关于y轴对称
(-x, y)
F2
F1
O
x
y
椭圆关于y轴对称。
F2
F1
O
x
y
椭圆关于x轴对称。
A2
A1
A2
F2
F1
O
x
y
椭圆关于原点对称。
3、椭圆的顶点
令 x=0,得 y=?,说明椭圆与 y轴的交点?
令 y=0,得 x=?说明椭圆与 x轴的交点?
*顶点:椭圆与它的对称轴的四个交点,叫做椭圆的顶点。
*长轴、短轴:线段A1A2、B1B2分别叫做椭圆的长轴和短轴。
a、b分别叫做椭圆的长半轴长和短半轴长。
o
y
B2
B1
A1
A2
F1
F2
c
a
b
(0,b)
(a,0)
(0,-b)
(-a,0)
学生活动(课本41页练习1)
思考:已知椭圆的长轴A1A2和短轴B1B2 ,怎样确定椭圆焦点的位置?
o
B2
B1
A1
A2
F1
F2
a
a
c
c
b
因为a2=b2+c2,所以以椭圆短轴端点为圆心,a长为半径的圆与x轴的交点即为椭圆焦点.
4、离心率
长半轴为 a
半焦距为 c
思考:保持长半轴 a 不变,改变椭圆的半焦距 c ,我们可以发现,c 越接近 a ,椭圆越________
这样,我们就可以利用__和__这两个量来刻画椭圆的扁平程度
扁平
c
a
看动画
椭圆的离心率
因为 a >c>0,所以 e 的取值范围是:_________
0e 越接近于1,则c越接近于a,从而b就越小,因此椭圆就越扁反之,e越接近于0, c 就越接近于0,从而b 就越接近于 a,这时椭圆就越接近于圆
当且仅当a=b时,c=0,这时两个焦点就_____,图形变为 ___,它的方程为:
重合
圆
看动画
4、椭圆的离心率
e与a,b的关系:
课本41页 练习 5(1)
标准方程
范围
对称性
顶点坐标
焦点坐标
半轴长
离心率
a、b、c的关系
|x|≤ a,|y|≤ b
关于x 轴、y 轴成轴对称;关于原点成中心对称
(a,0)、(-a,0)、(0,b)、(0,-b)
(c,0)、(-c,0)
长半轴长为a,短半轴长为b. a>b
a2=b2+c2
标准方程
范围
对称性
顶点坐标
焦点坐标
半轴长
离心率
a、b、c的关系
|x|≤ a,|y|≤ b
关于x 轴、y 轴成轴对称;关于原点成中心对称
(a,0)、(-a,0)、(0,b)、(0,-b)
(c,0)、(-c,0)
长半轴长为a,短半轴长为b. a>b
a2=b2+c2
|x|≤ b,|y|≤ a
同前
(b,0)、(-b,0)、(0,a)、(0,-a)
(0 , c)、(0, -c)
同前
同前
同前
例4
求椭圆 16 x2 + 25y2 =400的长轴和短轴的长、离心率、焦点和顶点坐标
解:把已知方程化成标准方程
这里,
因此,椭圆的长轴长和短轴长分别是
离心率
焦点坐标分别是
四个顶点坐标是
解题的关键:1、将椭圆方程转化为标准方程
2、确定焦点的位置和长轴的位置
例.求适合下列条件的椭圆的标准方程:
(1)经过点P(-3,0),Q(0,-2);
(2)长轴长等于20,离心率等于 .
解:
(1)由椭圆的几何性质可知,点P、Q分别为椭圆长轴和短轴的一个端点.
为所求椭圆的标准方程 .
课本41页 练习 3
解:
x
y
.
.
F
F ’
O
.
M
.
例6.点M(x,y)与定点F(c,0)的距离和它到定直线 的距离的比是常数 ,求点M的轨迹
椭圆第二定义:
x
y
.
.
F
F ’
O
.
M
复习:
1.椭圆的定义:
到两定点F1、F2的距离之和为常数(大于|F1F2 |)的动点的轨迹叫做椭圆。
2.椭圆的标准方程是:
3.椭圆中a,b,c的关系是:
a2=b2+c2
当焦点在X轴上时
当焦点在Y轴上时
2.1.2《 椭圆的几何性质》
椭圆的几何性质
1.范围:由
即 -a≤x≤a, -b≤y≤b
说明:椭圆落在x=±a,y= ± b组成的矩形中
o
y
B2
B1
A1
A2
F1
F2
c
a
b
x
1.范 围:
2、椭圆的对称性
Y
X
O
P(x,y)
P1(-x,y)
P3(-x,-y)
结论:椭圆关于x轴、y轴、原点对称。
椭圆上任意一点P(x,y)
关于y轴的对称点是
同理椭圆关于x轴对称
关于原点对称
即 在椭圆上,则椭圆
关于y轴对称
(-x, y)
F2
F1
O
x
y
椭圆关于y轴对称。
F2
F1
O
x
y
椭圆关于x轴对称。
A2
A1
A2
F2
F1
O
x
y
椭圆关于原点对称。
3、椭圆的顶点
令 x=0,得 y=?,说明椭圆与 y轴的交点?
令 y=0,得 x=?说明椭圆与 x轴的交点?
*顶点:椭圆与它的对称轴的四个交点,叫做椭圆的顶点。
*长轴、短轴:线段A1A2、B1B2分别叫做椭圆的长轴和短轴。
a、b分别叫做椭圆的长半轴长和短半轴长。
o
y
B2
B1
A1
A2
F1
F2
c
a
b
(0,b)
(a,0)
(0,-b)
(-a,0)
学生活动(课本41页练习1)
思考:已知椭圆的长轴A1A2和短轴B1B2 ,怎样确定椭圆焦点的位置?
o
B2
B1
A1
A2
F1
F2
a
a
c
c
b
因为a2=b2+c2,所以以椭圆短轴端点为圆心,a长为半径的圆与x轴的交点即为椭圆焦点.
4、离心率
长半轴为 a
半焦距为 c
思考:保持长半轴 a 不变,改变椭圆的半焦距 c ,我们可以发现,c 越接近 a ,椭圆越________
这样,我们就可以利用__和__这两个量来刻画椭圆的扁平程度
扁平
c
a
看动画
椭圆的离心率
因为 a >c>0,所以 e 的取值范围是:_________
0
当且仅当a=b时,c=0,这时两个焦点就_____,图形变为 ___,它的方程为:
重合
圆
看动画
4、椭圆的离心率
e与a,b的关系:
课本41页 练习 5(1)
标准方程
范围
对称性
顶点坐标
焦点坐标
半轴长
离心率
a、b、c的关系
|x|≤ a,|y|≤ b
关于x 轴、y 轴成轴对称;关于原点成中心对称
(a,0)、(-a,0)、(0,b)、(0,-b)
(c,0)、(-c,0)
长半轴长为a,短半轴长为b. a>b
a2=b2+c2
标准方程
范围
对称性
顶点坐标
焦点坐标
半轴长
离心率
a、b、c的关系
|x|≤ a,|y|≤ b
关于x 轴、y 轴成轴对称;关于原点成中心对称
(a,0)、(-a,0)、(0,b)、(0,-b)
(c,0)、(-c,0)
长半轴长为a,短半轴长为b. a>b
a2=b2+c2
|x|≤ b,|y|≤ a
同前
(b,0)、(-b,0)、(0,a)、(0,-a)
(0 , c)、(0, -c)
同前
同前
同前
例4
求椭圆 16 x2 + 25y2 =400的长轴和短轴的长、离心率、焦点和顶点坐标
解:把已知方程化成标准方程
这里,
因此,椭圆的长轴长和短轴长分别是
离心率
焦点坐标分别是
四个顶点坐标是
解题的关键:1、将椭圆方程转化为标准方程
2、确定焦点的位置和长轴的位置
例.求适合下列条件的椭圆的标准方程:
(1)经过点P(-3,0),Q(0,-2);
(2)长轴长等于20,离心率等于 .
解:
(1)由椭圆的几何性质可知,点P、Q分别为椭圆长轴和短轴的一个端点.
为所求椭圆的标准方程 .
课本41页 练习 3
解:
x
y
.
.
F
F ’
O
.
M
.
例6.点M(x,y)与定点F(c,0)的距离和它到定直线 的距离的比是常数 ,求点M的轨迹
椭圆第二定义:
x
y
.
.
F
F ’
O
.
M
