2020--2021学年人教版八年级下册 16.3 :二次根式的加减 (1)课件(17张)
文档属性
| 名称 | 2020--2021学年人教版八年级下册 16.3 :二次根式的加减 (1)课件(17张) |  | |
| 格式 | ppt | ||
| 文件大小 | 299.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-11 00:19:24 | ||
图片预览





文档简介
16.3 二次根式的加减(1)
二次根式计算、化简的结果符合什么要求?
(1)被开方数不含分母;
(2)被开方数中不含能开得尽 方的因数
或因式.
最简二次根式
1、观察下列二次根式有什么共同特征:
(1) ……
, , ,
(2) ……
, , ,
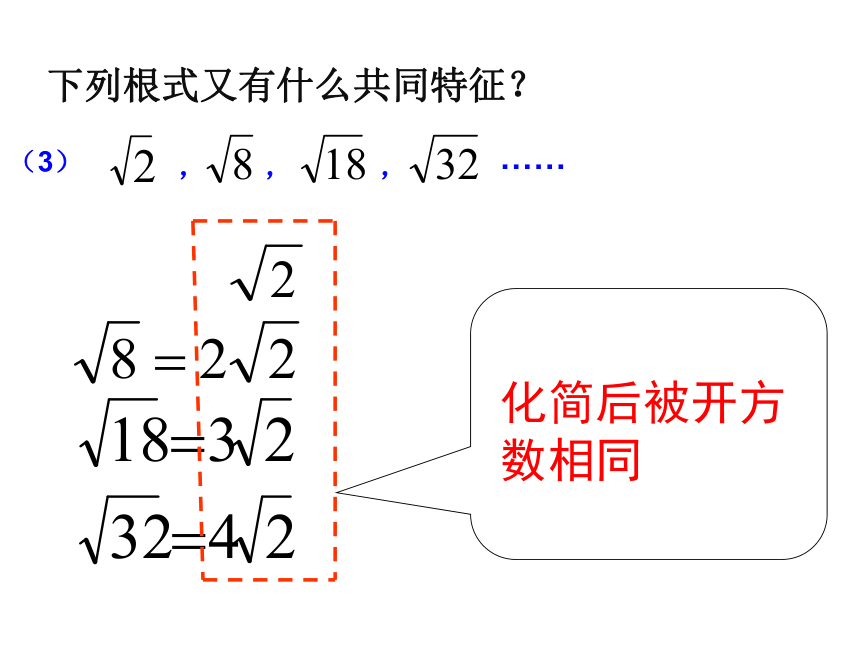
(3)
……
, , ,
化简后被开方数相同
下列根式又有什么共同特征?
几个二次根式化成最简二次根式以后,如果被开方数相同,这几个二次根式就叫做同类二次根式.
判断同类二次根式的关键是什么?
(1)化成最简二次根式;
(2)被开方数相同,根指数相同(都等于2).
归纳总结
练一练
1.下列各式中,与 是同类二次根式的是( )
A. B. C. D.
D
2. 与最简二次根式 能合并,则m=_____.
1
3.下列二次根式,不能与 合并的是________(填
序号).
②⑤
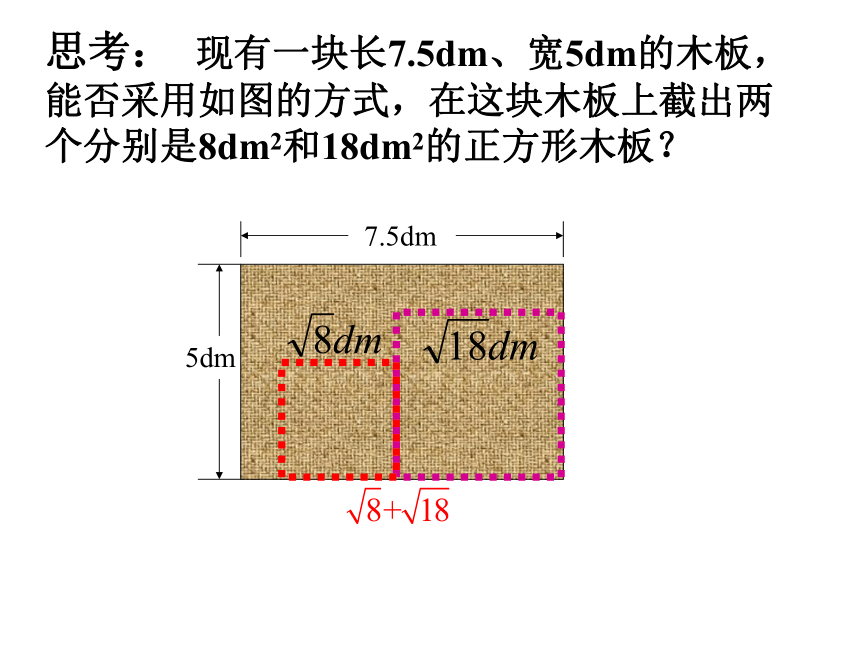
思考: 现有一块长7.5dm、宽5dm的木板,能否采用如图的方式,在这块木板上截出两个分别是8dm2和18dm2的正方形木板?
7.5dm
5dm
所列算式能直接进行加减运算吗?如果不能,把式中各个二次根式化成最简二次根式后,再试一试(说出每步运算的依据).
(化成最简二次根式)
(逆用分配律)
∴在这块木板上可以截出两个分别是8dm2和18dm2的正方形木板.
解:列式如下:
在有理数范围内成立的运算律,在实数范围内仍然成立.
比较二次根式的加减与整式的加减,你能得出什么结论?
先化简,后合并
二次根式加减法的法则是什么?
(1)化——将非最简二次根式的二次根式化简;
加减法的运算步骤:
(2)找——找出被开方数相同的二次根式;
(3)并——把被开方数相同的二次根式合并.
“一化简二判断三合并”
例2 计算:
解:
例3 计算:
解:
有括号,先去括号
例4 已知a,b,c满足 .
(1)求a,b,c的值;
(2)以a,b,c为三边长能否构成三角形?若能构成
三角形,求出其周长;若不能,请说明理由.
解:(1)由题意得 ;
(2)能.理由如下:∵ 即a<c<b,
又∵ ∴a+c>b,
∴能构成三角形,周长为
分析:(1)若几个非负数的和为零,则这几个非负数必须为零;(2)根据三角形的三边关系来判断.
课堂小结
1、判断同类二次根式的关键是什么?
(1)化成最简二次根式,
(2)被开方数相同,根指数相同(都等于2)
2、二次根式加减运算的步骤:
(3)合并同类二次根式。
(1)将每个二次根式化为最简二次根式;
(2)找出其中的同类二次根式;
“一化简二判断三合并”
1.二次根式: 中,与 能进行合并的
是 ( )
A.
B .
C .
D .
2.下列运算中错误的是 ( )
A.
B.
C.
D.
A
C
3.三角形的三边长分别为 则这个三角形的周长为__________.
4.计算:
解:
5.计算:
解:
二次根式计算、化简的结果符合什么要求?
(1)被开方数不含分母;
(2)被开方数中不含能开得尽 方的因数
或因式.
最简二次根式
1、观察下列二次根式有什么共同特征:
(1) ……
, , ,
(2) ……
, , ,
(3)
……
, , ,
化简后被开方数相同
下列根式又有什么共同特征?
几个二次根式化成最简二次根式以后,如果被开方数相同,这几个二次根式就叫做同类二次根式.
判断同类二次根式的关键是什么?
(1)化成最简二次根式;
(2)被开方数相同,根指数相同(都等于2).
归纳总结
练一练
1.下列各式中,与 是同类二次根式的是( )
A. B. C. D.
D
2. 与最简二次根式 能合并,则m=_____.
1
3.下列二次根式,不能与 合并的是________(填
序号).
②⑤
思考: 现有一块长7.5dm、宽5dm的木板,能否采用如图的方式,在这块木板上截出两个分别是8dm2和18dm2的正方形木板?
7.5dm
5dm
所列算式能直接进行加减运算吗?如果不能,把式中各个二次根式化成最简二次根式后,再试一试(说出每步运算的依据).
(化成最简二次根式)
(逆用分配律)
∴在这块木板上可以截出两个分别是8dm2和18dm2的正方形木板.
解:列式如下:
在有理数范围内成立的运算律,在实数范围内仍然成立.
比较二次根式的加减与整式的加减,你能得出什么结论?
先化简,后合并
二次根式加减法的法则是什么?
(1)化——将非最简二次根式的二次根式化简;
加减法的运算步骤:
(2)找——找出被开方数相同的二次根式;
(3)并——把被开方数相同的二次根式合并.
“一化简二判断三合并”
例2 计算:
解:
例3 计算:
解:
有括号,先去括号
例4 已知a,b,c满足 .
(1)求a,b,c的值;
(2)以a,b,c为三边长能否构成三角形?若能构成
三角形,求出其周长;若不能,请说明理由.
解:(1)由题意得 ;
(2)能.理由如下:∵ 即a<c<b,
又∵ ∴a+c>b,
∴能构成三角形,周长为
分析:(1)若几个非负数的和为零,则这几个非负数必须为零;(2)根据三角形的三边关系来判断.
课堂小结
1、判断同类二次根式的关键是什么?
(1)化成最简二次根式,
(2)被开方数相同,根指数相同(都等于2)
2、二次根式加减运算的步骤:
(3)合并同类二次根式。
(1)将每个二次根式化为最简二次根式;
(2)找出其中的同类二次根式;
“一化简二判断三合并”
1.二次根式: 中,与 能进行合并的
是 ( )
A.
B .
C .
D .
2.下列运算中错误的是 ( )
A.
B.
C.
D.
A
C
3.三角形的三边长分别为 则这个三角形的周长为__________.
4.计算:
解:
5.计算:
解:
