2020-2021学年高一上学期数学人教B版(2019)必修第二册第四章4.7数学建模活动(3)-课件(共44张PPT)
文档属性
| 名称 | 2020-2021学年高一上学期数学人教B版(2019)必修第二册第四章4.7数学建模活动(3)-课件(共44张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-11 00:00:00 | ||
图片预览





文档简介
数学建模活动(3)
高一年级 数学
思考:什么是数学建模?数学建模的过程包含哪些步骤?
数学建模:对现实问题进行数学抽象,用数学语言表达问题,用数学方法构建模型解决问题的过程.
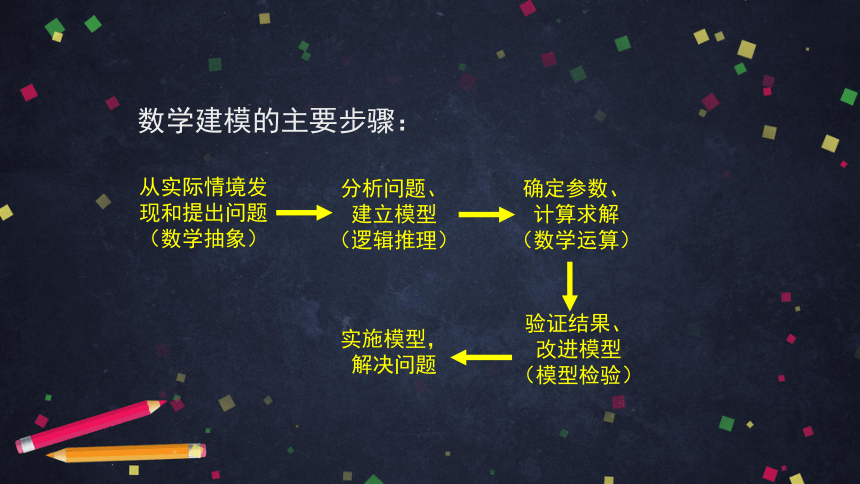
数学建模的主要步骤:
从实际情境发现和提出问题(数学抽象)
分析问题、
建立模型
(逻辑推理)
确定参数、
计算求解
(数学运算)
验证结果、
改进模型
(模型检验)
实施模型,解决问题
在前面的学习中,我们接触到了指数函数、对数函数、幂函数这三类具体函数的定义、性质与图像,比较了这三类函数的增长速度.
有了这些工具,我们可以解决生活中更多的实际问题,这节课我们将借助函数模型来描述自然界中生物的生长规律问题.
生物的生长是一个怎样的变化过程?你能结合你自己的生长发育过程说说你的看法吗?
生物的生长发育是一个连续的过程,但不同的时间段可能有不同的增长速度.
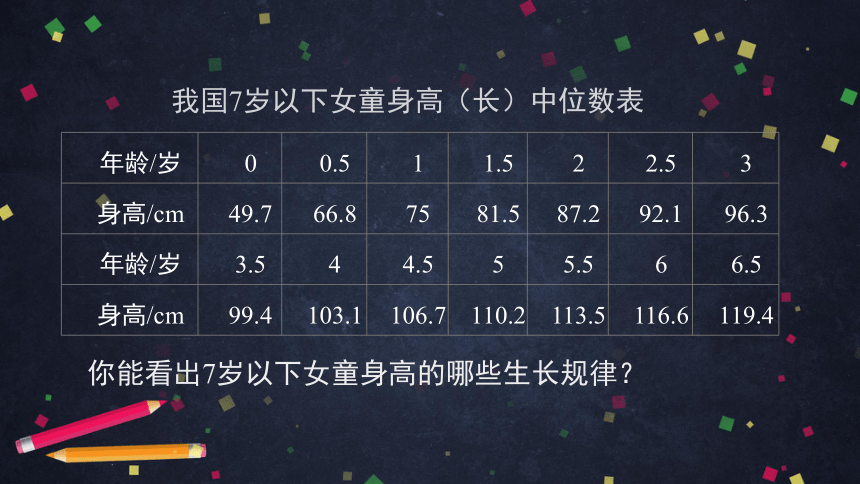
例 卫生部2009年发布的《中国7岁以下儿童生长发育参照标准》指出,我国7岁以下女童身高(长)的中位数如下表所示(0岁指刚出生):
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}年龄/岁
0
0.5
1
1.5
2
2.5
3
身高/cm
49.7
66.8
75
81.5
87.2
92.1
96.3
年龄/岁
3.5
4
4.5
5
5.5
6
6.5
身高/cm
99.4
103.1
106.7
110.2
113.5
116.6
119.4
我国7岁以下女童身高(长)中位数表
你能看出7岁以下女童身高的哪些生长规律?
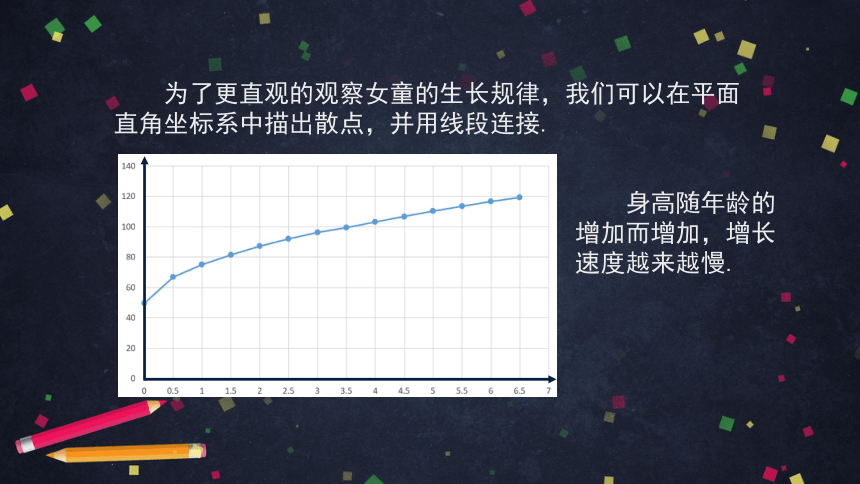
为了更直观的观察女童的生长规律,我们可以在平面直角坐标系中描出散点,并用线段连接.
身高随年龄的增加而增加,增长速度越来越慢.
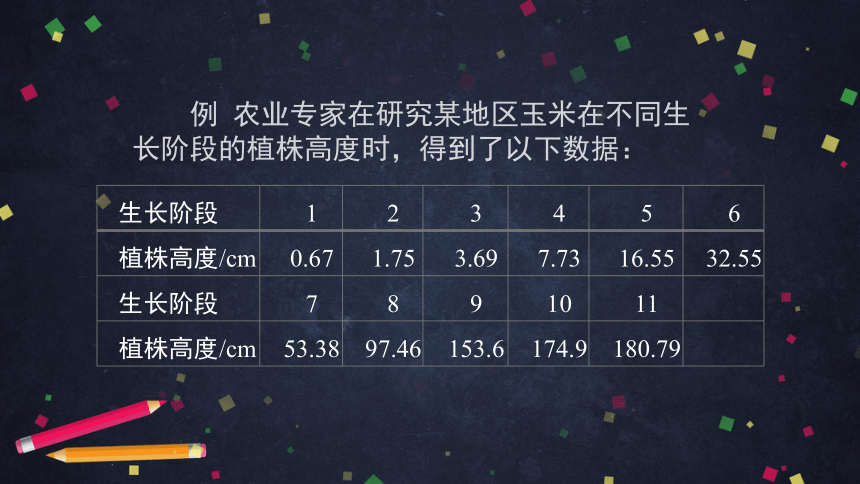
例 农业专家在研究某地区玉米在不同生长阶段的植株高度时,得到了以下数据:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}生长阶段
1
2
3
4
5
6
植株高度/cm
0.67
1.75
3.69
7.73
16.55
32.55
生长阶段
7
8
9
10
11
植株高度/cm
53.38
97.46
153.6
174.9
180.79
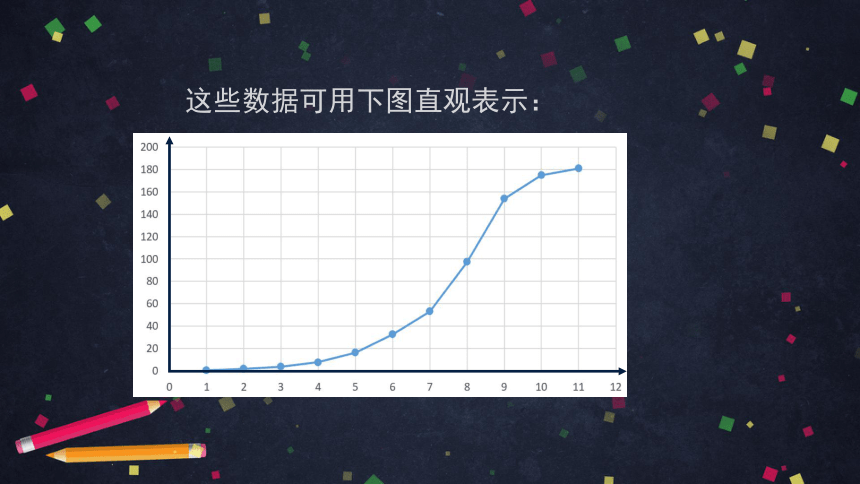
这些数据可用下图直观表示:
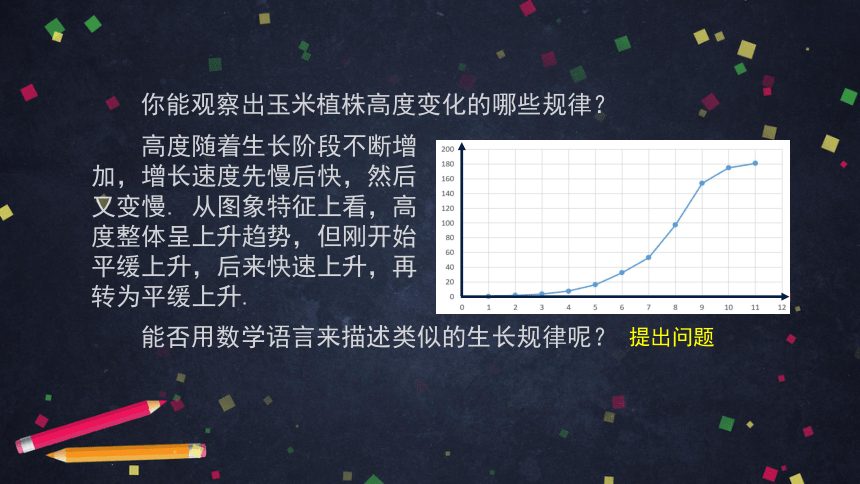
高度随着生长阶段不断增加,增长速度先慢后快,然后又变慢. 从图象特征上看,高度整体呈上升趋势,但刚开始平缓上升,后来快速上升,再转为平缓上升.
你能观察出玉米植株高度变化的哪些规律?
能否用数学语言来描述类似的生长规律呢?
提出问题
上面两个例子中的生长规律都是一个量(女童身高或植株高度,记为 )随着另一个量(生长阶段,记为 )的变化而变化,且符合函数的定义,因此,我们可以借助函数
来描述生长规律.
根据实际情况,可以假设变量 都是连续变化的,从上面两个例子的图象的特征可以看出 应具有什么性质?
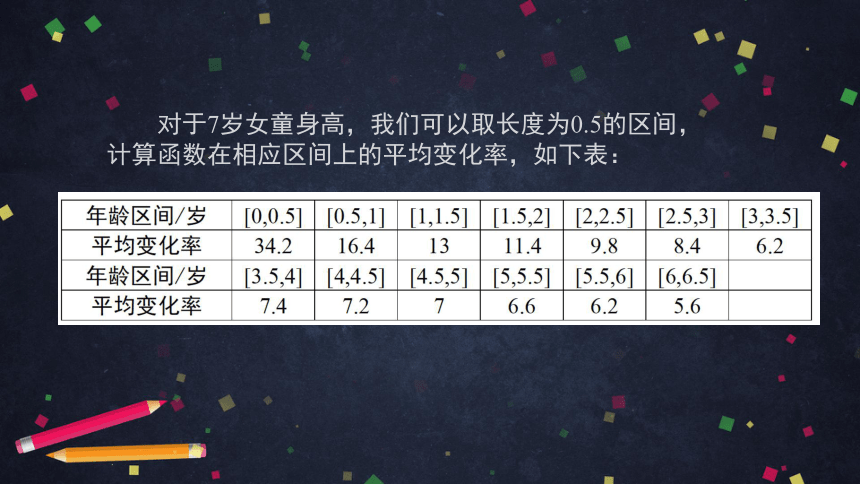
对于7岁女童身高,我们可以取长度为0.5的区间,计算函数在相应区间上的平均变化率,如下表:
从上表可以看出女童身高对应的函数在相应区间上的平均变化率都是正数,说明这应该是一个增函数,但增长速度不是大致不变的,而是越来越慢.
同样的,我们也可以计算出植株高度在相应区间上的平均变化率,如下表:
可以发现增长速度也不是大致不变的,它呈现了先慢后快,再变慢的趋势.
因此,我们可以认为生长函数 在指定的范围内是增函数,但不同的时间段对应不同增长速度,所以不会是一次函数.
选择什么函数类型来描述不同对象的生长规律?
女童身高的变化趋势(刚开始增长较快,后来慢慢变缓)与我们学习过的幂函数 的图象相似,可以考虑用函数
来描述.
建立模型
提出问题
玉米植株高度的增长速度刚开始较慢,后来逐渐加快,可以联系我们学习过的指数函数 ,尝试用函数
来描述.
建立模型
提出问题
参数求解
建立模型
提出问题
若选择 ,则有
需通过两组数据建立两个方程进行求解.
对于函数 ,如何求参数
的值?
解得
所以
参数求解
建立模型
提出问题
类似的,对于函数 ,也可以选择两组数据对参数进行求解.
若选择 ,可解得
所以
参数求解
建立模型
提出问题
模型检验
由于在进行参数求解时,只用到了部分数据,我们需要利用其他数据来检验所建立的模型的优劣. 你能提供一个判断模型优劣的方法吗?
我们建立的模型能否符合实际情况?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}年龄/岁
0
0.5
1
1.5
2
2.5
3
身高/cm
49.7
66.8
75
81.5
87.2
92.1
96.3
49.7
68.6
76.4
82.4
87.5
91.9
95.9
年龄/岁
3.5
4
4.5
5
5.5
6
6.5
身高/cm
99.4
103.1
106.7
110.2
113.5
116.6
119.4
99.7
103.1
106.3
109.4
112.3
115.1
117.8
参数求解
建立模型
提出问题
模型检验
对于女童身高生长规律问题,利用
计算对应函数值,可得下表:
参数求解
建立模型
提出问题
模型检验
参数求解
建立模型
提出问题
模型检验
可以看到,误差都在2cm以内,所以可以认为
能较好的反映我国7岁以下女童身高的生长规律.
我们可以利用这个模型进行预估,如7岁女童的
身高的中位数约为
cm.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}生长阶段
1
2
3
4
5
6
植株高度/cm
0.67
1.75
3.69
7.73
16.55
32.55
?
0.90
1.75
3.42
6.68
13.05
25.51
生长阶段
7
8
9
10
11
?
植株高度/cm
53.38
97.46
153.6
174.9
180.79
?
?
49.85
97.46
190.40
372.08
727.14
?
参数求解
建立模型
提出问题
模型检验
对于玉米植株高度生长规律问题,计算
对应的函数值,可得下表:
参数求解
建立模型
提出问题
模型检验
参数求解
建立模型
提出问题
模型检验
参数求解
建立模型
提出问题
模型检验
可以看到,在前8个阶段, 函数值与真实值之间的误差不大,但从第9阶段开始,误差非常大,所以 不能反映出玉米植株高度的实际增长规律.
参数求解
建立模型
提出问题
模型检验
指数函数的增长速度会越来越快,与植株高度增长速度先慢后快,再慢的规律并不一致.
你能分析造成这个结果的原因吗?
我们可以计算植株高度在每个阶段的增长率,如下表:
可以看出,前8个阶段的增长率大致都在1上下波动,但从第9阶段开始迅速减小. 所以前期类似于指数增长,可以用指数模型去刻画,但后期已不符合前期指数增长的特征.
参数求解
建立模型
提出问题
模型检验
事实上,对于玉米及自然界诸多种群来说,在自然界有限资源的环境内种群的生长不可能无限增长,应该会存在一个饱和水平. 当种群增长到接近于饱和水平时,增长速度会逐渐减慢趋近于0,所以玉米植株高度增长应类似于一个S型曲线,而并非呈指数增长.
为什么植株高度不可能一直按指数增长下去呢?你能从现实情境角度给出解释吗?
你能进一步改进这个模型吗?
可以以第9段为界分段描述或者更换函数模型.
若以第9段为界分段描述:
将
代入
,可解得:
所以
此时计算
与真实值
相差不大.
怎样描述总体的误差情况?
能否计算每组函数值与真实值的差,再进行求和?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}生长阶段
1
2
3
4
5
6
植株高度/cm
0.67
1.75
3.69
7.73
16.55
32.55
?
0.90
1.75
3.42
6.68
13.05
25.51
误差
0.23
0
-0.27
-1.05
-3.5
-7.04
生长阶段
7
8
9
10
11
?
植株高度/cm
53.38
97.46
153.6
174.9
180.79
?
?
49.85
97.46
190.40
372.08
727.14
?
误差
-3.53
0
36.8
197.18
546.35
如何避免正负相消?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}生长阶段
1
2
3
4
5
6
植株高度/cm
0.67
1.75
3.69
7.73
16.55
32.55
?
0.90
1.75
3.42
6.68
13.05
25.51
误差
0.23
0
-0.27
-1.05
-3.5
-7.04
生长阶段
7
8
9
10
11
?
植株高度/cm
53.38
97.46
153.6
174.9
180.79
?
?
49.85
97.46
190.40
372.08
727.14
?
误差
-3.53
0
36.8
197.18
546.35
可以计算误差的平方和,来刻画总体的误差情况.
经计算,在h(x)模型下,误差的平方和为338808.
对于
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}生长阶段
1
2
3
4
5
6
植株高度/cm
0.67
1.75
3.69
7.73
16.55
32.55
?
0.90
1.75
3.42
6.68
13.05
25.51
误差
0.23
0
-0.27
-1.05
-3.5
-7.04
生长阶段
7
8
9
10
11
?
植株高度/cm
53.38
97.46
153.6
174.9
180.79
?
?
49.85
97.46
0
-8.34
0
?
误差
-3.53
0
0
69.56
0
经计算,在H(x)模型下,误差的平方和约为145.06.
因此,我们可以通过计算不同模型下误差的平方和来比较模型之间的优劣. 在玉米植株生长规律问题中,
能更好的描述玉米植株高度的变化规律.
也可以考虑更换函数模型. 人们一般用逻辑斯蒂(logistic)模型
来描述类似玉米植株高度的增长规律,这个模型的建立过程需要用到高等数学的知识,大家上大学以后可以对其进行推导. 我们现在可以利用这个模型,选择合适数据,确定其中的三个参数,并将函数值与真实值进行比较,验证模型. 请大家在课后完成.
改进模型
参数求解
建立模型
提出问题
模型检验
我们还可以借助信息技术,如使用数学软件GeoGebra进行函数拟合.
在GeoGebra的表格区中输入玉米植株高度的数据:
点击“双变量回归分析”后,选择“逻辑拟合”:
可以得到利用逻辑斯蒂模型进行函数拟合的结果,同时还可以得到对应函数的解析式:
对于 ,也可以计算相应的误差:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}生长阶段
1
2
3
4
5
6
植株高度/cm
0.67
1.75
3.69
7.73
16.55
32.55
?
0.26
0.68
1.76
4.53
11.41
27.24
误差
-0.41
-1.07
-1.93
-3.20
-5.14
-5.31
生长阶段
7
8
9
10
11
?
植株高度/cm
53.38
97.46
153.6
174.9
180.79
?
?
58.08
102.5
144.88
172.12
185.47
?
误差
4.70
5.04
-8.72
-2.78
4.68
经计算,在F(x)模型下,误差的平方和约为222.98.
抽象、推理和模型是数学的基本思想,学数学最终的目的是应用所学数学知识分析和解决问题.
改进模型
参数求解
建立模型
提出问题
模型检验
实施模型
数学建模活动与之前我们做的文字应用题的区别在于其情境的真实性和条件与问题的开放性. 我们需要了解数学建模的过程与步骤,可以通过数学抽象、数学建模和逻辑推理去解决更多的实际问题.
小结
作业
组建数学建模小组,在以下两个题目中,任选一个进行数学建模实践:
(1)观察特定植物(如葱、水仙花)的生长情况,定期记录有关数据,探索生长规律,并按照类似本节的方法建立对应的生长模型.
(2)了解人口增长规律,查找某一地区或某一国家人口的历史数据,尝试建立相关的数学模型,并利用模型进行预测.
谢谢
高一年级 数学
思考:什么是数学建模?数学建模的过程包含哪些步骤?
数学建模:对现实问题进行数学抽象,用数学语言表达问题,用数学方法构建模型解决问题的过程.
数学建模的主要步骤:
从实际情境发现和提出问题(数学抽象)
分析问题、
建立模型
(逻辑推理)
确定参数、
计算求解
(数学运算)
验证结果、
改进模型
(模型检验)
实施模型,解决问题
在前面的学习中,我们接触到了指数函数、对数函数、幂函数这三类具体函数的定义、性质与图像,比较了这三类函数的增长速度.
有了这些工具,我们可以解决生活中更多的实际问题,这节课我们将借助函数模型来描述自然界中生物的生长规律问题.
生物的生长是一个怎样的变化过程?你能结合你自己的生长发育过程说说你的看法吗?
生物的生长发育是一个连续的过程,但不同的时间段可能有不同的增长速度.
例 卫生部2009年发布的《中国7岁以下儿童生长发育参照标准》指出,我国7岁以下女童身高(长)的中位数如下表所示(0岁指刚出生):
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}年龄/岁
0
0.5
1
1.5
2
2.5
3
身高/cm
49.7
66.8
75
81.5
87.2
92.1
96.3
年龄/岁
3.5
4
4.5
5
5.5
6
6.5
身高/cm
99.4
103.1
106.7
110.2
113.5
116.6
119.4
我国7岁以下女童身高(长)中位数表
你能看出7岁以下女童身高的哪些生长规律?
为了更直观的观察女童的生长规律,我们可以在平面直角坐标系中描出散点,并用线段连接.
身高随年龄的增加而增加,增长速度越来越慢.
例 农业专家在研究某地区玉米在不同生长阶段的植株高度时,得到了以下数据:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}生长阶段
1
2
3
4
5
6
植株高度/cm
0.67
1.75
3.69
7.73
16.55
32.55
生长阶段
7
8
9
10
11
植株高度/cm
53.38
97.46
153.6
174.9
180.79
这些数据可用下图直观表示:
高度随着生长阶段不断增加,增长速度先慢后快,然后又变慢. 从图象特征上看,高度整体呈上升趋势,但刚开始平缓上升,后来快速上升,再转为平缓上升.
你能观察出玉米植株高度变化的哪些规律?
能否用数学语言来描述类似的生长规律呢?
提出问题
上面两个例子中的生长规律都是一个量(女童身高或植株高度,记为 )随着另一个量(生长阶段,记为 )的变化而变化,且符合函数的定义,因此,我们可以借助函数
来描述生长规律.
根据实际情况,可以假设变量 都是连续变化的,从上面两个例子的图象的特征可以看出 应具有什么性质?
对于7岁女童身高,我们可以取长度为0.5的区间,计算函数在相应区间上的平均变化率,如下表:
从上表可以看出女童身高对应的函数在相应区间上的平均变化率都是正数,说明这应该是一个增函数,但增长速度不是大致不变的,而是越来越慢.
同样的,我们也可以计算出植株高度在相应区间上的平均变化率,如下表:
可以发现增长速度也不是大致不变的,它呈现了先慢后快,再变慢的趋势.
因此,我们可以认为生长函数 在指定的范围内是增函数,但不同的时间段对应不同增长速度,所以不会是一次函数.
选择什么函数类型来描述不同对象的生长规律?
女童身高的变化趋势(刚开始增长较快,后来慢慢变缓)与我们学习过的幂函数 的图象相似,可以考虑用函数
来描述.
建立模型
提出问题
玉米植株高度的增长速度刚开始较慢,后来逐渐加快,可以联系我们学习过的指数函数 ,尝试用函数
来描述.
建立模型
提出问题
参数求解
建立模型
提出问题
若选择 ,则有
需通过两组数据建立两个方程进行求解.
对于函数 ,如何求参数
的值?
解得
所以
参数求解
建立模型
提出问题
类似的,对于函数 ,也可以选择两组数据对参数进行求解.
若选择 ,可解得
所以
参数求解
建立模型
提出问题
模型检验
由于在进行参数求解时,只用到了部分数据,我们需要利用其他数据来检验所建立的模型的优劣. 你能提供一个判断模型优劣的方法吗?
我们建立的模型能否符合实际情况?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}年龄/岁
0
0.5
1
1.5
2
2.5
3
身高/cm
49.7
66.8
75
81.5
87.2
92.1
96.3
49.7
68.6
76.4
82.4
87.5
91.9
95.9
年龄/岁
3.5
4
4.5
5
5.5
6
6.5
身高/cm
99.4
103.1
106.7
110.2
113.5
116.6
119.4
99.7
103.1
106.3
109.4
112.3
115.1
117.8
参数求解
建立模型
提出问题
模型检验
对于女童身高生长规律问题,利用
计算对应函数值,可得下表:
参数求解
建立模型
提出问题
模型检验
参数求解
建立模型
提出问题
模型检验
可以看到,误差都在2cm以内,所以可以认为
能较好的反映我国7岁以下女童身高的生长规律.
我们可以利用这个模型进行预估,如7岁女童的
身高的中位数约为
cm.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}生长阶段
1
2
3
4
5
6
植株高度/cm
0.67
1.75
3.69
7.73
16.55
32.55
?
0.90
1.75
3.42
6.68
13.05
25.51
生长阶段
7
8
9
10
11
?
植株高度/cm
53.38
97.46
153.6
174.9
180.79
?
?
49.85
97.46
190.40
372.08
727.14
?
参数求解
建立模型
提出问题
模型检验
对于玉米植株高度生长规律问题,计算
对应的函数值,可得下表:
参数求解
建立模型
提出问题
模型检验
参数求解
建立模型
提出问题
模型检验
参数求解
建立模型
提出问题
模型检验
可以看到,在前8个阶段, 函数值与真实值之间的误差不大,但从第9阶段开始,误差非常大,所以 不能反映出玉米植株高度的实际增长规律.
参数求解
建立模型
提出问题
模型检验
指数函数的增长速度会越来越快,与植株高度增长速度先慢后快,再慢的规律并不一致.
你能分析造成这个结果的原因吗?
我们可以计算植株高度在每个阶段的增长率,如下表:
可以看出,前8个阶段的增长率大致都在1上下波动,但从第9阶段开始迅速减小. 所以前期类似于指数增长,可以用指数模型去刻画,但后期已不符合前期指数增长的特征.
参数求解
建立模型
提出问题
模型检验
事实上,对于玉米及自然界诸多种群来说,在自然界有限资源的环境内种群的生长不可能无限增长,应该会存在一个饱和水平. 当种群增长到接近于饱和水平时,增长速度会逐渐减慢趋近于0,所以玉米植株高度增长应类似于一个S型曲线,而并非呈指数增长.
为什么植株高度不可能一直按指数增长下去呢?你能从现实情境角度给出解释吗?
你能进一步改进这个模型吗?
可以以第9段为界分段描述或者更换函数模型.
若以第9段为界分段描述:
将
代入
,可解得:
所以
此时计算
与真实值
相差不大.
怎样描述总体的误差情况?
能否计算每组函数值与真实值的差,再进行求和?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}生长阶段
1
2
3
4
5
6
植株高度/cm
0.67
1.75
3.69
7.73
16.55
32.55
?
0.90
1.75
3.42
6.68
13.05
25.51
误差
0.23
0
-0.27
-1.05
-3.5
-7.04
生长阶段
7
8
9
10
11
?
植株高度/cm
53.38
97.46
153.6
174.9
180.79
?
?
49.85
97.46
190.40
372.08
727.14
?
误差
-3.53
0
36.8
197.18
546.35
如何避免正负相消?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}生长阶段
1
2
3
4
5
6
植株高度/cm
0.67
1.75
3.69
7.73
16.55
32.55
?
0.90
1.75
3.42
6.68
13.05
25.51
误差
0.23
0
-0.27
-1.05
-3.5
-7.04
生长阶段
7
8
9
10
11
?
植株高度/cm
53.38
97.46
153.6
174.9
180.79
?
?
49.85
97.46
190.40
372.08
727.14
?
误差
-3.53
0
36.8
197.18
546.35
可以计算误差的平方和,来刻画总体的误差情况.
经计算,在h(x)模型下,误差的平方和为338808.
对于
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}生长阶段
1
2
3
4
5
6
植株高度/cm
0.67
1.75
3.69
7.73
16.55
32.55
?
0.90
1.75
3.42
6.68
13.05
25.51
误差
0.23
0
-0.27
-1.05
-3.5
-7.04
生长阶段
7
8
9
10
11
?
植株高度/cm
53.38
97.46
153.6
174.9
180.79
?
?
49.85
97.46
0
-8.34
0
?
误差
-3.53
0
0
69.56
0
经计算,在H(x)模型下,误差的平方和约为145.06.
因此,我们可以通过计算不同模型下误差的平方和来比较模型之间的优劣. 在玉米植株生长规律问题中,
能更好的描述玉米植株高度的变化规律.
也可以考虑更换函数模型. 人们一般用逻辑斯蒂(logistic)模型
来描述类似玉米植株高度的增长规律,这个模型的建立过程需要用到高等数学的知识,大家上大学以后可以对其进行推导. 我们现在可以利用这个模型,选择合适数据,确定其中的三个参数,并将函数值与真实值进行比较,验证模型. 请大家在课后完成.
改进模型
参数求解
建立模型
提出问题
模型检验
我们还可以借助信息技术,如使用数学软件GeoGebra进行函数拟合.
在GeoGebra的表格区中输入玉米植株高度的数据:
点击“双变量回归分析”后,选择“逻辑拟合”:
可以得到利用逻辑斯蒂模型进行函数拟合的结果,同时还可以得到对应函数的解析式:
对于 ,也可以计算相应的误差:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}生长阶段
1
2
3
4
5
6
植株高度/cm
0.67
1.75
3.69
7.73
16.55
32.55
?
0.26
0.68
1.76
4.53
11.41
27.24
误差
-0.41
-1.07
-1.93
-3.20
-5.14
-5.31
生长阶段
7
8
9
10
11
?
植株高度/cm
53.38
97.46
153.6
174.9
180.79
?
?
58.08
102.5
144.88
172.12
185.47
?
误差
4.70
5.04
-8.72
-2.78
4.68
经计算,在F(x)模型下,误差的平方和约为222.98.
抽象、推理和模型是数学的基本思想,学数学最终的目的是应用所学数学知识分析和解决问题.
改进模型
参数求解
建立模型
提出问题
模型检验
实施模型
数学建模活动与之前我们做的文字应用题的区别在于其情境的真实性和条件与问题的开放性. 我们需要了解数学建模的过程与步骤,可以通过数学抽象、数学建模和逻辑推理去解决更多的实际问题.
小结
作业
组建数学建模小组,在以下两个题目中,任选一个进行数学建模实践:
(1)观察特定植物(如葱、水仙花)的生长情况,定期记录有关数据,探索生长规律,并按照类似本节的方法建立对应的生长模型.
(2)了解人口增长规律,查找某一地区或某一国家人口的历史数据,尝试建立相关的数学模型,并利用模型进行预测.
谢谢
