4.1《圆》

学 习 内 容 5.1圆(一) 共 几 课 时 2 课 型
第 几 课 时 1
学 习 目 标 1、理解、掌握圆的定义. 2、经历探索点与圆的位置关系的过程，以及如何确定点和圆的三种位置关系.3、初步渗透数形结合和转化的数学思想，并逐步学会用数学的眼光和运动、集合的观点去认识世界、解决问题.
重 点难 点 学习重点：理解、掌握圆的概念. 学习难点：会确定点和圆的位置关系.
教 学 资 源
预 习 设 计
学 生 活 动 设 计 教 师 导 学 设 计
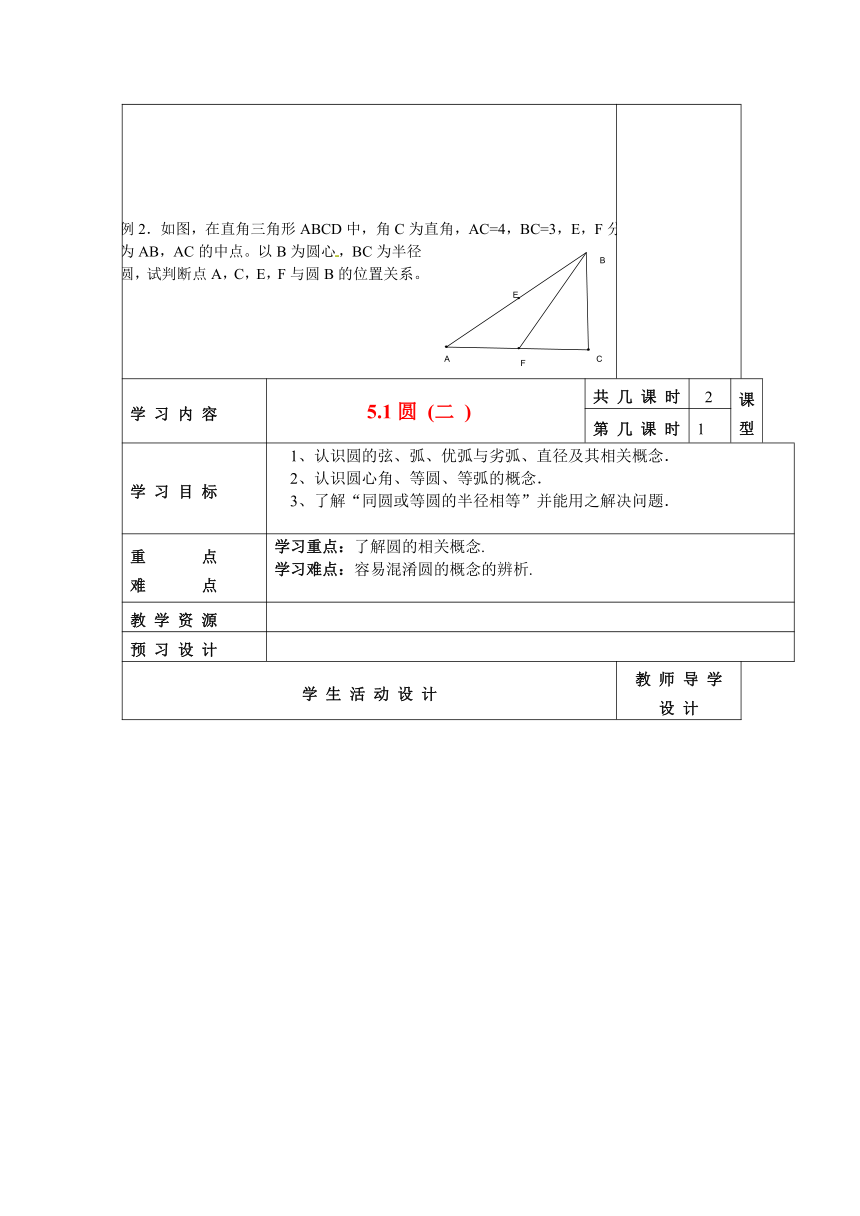
一、情境引入：思考：平面上的一个圆把平面上的点分成哪几部分？二、探究学习：1．尝试：量一量（1）利用圆规画一个⊙O，使⊙O的半径r=3cm.（2）在平面内任意取一点P，点与圆有哪几种位置关系？若⊙O的半径为r，点P到圆心O的距离为d，那么：①点P在圆 d r ②点P在圆 d r ③点P在圆 d 2．概括总结． （1）圆是到定点距离 定长的点的集合.（2）圆的内部是到 的点的集合；（3）圆的外部是 的点的集合 。3.典型例题：例1、已知点P、Q，且PQ=4cm，⑴画出下列图形：到点P的距离等于2cm的点的集合；到点Q的距离等于3cm的点的集合。⑵在所画图中，到点P的距离等于2cm，且到点Q的距离等于3cm的点有几个？请在图中将它们表示出来。⑶在所画图中，到点P的距离小于或等于2cm，且到点Q的距离大于或等于3cm的点的集合是怎样的图形？把它画出来。 例2．如图，在直角三角形ABCD中，角C为直角，AC=4，BC=3，E，F分别为AB，AC的中点。以B为圆心，BC为半径画圆，试判断点A，C，E，F与圆B的位置关系。 适宜的教学情境不但可以提供生动、丰富的学习材料，还可以提供在实践中应用知识的机会，促进知识、技能与体验的连接，促进课内向课外的迁移，让学生在生动的应用和活动中理解所学的知识，了解问题的前因后果和来龙去脉，进一步认识知识的本质，灵活的运用所学的知识去解决实际问题，增长才干。
学 习 内 容 5.1圆 (二 ) 共 几 课 时 2 课 型
第 几 课 时 1
学 习 目 标 1、认识圆的弦、弧、优弧与劣弧、直径及其相关概念．2、认识圆心角、等圆、等弧的概念．3、了解“同圆或等圆的半径相等”并能用之解决问题．
重 点难 点 学习重点：了解圆的相关概念. 学习难点：容易混淆圆的概念的辨析.
教 学 资 源
预 习 设 计
学 生 活 动 设 计 教 师 导 学 设 计
一、情境创设前一节课，学习了圆的有关概念，探索了点与圆的位置关系。这一节课将进一步学习与圆有关的概念，为今后研究圆的有关性质打好基础.二、探究学习1.预习圆的相关概念结合图形逐个介绍半圆、优弧、劣弧、弓形、同心圆、等圆的概念及这些几何元素的表示法。引导学生分析它们之间的区别与联系，如半圆和弧一半圆也是弧，是半个圆周，但弧不一定是半圆，半圆不是优弧也不是劣弧，也不是弓形；直径和弦，是过圆心的特殊弦，但弦不一定都是直径；同圆、等圆、同心圆的区别与联系。2.理解与圆有关概念(1)请在图上画出弦CD，直径AB.并说明___________________________叫做弦；_________________________________叫做直径.(2)弧、半圆、优弧与劣弧的概念及表示方法.弧：____________________________________.半圆：__________________________________________________.优弧：_________________________________,表示方法：________.劣弧：_________________________________,表示方法：________. (3)借助图形理解圆心角、同心圆、等圆.圆心角:_____________________________________.同心圆: _____________________________________.等圆: _____________________________________.(4) 同圆或等圆的半径_______.等弧: ______________________________________________.三、典型例题例. 已知：如图，点A、B和点C、D分别在同心圆上.且∠AOB＝∠COD，∠C与∠D相等吗？为什么？ 适宜的教学情境不但可以提供生动、丰富的学习材料，还可以提供在实践中应用知识的机会，促进知识、技能与体验的连接，促进课内向课外的迁移，让学生在生动的应用和活动中理解所学的知识，了解问题的前因后果和来龙去脉，进一步认识知识的本质，灵活的运用所学的知识去解决实际问题，增长才干。