人教七下数学5.1.2垂线 课件(31张ppt)
文档属性
| 名称 | 人教七下数学5.1.2垂线 课件(31张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-11 00:00:00 | ||
图片预览







文档简介
(共31张PPT)
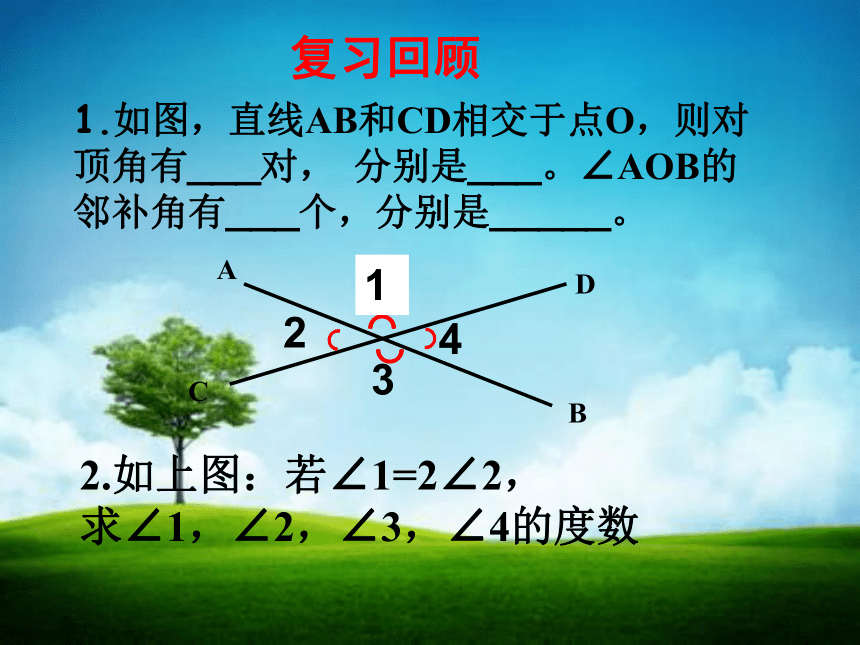
复习回顾
1.如图,直线AB和CD相交于点O,则对顶角有___对,
分别是___。∠AOB的邻补角有___个,分别是_____。
B
O
A
D
C
⌒
⌒
⌒
1
⌒
2
3
4
2.如上图:若∠1=2∠2,
求∠1,∠2,∠3,∠4的度数
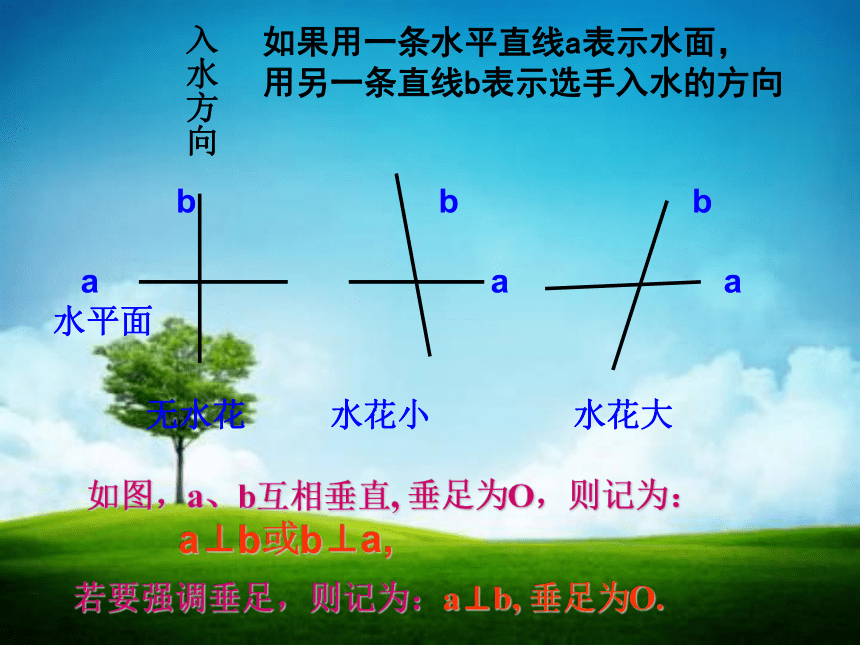
三位跳水运动员入水前的精彩瞬间,哪位运动员溅起的水花小?
b
b
b
a
a
a
水平面
入水方向
无水花
水花小
水花大
如果用一条水平直线a表示水面,
用另一条直线b表示选手入水的方向
如图,a、b互相垂直,
垂足为O,则记为:
a⊥b或b⊥a,
若要强调垂足,则记为:a⊥b,
垂足为O.
1.垂直定义:当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足。
一、垂直的定义
从垂直的定义可知,
判断两条直线互相垂直的关键:
只要找到两条直线相交时四个交角中一个角是直角。
F
E
M
N
O
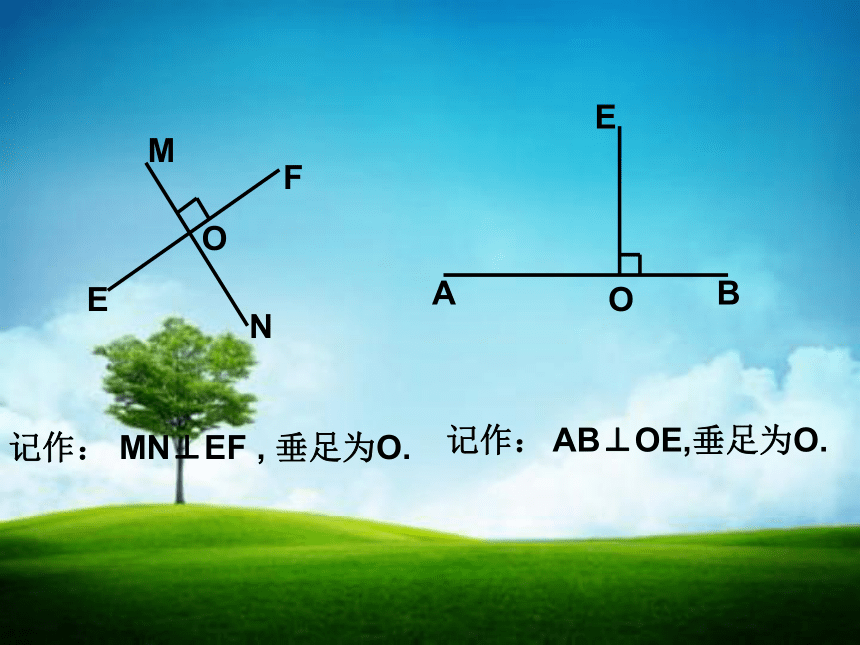
记作:
MN⊥EF
,
垂足为O.
A
B
O
E
记作:
AB⊥OE,垂足为O.
A
B
C
D
O
几何语言
1)∵
∠AOC﹦90°(已知)
AB⊥CD
(垂直的定义)
∴__________
已知AB.CD相交于点O,
3.垂直的书写形式:
如图,当直线AB与CD相交于O点,∠AOC=90°时,AB⊥CD,垂足为O。
几何语言
∵AB⊥CD(已知)
∠COB
﹦90°
(垂直的定义)
A
B
C
D
∴______________
o
3.垂直的书写形式:
反之,若直线AB与CD垂直,
垂足为O,那么,∠AOC=90°
O
D
C
B
A
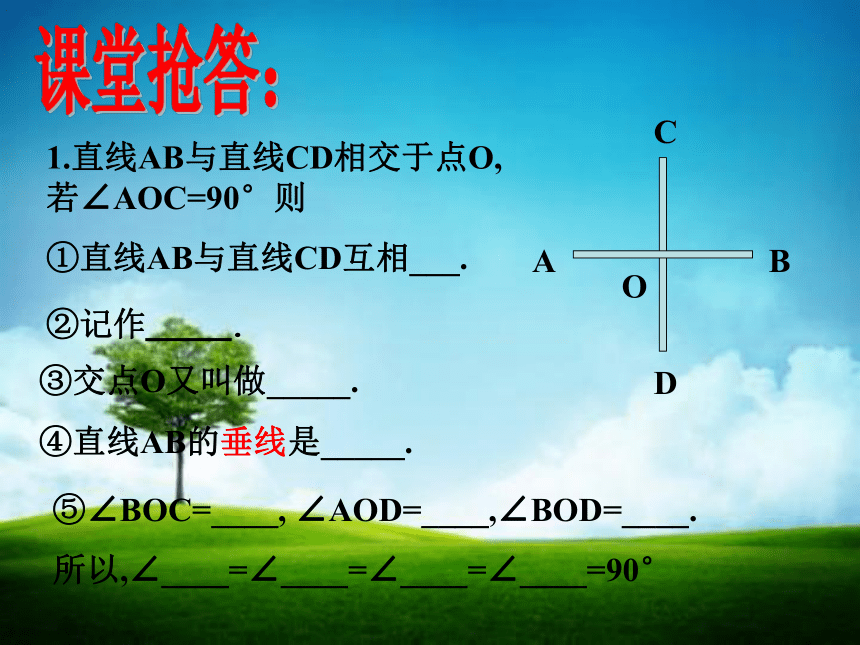
1.直线AB与直线CD相交于点O,若∠AOC=90°则
①直线AB与直线CD互相___.
②记作____.
③交点O又叫做_____.
④直线AB的垂线是_____.
⑤∠BOC=____,
∠AOD=____,∠BOD=____.
所以,∠____=∠____=∠____=∠____=90°
2
.两条直线相交所成的四个角中,下列条件中能判
定两条直线垂直的是(
)
(A)
有两个角相等
(
B)有两对角相等
(C)
有三个角相等
(
D)
有四对邻补角
C
3.下面四种判断两条直线垂直的方法正确的
有(
)个????????????????
(1)两条直线相交所成的四个角中有一个角是直角,则这两条直线互相垂直.
(2)两条直线相交,有一组邻补角相等,则这两条直线互相垂直.
(3)两条直线相交,所成的四个角相等,这两条直线互相垂直.
(4)两条直线相交,有一组对顶角互补,则这两条直线互相垂直.
A.4?????????
B.3????????????
C.2????????????
D.1
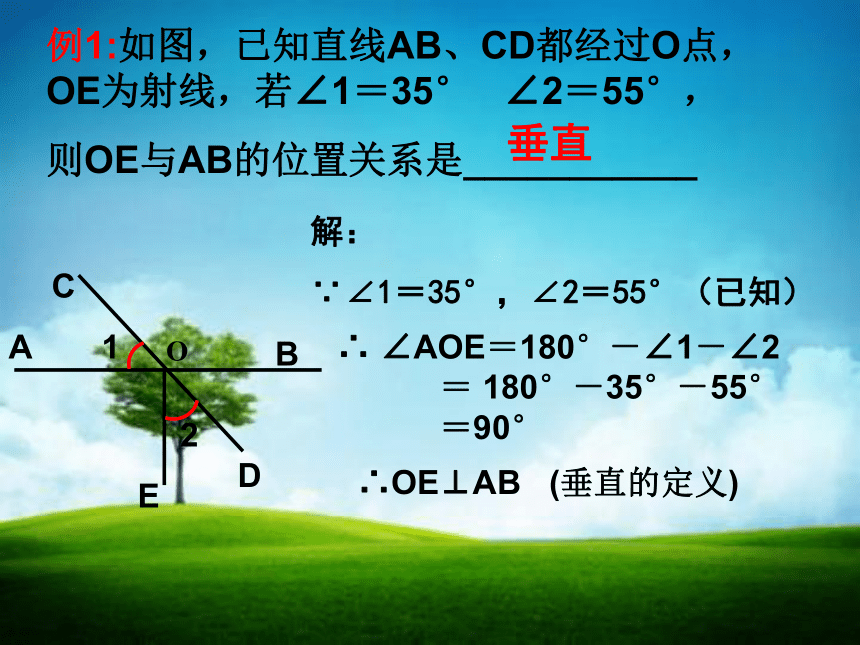
A
解:
∵∠1=35°,∠2=55°(已知)
垂直
∴
∠AOE=180°-∠1-∠2
=
180°-35°-55°
=90°
∴OE⊥AB
(垂直的定义)
例1:如图,已知直线AB、CD都经过O点,OE为射线,若∠1=35°
∠2=55°,
则OE与AB的位置关系是___________
C
D
A
B
O
E
1
2
练习:
1.
如图,直线AB、CD相交于点O,OE⊥AB,∠1=125°,求∠COE的度数.
A
C
E
B
D
O
1
)
2、如图,∠ABC=90°
,∠1=60°
,过B作AC的垂线BO,垂足是O,过O作BC的垂线,垂足是D,若∠1=
∠2,求∠ABO,
∠BOD.
∵BO⊥AC于O点
1
2
A
B
C
D
O
)
)
(已知)
∵∠ABC=90°(
)
∠1=60°(
)
已知
∴∠ABO=30°
解:
(已知)
∴∠BOC=90°
∴∠BOD=30°
(互余的定义)
(互余的定义)
已知
(垂直的定义)
又∵∠2=∠1
∴∠2=60°
(等量代换)
探究:
①用三角尺或量角器画已知直线l
的垂线,这样的垂线能画出几条?
②经过直线l上一点A画
l
的垂线,这样的垂线能画出几条?
③经过直线l
外一点B画
l
的垂线,这样的垂线能画出几条?
二、垂线的画法
垂线的画法:
问题:
这样画l的垂线可以画几条?
1放、
2靠、
3画线、
l
O
如图,已知直线
l,作l的垂线。
工具:直尺、三角板
A
无数条
垂线的画法:
l
A
如图,已知直线
l
和l上的一点A
,作l的垂线.
B
4画线:沿着三角板的另一直角边画出垂线.
1放:放直尺,直尺的一边要与已知直线重合;
3移:移动三角板到已知点;
2靠:靠三角板,把三角板的一直角边靠在直尺上;
则所画直线AB是过点A的直线l的垂线.
结论:过直线上的一点有且只有一条直线与已知直线互相垂直。
垂线的画法:
l
A
如图,已知直线
l
和l外的一点A
,作l的垂线.
B
4画线:沿着三角板的另一直角边画出垂线.
1放:放直尺,直尺的一边要与已知直线重合;
3移:移动三角板到已知点;
2靠:靠三角板,把三角板的一直角边靠在直尺上;
则所画直线AB是经过点A的直线l的垂线.
结论:过直线外一点有且只有一条直线与已知直线垂直.
垂线的性质1:
过一点有且只有一条直线与已知直线垂直.
能作一条,而且只能作一条.
问题:过已知直线
l
和l上(或外)的一点A
,作l的垂线,可以作几条?
注意:
过一点画已知线段(或射线)的垂线,
就是画这条线段(或射线)所在直线的垂线.
课堂练习
1.选择题
过点
向线段
所在直线引垂线,正确的是(
).
A
B
C
D
C
2.画一条线段的垂线,垂足在
(
)
A.线段上
B.线段的端点上
C.线段的延长线上
D.以上都有可能
D
2.如图,请你过点P画出线段AB或射线AB的垂线(画在课本第5页上)
A
·
·
P
回顾复习
1、上节课你学到了什么?
相交线
垂线
垂线性质
垂线画法
2、在这节课中你还有什么疑问?
思考
在灌溉时,要把河中的水引到农田P处,如何挖渠能使渠道最短
连接直线外一点与直线上各点的所有线段中,垂线段最短。
垂线段最短
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
P
A
B
C
m
D
垂线段的长度
简单说成:垂线段最短.
垂线的性质2:
线段AB⊥直线CD,如图,垂足为B,我们就把线段AB叫做点A到直线CD的垂线段。
A
C
D
B
垂线段
垂线与垂线段有何
区别和联系?
注
意:
点A到直线CD的距离是
垂线段AB的长度,而不是垂线段AB。
拓
展
应
用
如图:要把水渠中的水引到水池C中,在渠岸的什么地方开沟,水沟的长度才能最短?
请画出图来,并说明理由。
C
∟
垂线段最短
立定跳远中,体育老师是如何测量运动员的成绩的?
体育老师实际上测量的是点到直线的距离
起跳线
落脚点
小常识
1.直线AB外一点P到直线AB的距离指的是( )
(A)从P点到AB的垂线段
(B)从P点到AB的垂线段长
(C)从P点到AB的垂线(D)从
P点到AB的垂线长
B
巩固练习
2.点P为直线l外一点,点A、B、C在直线l
上,
若PA=4cm,PB=5cm,PC=6cm,则P到直线l
的距离是(
)
A.4cm
B.
小于4cm
C、不大于4cm
D、5cm
C
巩固练习
(1)AB与AC互相垂直;
(2)AD与AC互相垂直;
(3)点C到AB的垂线段是线段AB;
(4)点A到BC的距离是线段AD;
(5)线段AB的长度是点B到AC的距离;
(6)线段AB是点B到AC的距离。
其中正确的有(
)
1个
B.
2个
C.3个
D.
4个
3.
4.如图,
AC⊥BC,
∠C=900
,线段AC、BC、CD中最短的是(
)
(A)
AC
(B)
BC
(C)
CD
(D)
不能确定
D
A
B
C
C
A
B
C
D
E
F
G
M
·
·
问题1:长方体的顶点A处有一只蚂蚁想爬到点C处,请你帮它画出爬行的最佳路线。并说明理由。
问题2:若A处的蚂蚁想爬到棱BC上,你认为它的最佳路线是什么?
问题3:若蚂蚁在点M处,想爬到棱BC上,请你设计一条最佳路线。
┏
N
复习回顾
1.如图,直线AB和CD相交于点O,则对顶角有___对,
分别是___。∠AOB的邻补角有___个,分别是_____。
B
O
A
D
C
⌒
⌒
⌒
1
⌒
2
3
4
2.如上图:若∠1=2∠2,
求∠1,∠2,∠3,∠4的度数
三位跳水运动员入水前的精彩瞬间,哪位运动员溅起的水花小?
b
b
b
a
a
a
水平面
入水方向
无水花
水花小
水花大
如果用一条水平直线a表示水面,
用另一条直线b表示选手入水的方向
如图,a、b互相垂直,
垂足为O,则记为:
a⊥b或b⊥a,
若要强调垂足,则记为:a⊥b,
垂足为O.
1.垂直定义:当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足。
一、垂直的定义
从垂直的定义可知,
判断两条直线互相垂直的关键:
只要找到两条直线相交时四个交角中一个角是直角。
F
E
M
N
O
记作:
MN⊥EF
,
垂足为O.
A
B
O
E
记作:
AB⊥OE,垂足为O.
A
B
C
D
O
几何语言
1)∵
∠AOC﹦90°(已知)
AB⊥CD
(垂直的定义)
∴__________
已知AB.CD相交于点O,
3.垂直的书写形式:
如图,当直线AB与CD相交于O点,∠AOC=90°时,AB⊥CD,垂足为O。
几何语言
∵AB⊥CD(已知)
∠COB
﹦90°
(垂直的定义)
A
B
C
D
∴______________
o
3.垂直的书写形式:
反之,若直线AB与CD垂直,
垂足为O,那么,∠AOC=90°
O
D
C
B
A
1.直线AB与直线CD相交于点O,若∠AOC=90°则
①直线AB与直线CD互相___.
②记作____.
③交点O又叫做_____.
④直线AB的垂线是_____.
⑤∠BOC=____,
∠AOD=____,∠BOD=____.
所以,∠____=∠____=∠____=∠____=90°
2
.两条直线相交所成的四个角中,下列条件中能判
定两条直线垂直的是(
)
(A)
有两个角相等
(
B)有两对角相等
(C)
有三个角相等
(
D)
有四对邻补角
C
3.下面四种判断两条直线垂直的方法正确的
有(
)个????????????????
(1)两条直线相交所成的四个角中有一个角是直角,则这两条直线互相垂直.
(2)两条直线相交,有一组邻补角相等,则这两条直线互相垂直.
(3)两条直线相交,所成的四个角相等,这两条直线互相垂直.
(4)两条直线相交,有一组对顶角互补,则这两条直线互相垂直.
A.4?????????
B.3????????????
C.2????????????
D.1
A
解:
∵∠1=35°,∠2=55°(已知)
垂直
∴
∠AOE=180°-∠1-∠2
=
180°-35°-55°
=90°
∴OE⊥AB
(垂直的定义)
例1:如图,已知直线AB、CD都经过O点,OE为射线,若∠1=35°
∠2=55°,
则OE与AB的位置关系是___________
C
D
A
B
O
E
1
2
练习:
1.
如图,直线AB、CD相交于点O,OE⊥AB,∠1=125°,求∠COE的度数.
A
C
E
B
D
O
1
)
2、如图,∠ABC=90°
,∠1=60°
,过B作AC的垂线BO,垂足是O,过O作BC的垂线,垂足是D,若∠1=
∠2,求∠ABO,
∠BOD.
∵BO⊥AC于O点
1
2
A
B
C
D
O
)
)
(已知)
∵∠ABC=90°(
)
∠1=60°(
)
已知
∴∠ABO=30°
解:
(已知)
∴∠BOC=90°
∴∠BOD=30°
(互余的定义)
(互余的定义)
已知
(垂直的定义)
又∵∠2=∠1
∴∠2=60°
(等量代换)
探究:
①用三角尺或量角器画已知直线l
的垂线,这样的垂线能画出几条?
②经过直线l上一点A画
l
的垂线,这样的垂线能画出几条?
③经过直线l
外一点B画
l
的垂线,这样的垂线能画出几条?
二、垂线的画法
垂线的画法:
问题:
这样画l的垂线可以画几条?
1放、
2靠、
3画线、
l
O
如图,已知直线
l,作l的垂线。
工具:直尺、三角板
A
无数条
垂线的画法:
l
A
如图,已知直线
l
和l上的一点A
,作l的垂线.
B
4画线:沿着三角板的另一直角边画出垂线.
1放:放直尺,直尺的一边要与已知直线重合;
3移:移动三角板到已知点;
2靠:靠三角板,把三角板的一直角边靠在直尺上;
则所画直线AB是过点A的直线l的垂线.
结论:过直线上的一点有且只有一条直线与已知直线互相垂直。
垂线的画法:
l
A
如图,已知直线
l
和l外的一点A
,作l的垂线.
B
4画线:沿着三角板的另一直角边画出垂线.
1放:放直尺,直尺的一边要与已知直线重合;
3移:移动三角板到已知点;
2靠:靠三角板,把三角板的一直角边靠在直尺上;
则所画直线AB是经过点A的直线l的垂线.
结论:过直线外一点有且只有一条直线与已知直线垂直.
垂线的性质1:
过一点有且只有一条直线与已知直线垂直.
能作一条,而且只能作一条.
问题:过已知直线
l
和l上(或外)的一点A
,作l的垂线,可以作几条?
注意:
过一点画已知线段(或射线)的垂线,
就是画这条线段(或射线)所在直线的垂线.
课堂练习
1.选择题
过点
向线段
所在直线引垂线,正确的是(
).
A
B
C
D
C
2.画一条线段的垂线,垂足在
(
)
A.线段上
B.线段的端点上
C.线段的延长线上
D.以上都有可能
D
2.如图,请你过点P画出线段AB或射线AB的垂线(画在课本第5页上)
A
·
·
P
回顾复习
1、上节课你学到了什么?
相交线
垂线
垂线性质
垂线画法
2、在这节课中你还有什么疑问?
思考
在灌溉时,要把河中的水引到农田P处,如何挖渠能使渠道最短
连接直线外一点与直线上各点的所有线段中,垂线段最短。
垂线段最短
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
P
A
B
C
m
D
垂线段的长度
简单说成:垂线段最短.
垂线的性质2:
线段AB⊥直线CD,如图,垂足为B,我们就把线段AB叫做点A到直线CD的垂线段。
A
C
D
B
垂线段
垂线与垂线段有何
区别和联系?
注
意:
点A到直线CD的距离是
垂线段AB的长度,而不是垂线段AB。
拓
展
应
用
如图:要把水渠中的水引到水池C中,在渠岸的什么地方开沟,水沟的长度才能最短?
请画出图来,并说明理由。
C
∟
垂线段最短
立定跳远中,体育老师是如何测量运动员的成绩的?
体育老师实际上测量的是点到直线的距离
起跳线
落脚点
小常识
1.直线AB外一点P到直线AB的距离指的是( )
(A)从P点到AB的垂线段
(B)从P点到AB的垂线段长
(C)从P点到AB的垂线(D)从
P点到AB的垂线长
B
巩固练习
2.点P为直线l外一点,点A、B、C在直线l
上,
若PA=4cm,PB=5cm,PC=6cm,则P到直线l
的距离是(
)
A.4cm
B.
小于4cm
C、不大于4cm
D、5cm
C
巩固练习
(1)AB与AC互相垂直;
(2)AD与AC互相垂直;
(3)点C到AB的垂线段是线段AB;
(4)点A到BC的距离是线段AD;
(5)线段AB的长度是点B到AC的距离;
(6)线段AB是点B到AC的距离。
其中正确的有(
)
1个
B.
2个
C.3个
D.
4个
3.
4.如图,
AC⊥BC,
∠C=900
,线段AC、BC、CD中最短的是(
)
(A)
AC
(B)
BC
(C)
CD
(D)
不能确定
D
A
B
C
C
A
B
C
D
E
F
G
M
·
·
问题1:长方体的顶点A处有一只蚂蚁想爬到点C处,请你帮它画出爬行的最佳路线。并说明理由。
问题2:若A处的蚂蚁想爬到棱BC上,你认为它的最佳路线是什么?
问题3:若蚂蚁在点M处,想爬到棱BC上,请你设计一条最佳路线。
┏
N
