【课时作业】3.3垂径定理(含答案)
文档属性
| 名称 | 【课时作业】3.3垂径定理(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 326.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-11 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2020-2021学年九年级数学下册课时作业(北师版)
第三章 圆
*3 垂径定理
一、选择题
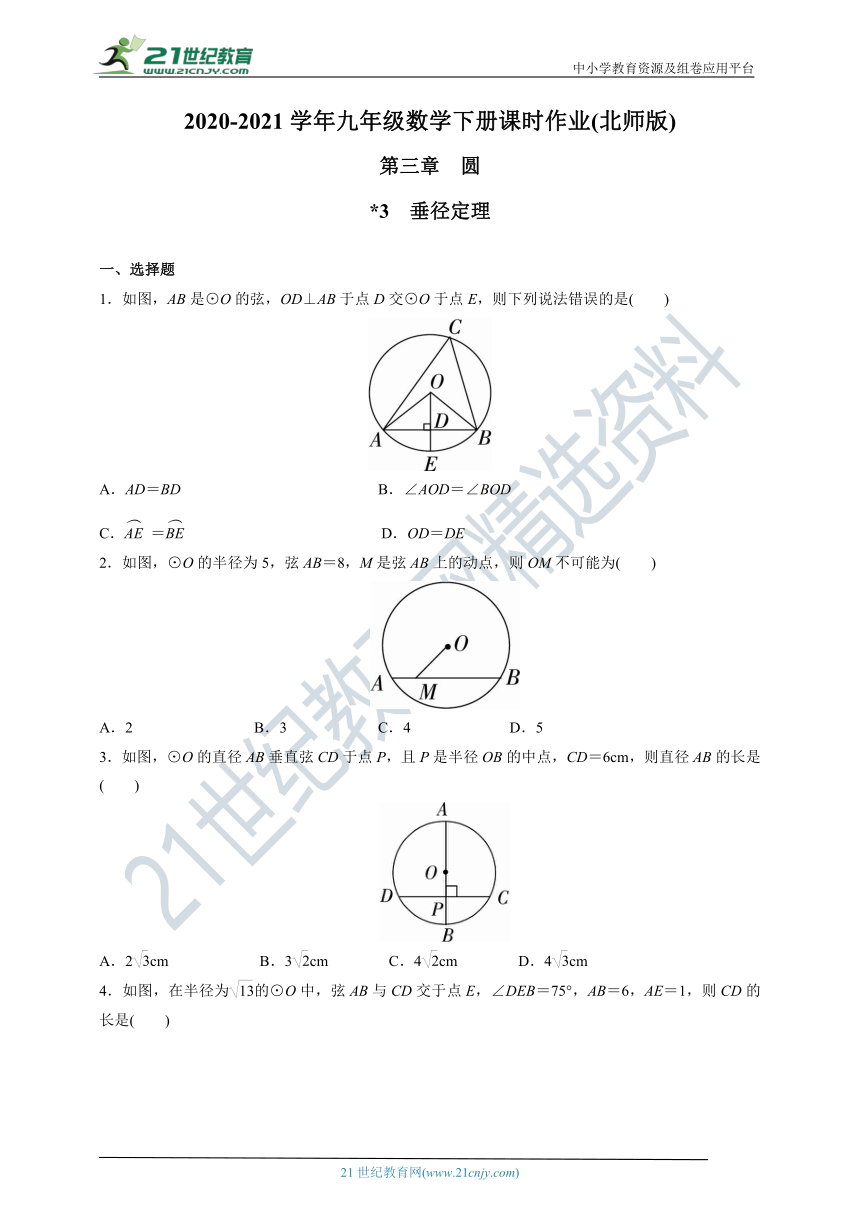
1.如图,AB是⊙O的弦,OD⊥AB于点D交⊙O于点E,则下列说法错误的是( )
A.AD=BD B.∠AOD=∠BOD
C.= D.OD=DE
2.如图,⊙O的半径为5,弦AB=8,M是弦AB上的动点,则OM不可能为( )
A.2 B.3 C.4 D.5
3.如图,⊙O的直径AB垂直弦CD于点P,且P是半径OB的中点,CD=6cm,则直径AB的长是( )
A.2cm B.3cm C.4cm D.4cm
4.如图,在半径为的⊙O中,弦AB与CD交于点E,∠DEB=75°,AB=6,AE=1,则CD的长是( )
A.2 B.2 C.2 D.4
二、填空题
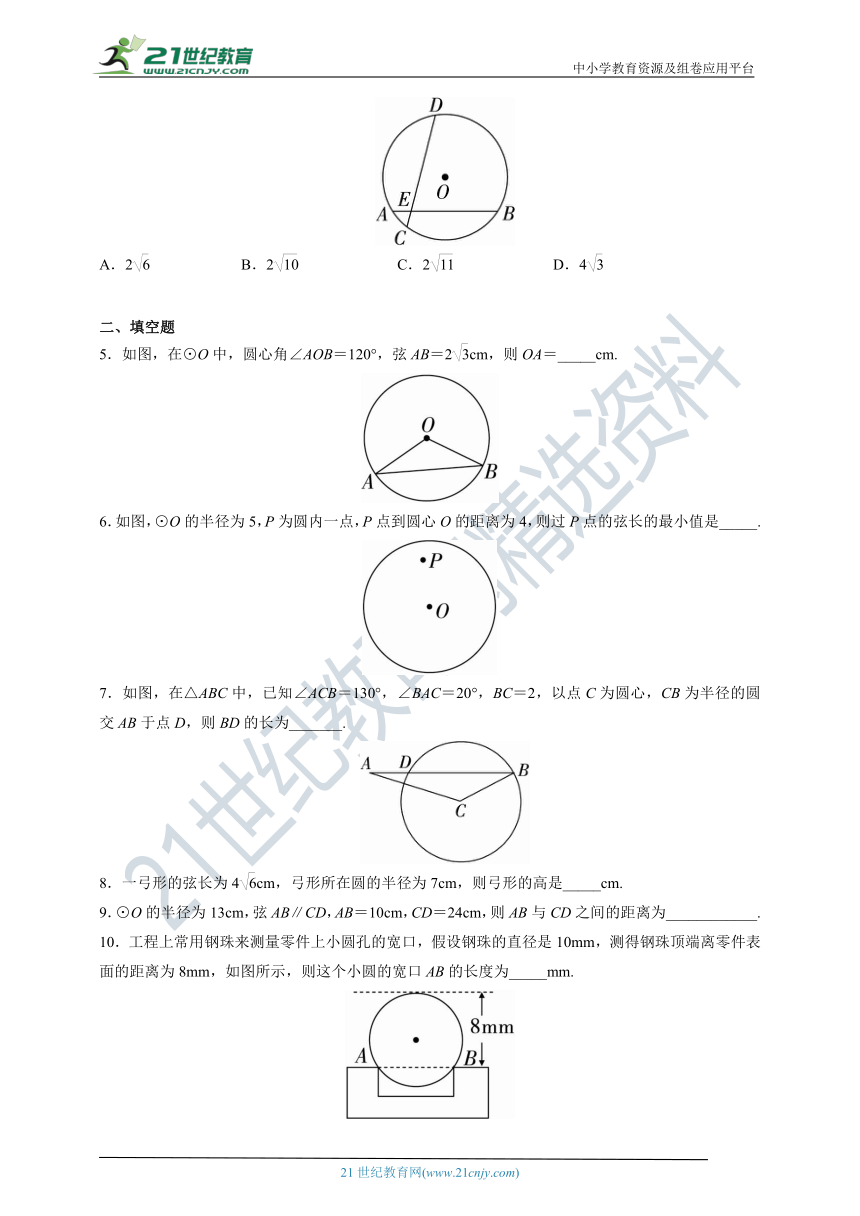
5.如图,在⊙O中,圆心角∠AOB=120°,弦AB=2cm,则OA=_____cm.
6.如图,⊙O的半径为5,P为圆内一点,P点到圆心O的距离为4,则过P点的弦长的最小值是_____.
7.如图,在△ABC中,已知∠ACB=130°,∠BAC=20°,BC=2,以点C为圆心,CB为半径的圆交AB于点D,则BD的长为_______.
8.一弓形的弦长为4cm,弓形所在圆的半径为7cm,则弓形的高是_____cm.
9.⊙O的半径为13cm,弦AB∥CD,AB=10cm,CD=24cm,则AB与CD之间的距离为____________.
10.工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示,则这个小圆的宽口AB的长度为_____mm.
三、解答题
11.如图,M,N分别是⊙O的弦AB,CD的中点,AB=CD.求证:∠AMN=∠CNM.
12.如图,在⊙O中,AB是直径,CD是非直径的弦,且AB⊥CD,P是垂足,若AB=10cm,AP∶PB=4∶1,求CD的长.
13.如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB,BC分别交于点D,E,求AB,AD的长.
14.如图,已知AB为⊙O的弦,从圆上任一点引弦CD⊥AB,作∠OCD的平分线交⊙O于点E,连接EA,EB.求证:EA=EB.
15.某校新建一个圆形花坛.为测量该花坛的半径,小亮和小华沿花坛边选取A,B,C三根木柱,使得A,B之间的距离与A,C之间的距离相等,并测得BC长为24m,A到BC的距离为8m,如图所示.请你帮他们求出这个圆形花坛的半径.
16.如图,在波平如镜的湖面,高出水面半尺的地方长着一朵红莲,它孤零零地直立在那里.突然,一阵狂风吹过,它被吹倒在一边.有一位渔人看见,它现在离原来生长的地方有两尺远.这里的湖水有多深?
17.如图,M是的中点,过点M的弦MN交AB于点C.设⊙O的半径为4cm,MN=4cm.
(1)求圆心O到弦MN的距离;
(2)求∠ACM的度数.
参 考 答 案
1. D 2. A 3. D 4. C
5. 2
6. 6
7. 2
8. 2
9. 7cm或17cm
10. 8
11. 证明:连接OM,ON.∵O为圆心,M,N分别为弦AB,CD的中点,∴OM⊥AB,ON⊥CD.∵AB=CD,∴OM=ON.∴∠OMN=∠ONM.∵∠AMN=90°-∠OMN,∠CNM=90°-∠ONM,∴∠AMN=∠CNM.
12. 解:∵AB=10cm,AP∶PB=4∶1,∴AP=8cm,PB=2cm,AO=BO=5cm,∴OP=AP-AO=3cm.∵AB⊥CD,∴CD=2CP=2PD.由勾股定理得CP=4cm,∴CD=2PC=8cm.
13. 解:∵∠C=90°,AC=3,BC=4,∴AB=5.过点C作CF⊥AB于点F,则有AC·BC=AB·CF,∴CF=2.4,∴AF===1.8,∴AD=2AF=2×1.8=3.6.
14. 证明:连接OE.∵CO=OE,∴∠OCE=∠OEC.又∵CE平分∠OCD,∴∠OCE=∠DCE,∴∠DCE=∠OEC,∴OE∥CD.∵CD⊥AB,∴OE⊥AB,∴=,∴AE=BE.
15. 解:设圆心为点O,连接OB,OA,AB,AC,OA交线段BC于点D.∵AB=AC,∴=.∴OA⊥BC,且BD=DC=BC=12m.由题意,DA=8m.在Rt△BDO中,OB2=OD2+BD2.设OB=xm,则x2=(x-8)2+122,∴x=13.所以这个花坛的半径为13m.
16. 解:如图,AO为直立的红莲,AC为水面上面的部分,且AC=0.5尺.经狂风吹过,红莲AO变成BO,点B在水面上,AO=BO,BC=2尺.设OC=x,则AO=x+0.5=OB.在Rt△BCO中,有(x+0.5)2=x2+22,解得x=3.75.即这里的湖水深3.75尺.
17. 解:(1)连接OM,过点O作OD⊥MN于点D.由垂径定理,得MD=MN=×4=2(cm).在Rt△ODM中,OM=4cm,MD=2cm,∴OD==2cm.故圆心O到弦MN的距离为2cm.
(2)由(1),知在Rt△OMD中,OD=OM,∴∠OMD=30°.又∵点M是的中点,∴OM⊥AB,∴∠ACM=90°-∠OMD=60°.
_21?????????è?????(www.21cnjy.com)_
2020-2021学年九年级数学下册课时作业(北师版)
第三章 圆
*3 垂径定理
一、选择题
1.如图,AB是⊙O的弦,OD⊥AB于点D交⊙O于点E,则下列说法错误的是( )
A.AD=BD B.∠AOD=∠BOD
C.= D.OD=DE
2.如图,⊙O的半径为5,弦AB=8,M是弦AB上的动点,则OM不可能为( )
A.2 B.3 C.4 D.5
3.如图,⊙O的直径AB垂直弦CD于点P,且P是半径OB的中点,CD=6cm,则直径AB的长是( )
A.2cm B.3cm C.4cm D.4cm
4.如图,在半径为的⊙O中,弦AB与CD交于点E,∠DEB=75°,AB=6,AE=1,则CD的长是( )
A.2 B.2 C.2 D.4
二、填空题
5.如图,在⊙O中,圆心角∠AOB=120°,弦AB=2cm,则OA=_____cm.
6.如图,⊙O的半径为5,P为圆内一点,P点到圆心O的距离为4,则过P点的弦长的最小值是_____.
7.如图,在△ABC中,已知∠ACB=130°,∠BAC=20°,BC=2,以点C为圆心,CB为半径的圆交AB于点D,则BD的长为_______.
8.一弓形的弦长为4cm,弓形所在圆的半径为7cm,则弓形的高是_____cm.
9.⊙O的半径为13cm,弦AB∥CD,AB=10cm,CD=24cm,则AB与CD之间的距离为____________.
10.工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示,则这个小圆的宽口AB的长度为_____mm.
三、解答题
11.如图,M,N分别是⊙O的弦AB,CD的中点,AB=CD.求证:∠AMN=∠CNM.
12.如图,在⊙O中,AB是直径,CD是非直径的弦,且AB⊥CD,P是垂足,若AB=10cm,AP∶PB=4∶1,求CD的长.
13.如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB,BC分别交于点D,E,求AB,AD的长.
14.如图,已知AB为⊙O的弦,从圆上任一点引弦CD⊥AB,作∠OCD的平分线交⊙O于点E,连接EA,EB.求证:EA=EB.
15.某校新建一个圆形花坛.为测量该花坛的半径,小亮和小华沿花坛边选取A,B,C三根木柱,使得A,B之间的距离与A,C之间的距离相等,并测得BC长为24m,A到BC的距离为8m,如图所示.请你帮他们求出这个圆形花坛的半径.
16.如图,在波平如镜的湖面,高出水面半尺的地方长着一朵红莲,它孤零零地直立在那里.突然,一阵狂风吹过,它被吹倒在一边.有一位渔人看见,它现在离原来生长的地方有两尺远.这里的湖水有多深?
17.如图,M是的中点,过点M的弦MN交AB于点C.设⊙O的半径为4cm,MN=4cm.
(1)求圆心O到弦MN的距离;
(2)求∠ACM的度数.
参 考 答 案
1. D 2. A 3. D 4. C
5. 2
6. 6
7. 2
8. 2
9. 7cm或17cm
10. 8
11. 证明:连接OM,ON.∵O为圆心,M,N分别为弦AB,CD的中点,∴OM⊥AB,ON⊥CD.∵AB=CD,∴OM=ON.∴∠OMN=∠ONM.∵∠AMN=90°-∠OMN,∠CNM=90°-∠ONM,∴∠AMN=∠CNM.
12. 解:∵AB=10cm,AP∶PB=4∶1,∴AP=8cm,PB=2cm,AO=BO=5cm,∴OP=AP-AO=3cm.∵AB⊥CD,∴CD=2CP=2PD.由勾股定理得CP=4cm,∴CD=2PC=8cm.
13. 解:∵∠C=90°,AC=3,BC=4,∴AB=5.过点C作CF⊥AB于点F,则有AC·BC=AB·CF,∴CF=2.4,∴AF===1.8,∴AD=2AF=2×1.8=3.6.
14. 证明:连接OE.∵CO=OE,∴∠OCE=∠OEC.又∵CE平分∠OCD,∴∠OCE=∠DCE,∴∠DCE=∠OEC,∴OE∥CD.∵CD⊥AB,∴OE⊥AB,∴=,∴AE=BE.
15. 解:设圆心为点O,连接OB,OA,AB,AC,OA交线段BC于点D.∵AB=AC,∴=.∴OA⊥BC,且BD=DC=BC=12m.由题意,DA=8m.在Rt△BDO中,OB2=OD2+BD2.设OB=xm,则x2=(x-8)2+122,∴x=13.所以这个花坛的半径为13m.
16. 解:如图,AO为直立的红莲,AC为水面上面的部分,且AC=0.5尺.经狂风吹过,红莲AO变成BO,点B在水面上,AO=BO,BC=2尺.设OC=x,则AO=x+0.5=OB.在Rt△BCO中,有(x+0.5)2=x2+22,解得x=3.75.即这里的湖水深3.75尺.
17. 解:(1)连接OM,过点O作OD⊥MN于点D.由垂径定理,得MD=MN=×4=2(cm).在Rt△ODM中,OM=4cm,MD=2cm,∴OD==2cm.故圆心O到弦MN的距离为2cm.
(2)由(1),知在Rt△OMD中,OD=OM,∴∠OMD=30°.又∵点M是的中点,∴OM⊥AB,∴∠ACM=90°-∠OMD=60°.
_21?????????è?????(www.21cnjy.com)_
