鲁教九年级(下)综合水平测试
图片预览

文档简介
鲁教九年级(下)综合水平测试
一、选择题(每小题2分,共16分)
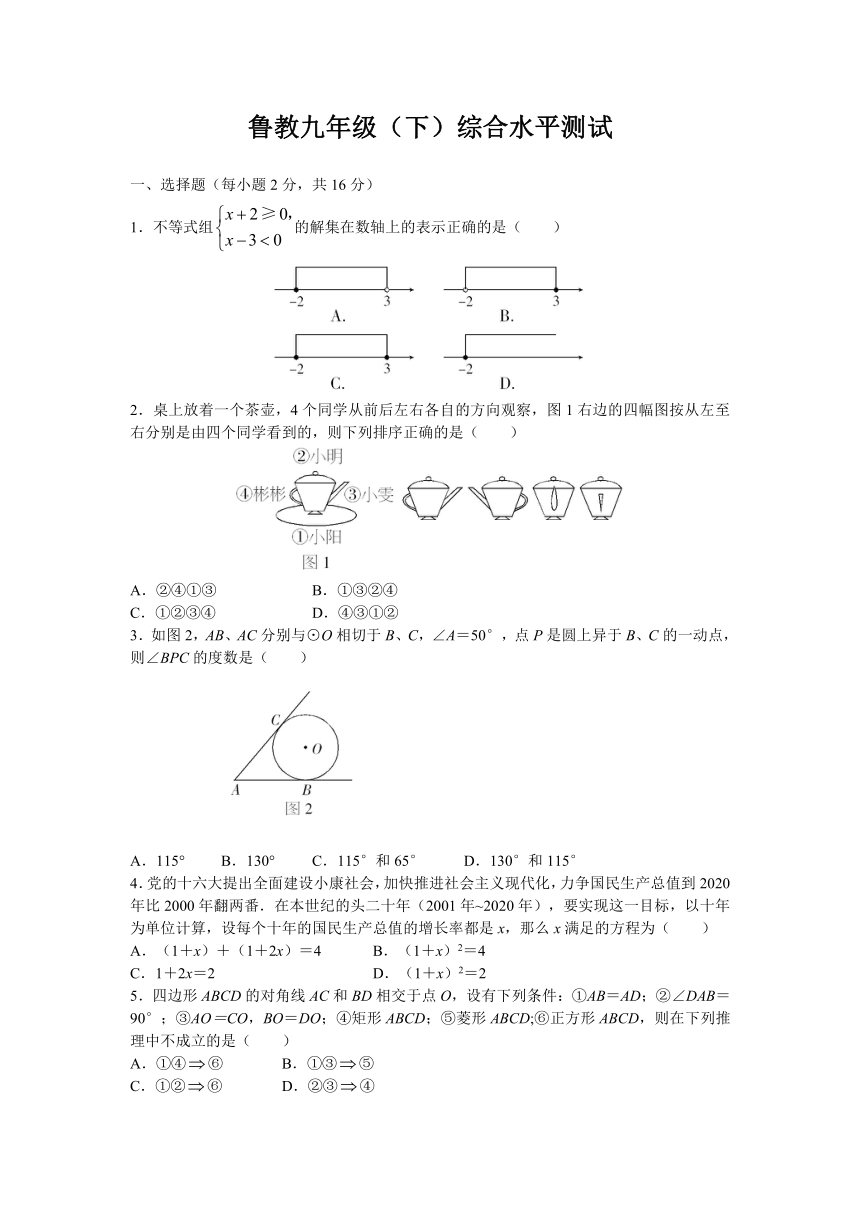
1.不等式组的解集在数轴上的表示正确的是( )
2.桌上放着一个茶壶,4个同学从前后左右各自的方向观察,图1右边的四幅图按从左至右分别是由四个同学看到的,则下列排序正确的是( )
A.②④①③ B.①③②④
C.①②③④ D.④③①②
3.如图2,AB、AC分别与⊙O相切于B、C,∠A=50°,点P是圆上异于B、C的一动点,则∠BPC的度数是( )
A.115° B.130° C.115°和65° D.130°和115°
4.党的十六大提出全面建设小康社会,加快推进社会主义现代化,力争国民生产总值到2020年比2000年翻两番.在本世纪的头二十年(2001年~2020年),要实现这一目标,以十年为单位计算,设每个十年的国民生产总值的增长率都是x,那么x满足的方程为( )
A.(1+x)+(1+2x)=4 B.(1+x)2=4
C.1+2x=2 D.(1+x)2=2
5.四边形ABCD的对角线AC和BD相交于点O,设有下列条件:①AB=AD;②∠DAB=90°;③AO=CO,BO=DO;④矩形ABCD;⑤菱形ABCD;⑥正方形ABCD,则在下列推理中不成立的是( )
A.①④⑥ B.①③⑤
C.①②⑥ D.②③④
6.现选用边长相同的正四边形、正八边形这两种规格的花岗石板料镶地面,则在每一个顶点周围,正四边形、正八边形板铺料的个数分别是( )
A.2,1 B.1,2 C.1,3 D.3,1
7.图3中每个正方形网格都是由四个边长为1的小正方形组成,其中阴影部分的面积是2的图形个数有( )
A.1个 B.2个 C.3个 D.4个
8.一天,小军和爸爸登山,已知山脚到山顶的路程为300m,小军先走了一段路程,爸爸才开始出发,如图4中两条线段分别表示小军和爸爸离开山脚登山的路程s(m)与登山所用的时间t(min)的关系(从爸爸开始登山时计时),根据图象所给的信息,判断下列说法中错误的是( )
A.爸爸登山时,小军已走了50m
B.爸爸走了5min,小军仍在爸爸的前面
C.小军比爸爸晚到山顶
D.爸爸前10min登山的速度比小军的速度慢,10min之后登山的速度比小军的速度快
二、填空题(每小题3分,共24分)
9.一次函数的图象经过一、二、四象限,则k的取值范围是 .
10.如图5,扇形AOB中,∠AOB=60°,OB=4,AC⊥OB于C,以C为圆心CB长为半径画弧交OA于D,则,AD所围成图形的面积是 .
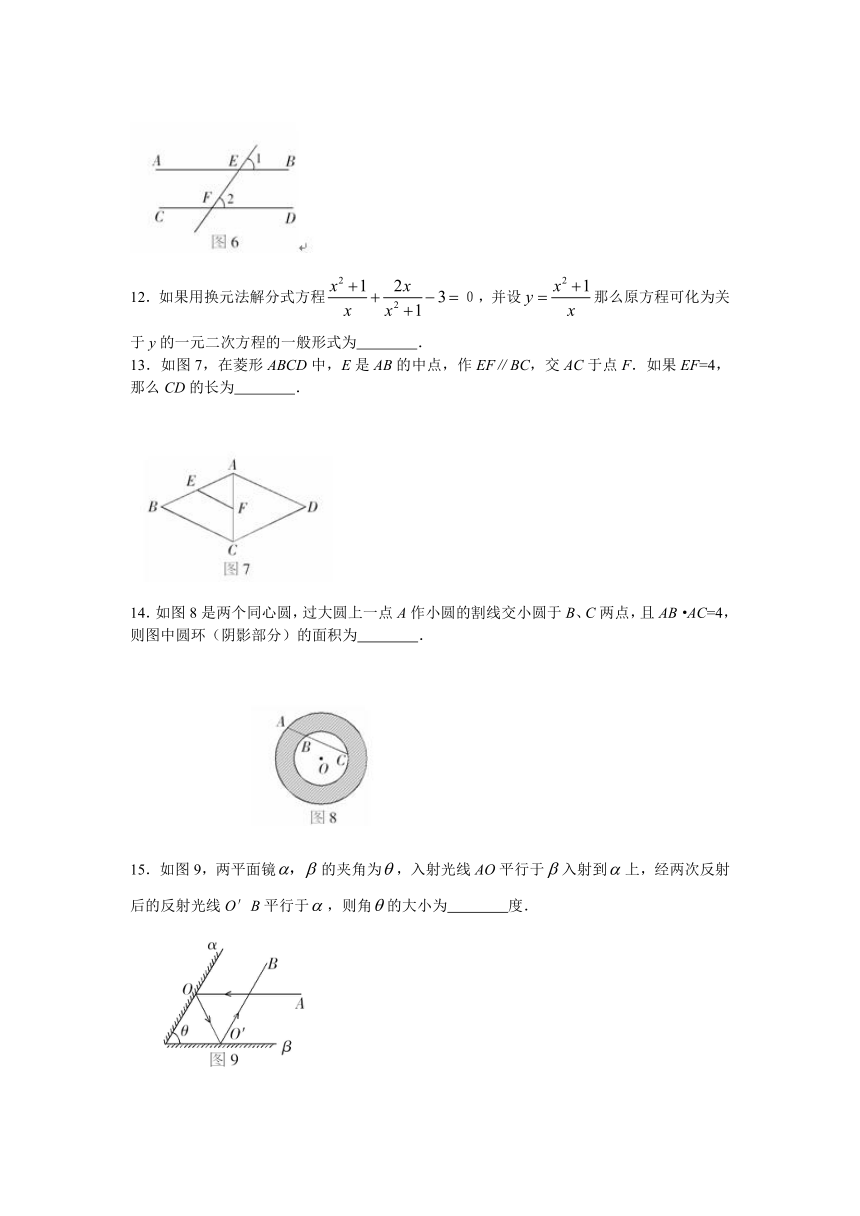
11.如图6,直线AB、CD被直线EF所截,若∠1=∠2,则∠AEF+∠CFE= 度.
12.如果用换元法解分式方程0,并设那么原方程可化为关于y的一元二次方程的一般形式为 .
13.如图7,在菱形ABCD中,E是AB的中点,作EF∥BC,交AC于点F.如果EF=4,那么CD的长为 .
14.如图8是两个同心圆,过大圆上一点A作小圆的割线交小圆于B、C两点,且AB·AC=4,则图中圆环(阴影部分)的面积为 .
15.如图9,两平面镜的夹角为,入射光线AO平行于入射到上,经两次反射后的反射光线O′B平行于,则角的大小为 度.
16.探索规律:31=3,个位数字是3;32=9,个位数字是9;33=27,个位数字是7;34=81,个位数字是1;35=243,个位数字是3;36=729,个位数字是9;……;那么,322的个位数字是 .
三、解答题(共60分)
17.(6分)已知,如图10,在□ABCD中,AB=4cm,AD=7cm,∠ABC的平分线交AD于点E,交CD的延长线于点F,求DF的长.
18.(8分)要在如图11(1)的一个机器零件(尺寸单位:mm)表面涂上防锈漆,请你帮助计算一下这个零件的表面积(其中用r表示底面半径,h表示圆柱的高,l表示圆锥母线.中间过程取准确值,π取3.14,结果保留3个有效数字).
19.(8分)甲、乙、丙三个家电厂在广告中都声称,他们的某种电子产品在正常情况下的使用寿命是8年,经质量检查部门对这三家销售的产品的使用寿命进行跟踪调查,统计结果如下(单位:年):
厂名 使用寿命
甲 4 5 5 5 5 7 9 12 13 15
乙 6 6 8 8 8 9 10 12 14 15
丙 4 4 4 6 7 9 13 15 16 16
(1)请根据题中所给信息,并结合所学统计知识中的有关统计量,说明这三个厂家推销广告中的说法依据是什么?为什么?
(2)如果你是顾客,想选购哪家工厂的产品,为什么?
20.(12分)某饮料厂为了开发新产品,用A、B两种果汁原料各19千克、17.2千克,试制甲、乙两种新型饮料共50千克,下表是试验的相关数据:
每千克含量\饮料 甲 乙
A(单位:千克) 0.5 0.2
B(单位:千克) 0.3 0.4
根据以上信息,解答下列问题:
(1)假设甲种饮料需配制x千克,则乙种饮料需配制 千克;
(2)甲种饮料含A种果汁原料 千克,乙种饮料含A种果汁饮料 千克;
(3)请你写出满足题意的不等式组,并求出其解集.
21.(12分)(1)如图12(甲),边长为1的正△ABC的中心O恰好是扇形OPQ的圆心,要使扇形OPQ绕点O转动,当圆心角∠POQ=120°时,△ABC的面积和周长被扇形OPQ覆盖部分有无变化?若无变化,求出其值是多少?若有变化,请说明理由.
(2)如图12(乙),将甲图中的图形变为边长为1的正方形和圆心角∠POQ=90°的扇形时,正方形的面积和周长被扇形覆盖部分分别为 、 ;
(3)如图12(丙),当甲图中的图形变为边长为1的正五边形和圆心角为 度的扇形时,正五边形的面积和周长被覆盖部分不变;
(4)由(1)(2)(3)中的结论你发现了什么规律,写出你的猜想.
22.(14分)已知Rt△AOB中,∠AOB=90°,OA=3厘米,OB=4厘米,以O为坐标原点建立如图13所示的直角坐标系,设P、Q分别为AB、OB边上的动点,它们同时分别从点A、O向B点匀速运动,运动速度都是1厘米/秒,设P、Q运动时间为t秒(0≤t≤4).
(1)用t表示P点的坐标为 ;
(2)求△OPQ的面积S(cm2)与运动时间t(秒)之间的函数关系式;并求出当t为何值时,S有最大值?S的最大值是多少?
(3)试证明无论t为何值,△OPQ不可能为等边三角形.
(4)当t为 时,△OPQ为直角三角形.
参考答案:
一、1.A
2.C
3.C
4.B
5.C
6.B
7.C
8.D
二、9.
10.
11.180
12.
13.8
14.4π
15.60
16.9
三、17.DF=3cm.
18.这个机器零件的表面积是3.64×104mm2.
19.(1)因为他们采用的特征数不同,甲厂选用了平均数8,乙厂选用了众数8,丙厂选用了中位数8.
(2)选乙厂产品,理由略.
20.(1);
(2);
(3)
解集为28≤x≤30.
21.(1)无变化;(2),1;(3)72;(4)略.
22.(1).
(2)当时,有最大值,最大值是.
(3)略.(4)3秒.
一、选择题(每小题2分,共16分)
1.不等式组的解集在数轴上的表示正确的是( )
2.桌上放着一个茶壶,4个同学从前后左右各自的方向观察,图1右边的四幅图按从左至右分别是由四个同学看到的,则下列排序正确的是( )
A.②④①③ B.①③②④
C.①②③④ D.④③①②
3.如图2,AB、AC分别与⊙O相切于B、C,∠A=50°,点P是圆上异于B、C的一动点,则∠BPC的度数是( )
A.115° B.130° C.115°和65° D.130°和115°
4.党的十六大提出全面建设小康社会,加快推进社会主义现代化,力争国民生产总值到2020年比2000年翻两番.在本世纪的头二十年(2001年~2020年),要实现这一目标,以十年为单位计算,设每个十年的国民生产总值的增长率都是x,那么x满足的方程为( )
A.(1+x)+(1+2x)=4 B.(1+x)2=4
C.1+2x=2 D.(1+x)2=2
5.四边形ABCD的对角线AC和BD相交于点O,设有下列条件:①AB=AD;②∠DAB=90°;③AO=CO,BO=DO;④矩形ABCD;⑤菱形ABCD;⑥正方形ABCD,则在下列推理中不成立的是( )
A.①④⑥ B.①③⑤
C.①②⑥ D.②③④
6.现选用边长相同的正四边形、正八边形这两种规格的花岗石板料镶地面,则在每一个顶点周围,正四边形、正八边形板铺料的个数分别是( )
A.2,1 B.1,2 C.1,3 D.3,1
7.图3中每个正方形网格都是由四个边长为1的小正方形组成,其中阴影部分的面积是2的图形个数有( )
A.1个 B.2个 C.3个 D.4个
8.一天,小军和爸爸登山,已知山脚到山顶的路程为300m,小军先走了一段路程,爸爸才开始出发,如图4中两条线段分别表示小军和爸爸离开山脚登山的路程s(m)与登山所用的时间t(min)的关系(从爸爸开始登山时计时),根据图象所给的信息,判断下列说法中错误的是( )
A.爸爸登山时,小军已走了50m
B.爸爸走了5min,小军仍在爸爸的前面
C.小军比爸爸晚到山顶
D.爸爸前10min登山的速度比小军的速度慢,10min之后登山的速度比小军的速度快
二、填空题(每小题3分,共24分)
9.一次函数的图象经过一、二、四象限,则k的取值范围是 .
10.如图5,扇形AOB中,∠AOB=60°,OB=4,AC⊥OB于C,以C为圆心CB长为半径画弧交OA于D,则,AD所围成图形的面积是 .
11.如图6,直线AB、CD被直线EF所截,若∠1=∠2,则∠AEF+∠CFE= 度.
12.如果用换元法解分式方程0,并设那么原方程可化为关于y的一元二次方程的一般形式为 .
13.如图7,在菱形ABCD中,E是AB的中点,作EF∥BC,交AC于点F.如果EF=4,那么CD的长为 .
14.如图8是两个同心圆,过大圆上一点A作小圆的割线交小圆于B、C两点,且AB·AC=4,则图中圆环(阴影部分)的面积为 .
15.如图9,两平面镜的夹角为,入射光线AO平行于入射到上,经两次反射后的反射光线O′B平行于,则角的大小为 度.
16.探索规律:31=3,个位数字是3;32=9,个位数字是9;33=27,个位数字是7;34=81,个位数字是1;35=243,个位数字是3;36=729,个位数字是9;……;那么,322的个位数字是 .
三、解答题(共60分)
17.(6分)已知,如图10,在□ABCD中,AB=4cm,AD=7cm,∠ABC的平分线交AD于点E,交CD的延长线于点F,求DF的长.
18.(8分)要在如图11(1)的一个机器零件(尺寸单位:mm)表面涂上防锈漆,请你帮助计算一下这个零件的表面积(其中用r表示底面半径,h表示圆柱的高,l表示圆锥母线.中间过程取准确值,π取3.14,结果保留3个有效数字).
19.(8分)甲、乙、丙三个家电厂在广告中都声称,他们的某种电子产品在正常情况下的使用寿命是8年,经质量检查部门对这三家销售的产品的使用寿命进行跟踪调查,统计结果如下(单位:年):
厂名 使用寿命
甲 4 5 5 5 5 7 9 12 13 15
乙 6 6 8 8 8 9 10 12 14 15
丙 4 4 4 6 7 9 13 15 16 16
(1)请根据题中所给信息,并结合所学统计知识中的有关统计量,说明这三个厂家推销广告中的说法依据是什么?为什么?
(2)如果你是顾客,想选购哪家工厂的产品,为什么?
20.(12分)某饮料厂为了开发新产品,用A、B两种果汁原料各19千克、17.2千克,试制甲、乙两种新型饮料共50千克,下表是试验的相关数据:
每千克含量\饮料 甲 乙
A(单位:千克) 0.5 0.2
B(单位:千克) 0.3 0.4
根据以上信息,解答下列问题:
(1)假设甲种饮料需配制x千克,则乙种饮料需配制 千克;
(2)甲种饮料含A种果汁原料 千克,乙种饮料含A种果汁饮料 千克;
(3)请你写出满足题意的不等式组,并求出其解集.
21.(12分)(1)如图12(甲),边长为1的正△ABC的中心O恰好是扇形OPQ的圆心,要使扇形OPQ绕点O转动,当圆心角∠POQ=120°时,△ABC的面积和周长被扇形OPQ覆盖部分有无变化?若无变化,求出其值是多少?若有变化,请说明理由.
(2)如图12(乙),将甲图中的图形变为边长为1的正方形和圆心角∠POQ=90°的扇形时,正方形的面积和周长被扇形覆盖部分分别为 、 ;
(3)如图12(丙),当甲图中的图形变为边长为1的正五边形和圆心角为 度的扇形时,正五边形的面积和周长被覆盖部分不变;
(4)由(1)(2)(3)中的结论你发现了什么规律,写出你的猜想.
22.(14分)已知Rt△AOB中,∠AOB=90°,OA=3厘米,OB=4厘米,以O为坐标原点建立如图13所示的直角坐标系,设P、Q分别为AB、OB边上的动点,它们同时分别从点A、O向B点匀速运动,运动速度都是1厘米/秒,设P、Q运动时间为t秒(0≤t≤4).
(1)用t表示P点的坐标为 ;
(2)求△OPQ的面积S(cm2)与运动时间t(秒)之间的函数关系式;并求出当t为何值时,S有最大值?S的最大值是多少?
(3)试证明无论t为何值,△OPQ不可能为等边三角形.
(4)当t为 时,△OPQ为直角三角形.
参考答案:
一、1.A
2.C
3.C
4.B
5.C
6.B
7.C
8.D
二、9.
10.
11.180
12.
13.8
14.4π
15.60
16.9
三、17.DF=3cm.
18.这个机器零件的表面积是3.64×104mm2.
19.(1)因为他们采用的特征数不同,甲厂选用了平均数8,乙厂选用了众数8,丙厂选用了中位数8.
(2)选乙厂产品,理由略.
20.(1);
(2);
(3)
解集为28≤x≤30.
21.(1)无变化;(2),1;(3)72;(4)略.
22.(1).
(2)当时,有最大值,最大值是.
(3)略.(4)3秒.
同课章节目录
