2020-2021学年人教版八年级下册数学 16.2二次根式的乘除 同步练习(Word版 含解析)
文档属性
| 名称 | 2020-2021学年人教版八年级下册数学 16.2二次根式的乘除 同步练习(Word版 含解析) |
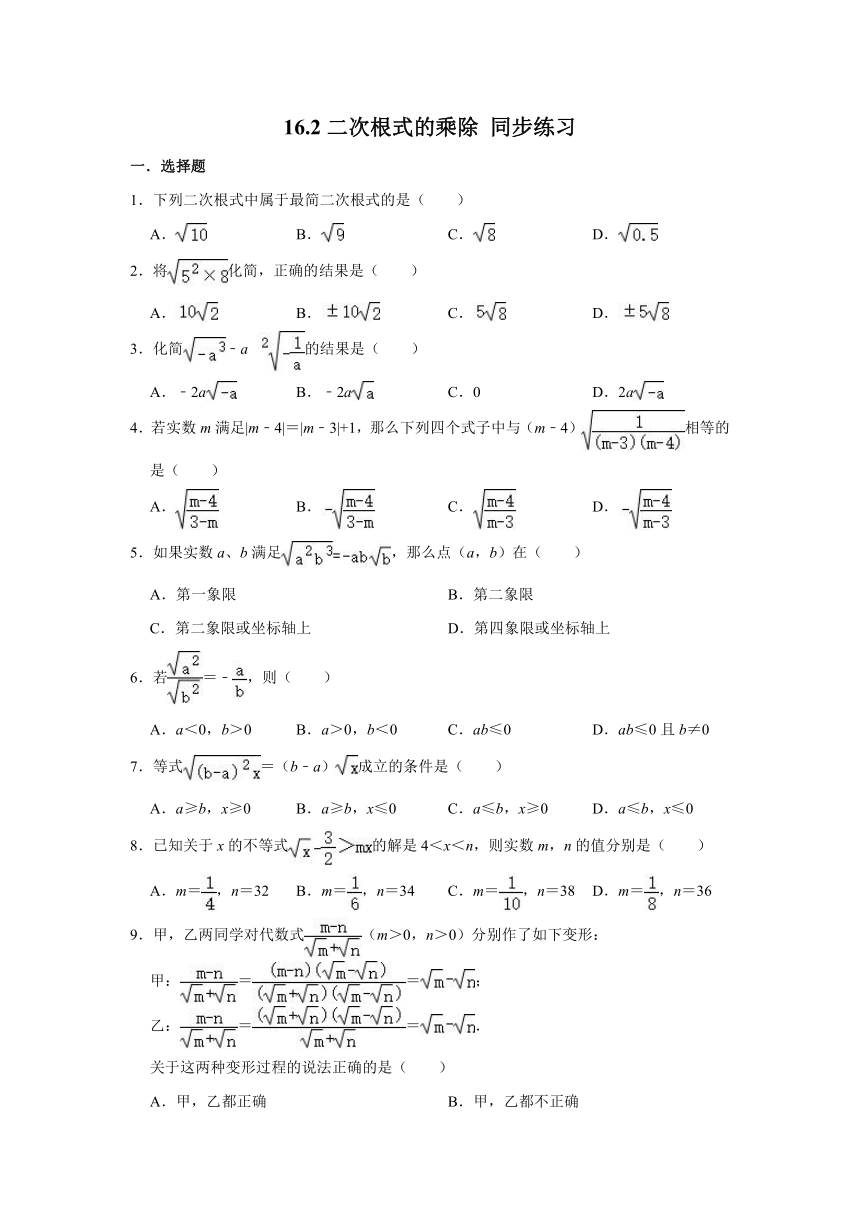
|
|
| 格式 | doc | ||
| 文件大小 | 206.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-11 00:00:00 | ||
图片预览
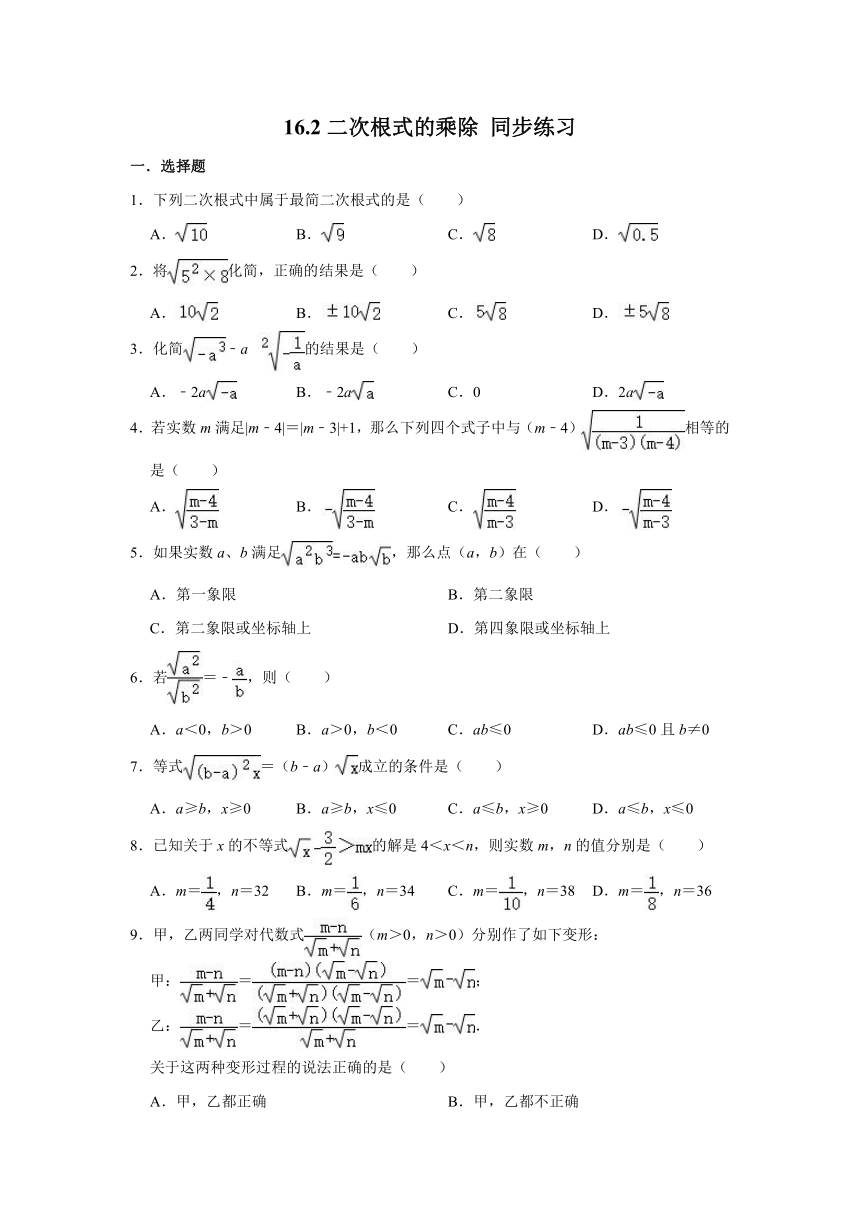


文档简介
16.2二次根式的乘除 同步练习
一.选择题
1.下列二次根式中属于最简二次根式的是( )
A. B. C. D.
2.将化简,正确的结果是( )
A. B. C. D.
3.化简﹣a的结果是( )
A.﹣2a B.﹣2a C.0 D.2a
4.若实数m满足|m﹣4|=|m﹣3|+1,那么下列四个式子中与(m﹣4)相等的是( )
A. B. C. D.
5.如果实数a、b满足,那么点(a,b)在( )
A.第一象限 B.第二象限
C.第二象限或坐标轴上 D.第四象限或坐标轴上
6.若=﹣,则( )
A.a<0,b>0 B.a>0,b<0 C.ab≤0 D.ab≤0且b≠0
7.等式=(b﹣a)成立的条件是( )
A.a≥b,x≥0 B.a≥b,x≤0 C.a≤b,x≥0 D.a≤b,x≤0
8.已知关于x的不等式的解是4<x<n,则实数m,n的值分别是( )
A.m=,n=32 B.m=,n=34 C.m=,n=38 D.m=,n=36
9.甲,乙两同学对代数式(m>0,n>0)分别作了如下变形:
甲:==;
乙:==.
关于这两种变形过程的说法正确的是( )
A.甲,乙都正确 B.甲,乙都不正确
C.只有甲正确 D.只有乙正确
10.计算(1﹣﹣﹣)×(+++)﹣(1﹣﹣﹣﹣)×(++)的结果等于( )
A. B. C. D.
二.填空题
11.化简:____.
12.化简= .
13.计算:××= .
14.若=1,那么x的取值范围是 .
15.下列各式:①=;②=;③=;④=(a>0,b≥0)其中正确的是 (填序号).
三.解答题
16.计算:
17.计算:.
18.小明在学习中发现了一个“有趣”的现象:
∵,①
,②
∴.③
∴2=﹣2.④
(1)上面的推导过程中,从第 步开始出现错误(填序号);
(2)写出该步的正确结果.
19.有这样一类题目:将化简,如果你能找到两个数m、n,使m2+n2=a且mn=,则a±2将变成m2+n2±2mn,即变成(m±n)2,从而使得以化简.例如,因为5+2=3+2+2=()2+()2+2×=(+)2,所以==+.
请仿照上面的例子化简下列根式:
(1);
(2).
参考答案
一.选择题
1.解:A、是最简二次根式,符合题意;
B、=3,不符合题意;
C、=2,不符合题意;
D、=,不符合题意.
故选:A.
2.解:==10,
故选:A.
3.解:﹣a
=﹣a﹣a2?
=﹣a+a
=0.
故选:C.
4.解:由|m﹣4|=|m﹣3|+1得,m≤3,
∴m﹣4<0,m﹣3≤0,
∴(m﹣4)=﹣=﹣.
故选:D.
5.解:∵实数a、b满足,
∴a、b异号,且b>0;
故a<0,或者a、b中有一个为0或均为0.
于是点(a,b)在第二象限或坐标轴上.故选C.
6.解:∵=≥0
又∵=﹣,
∴﹣≥0
∴ab≤0且b≠0
故选:D.
7.解:根据算术平方根的意义可知,b﹣a≥0且x≥0,即a≤b,x≥0.
故选:C.
8.解:∵关于x的不等式的解是4<x<n,
∴方程﹣mx﹣=0的解为4和n,
∴,
∴解得m=,n=36,
故选:D.
9.解:甲的做法是先把分母有理化,再约分,如果m=n则化简不成立;
乙的做法是先把分子分解因式,再约分,正确.故本题选D.
10.解:设a=++,
原式=(1﹣a)(a+)﹣(1﹣a﹣)×a
=a+﹣a2﹣﹣a+a2+
=.
故选:B.
二.填空题
11.解:==
故答案为:.
12.解:由可得a≥0,
所以==5a,
故答案为:5a.
13.解:原式=
=
=
=
=.
故答案为:.
14.解:∵==1,
∴|3x﹣1|=1﹣3x,
∴1﹣3x>0,
解得:x,
故答案为:x<.
15.解:①当a<0,b<0时,与没有意义,故=不正确;
②与没有意义,故=不成立;
③=,正确;
④=(a>0,b≥0)正确;
故答案为:③④.
三.解答题
16.解:原式=5××3=5.
17.解:
=(﹣4÷)
=(﹣4×)
=﹣7.
18.解:(1)上面的推导过程中,从第②步开始出现错误,
故答案为:②;
(2)﹣2=﹣×=﹣=﹣.
19.解:(1)∵4+2=()2+12+2××1=(+1)2,
∴==|+1|=+1,
(2)∵9﹣4=()2+22﹣2××2=(﹣2)2,
∴==|﹣2|=﹣2.
一.选择题
1.下列二次根式中属于最简二次根式的是( )
A. B. C. D.
2.将化简,正确的结果是( )
A. B. C. D.
3.化简﹣a的结果是( )
A.﹣2a B.﹣2a C.0 D.2a
4.若实数m满足|m﹣4|=|m﹣3|+1,那么下列四个式子中与(m﹣4)相等的是( )
A. B. C. D.
5.如果实数a、b满足,那么点(a,b)在( )
A.第一象限 B.第二象限
C.第二象限或坐标轴上 D.第四象限或坐标轴上
6.若=﹣,则( )
A.a<0,b>0 B.a>0,b<0 C.ab≤0 D.ab≤0且b≠0
7.等式=(b﹣a)成立的条件是( )
A.a≥b,x≥0 B.a≥b,x≤0 C.a≤b,x≥0 D.a≤b,x≤0
8.已知关于x的不等式的解是4<x<n,则实数m,n的值分别是( )
A.m=,n=32 B.m=,n=34 C.m=,n=38 D.m=,n=36
9.甲,乙两同学对代数式(m>0,n>0)分别作了如下变形:
甲:==;
乙:==.
关于这两种变形过程的说法正确的是( )
A.甲,乙都正确 B.甲,乙都不正确
C.只有甲正确 D.只有乙正确
10.计算(1﹣﹣﹣)×(+++)﹣(1﹣﹣﹣﹣)×(++)的结果等于( )
A. B. C. D.
二.填空题
11.化简:____.
12.化简= .
13.计算:××= .
14.若=1,那么x的取值范围是 .
15.下列各式:①=;②=;③=;④=(a>0,b≥0)其中正确的是 (填序号).
三.解答题
16.计算:
17.计算:.
18.小明在学习中发现了一个“有趣”的现象:
∵,①
,②
∴.③
∴2=﹣2.④
(1)上面的推导过程中,从第 步开始出现错误(填序号);
(2)写出该步的正确结果.
19.有这样一类题目:将化简,如果你能找到两个数m、n,使m2+n2=a且mn=,则a±2将变成m2+n2±2mn,即变成(m±n)2,从而使得以化简.例如,因为5+2=3+2+2=()2+()2+2×=(+)2,所以==+.
请仿照上面的例子化简下列根式:
(1);
(2).
参考答案
一.选择题
1.解:A、是最简二次根式,符合题意;
B、=3,不符合题意;
C、=2,不符合题意;
D、=,不符合题意.
故选:A.
2.解:==10,
故选:A.
3.解:﹣a
=﹣a﹣a2?
=﹣a+a
=0.
故选:C.
4.解:由|m﹣4|=|m﹣3|+1得,m≤3,
∴m﹣4<0,m﹣3≤0,
∴(m﹣4)=﹣=﹣.
故选:D.
5.解:∵实数a、b满足,
∴a、b异号,且b>0;
故a<0,或者a、b中有一个为0或均为0.
于是点(a,b)在第二象限或坐标轴上.故选C.
6.解:∵=≥0
又∵=﹣,
∴﹣≥0
∴ab≤0且b≠0
故选:D.
7.解:根据算术平方根的意义可知,b﹣a≥0且x≥0,即a≤b,x≥0.
故选:C.
8.解:∵关于x的不等式的解是4<x<n,
∴方程﹣mx﹣=0的解为4和n,
∴,
∴解得m=,n=36,
故选:D.
9.解:甲的做法是先把分母有理化,再约分,如果m=n则化简不成立;
乙的做法是先把分子分解因式,再约分,正确.故本题选D.
10.解:设a=++,
原式=(1﹣a)(a+)﹣(1﹣a﹣)×a
=a+﹣a2﹣﹣a+a2+
=.
故选:B.
二.填空题
11.解:==
故答案为:.
12.解:由可得a≥0,
所以==5a,
故答案为:5a.
13.解:原式=
=
=
=
=.
故答案为:.
14.解:∵==1,
∴|3x﹣1|=1﹣3x,
∴1﹣3x>0,
解得:x,
故答案为:x<.
15.解:①当a<0,b<0时,与没有意义,故=不正确;
②与没有意义,故=不成立;
③=,正确;
④=(a>0,b≥0)正确;
故答案为:③④.
三.解答题
16.解:原式=5××3=5.
17.解:
=(﹣4÷)
=(﹣4×)
=﹣7.
18.解:(1)上面的推导过程中,从第②步开始出现错误,
故答案为:②;
(2)﹣2=﹣×=﹣=﹣.
19.解:(1)∵4+2=()2+12+2××1=(+1)2,
∴==|+1|=+1,
(2)∵9﹣4=()2+22﹣2××2=(﹣2)2,
∴==|﹣2|=﹣2.
