2020_2021学年粤教版高一物理必修2第一章章末总结课件18张PPT
文档属性
| 名称 | 2020_2021学年粤教版高一物理必修2第一章章末总结课件18张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-02-11 00:00:00 | ||
图片预览






文档简介
第一章 章末总结
本节内容:
1、本章思维导图
2、习题讲解
(1)曲线运动的轨迹和合外力的关系
(2)关联速度问题
(3)竖直上抛运动的处理方法:分步骤处理和整体处理。
(4)类平抛运动
抛体运动
规律
竖直方向的抛体运动
竖直上抛运动
竖直下抛运动
模型
定义
规律
模型
定义
斜抛运动
模型
定义
规律
曲线运动
条件:
分类:
研究方法:
关注:小船过河、关联速度问题
平抛运动
模型:
定义:
规律:
一、本章思维导图
抛体运动对比:
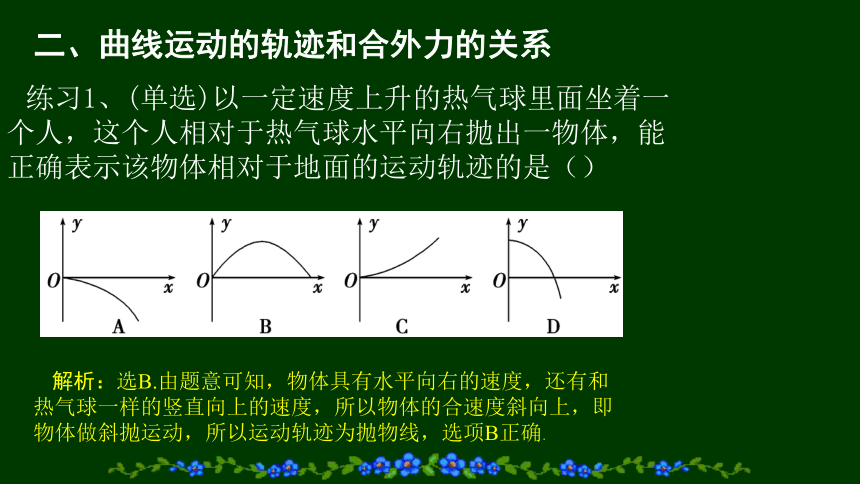
二、曲线运动的轨迹和合外力的关系
练习1、(单选)以一定速度上升的热气球里面坐着一个人,这个人相对于热气球水平向右抛出一物体,能正确表示该物体相对于地面的运动轨迹的是()
解析:选B.由题意可知,物体具有水平向右的速度,还有和热气球一样的竖直向上的速度,所以物体的合速度斜向上,即物体做斜抛运动,所以运动轨迹为抛物线,选项B正确.
方法技巧:
无力不拐弯,拐弯必有力。
两向夹一线,轨迹在中间。
合力指凹侧,曲线向力弯。
三、关联速度问题:
关联物体问题中,如何判断合速度和分速度?
速度怎样分解?
提示:物体的实际运动是合运动;将物体的实际速度分解为垂直于绳(杆)和沿绳(杆)的两个分量.
1、“绳联物体”指物体拉绳(杆)或绳(杆)拉物体的问题(下面为了方便,统一说“绳”),要注意以下两点:
(1)物体的实际速度一定是合速度,分解时两个分速度方向应取沿绳方向和垂直于绳方向.
(2)由于绳不可伸长,一根绳两端物体沿绳方向的速度分量相等.
2.常见的速度分解模型
练习2 如图所示,以速度v沿竖直杆匀速下滑的物体A用轻绳通过定滑轮拉物体B,当绳与水平面夹角为θ时,物体B的速度为( )
练习3 如图所示,AB杆和墙的夹角为θ时,杆的A端沿墙下滑的速度大小为v1,B端沿地面的速度大小为v2,则v1、v2的关系是( )
A.v1=v2 B.v1=v2cos θ
C.v1=v2tan θ D.v1=v2sin θ
C
[可以把A、B两点的速度分解,如图所示,由于杆不能变长或变短,沿杆方向的速度应满足v1x=v2x,即v1cos θ=v2sin θ,v1=v2tan θ,C正确.]
四、竖直上抛运动的处理方法:
分步骤处理、整体处理
练习4、如图,一人站在h=10m高的阳台上将一小球以v0=10m/s的初速度竖直向上抛出,不计空气阻力,g取10m/s2,求小球从抛出到落地所经历的时间。
v0
h
t=(1+3)s
?
五、类平抛运动
练习5、 如图所示,光滑斜面长为a,宽为b,倾角为θ,一小球A沿斜面左上方顶点P水平射入,恰好从下方顶点Q离开斜面,求入射初速度.
解析:小球A在垂直于斜面方向没有运动,小球沿斜面方向上的曲线运动可以分解为水平方向上初速度为v0的匀速直线运动和沿斜面向下初速度为零的匀加速直线运动,物块沿斜面方向的加速度a加=gsin θ.
水平方向b=v0t,
沿斜面方向a=????????????加????????,
由以上各式得:v0=b????sin????????????
?
抛体运动
规律
竖直方向的抛体运动
竖直上抛运动
竖直下抛运动
模型
定义
规律
模型
定义
斜抛运动
模型
定义
规律
曲线运动
条件:
分类:
研究方法:
关注:小船过河、关联速度问题
平抛运动
模型:
定义:
规律:
小结:
本节内容:
1、本章思维导图
2、习题讲解
(1)曲线运动的轨迹和合外力的关系
(2)关联速度问题
(3)竖直上抛运动的处理方法:分步骤处理和整体处理。
(4)类平抛运动
抛体运动
规律
竖直方向的抛体运动
竖直上抛运动
竖直下抛运动
模型
定义
规律
模型
定义
斜抛运动
模型
定义
规律
曲线运动
条件:
分类:
研究方法:
关注:小船过河、关联速度问题
平抛运动
模型:
定义:
规律:
一、本章思维导图
抛体运动对比:
二、曲线运动的轨迹和合外力的关系
练习1、(单选)以一定速度上升的热气球里面坐着一个人,这个人相对于热气球水平向右抛出一物体,能正确表示该物体相对于地面的运动轨迹的是()
解析:选B.由题意可知,物体具有水平向右的速度,还有和热气球一样的竖直向上的速度,所以物体的合速度斜向上,即物体做斜抛运动,所以运动轨迹为抛物线,选项B正确.
方法技巧:
无力不拐弯,拐弯必有力。
两向夹一线,轨迹在中间。
合力指凹侧,曲线向力弯。
三、关联速度问题:
关联物体问题中,如何判断合速度和分速度?
速度怎样分解?
提示:物体的实际运动是合运动;将物体的实际速度分解为垂直于绳(杆)和沿绳(杆)的两个分量.
1、“绳联物体”指物体拉绳(杆)或绳(杆)拉物体的问题(下面为了方便,统一说“绳”),要注意以下两点:
(1)物体的实际速度一定是合速度,分解时两个分速度方向应取沿绳方向和垂直于绳方向.
(2)由于绳不可伸长,一根绳两端物体沿绳方向的速度分量相等.
2.常见的速度分解模型
练习2 如图所示,以速度v沿竖直杆匀速下滑的物体A用轻绳通过定滑轮拉物体B,当绳与水平面夹角为θ时,物体B的速度为( )
练习3 如图所示,AB杆和墙的夹角为θ时,杆的A端沿墙下滑的速度大小为v1,B端沿地面的速度大小为v2,则v1、v2的关系是( )
A.v1=v2 B.v1=v2cos θ
C.v1=v2tan θ D.v1=v2sin θ
C
[可以把A、B两点的速度分解,如图所示,由于杆不能变长或变短,沿杆方向的速度应满足v1x=v2x,即v1cos θ=v2sin θ,v1=v2tan θ,C正确.]
四、竖直上抛运动的处理方法:
分步骤处理、整体处理
练习4、如图,一人站在h=10m高的阳台上将一小球以v0=10m/s的初速度竖直向上抛出,不计空气阻力,g取10m/s2,求小球从抛出到落地所经历的时间。
v0
h
t=(1+3)s
?
五、类平抛运动
练习5、 如图所示,光滑斜面长为a,宽为b,倾角为θ,一小球A沿斜面左上方顶点P水平射入,恰好从下方顶点Q离开斜面,求入射初速度.
解析:小球A在垂直于斜面方向没有运动,小球沿斜面方向上的曲线运动可以分解为水平方向上初速度为v0的匀速直线运动和沿斜面向下初速度为零的匀加速直线运动,物块沿斜面方向的加速度a加=gsin θ.
水平方向b=v0t,
沿斜面方向a=????????????加????????,
由以上各式得:v0=b????sin????????????
?
抛体运动
规律
竖直方向的抛体运动
竖直上抛运动
竖直下抛运动
模型
定义
规律
模型
定义
斜抛运动
模型
定义
规律
曲线运动
条件:
分类:
研究方法:
关注:小船过河、关联速度问题
平抛运动
模型:
定义:
规律:
小结:
同课章节目录
- 第一章 抛体运动
- 第01节 什么是抛体运动
- 第02节 运动的合成与分解
- 第03节 竖直方向的抛体运动
- 第04节 平抛运动
- 第05节 斜抛运动
- 第二章 圆周运动
- 第01节 匀速圆周运动
- 第02节 向心力
- 第03节 离心现象及其应用
- 第三章 万有引力定律及其应用
- 第01节 万有引力定律
- 第02节 万有引力定律的应用
- 第03节 飞向太空
- 第四章 机械能和能源
- 第01节 功
- 第02节 动能 势能
- 第03节 探究外力做功与物体动能变化的关系
- 第04节 机械能守恒定律
- 第05节 验证机械能守恒定律
- 第06节 能量 能量转化与守恒定律
- 第07节 功率
- 第08节 能源的开发与利用
- 第五章 经典力学与物理学的革命
- 第01节 经典力学的成就与局限性
- 第02节 经典时空观与相对论时空观
- 第03节 量子化现象
- 第04节 物理学——人类文明进步的阶梯
