人教版八年级下册17.1勾股定理 课件(21张)
文档属性
| 名称 | 人教版八年级下册17.1勾股定理 课件(21张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-11 00:00:00 | ||
图片预览






文档简介
勾股定理 1
一只老鹰停在5米高树上,离树底不远处草地上有两只兔子,老鹰若想捕食兔子,则它飞行的最短距离是多少?(兔子未察觉)
5
12
?
根据条件能够测量的距离有哪些?
5
12
?
我们需要知道直角三角形三边
的数量关系,即这节课我们要研究
的问题。
一、 画一画
(1)动手画一个直角边长为3cm和4cm的直角,量一量斜边的长度 。
(2)再动手画一个等腰直角三角形,使得
两腰长为2cm,量一量斜边的长度。
量得斜边为5cm
量得斜边约为2.8cm或是2.9cm或是3cm
第一题数据准确吗?第二题哪个数据更准确点呢?
以第二个等腰直角三角形的三边为边向外作三个正方形,探究这三个正方形的面积之间有什么关系。
二、做一做 算一算
a
b
c
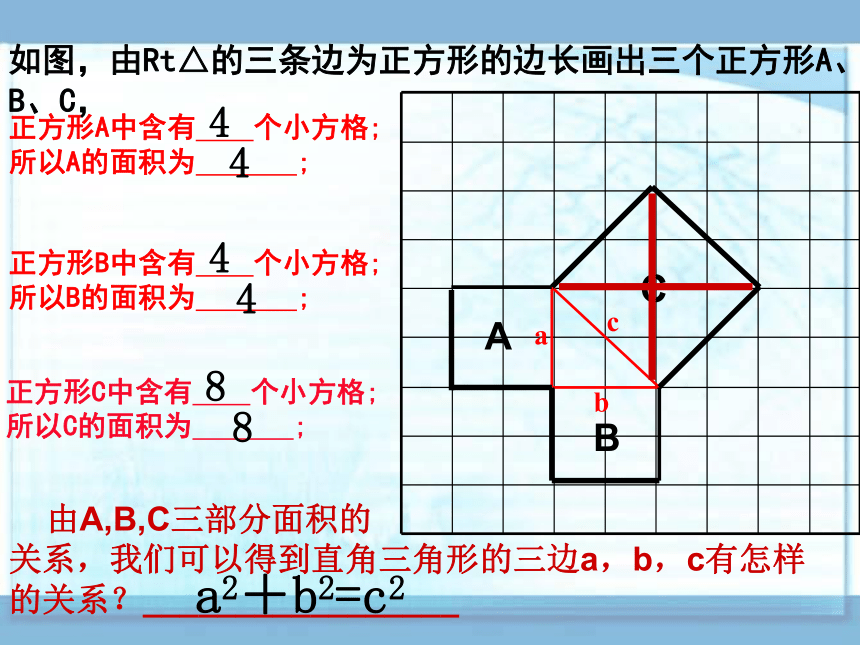
正方形A中含有 个小方格;
所以A的面积为 ;
A
B
C
正方形B中含有 个小方格;
所以B的面积为 ;
正方形C中含有 个小方格;
所以C的面积为 ;
4
4
4
4
8
8
如图,由Rt△的三条边为正方形的边长画出三个正方形A、B、C,
由A,B,C三部分面积的
关系,我们可以得到直角三角形的三边a,b,c有怎样
的关系?_________________
a2+b2=c2
A
B
C
b
a
c
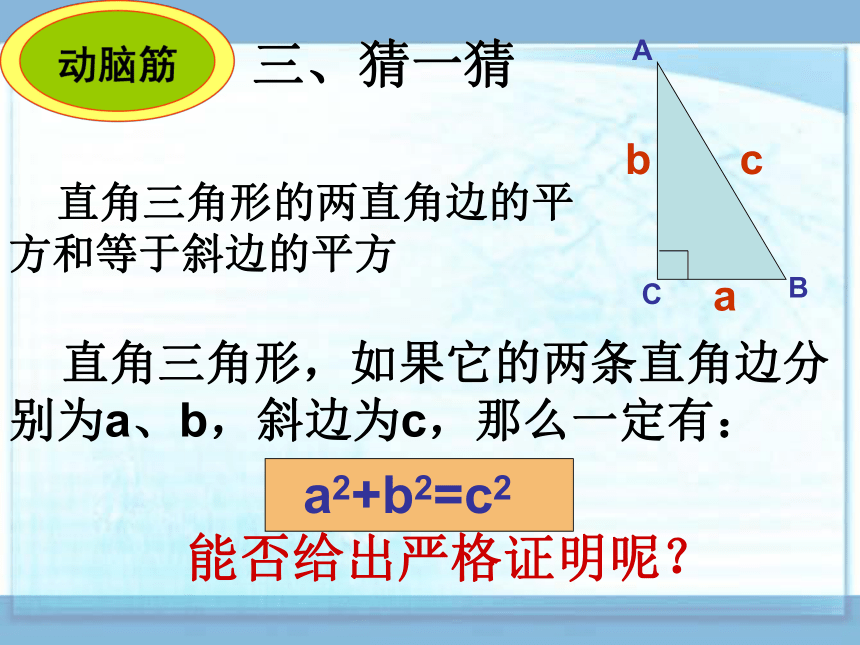
直角三角形,如果它的两条直角边分别为a、b,斜边为c,那么一定有:
a2+b2=c2
三、猜一猜
直角三角形的两直角边的平
方和等于斜边的平方
能否给出严格证明呢?
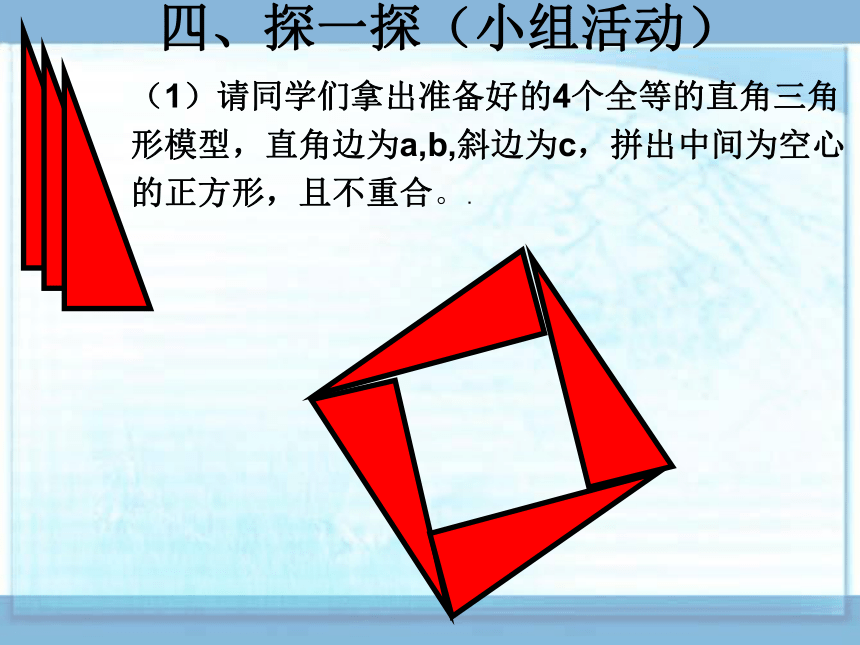
四、探一探(小组活动)
(1)请同学们拿出准备好的4个全等的直角三角
形模型,直角边为a,b,斜边为c,拼出中间为空心
的正方形,且不重合。.
赵爽玄图
2002年国际数学家大会会标
化简得a2+b2=c2
C
b
a
a
b
b
a
b
C
C
C
第一个图中,我们如何求
大正方形的面积?
S大正=c2
S大正= 4S△+S小正
A
B
C
b
a
c
对于任意的直角三角形,如果它的两条直角边分别为a、b,斜边为c,那么一定有:
a2+b2=c2
直角三角形两直角边平方和,
等于斜边的平方。
五、
勾股定理揭示了直角三角形三边的数量关系。
勾股定理
变形
∠C=900 ,c2=a2+b2 ,
b2=c2_a2
两千多年前,古希腊有个哥拉
斯学派,他们首先发现了勾股定理,因此
在国外人们通常称勾股定理为毕达哥拉斯
年希腊曾经发行了一枚纪念票。
定理。为了纪念毕达哥拉斯学派,1955
勾 股 世 界
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前
两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。
六、勾股定理的简单应用
例1(1)在△ABC中,已知a=6, b=8,求c
不可求
勾股定理只适应于直角三角形
六、勾股定理的简单应用
c2=a2 + b2
∠C=900 ,
(2)在△ABC中,已知∠C=900 a=6,b=8, 求斜边c。
已知直角三角形的两直角边,可
用勾股定理求斜边。
六、勾股定理的简单应用
c2=a2 + b2
a2=c2-b2
∠C=900 ,
(3)在直角△ABC中,已知∠B= 900
AB=2,AC=3,求BC边的长。
已知直角三角形的斜边和一条直角
边,可用勾股定理求另一条直角边,
但要注意哪个角是直角
a=5
b=12
C=?
C
A
B
引例
解:因为∠C=900 ,
c2=a2 + b2 =
所以c=13
答:老鹰飞行的最短距离为13m
由勾股定理得
课堂小结
(1)本堂课学了什么定理,解 决了什么问题?
(2)定理在应用时要注意什么?
七
八 作业布置
1、教科书第97页练习
2、查资料找勾股定理其他证法。
谢谢指导!
再见!
再见!
一只老鹰停在5米高树上,离树底不远处草地上有两只兔子,老鹰若想捕食兔子,则它飞行的最短距离是多少?(兔子未察觉)
5
12
?
根据条件能够测量的距离有哪些?
5
12
?
我们需要知道直角三角形三边
的数量关系,即这节课我们要研究
的问题。
一、 画一画
(1)动手画一个直角边长为3cm和4cm的直角,量一量斜边的长度 。
(2)再动手画一个等腰直角三角形,使得
两腰长为2cm,量一量斜边的长度。
量得斜边为5cm
量得斜边约为2.8cm或是2.9cm或是3cm
第一题数据准确吗?第二题哪个数据更准确点呢?
以第二个等腰直角三角形的三边为边向外作三个正方形,探究这三个正方形的面积之间有什么关系。
二、做一做 算一算
a
b
c
正方形A中含有 个小方格;
所以A的面积为 ;
A
B
C
正方形B中含有 个小方格;
所以B的面积为 ;
正方形C中含有 个小方格;
所以C的面积为 ;
4
4
4
4
8
8
如图,由Rt△的三条边为正方形的边长画出三个正方形A、B、C,
由A,B,C三部分面积的
关系,我们可以得到直角三角形的三边a,b,c有怎样
的关系?_________________
a2+b2=c2
A
B
C
b
a
c
直角三角形,如果它的两条直角边分别为a、b,斜边为c,那么一定有:
a2+b2=c2
三、猜一猜
直角三角形的两直角边的平
方和等于斜边的平方
能否给出严格证明呢?
四、探一探(小组活动)
(1)请同学们拿出准备好的4个全等的直角三角
形模型,直角边为a,b,斜边为c,拼出中间为空心
的正方形,且不重合。.
赵爽玄图
2002年国际数学家大会会标
化简得a2+b2=c2
C
b
a
a
b
b
a
b
C
C
C
第一个图中,我们如何求
大正方形的面积?
S大正=c2
S大正= 4S△+S小正
A
B
C
b
a
c
对于任意的直角三角形,如果它的两条直角边分别为a、b,斜边为c,那么一定有:
a2+b2=c2
直角三角形两直角边平方和,
等于斜边的平方。
五、
勾股定理揭示了直角三角形三边的数量关系。
勾股定理
变形
∠C=900 ,c2=a2+b2 ,
b2=c2_a2
两千多年前,古希腊有个哥拉
斯学派,他们首先发现了勾股定理,因此
在国外人们通常称勾股定理为毕达哥拉斯
年希腊曾经发行了一枚纪念票。
定理。为了纪念毕达哥拉斯学派,1955
勾 股 世 界
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前
两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。
六、勾股定理的简单应用
例1(1)在△ABC中,已知a=6, b=8,求c
不可求
勾股定理只适应于直角三角形
六、勾股定理的简单应用
c2=a2 + b2
∠C=900 ,
(2)在△ABC中,已知∠C=900 a=6,b=8, 求斜边c。
已知直角三角形的两直角边,可
用勾股定理求斜边。
六、勾股定理的简单应用
c2=a2 + b2
a2=c2-b2
∠C=900 ,
(3)在直角△ABC中,已知∠B= 900
AB=2,AC=3,求BC边的长。
已知直角三角形的斜边和一条直角
边,可用勾股定理求另一条直角边,
但要注意哪个角是直角
a=5
b=12
C=?
C
A
B
引例
解:因为∠C=900 ,
c2=a2 + b2 =
所以c=13
答:老鹰飞行的最短距离为13m
由勾股定理得
课堂小结
(1)本堂课学了什么定理,解 决了什么问题?
(2)定理在应用时要注意什么?
七
八 作业布置
1、教科书第97页练习
2、查资料找勾股定理其他证法。
谢谢指导!
再见!
再见!
