人教版八年级数学下册同步练习第20章《数据的分析》(Word版 含答案)
文档属性
| 名称 | 人教版八年级数学下册同步练习第20章《数据的分析》(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 59.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-12 00:00:00 | ||
图片预览



文档简介
人教版八年级数学下册同步练习
第20章《数据的分析》
?
1.
数据的平均数是,则这组数据的中位数是?
?
?
?
A.
B.
C.
D.
2.
一组数据为,,,,,,某同学在抄题的时候,误将其中的一个抄成了,那么该同学所抄的数据和原数据相比,不变的统计量是(?
?
?
?
)
A.极差
B.平均数
C.中位数
D.众数?
3.
数据,,,,的方差是(?
?
?
?
)
A.
B.
C.
D.?
4.
立定跳远是体育中考选考项目之一,体育课上老师记录了某同学的一组立定跳远成绩如表:
则下列关于这组数据的说法,正确的是(?
?
?
?
)
A.众数是
B.平均数是
C.中位数是
D.方差是
5.
,,,,,这六个数的平均数是,则的值为(?
?
?
?
)
A.
B.
C.
D.?
6.
校舞蹈队名队员的年龄情况统计如下表,则校舞蹈队队员年龄的众数是(?
?
?
?
)
年龄(岁)
人数(名)
A.
B.
C.
D.?
7.
某青年球队名队员年龄情况如下:,,,,,,,,,.则这名队员年龄的众数、中位数分别是(????????)
A.,
B.,
C.,
D.,
8.
为了比较甲乙两种水稻秧苗谁出苗更整齐,每种秧苗各随机抽取株,分别量出每株高度,发现甲、乙两种秧苗的平均高度一样,方差分别是和,则下列说法正确的是(?
?
?
?
)
A.甲、乙出苗一样整齐
B.甲秧苗出苗更整齐
C.乙秧苗出苗更整齐
D.无法确定甲、乙出苗谁更整齐
9.
某“中学生暑期环保组”的同学,随机调查了“幸福小区”户家庭一周内使用环保方便袋的数量,数据如下(单位:只):,,,,,,,,,.利用上述数据估计该小区户家庭一周内需要环保方便袋约(?
?
?
?
)
A.只
B.只
C.只
D.只
?
10.
已知一组数据,,,,,它的平均数是,这组数据的方差是________.
?
11.
某校九年级学生参加体育测试,其中人的引体向上成绩如下表:
完成引体向上的个数
人?数
这人完成引体向上个数的中位数是________.?
12.
为调查某班每周课外阅读时长,现抽取其中名同学的阅读时长进行了统计,并整理成下表.
阅读时长/h
15
20
25
30
人数/人
1
x
y
2
若这名同学每周课外阅读的平均时长为,中位数是,众数是,则________.
13.
已知一组数据,,,,的平均数是,方差是,则数据,,,,的方差是________.
?
14.
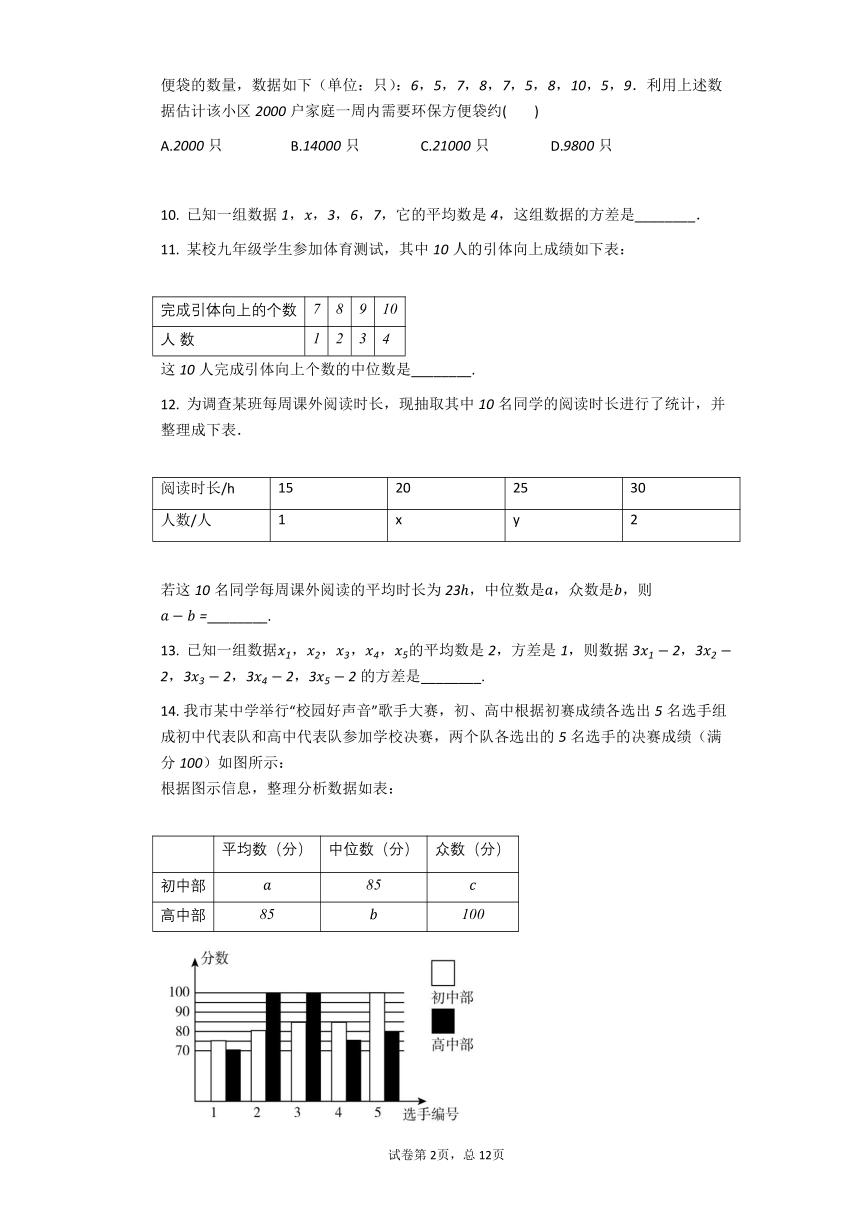
我市某中学举行“校园好声音”歌手大赛,初、高中根据初赛成绩各选出名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的名选手的决赛成绩(满分)如图所示:
根据图示信息,整理分析数据如表:
平均数(分)
中位数(分)
众数(分)
初中部
高中部
求出表格中,,;
小明同学已经算出高中代表队决赛成绩的方差是,请你计算出初中代表队决赛成绩的方差,并判断哪一个代表队选手成绩较为稳定.
?
15.
某校要从甲、乙两名队员中选派一人参加射击比赛,甲、乙两名队员在相同的条件下各射击次,每次命中的环数如下表所示.
次数
①
②
③
④
⑤
⑥
⑦
⑧
⑨
⑩
甲成绩(环数)
乙成绩(环数)
已知甲、乙两名队员的射击成绩的平均成绩相等,请补齐乙的成绩.
甲运动员射击训练成绩的众数是________,中位数是________.
求甲、乙两名队员的射击成绩的方差分别是多少?根据计算结果,从平均数和方差的角度分析,谁将被选中.
?
16.
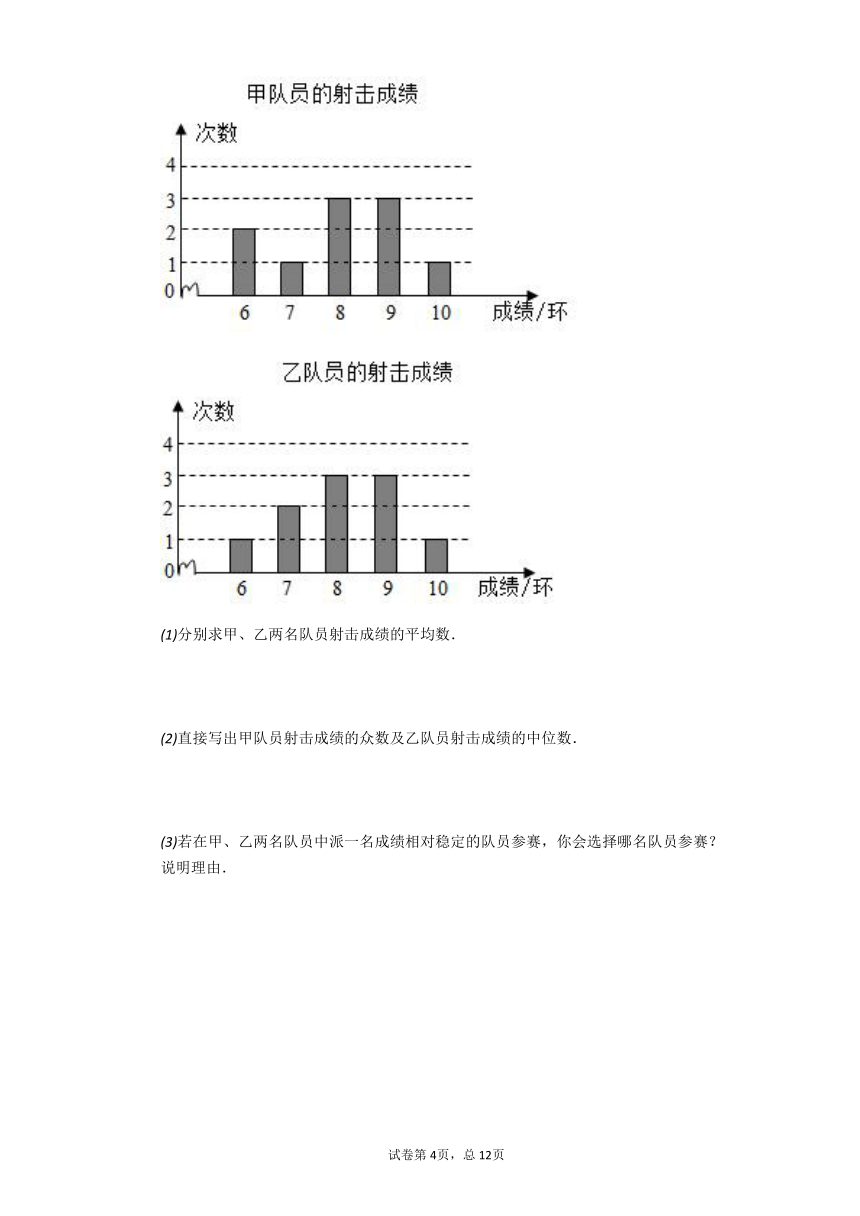
甲、乙两名队员在相同的条件下各射击次,他们的射击成绩(单位:环)如图所示.
分别求甲、乙两名队员射击成绩的平均数.
直接写出甲队员射击成绩的众数及乙队员射击成绩的中位数.
若在甲、乙两名队员中派一名成绩相对稳定的队员参赛,你会选择哪名队员参赛?说明理由.
参考答案
人教版八年级数学下册同步练习第20章《数据的分析》
一、
选择题
1.
【答案】
C
【解答】
解:∵
数据的平均数是,
∴
,
解得:.
把这些数从小到大排列为:,,,,,最中间的数是.
∴
这组数据的中位数是.
故选.
2.
【答案】
C
【解答】
解:,原极差为,现极差为,
极差发生变化,故此选项不正确;
,原平均数为,
现平均数为,
平均数发生变化,故此选项不正确;
,将一组数据为,,,,,,中的一个抄成了,
不影响找第,位的两个数,因此中位数不变,故此选项正确;
,原众数为和,现众数为,
众数发生变化,故此选项不正确.
故选.
3.
【答案】
D
【解答】
解:∵
平均数为,
∴
方差为为
.
故选.
4.
【答案】
B
【解答】
解:这组数据中出现次数最多的是,众数是,选项不符合题意;
∵
,
∴
这组数据的平均数是,
∴
选项符合题意.
,,,,的中位数是,选项不符合题意.
,
∴
这组数据的方差是,
∴
选项不符合题意.
故选
5.
【答案】
C
【解答】
解:∵
,,,,,这六个数的平均数是,
∴
,
解得:.
故选.
6.
【答案】
C
【解答】
解:∵
年龄是岁的有名队员,人数最多,
∴
校舞蹈队队员年龄的众数是.
故选.
7.
【答案】
B
【解答】
解:将这组数据重新排列为
,,,,,,,,,,
所以这组数据的众数为,
中位数为.
故选.
8.
【答案】
B
【解答】
解:∵
甲、乙两种秧苗的平均高度一样,方差分别是和,
∴
,
∴
甲秧苗出苗更整齐.
故选.
9.
【答案】
B
【解答】
解:
只.
故选.
二、
填空题
10.
【答案】
【解答】
解:由平均数的公式得:,
解得,
∴
方差.
故答案为:.
11.
【答案】
【解答】
解:将一这组数据按照从小到大排列后,第五和第六个数均为,
那么由中位数的定义可知,
这组数据的中位数是.
故答案为:.
12.
【答案】
【解答】
解:由每周课外阅读的平均时长为可得,
,
又∵
,
∴
解得
所以众数,中位数,
所以.
故答案为:.
13.
【答案】
【解答】
解:∵
数据,,,,的平均数是,
∴
,
∴
.
∵
数据,,,,的方差是,
∴
,
∴
.
故答案为:.
三、
解答题
14.
【答案】
解:∵
初中组五名同学的成绩为:
,,,,,
∴
成绩的平均数.
∵
该组数据中,出现的次数最多,
∴
众数.
∵
高中组五名同学的成绩为:,,,,,
∴
该组数据中的中位数.
故答案为:,,.
初中代表队决赛成绩的方差是:
?,
∵
,
∴
初中代表队选手成绩较为稳定.
【解答】
解:∵
初中组五名同学的成绩为:
,,,,,
∴
成绩的平均数.
∵
该组数据中,出现的次数最多,
∴
众数.
∵
高中组五名同学的成绩为:,,,,,
∴
该组数据中的中位数.
故答案为:,,.
初中代表队决赛成绩的方差是:
?,
∵
,
∴
初中代表队选手成绩较为稳定.
15.
【答案】
,
经计算,?,,甲、乙平均数相等,
因为,
所以甲的成绩更稳定,
所以甲将被选中.
【解答】
解:甲队员射击的平均成绩是:
?
,
?因为甲、乙两名队员的射击成绩的平均成绩相等,
所以第次的成绩是:
.
故答案为:.
由统计表可知,的次数出现得最多,所以众数是;
将甲运动员射击训练成绩按照从小到大的顺序依次排列,
得,,,,,,,,,,
所以中位数是.
故答案为:;.
经计算,?,,甲、乙平均数相等,
因为,
所以甲的成绩更稳定,
所以甲将被选中.
16.
【答案】
解:(环),
(环).
甲队员射击成绩的众数为环、环;
乙队员射击成绩的中位数为(环).
,
,
因为,,
所以乙的平均数高,成绩相对稳定,选择乙队员参赛.
【解答】
解:(环),
(环).
甲队员射击成绩的众数为环、环;
乙队员射击成绩的中位数为(环).
,
,
因为,,
所以乙的平均数高,成绩相对稳定,选择乙队员参赛.
试卷第4页,总9页
试卷第5页,总9页
第20章《数据的分析》
?
1.
数据的平均数是,则这组数据的中位数是?
?
?
?
A.
B.
C.
D.
2.
一组数据为,,,,,,某同学在抄题的时候,误将其中的一个抄成了,那么该同学所抄的数据和原数据相比,不变的统计量是(?
?
?
?
)
A.极差
B.平均数
C.中位数
D.众数?
3.
数据,,,,的方差是(?
?
?
?
)
A.
B.
C.
D.?
4.
立定跳远是体育中考选考项目之一,体育课上老师记录了某同学的一组立定跳远成绩如表:
则下列关于这组数据的说法,正确的是(?
?
?
?
)
A.众数是
B.平均数是
C.中位数是
D.方差是
5.
,,,,,这六个数的平均数是,则的值为(?
?
?
?
)
A.
B.
C.
D.?
6.
校舞蹈队名队员的年龄情况统计如下表,则校舞蹈队队员年龄的众数是(?
?
?
?
)
年龄(岁)
人数(名)
A.
B.
C.
D.?
7.
某青年球队名队员年龄情况如下:,,,,,,,,,.则这名队员年龄的众数、中位数分别是(????????)
A.,
B.,
C.,
D.,
8.
为了比较甲乙两种水稻秧苗谁出苗更整齐,每种秧苗各随机抽取株,分别量出每株高度,发现甲、乙两种秧苗的平均高度一样,方差分别是和,则下列说法正确的是(?
?
?
?
)
A.甲、乙出苗一样整齐
B.甲秧苗出苗更整齐
C.乙秧苗出苗更整齐
D.无法确定甲、乙出苗谁更整齐
9.
某“中学生暑期环保组”的同学,随机调查了“幸福小区”户家庭一周内使用环保方便袋的数量,数据如下(单位:只):,,,,,,,,,.利用上述数据估计该小区户家庭一周内需要环保方便袋约(?
?
?
?
)
A.只
B.只
C.只
D.只
?
10.
已知一组数据,,,,,它的平均数是,这组数据的方差是________.
?
11.
某校九年级学生参加体育测试,其中人的引体向上成绩如下表:
完成引体向上的个数
人?数
这人完成引体向上个数的中位数是________.?
12.
为调查某班每周课外阅读时长,现抽取其中名同学的阅读时长进行了统计,并整理成下表.
阅读时长/h
15
20
25
30
人数/人
1
x
y
2
若这名同学每周课外阅读的平均时长为,中位数是,众数是,则________.
13.
已知一组数据,,,,的平均数是,方差是,则数据,,,,的方差是________.
?
14.
我市某中学举行“校园好声音”歌手大赛,初、高中根据初赛成绩各选出名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的名选手的决赛成绩(满分)如图所示:
根据图示信息,整理分析数据如表:
平均数(分)
中位数(分)
众数(分)
初中部
高中部
求出表格中,,;
小明同学已经算出高中代表队决赛成绩的方差是,请你计算出初中代表队决赛成绩的方差,并判断哪一个代表队选手成绩较为稳定.
?
15.
某校要从甲、乙两名队员中选派一人参加射击比赛,甲、乙两名队员在相同的条件下各射击次,每次命中的环数如下表所示.
次数
①
②
③
④
⑤
⑥
⑦
⑧
⑨
⑩
甲成绩(环数)
乙成绩(环数)
已知甲、乙两名队员的射击成绩的平均成绩相等,请补齐乙的成绩.
甲运动员射击训练成绩的众数是________,中位数是________.
求甲、乙两名队员的射击成绩的方差分别是多少?根据计算结果,从平均数和方差的角度分析,谁将被选中.
?
16.
甲、乙两名队员在相同的条件下各射击次,他们的射击成绩(单位:环)如图所示.
分别求甲、乙两名队员射击成绩的平均数.
直接写出甲队员射击成绩的众数及乙队员射击成绩的中位数.
若在甲、乙两名队员中派一名成绩相对稳定的队员参赛,你会选择哪名队员参赛?说明理由.
参考答案
人教版八年级数学下册同步练习第20章《数据的分析》
一、
选择题
1.
【答案】
C
【解答】
解:∵
数据的平均数是,
∴
,
解得:.
把这些数从小到大排列为:,,,,,最中间的数是.
∴
这组数据的中位数是.
故选.
2.
【答案】
C
【解答】
解:,原极差为,现极差为,
极差发生变化,故此选项不正确;
,原平均数为,
现平均数为,
平均数发生变化,故此选项不正确;
,将一组数据为,,,,,,中的一个抄成了,
不影响找第,位的两个数,因此中位数不变,故此选项正确;
,原众数为和,现众数为,
众数发生变化,故此选项不正确.
故选.
3.
【答案】
D
【解答】
解:∵
平均数为,
∴
方差为为
.
故选.
4.
【答案】
B
【解答】
解:这组数据中出现次数最多的是,众数是,选项不符合题意;
∵
,
∴
这组数据的平均数是,
∴
选项符合题意.
,,,,的中位数是,选项不符合题意.
,
∴
这组数据的方差是,
∴
选项不符合题意.
故选
5.
【答案】
C
【解答】
解:∵
,,,,,这六个数的平均数是,
∴
,
解得:.
故选.
6.
【答案】
C
【解答】
解:∵
年龄是岁的有名队员,人数最多,
∴
校舞蹈队队员年龄的众数是.
故选.
7.
【答案】
B
【解答】
解:将这组数据重新排列为
,,,,,,,,,,
所以这组数据的众数为,
中位数为.
故选.
8.
【答案】
B
【解答】
解:∵
甲、乙两种秧苗的平均高度一样,方差分别是和,
∴
,
∴
甲秧苗出苗更整齐.
故选.
9.
【答案】
B
【解答】
解:
只.
故选.
二、
填空题
10.
【答案】
【解答】
解:由平均数的公式得:,
解得,
∴
方差.
故答案为:.
11.
【答案】
【解答】
解:将一这组数据按照从小到大排列后,第五和第六个数均为,
那么由中位数的定义可知,
这组数据的中位数是.
故答案为:.
12.
【答案】
【解答】
解:由每周课外阅读的平均时长为可得,
,
又∵
,
∴
解得
所以众数,中位数,
所以.
故答案为:.
13.
【答案】
【解答】
解:∵
数据,,,,的平均数是,
∴
,
∴
.
∵
数据,,,,的方差是,
∴
,
∴
.
故答案为:.
三、
解答题
14.
【答案】
解:∵
初中组五名同学的成绩为:
,,,,,
∴
成绩的平均数.
∵
该组数据中,出现的次数最多,
∴
众数.
∵
高中组五名同学的成绩为:,,,,,
∴
该组数据中的中位数.
故答案为:,,.
初中代表队决赛成绩的方差是:
?,
∵
,
∴
初中代表队选手成绩较为稳定.
【解答】
解:∵
初中组五名同学的成绩为:
,,,,,
∴
成绩的平均数.
∵
该组数据中,出现的次数最多,
∴
众数.
∵
高中组五名同学的成绩为:,,,,,
∴
该组数据中的中位数.
故答案为:,,.
初中代表队决赛成绩的方差是:
?,
∵
,
∴
初中代表队选手成绩较为稳定.
15.
【答案】
,
经计算,?,,甲、乙平均数相等,
因为,
所以甲的成绩更稳定,
所以甲将被选中.
【解答】
解:甲队员射击的平均成绩是:
?
,
?因为甲、乙两名队员的射击成绩的平均成绩相等,
所以第次的成绩是:
.
故答案为:.
由统计表可知,的次数出现得最多,所以众数是;
将甲运动员射击训练成绩按照从小到大的顺序依次排列,
得,,,,,,,,,,
所以中位数是.
故答案为:;.
经计算,?,,甲、乙平均数相等,
因为,
所以甲的成绩更稳定,
所以甲将被选中.
16.
【答案】
解:(环),
(环).
甲队员射击成绩的众数为环、环;
乙队员射击成绩的中位数为(环).
,
,
因为,,
所以乙的平均数高,成绩相对稳定,选择乙队员参赛.
【解答】
解:(环),
(环).
甲队员射击成绩的众数为环、环;
乙队员射击成绩的中位数为(环).
,
,
因为,,
所以乙的平均数高,成绩相对稳定,选择乙队员参赛.
试卷第4页,总9页
试卷第5页,总9页
