2020——2021学年度 北师大版数学八年级下册 第三章 图形的平移与旋转 全章练习(Word版 含答案)
文档属性
| 名称 | 2020——2021学年度 北师大版数学八年级下册 第三章 图形的平移与旋转 全章练习(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 234.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-12 11:49:24 | ||
图片预览


文档简介
第三章 图形的平移与旋转
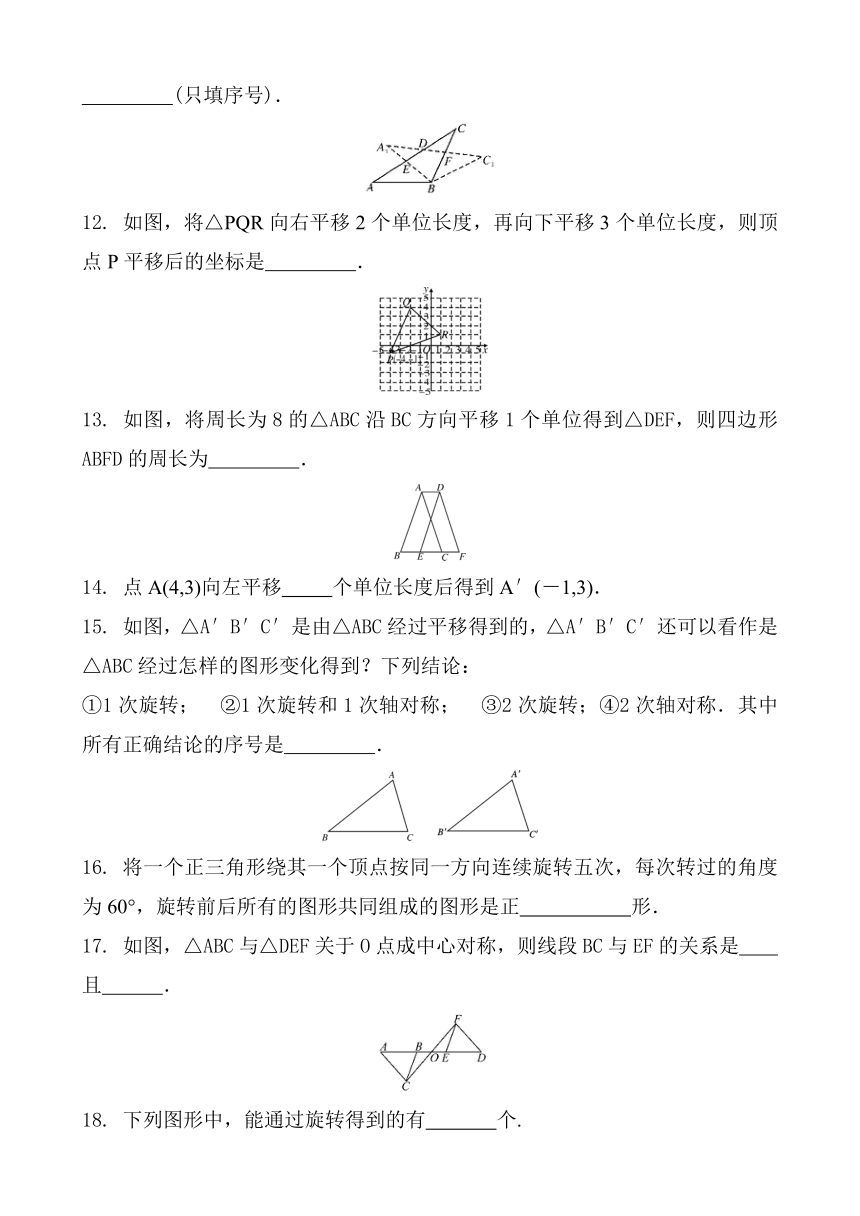
1.下列图案中,是中心对称图形但不是轴对称图形的是( )
2. 下列图形中可由其中的部分图形经过平移得到的是( )
3. 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=25°,则∠BAA′的度数是( )
A.55° B.60° C.65° D.70°
4.如图所示,在Rt△ABC中,BC是斜边,P是三角形内一点,将△ABP绕点A逆时针旋转后,能与△ACP′重合,如果AP=3,则PP′的长为( )
A. B.3 C.2 D.3
5.如图,已知正方形ABCD的边长为3,点E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.若AE=1,则FM的长为( )
A.2 B.2 C.3 D.
6. 如图,将△ABC绕点B顺时针旋转60°得到△DBE,点C的对应点E恰好落在AB的延长线上,连接AD,下列结论一定正确的是( )
A.∠ABD=∠E B.∠CBE=∠C C.AD∥BC D.AD=BC
7. 下列图形中,能由左图经过一次平移得到的图形是( )
8. 已知某一运动方式为:先竖直向上运动1个单位长度后,再水平向左运动2个单位长度,现有一动点P第一次从原点O出发,按运动方式运动到P1,第2次从点P1出发按运动方式运动到点P2,则此时点P2的坐标是( )
A.(4,2) B.(-4,2) C.(-4,-2) D.(4,-2)
9. 如图,将△ABC绕点C顺时针旋转90°得到△EDC,若点A、D、E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )
A.65° B.70° C.75° D.80°
10. 在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点
A2n+1的坐标是( )
A.(4n-1,) B.(2n-1,) C.(4n+1,) D.(2n+1,)
11. 如图,在△ABC中,AB=BC,将△ABC绕点B顺时针旋转a度,得到△A1BC1,A1B交AC于点E,A1C1分别交AC,BC于点D,F,下列结论:①∠CDF=a度;②A1E=CF;③DF=FC;④BE=BF.其中正确的有
(只填序号).
12. 如图,将△PQR向右平移2个单位长度,再向下平移3个单位长度,则顶点P平移后的坐标是 .
13. 如图,将周长为8的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为 .
14. 点A(4,3)向左平移 个单位长度后得到A′(-1,3).
15. 如图,△A′B′C′是由△ABC经过平移得到的,△A′B′C′还可以看作是△ABC经过怎样的图形变化得到?下列结论:
①1次旋转; ②1次旋转和1次轴对称; ③2次旋转;④2次轴对称.其中所有正确结论的序号是 .
16. 将一个正三角形绕其一个顶点按同一方向连续旋转五次,每次转过的角度为60°,旋转前后所有的图形共同组成的图形是正 形.
17. 如图,△ABC与△DEF关于O点成中心对称,则线段BC与EF的关系是
且 .
18. 下列图形中,能通过旋转得到的有 个.
19. 如图所示,若A、B、C分别为三个圆的圆心,且圆的半径都是2cm,则圆B可看做是圆A沿水平方向平移 cm得到的;圆C可看做圆A沿着与水平方向成 °角的方向平移 cm得到的,点C到AB的距离是 cm.
20. 如图,△ABC、△BDE都是等腰直角三角形,BA=BC,BD=BE,AC=4,DE=2,将△BDE绕点B逆时针方向旋转后得△BD′E′,当点E′恰好落在线段AD′上时,求CE′的长.
21. 如图,在等腰Rt△ABC中,∠ACB=90°,AB=14,点D,E分别在边AB,BC上,将线段ED绕点E按逆时针方向旋转90°得到EF.如图,若AD=BD,点E与点C重合,AF与DC相交于点O,求证:BD=2DO.
22. 如图,△ABC是等边三角形,将△ABC沿直线BC向右平移,使B点与C点重合,得到△DCE,连接BD,交AC于点F.猜想AC与BD的位置关系,并证明你的结论.
23. 如图,点P是等边△ABC内一点,PA=4,PB=3,PC=5,线段AP绕点A逆时针旋转60°得到线段AQ,连接PQ.
(1)求PQ的长;
(2)求∠APB的度数.
答案;
1---10 CACBD CCBAC
11. ① ② ④
12. (-2,-4)
13. 10
14. 5
15. ② ④
16. 六边
17. 平行 相等
18. 4
19. 4 60 4 2
20. 解:如图,
连接CE′,∵△ABC、△BDE都是等腰直角三角形,BA=BC,BD=BE,AC=4,DE=2,∴AB=BC=2,BD=BE=2,∵将△BDE绕点B逆时针方向旋转后得△BD′E′,∴D′B=BE′=BD=2,∠D′BE′=90°,∠D′BD=∠ABE′,∴∠ABD′=∠CBE′,∴△ABD′≌△CBE′(SAS),∴∠D′=∠CE′B=45°,过B作BH⊥CE′于H,在Rt△BHE′中,BH=E′H=BE′=,
在Rt△BCH中,CH==,∴CE′=+.
21. 解:由旋转的性质得:CD=CF,∠DCF=90°,∵△ABC是等腰直角三角形,AD=BD,∴∠ADO=90°,CD=BD=AD,∴∠DCF=∠ADC,在△ADO和△FCO中,∵,∴△ADO≌△FCO(AAS),∴DO=CO,∴BD=CD=2DO.
22. 解:垂直.证明:∵△DCE由△ABC平移而来,∴△DCE≌△ABC, ∴△DCE是等边三角形,∴BC=CD,∠ACB=∠DCE=60°,∴∠ACD=180°-120°=60°,∴∠ACD=∠ACB,∵BC=CD,∴AC⊥BD.
23. 解:(1)∵AP=AQ,∠PAQ=60°,∴△APQ是等边三角形,∴PQ=PA=4;
(2)连接QC,∵△ABC,△APQ都是等边三角形,∴∠BAC=∠PAQ=60°,
∴∠BAP=∠CAQ=60°-∠PAC,在△ABP和△ACQ中,,∴△ABP≌△ACQ(SAS),∴BP=CQ=3,∠APB=∠AQC,
∵在△PQC中,PQ2+CQ2=PC2,∴△PQC是直角三角形,且∠PQC=90°,
∵△APQ是等边三角形,∴∠AQP=60°,∴∠APB=∠AQC=60°+90°=150°.
1.下列图案中,是中心对称图形但不是轴对称图形的是( )
2. 下列图形中可由其中的部分图形经过平移得到的是( )
3. 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=25°,则∠BAA′的度数是( )
A.55° B.60° C.65° D.70°
4.如图所示,在Rt△ABC中,BC是斜边,P是三角形内一点,将△ABP绕点A逆时针旋转后,能与△ACP′重合,如果AP=3,则PP′的长为( )
A. B.3 C.2 D.3
5.如图,已知正方形ABCD的边长为3,点E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.若AE=1,则FM的长为( )
A.2 B.2 C.3 D.
6. 如图,将△ABC绕点B顺时针旋转60°得到△DBE,点C的对应点E恰好落在AB的延长线上,连接AD,下列结论一定正确的是( )
A.∠ABD=∠E B.∠CBE=∠C C.AD∥BC D.AD=BC
7. 下列图形中,能由左图经过一次平移得到的图形是( )
8. 已知某一运动方式为:先竖直向上运动1个单位长度后,再水平向左运动2个单位长度,现有一动点P第一次从原点O出发,按运动方式运动到P1,第2次从点P1出发按运动方式运动到点P2,则此时点P2的坐标是( )
A.(4,2) B.(-4,2) C.(-4,-2) D.(4,-2)
9. 如图,将△ABC绕点C顺时针旋转90°得到△EDC,若点A、D、E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )
A.65° B.70° C.75° D.80°
10. 在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点
A2n+1的坐标是( )
A.(4n-1,) B.(2n-1,) C.(4n+1,) D.(2n+1,)
11. 如图,在△ABC中,AB=BC,将△ABC绕点B顺时针旋转a度,得到△A1BC1,A1B交AC于点E,A1C1分别交AC,BC于点D,F,下列结论:①∠CDF=a度;②A1E=CF;③DF=FC;④BE=BF.其中正确的有
(只填序号).
12. 如图,将△PQR向右平移2个单位长度,再向下平移3个单位长度,则顶点P平移后的坐标是 .
13. 如图,将周长为8的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为 .
14. 点A(4,3)向左平移 个单位长度后得到A′(-1,3).
15. 如图,△A′B′C′是由△ABC经过平移得到的,△A′B′C′还可以看作是△ABC经过怎样的图形变化得到?下列结论:
①1次旋转; ②1次旋转和1次轴对称; ③2次旋转;④2次轴对称.其中所有正确结论的序号是 .
16. 将一个正三角形绕其一个顶点按同一方向连续旋转五次,每次转过的角度为60°,旋转前后所有的图形共同组成的图形是正 形.
17. 如图,△ABC与△DEF关于O点成中心对称,则线段BC与EF的关系是
且 .
18. 下列图形中,能通过旋转得到的有 个.
19. 如图所示,若A、B、C分别为三个圆的圆心,且圆的半径都是2cm,则圆B可看做是圆A沿水平方向平移 cm得到的;圆C可看做圆A沿着与水平方向成 °角的方向平移 cm得到的,点C到AB的距离是 cm.
20. 如图,△ABC、△BDE都是等腰直角三角形,BA=BC,BD=BE,AC=4,DE=2,将△BDE绕点B逆时针方向旋转后得△BD′E′,当点E′恰好落在线段AD′上时,求CE′的长.
21. 如图,在等腰Rt△ABC中,∠ACB=90°,AB=14,点D,E分别在边AB,BC上,将线段ED绕点E按逆时针方向旋转90°得到EF.如图,若AD=BD,点E与点C重合,AF与DC相交于点O,求证:BD=2DO.
22. 如图,△ABC是等边三角形,将△ABC沿直线BC向右平移,使B点与C点重合,得到△DCE,连接BD,交AC于点F.猜想AC与BD的位置关系,并证明你的结论.
23. 如图,点P是等边△ABC内一点,PA=4,PB=3,PC=5,线段AP绕点A逆时针旋转60°得到线段AQ,连接PQ.
(1)求PQ的长;
(2)求∠APB的度数.
答案;
1---10 CACBD CCBAC
11. ① ② ④
12. (-2,-4)
13. 10
14. 5
15. ② ④
16. 六边
17. 平行 相等
18. 4
19. 4 60 4 2
20. 解:如图,
连接CE′,∵△ABC、△BDE都是等腰直角三角形,BA=BC,BD=BE,AC=4,DE=2,∴AB=BC=2,BD=BE=2,∵将△BDE绕点B逆时针方向旋转后得△BD′E′,∴D′B=BE′=BD=2,∠D′BE′=90°,∠D′BD=∠ABE′,∴∠ABD′=∠CBE′,∴△ABD′≌△CBE′(SAS),∴∠D′=∠CE′B=45°,过B作BH⊥CE′于H,在Rt△BHE′中,BH=E′H=BE′=,
在Rt△BCH中,CH==,∴CE′=+.
21. 解:由旋转的性质得:CD=CF,∠DCF=90°,∵△ABC是等腰直角三角形,AD=BD,∴∠ADO=90°,CD=BD=AD,∴∠DCF=∠ADC,在△ADO和△FCO中,∵,∴△ADO≌△FCO(AAS),∴DO=CO,∴BD=CD=2DO.
22. 解:垂直.证明:∵△DCE由△ABC平移而来,∴△DCE≌△ABC, ∴△DCE是等边三角形,∴BC=CD,∠ACB=∠DCE=60°,∴∠ACD=180°-120°=60°,∴∠ACD=∠ACB,∵BC=CD,∴AC⊥BD.
23. 解:(1)∵AP=AQ,∠PAQ=60°,∴△APQ是等边三角形,∴PQ=PA=4;
(2)连接QC,∵△ABC,△APQ都是等边三角形,∴∠BAC=∠PAQ=60°,
∴∠BAP=∠CAQ=60°-∠PAC,在△ABP和△ACQ中,,∴△ABP≌△ACQ(SAS),∴BP=CQ=3,∠APB=∠AQC,
∵在△PQC中,PQ2+CQ2=PC2,∴△PQC是直角三角形,且∠PQC=90°,
∵△APQ是等边三角形,∴∠AQP=60°,∴∠APB=∠AQC=60°+90°=150°.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
