2021年浙教版八年级上册数学期末压轴题例析(Word版含答案)
文档属性
| 名称 | 2021年浙教版八年级上册数学期末压轴题例析(Word版含答案) | 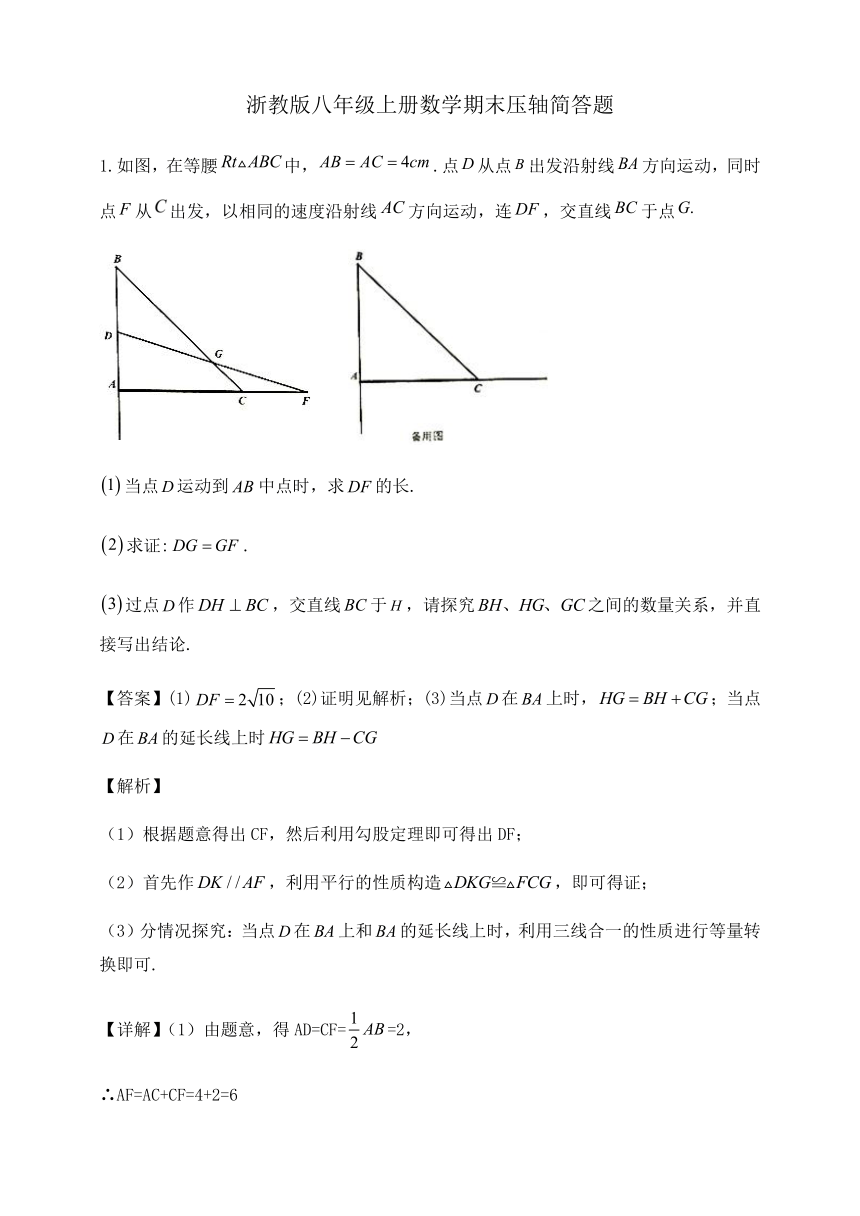 | |
| 格式 | docx | ||
| 文件大小 | 862.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-12 11:51:10 | ||
图片预览

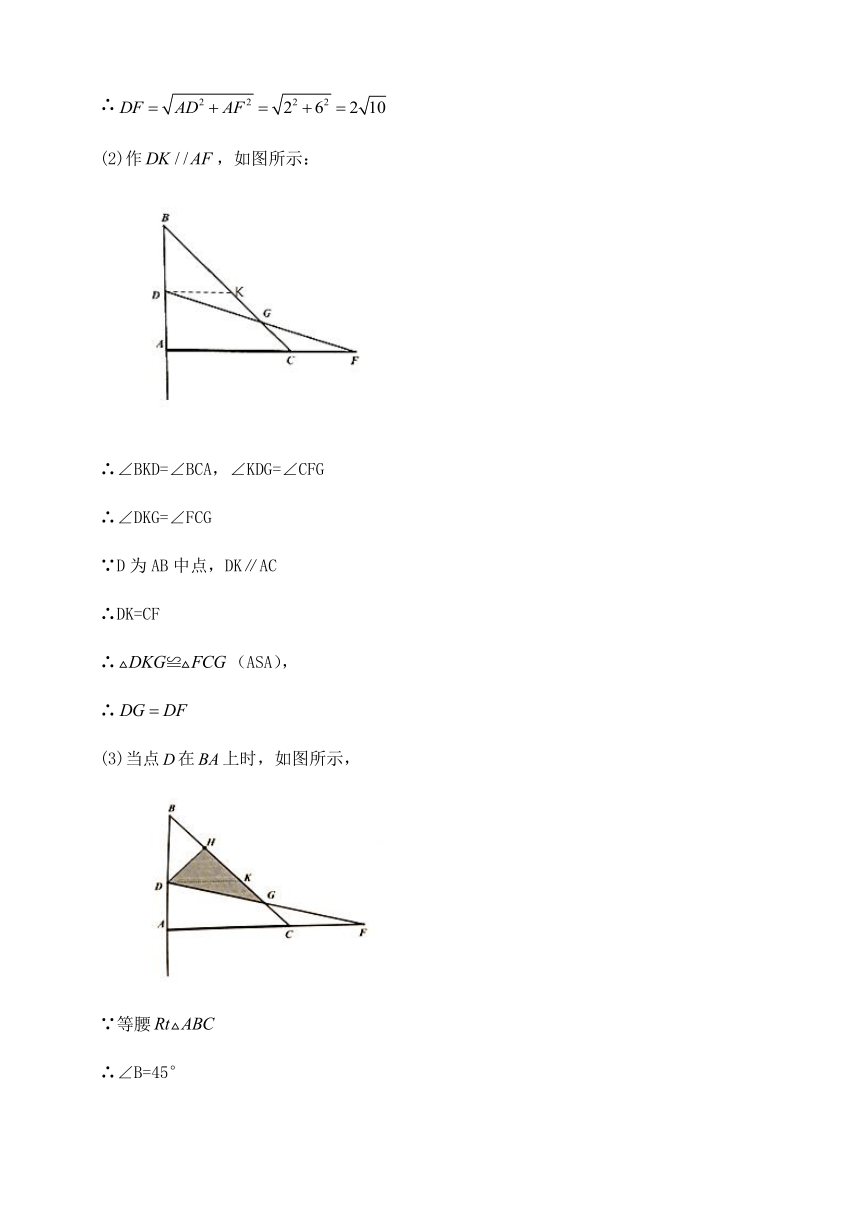



文档简介
浙教版八年级上册数学期末压轴简答题
1.如图,在等腰false中,false.点false从点false出发沿射线false方向运动,同时点false从出发,以相同的速度沿射线false方向运动,连false,交直线false于点false
false当点false运动到false中点时,求false的长.
false求证:false.
false过点false作false,交直线false于false,请探究false之间的数量关系,并直接写出结论.
【答案】(1)false;(2)证明见解析;(3)当点false在false上时,false;当点false在false的延长线上时false
【解析】
(1)根据题意得出CF,然后利用勾股定理即可得出DF;
(2)首先作false,利用平行的性质构造false,即可得证;
(3)分情况探究:当点false在false上和false的延长线上时,利用三线合一的性质进行等量转换即可.
【详解】(1)由题意,得AD=CF=false=2,
∴AF=AC+CF=4+2=6
∴false
(2)作false,如图所示:
∴∠BKD=∠BCA,∠KDG=∠CFG
∴∠DKG=∠FCG
∵D为AB中点,DK∥AC
∴DK=CF
∴false(ASA),
∴false
(3)当点false在false上时,如图所示,
∵等腰false
∴∠B=45°
∵false
∴BH=HK
∵false
∴KG=CG
∴false;
当点false在false的延长线上时,如图所示:
∵等腰false
∴∠B=45°
∵false
∴BH=GH
∴false
2.我们定义:如果两个等腰三角形的顶角相等,且项角的顶点互相重合,则称此图形为“手拉手全等模型”.因为顶点相连的四条边,形象的可以看作两双手,所以通常称为“手拉手模型”.例如,如(1),false与false都是等腰三角形,其中false,则△ABD≌△ACE(SAS).
(1)熟悉模型:如(2),已知false与false都是等腰三角形,AB=AC,AD=AE,且false,求证:false;
(2)运用模型:如(3),false为等边false内一点,且false,求false的度数.小明在解决此问题时,根据前面的“手拉手全等模型”,以false为边构造等边false,这样就有两个等边三角形共顶点false,然后连结false,通过转化的思想求出了false的度数,则false的度数为 度;
(3)深化模型:如(4),在四边形false中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,求false的长.
【答案】(1)见解析;(2)150°;(3)false
【详解】(1)∵false,
∴false,
在△ABD和△ACE中,
∵false,
false,
AD=AE,
∴△ABD≌△ACE,
∴false;
(2)由小明的构造方法可得,
BP=BM=PM,∠PBM=∠PMB=60°,
∴∠ABP=∠CBM,
又∵AB=BC,
∴△BAP≌△BMC,
∴∠BPA=∠BMC,AP=CM,
∵false,
∴false,
设CM=3x,PM=4x,PC=5x,
∵(5x)2=(3x)2+(4x)2,
∴PC2=CM2+PM2,
∴△PCM是直角三角形,
∴∠PMC=90°,
∴∠BPA=∠BMC=60°+90°=150°;
(3)∵∠ACB=∠ABC=45°,
∴∠BAC=90°,且AC=AB.
将△ADB绕点A顺时针旋转90°,得到△ACE,
∴AD=AE,∠DAE=90°,BD=CE.
∴∠EDA=45°,DE=falseAD=4false.
∵∠ADC=45°,
∴∠EDC=45°+45°=90°.
在Rt△DCE中,利用勾股定理可得,
CE= false,
∴BD=CE=false.
3.已知,一次函数false图像与false轴、false轴分别交于点A、点B,与直线false 相交于点C,过点B作false轴的平行线l.点P是直线l上的一个动点.
(1)求点A,点B的坐标.
(2)若false,求点P的坐标.
(3)若点E是直线false上的一个动点,当△APE是以AP为直角边的等腰直角三角形时,求点E的坐标.
【答案】(1)false,false;(2)false或者false;(3)false点坐标为:false或false或false或false.
【详解】解:(1)当x=0时,y=6;当y=0时,x=8,
∴false,false;
(2)联立false
解得:false,
∴为false.
∴false.
∴false,
解得:false.
∴false或false.
(3)若△APE是以AP为直角边的等腰直角三角形,则有AP=PE,false,设点E坐标为E(x,false),A(8,0),
∵false或false
∴当false时,有
false
化简求解即可,同理可得出当false时,点E的坐标,
综上所述,false点坐标为:false或false或false或false.
4.已知关于x的一次函数false的图象与x轴,y轴分别交于A,B两点,过点B作直线false的垂线,垂足为M,连结AM.
(1)求点A的坐标;
(2)当false为直角三角形时,求点M的坐标;
(3)求false的面积false用含m的代数式表示,写出m相应的取值范围false.
解:false当false时,false,
解得,false,
false点A的坐标为false;
false为直角三角形时,false,false,
false,
false直线false,
false直线false直线false,
false,
则false,
false,
false,
false,
作false于H,
则false,
false点M的坐标为false;
false直线false与y轴的夹角是false,
false,
false,
则false的面积false的面积false的面积false的面积
false,
false.
5.如图1,在三角形false中,把false绕点false顺时针旋转false得到false,把false绕点false逆时针旋转false,得到false,连接false,过点false作false的垂线,交false于点false,交false于点false.
【特例尝试】如图2,当false时,
①求证:false;
②猜想false与false的数量关系并说明理由.
【理想论证】在图1中,当false为任意三角形时,②中false与false的数量关系还成立吗?请给予证明.
【拓展应用】如图3,直线false与false轴,false轴分别交于false、false两点,分别以false,false为直角边在第二、一象限内作等腰false和等腰false,连接false,交false轴于点false.试猜想false的长是否为定值,若是,请求出这个值;若不是,请说明理由.
【答案】[特例尝试]①见解析,②false,理由见解析;[理想论证]成立,证明见解析;[拓展应用]是定值,false.
详解】[特例尝试]①证明:∵BA⊥AD,AC⊥AE
∴∠BAD=∠CAE=90°,
又∵false
∴false
②false,证明如下:
由旋转的性质可得AD=AB,AE=AC,
又∵false,
∴△BAC≌△DAE(SAS)
∴∠EDA=∠CBA,∠DEA=∠BCA,BC=DE,
∵GF⊥BC,false
∴∠CAF+∠ACB=90°,∠ABC+∠ACB=90°
∴∠ABC=∠CAF=∠DAG=∠EDA,
∴DG=AG,
同理可证GE=AG,
∴false.
[理想论证]成立,理由如下:
过点false作false,交false延长线于点false,过点false做false,交false于点false.
∵false
∴falsefalse
∵false
∴false
∴false
∵false
∴false
∴false,false
同理可得false,false
∴false
∵false
∴false
∴false
∵false
∴false
[拓展应用]对于一次函数false,当y=0时,即false,
解得false,
∴false,
由题[理想论证]可知false.
6.证明.如果两个三角形有两条边和其中一边上的中线分别相等,那么这两个三角形全等,
(1)小玲在思考这道题时.画出图形,写出已知和求证.
已知:在false和false中,false,false,false是false边false上的中线,false是false边false上的中线,false.
求证:false.
请你帮她完成证明过程.
(2)小玲接着提出了两个猜想:
①如果两个三角形有两条边和第三边上的中线分别相等,那么这两个三角形全等;
②如果两个三角形有两条边和第三边上的高分别相等,那么这两个三角形全等;
请你分别判断这两个猜想是否正确,如果正确,请予以证明,如果不正确,请举出反例.
【答案】(1)见解析;(2)命题①正确,证明见解析;命题②不正确,反例见解析
【详解】(1)∵false是false边上的中线,
∴false,同理false,
∵false,∴false,
∵false,false,
∴false,
∴false,
∵false,false,
∴false;
(2)命题①正确,已知如图1、图2,
在false和false中,false,false,false是false边false上的中线,false是false边false上的中线,且false.
求证:false.
证明:延长false到false,使false,连接false,延长false到false,使false,连接false.
∵false是false边false上的中线,
∴BD=DC,
∵false
∴false(SAS),
∴false,false,
同理:false,false,
∵false,false.
∵false,false,false,
∴false,false,
∴false,
∴false,false,
∴false,
∴false,即false,
∵false,false,
∴false;
命题②不正确,如图3、图4,
在false和false中,false,false,false边上的高线为false,false边上的高线为false,false,false与false不全等.
7.如图,直线false分别与false轴,false轴交于点false,false,过点false的直线false交false轴于点.false为false的中点,false为射线false上一动点,连结false,false,过false作false于点false.
(1)直接写出点false,false的坐标:false(______,______),false(______,______);
(2)当false为false中点时,求false的长;
(3)当false是以false为腰的等腰三角形时,求点false坐标;
(4)当点false在线段false(不与false,重合)上运动时,作false关于false的对称点false,若false落在false轴上,则false的长为_______.
【答案】(1)-2,0;2,0;(2)false;(3)当false或false时,false是以false为腰的等腰三角形;(4)false.
【解】令y=0,得x=-2,
∴false,
令x=0,得y=4,∴B(0,4)
把B(0,4)代入false,求得b=4,
∴直线BC的解析式为false
令y=0,得x=4,∴false
∵false为false的中点
∴false
故答案为:-2,0;2,0;
(2)由(1)得B(0,4),false
当false为false的中点时,则false,
∵false为false的中点,
∴false轴,
false,false,
∴false
∵false,
∴false
(3)∵点false是射线false上一动点,设false,当false是以false为腰的等腰三角形时,
①若false,false,解得:false,false(舍去),此时false;
②若false,false,解得:false,此时false.
综上,当false或false时,false是以false为腰的等腰三角形.
(4)∵false关于false的对称点false,若false落在false轴上
∴点false为A点,
∴AD=PD=4,
设false,作PF⊥AC于F点,
∴DF=2-x,PF=-x+4,
在Rt△PFD中,DF2+PF2=DP2
即(2-x)2+(-x+4)2=42
解得x=3-false(3+false舍去)
∴P(3-false,false+1),
∴false=false=false
故答案为:false.
1.如图,在等腰false中,false.点false从点false出发沿射线false方向运动,同时点false从出发,以相同的速度沿射线false方向运动,连false,交直线false于点false
false当点false运动到false中点时,求false的长.
false求证:false.
false过点false作false,交直线false于false,请探究false之间的数量关系,并直接写出结论.
【答案】(1)false;(2)证明见解析;(3)当点false在false上时,false;当点false在false的延长线上时false
【解析】
(1)根据题意得出CF,然后利用勾股定理即可得出DF;
(2)首先作false,利用平行的性质构造false,即可得证;
(3)分情况探究:当点false在false上和false的延长线上时,利用三线合一的性质进行等量转换即可.
【详解】(1)由题意,得AD=CF=false=2,
∴AF=AC+CF=4+2=6
∴false
(2)作false,如图所示:
∴∠BKD=∠BCA,∠KDG=∠CFG
∴∠DKG=∠FCG
∵D为AB中点,DK∥AC
∴DK=CF
∴false(ASA),
∴false
(3)当点false在false上时,如图所示,
∵等腰false
∴∠B=45°
∵false
∴BH=HK
∵false
∴KG=CG
∴false;
当点false在false的延长线上时,如图所示:
∵等腰false
∴∠B=45°
∵false
∴BH=GH
∴false
2.我们定义:如果两个等腰三角形的顶角相等,且项角的顶点互相重合,则称此图形为“手拉手全等模型”.因为顶点相连的四条边,形象的可以看作两双手,所以通常称为“手拉手模型”.例如,如(1),false与false都是等腰三角形,其中false,则△ABD≌△ACE(SAS).
(1)熟悉模型:如(2),已知false与false都是等腰三角形,AB=AC,AD=AE,且false,求证:false;
(2)运用模型:如(3),false为等边false内一点,且false,求false的度数.小明在解决此问题时,根据前面的“手拉手全等模型”,以false为边构造等边false,这样就有两个等边三角形共顶点false,然后连结false,通过转化的思想求出了false的度数,则false的度数为 度;
(3)深化模型:如(4),在四边形false中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,求false的长.
【答案】(1)见解析;(2)150°;(3)false
【详解】(1)∵false,
∴false,
在△ABD和△ACE中,
∵false,
false,
AD=AE,
∴△ABD≌△ACE,
∴false;
(2)由小明的构造方法可得,
BP=BM=PM,∠PBM=∠PMB=60°,
∴∠ABP=∠CBM,
又∵AB=BC,
∴△BAP≌△BMC,
∴∠BPA=∠BMC,AP=CM,
∵false,
∴false,
设CM=3x,PM=4x,PC=5x,
∵(5x)2=(3x)2+(4x)2,
∴PC2=CM2+PM2,
∴△PCM是直角三角形,
∴∠PMC=90°,
∴∠BPA=∠BMC=60°+90°=150°;
(3)∵∠ACB=∠ABC=45°,
∴∠BAC=90°,且AC=AB.
将△ADB绕点A顺时针旋转90°,得到△ACE,
∴AD=AE,∠DAE=90°,BD=CE.
∴∠EDA=45°,DE=falseAD=4false.
∵∠ADC=45°,
∴∠EDC=45°+45°=90°.
在Rt△DCE中,利用勾股定理可得,
CE= false,
∴BD=CE=false.
3.已知,一次函数false图像与false轴、false轴分别交于点A、点B,与直线false 相交于点C,过点B作false轴的平行线l.点P是直线l上的一个动点.
(1)求点A,点B的坐标.
(2)若false,求点P的坐标.
(3)若点E是直线false上的一个动点,当△APE是以AP为直角边的等腰直角三角形时,求点E的坐标.
【答案】(1)false,false;(2)false或者false;(3)false点坐标为:false或false或false或false.
【详解】解:(1)当x=0时,y=6;当y=0时,x=8,
∴false,false;
(2)联立false
解得:false,
∴为false.
∴false.
∴false,
解得:false.
∴false或false.
(3)若△APE是以AP为直角边的等腰直角三角形,则有AP=PE,false,设点E坐标为E(x,false),A(8,0),
∵false或false
∴当false时,有
false
化简求解即可,同理可得出当false时,点E的坐标,
综上所述,false点坐标为:false或false或false或false.
4.已知关于x的一次函数false的图象与x轴,y轴分别交于A,B两点,过点B作直线false的垂线,垂足为M,连结AM.
(1)求点A的坐标;
(2)当false为直角三角形时,求点M的坐标;
(3)求false的面积false用含m的代数式表示,写出m相应的取值范围false.
解:false当false时,false,
解得,false,
false点A的坐标为false;
false为直角三角形时,false,false,
false,
false直线false,
false直线false直线false,
false,
则false,
false,
false,
false,
作false于H,
则false,
false点M的坐标为false;
false直线false与y轴的夹角是false,
false,
false,
则false的面积false的面积false的面积false的面积
false,
false.
5.如图1,在三角形false中,把false绕点false顺时针旋转false得到false,把false绕点false逆时针旋转false,得到false,连接false,过点false作false的垂线,交false于点false,交false于点false.
【特例尝试】如图2,当false时,
①求证:false;
②猜想false与false的数量关系并说明理由.
【理想论证】在图1中,当false为任意三角形时,②中false与false的数量关系还成立吗?请给予证明.
【拓展应用】如图3,直线false与false轴,false轴分别交于false、false两点,分别以false,false为直角边在第二、一象限内作等腰false和等腰false,连接false,交false轴于点false.试猜想false的长是否为定值,若是,请求出这个值;若不是,请说明理由.
【答案】[特例尝试]①见解析,②false,理由见解析;[理想论证]成立,证明见解析;[拓展应用]是定值,false.
详解】[特例尝试]①证明:∵BA⊥AD,AC⊥AE
∴∠BAD=∠CAE=90°,
又∵false
∴false
②false,证明如下:
由旋转的性质可得AD=AB,AE=AC,
又∵false,
∴△BAC≌△DAE(SAS)
∴∠EDA=∠CBA,∠DEA=∠BCA,BC=DE,
∵GF⊥BC,false
∴∠CAF+∠ACB=90°,∠ABC+∠ACB=90°
∴∠ABC=∠CAF=∠DAG=∠EDA,
∴DG=AG,
同理可证GE=AG,
∴false.
[理想论证]成立,理由如下:
过点false作false,交false延长线于点false,过点false做false,交false于点false.
∵false
∴falsefalse
∵false
∴false
∴false
∵false
∴false
∴false,false
同理可得false,false
∴false
∵false
∴false
∴false
∵false
∴false
[拓展应用]对于一次函数false,当y=0时,即false,
解得false,
∴false,
由题[理想论证]可知false.
6.证明.如果两个三角形有两条边和其中一边上的中线分别相等,那么这两个三角形全等,
(1)小玲在思考这道题时.画出图形,写出已知和求证.
已知:在false和false中,false,false,false是false边false上的中线,false是false边false上的中线,false.
求证:false.
请你帮她完成证明过程.
(2)小玲接着提出了两个猜想:
①如果两个三角形有两条边和第三边上的中线分别相等,那么这两个三角形全等;
②如果两个三角形有两条边和第三边上的高分别相等,那么这两个三角形全等;
请你分别判断这两个猜想是否正确,如果正确,请予以证明,如果不正确,请举出反例.
【答案】(1)见解析;(2)命题①正确,证明见解析;命题②不正确,反例见解析
【详解】(1)∵false是false边上的中线,
∴false,同理false,
∵false,∴false,
∵false,false,
∴false,
∴false,
∵false,false,
∴false;
(2)命题①正确,已知如图1、图2,
在false和false中,false,false,false是false边false上的中线,false是false边false上的中线,且false.
求证:false.
证明:延长false到false,使false,连接false,延长false到false,使false,连接false.
∵false是false边false上的中线,
∴BD=DC,
∵false
∴false(SAS),
∴false,false,
同理:false,false,
∵false,false.
∵false,false,false,
∴false,false,
∴false,
∴false,false,
∴false,
∴false,即false,
∵false,false,
∴false;
命题②不正确,如图3、图4,
在false和false中,false,false,false边上的高线为false,false边上的高线为false,false,false与false不全等.
7.如图,直线false分别与false轴,false轴交于点false,false,过点false的直线false交false轴于点.false为false的中点,false为射线false上一动点,连结false,false,过false作false于点false.
(1)直接写出点false,false的坐标:false(______,______),false(______,______);
(2)当false为false中点时,求false的长;
(3)当false是以false为腰的等腰三角形时,求点false坐标;
(4)当点false在线段false(不与false,重合)上运动时,作false关于false的对称点false,若false落在false轴上,则false的长为_______.
【答案】(1)-2,0;2,0;(2)false;(3)当false或false时,false是以false为腰的等腰三角形;(4)false.
【解】令y=0,得x=-2,
∴false,
令x=0,得y=4,∴B(0,4)
把B(0,4)代入false,求得b=4,
∴直线BC的解析式为false
令y=0,得x=4,∴false
∵false为false的中点
∴false
故答案为:-2,0;2,0;
(2)由(1)得B(0,4),false
当false为false的中点时,则false,
∵false为false的中点,
∴false轴,
false,false,
∴false
∵false,
∴false
(3)∵点false是射线false上一动点,设false,当false是以false为腰的等腰三角形时,
①若false,false,解得:false,false(舍去),此时false;
②若false,false,解得:false,此时false.
综上,当false或false时,false是以false为腰的等腰三角形.
(4)∵false关于false的对称点false,若false落在false轴上
∴点false为A点,
∴AD=PD=4,
设false,作PF⊥AC于F点,
∴DF=2-x,PF=-x+4,
在Rt△PFD中,DF2+PF2=DP2
即(2-x)2+(-x+4)2=42
解得x=3-false(3+false舍去)
∴P(3-false,false+1),
∴false=false=false
故答案为:false.
同课章节目录
