20.4一次函数的应用-沪教版(上海)八年级数学第二学期同步练习(Word版 含答案)
文档属性
| 名称 | 20.4一次函数的应用-沪教版(上海)八年级数学第二学期同步练习(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 274.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-12 00:00:00 | ||
图片预览



文档简介
20.4一次函数的应用
一、单选题
1.用长为50的栏杆围成一个长为x宽为y的长方形,则y与x的函数关系为(
)
A.y=25-x
B.y=25+x
C.y=50-x
D.y=50+x
2.某水电站蓄水池有2个进水口,1个出水口,每个进水口进水量与时间x的关系为,出水口出水量与时间x的关系为,已知某天0点到6点,进行机组试运行,试机时至少打开1个水口,且水池的蓄水量V与时间的关系.如图所示:给出以下判断:①0到3点只进水不出水;②3点到4点,不进水只出水;③4点到6点不进水也不出水.则上述判断中一定正确的是(
)
A.①
B.②
C.②③
D.①③
3.甲、乙两人从公司去健身房,甲先步行前往,几分钟后乙乘出租车追赶,出租车的速度是甲步行速度的5倍,乙追上甲后,立刻带上甲一同前往,结果甲比预计早到4分钟,他们距公司的路程y(米)与时间x(分)间的函数关系如图所示,则下列结论中正确的个数为( )
①甲步行的速度为100米/分;②乙比甲晚出发7分钟;③公司距离健身房1500米;④乙追上甲时距健身房500米.
A.1个
B.2个
C.3个
D.4个
4.甲、乙两辆汽车分别从、两地同时出发,沿同一条公路相向而行,乙车出发后休息,与甲车相遇后,继续行驶.设甲、乙两车与地的距离分别为、,甲车行驶的时间为,、与之间的函数图象如图所示,结合图象下列说法不正确的是
A.甲车的速度是
B.乙车休息前的速度为
C.甲走到时用时
D.乙车休息了1小时
5.甲、乙两人在笔直的人行道上同起点、同终点、同方向匀速步行1800米,先到终点的人原地休息.已知甲先出发3分钟,在整个步行过程中,甲、乙两人间的距离(米与甲出发后步行的时间(分之间的关系如图所示,下列结论:①甲步行的速度为60米分;②乙走完全程用了22.5分钟;③乙用9分钟追上甲;④乙到达终点时,甲离终点还有270米.其中正确的结论有
A.1个
B.2个
C.3个
D.4个
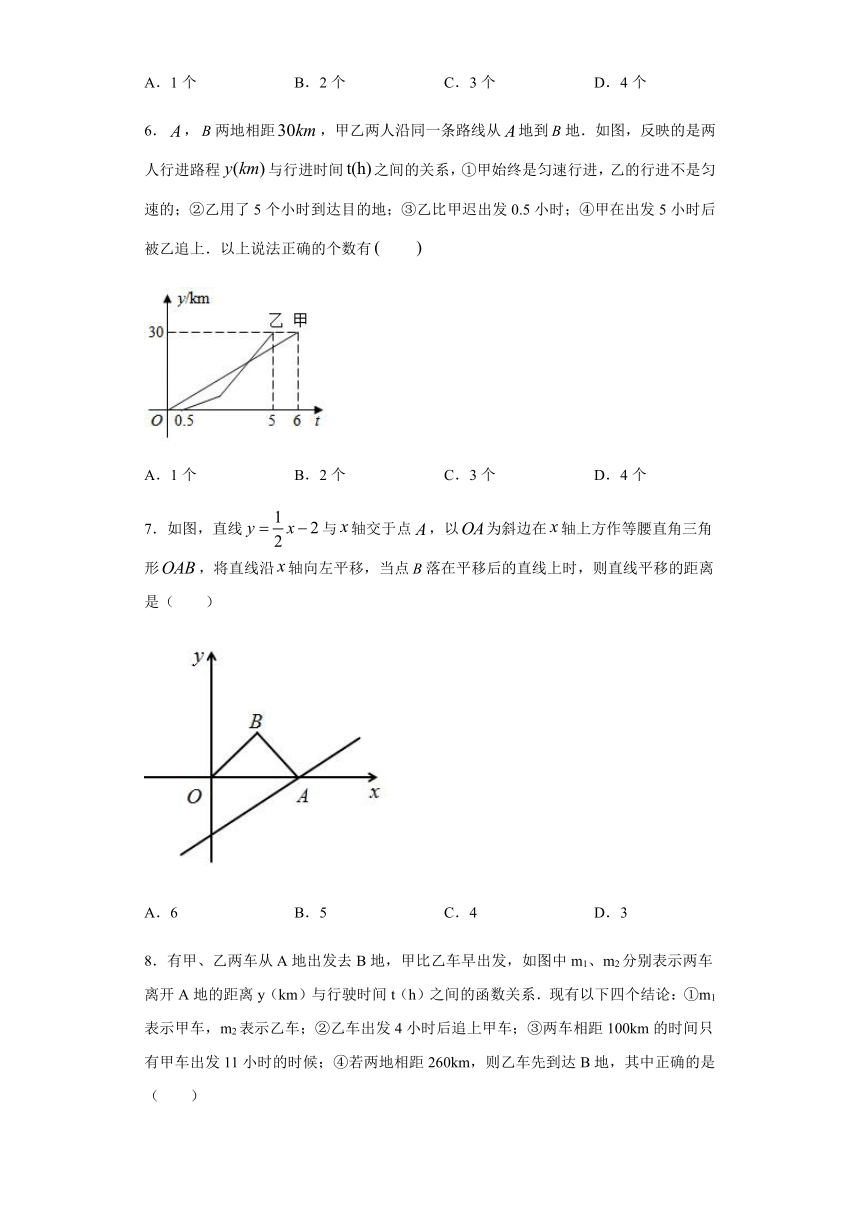
6.,两地相距,甲乙两人沿同一条路线从地到地.如图,反映的是两人行进路程与行进时间之间的关系,①甲始终是匀速行进,乙的行进不是匀速的;②乙用了5个小时到达目的地;③乙比甲迟出发0.5小时;④甲在出发5小时后被乙追上.以上说法正确的个数有
A.1个
B.2个
C.3个
D.4个
7.如图,直线与轴交于点,以为斜边在轴上方作等腰直角三角形,将直线沿轴向左平移,当点落在平移后的直线上时,则直线平移的距离是(
)
A.6
B.5
C.4
D.3
8.有甲、乙两车从A地出发去B地,甲比乙车早出发,如图中m1、m2分别表示两车离开A地的距离y(km)与行驶时间t(h)之间的函数关系.现有以下四个结论:①m1表示甲车,m2表示乙车;②乙车出发4小时后追上甲车;③两车相距100km的时间只有甲车出发11小时的时候;④若两地相距260km,则乙车先到达B地,其中正确的是(
)
A.①②③④
B.②③④
C.①②③
D.①②④
9.如图所示,直线y=x+4与两坐标轴分别交于A、B两点,点C是OB的中点,D、E分别是直线AB、y轴上的动点,则周长的最小值是(
)
A.
B.
C.
D.
10.在运动会径赛中,甲、乙两人同时起跑,刚跑出米甲不慎摔倒,他又迅速地爬起来继续投入比赛.他们所跑的路程与比赛时间的关系如图,有下列说法:
①他们进行的是比赛;
②乙全程的平均速度为
③甲摔倒之前,乙的速度快:
④甲再次投入比赛后的平均速度为;
⑤甲再次投入比赛后在距离终点米时追上了乙
其中正确的个数有(
)
A.1
B.2
C.3
D.4
二、填空题
11.小明同学骑自行车从家里出发依次去甲、乙两个景点游玩,他离家的距离与所用的时间之间的函数图像如图所示:
(1)甲景点与乙景点相距___________千米,乙景点与小明家距离是___________千米;
(2)当时,y与x的函数关系式是___________;
(3)小明在游玩途中,停留所用时间为___________小时,在6小时内共骑行___________千米.
12.高台与张掖两地之间的距离是120千米,若汽车以平均每小时40千米的速度从高台开往张掖,则汽车距张掖的路程y
(千米)与行驶的时间x
(小时)之间的函数关系式为__________;
13.小南和小开在一条笔直的道路上练习跑步,小南先从起点出发匀速跑向终点,小南出发一段时间后,小开才从起点出发匀速追赶小南,小开追上小南后立即掉头以原速度的匀速返回起点(掉头时间忽略不计).小南与小开之间的距离(米)与小南跑步的时间(分)之间的函数关系如图所示,则当小开刚回到起点时,小南距离终点还有______米.
14.甲、乙两车同时从A地出发,沿同一条笔直的公路匀速前往相距的B地,半小时后甲发现有东西落在A地,于是立即以原速返回A地取物品,取到物品后立即以原来速度的1.2倍继续前往B地(所有掉头时间和领取物品的时间忽略不计),甲、乙两车之间的距离与甲车驶的时间之间的部分函数关系如图所示,当甲车到达B地时,乙车离B地的距离是___________.
15.小华的家和妈妈经营的商店位于一条笔直的公路上,某天早上,小华从家里出发,匀速步行去妈妈的商店帮忙,同时妈妈骑三轮车从商店出发,沿同一条路匀速回家装载货物,然后按原路原速返回商店,小华到达商店比妈妈返回商店早5分钟,在此过程中,设妈妈从商店出发开始所用时间为t(分钟),图中表示两人之间的距离s(米)与时间t(分钟)的函数关系的图象,妈妈装载货物花了__________________分钟.
三、解答题
16.如图1,在A,B两地之间有汽车站C,客车由A地驶往C站,货车由B地驶往A地,两车同时出发,匀速行驶.客车离C站的距离y1(km)、货车离C站的距离y2(km)与行驶时间x(h)之间的关系如图2所示.
(1)A,B两地相距______千米,货车的速度是______千米/时;
(2)出发3小时后,求货车离C站的距离y2(km)与行驶时间x(h)之间的关系式;
(3)两车出发后几小时相遇?
17.某通讯公司推出①②两种收费方式供用户选择,其中一种有月租费,另一种没有月租费,且两种收费方式的通话时间(分钟)与收费(元)的关系如图所示:
(1)分别求出①②两种方案的收费(元)与通话时间(分钟)之间的函数关系式.
(2)当值为多少时两种方案收费相等.
(3)当值为多少时,第②种方案比第一种方案每个月多元?
18.为深入推进“健康沈阳”建设,倡导全民参与健身,我市举行“健康沈阳,重阳登高”活动,广大市民踊跃参加.甲乙两人同时登山,2分钟后乙开始提速,且提速后乙登高速度是甲登山速度的3倍,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山的速度是每分钟
米,乙在A地提速时距地面的高度b为
米,乙在距地而高度为300米时对应的时间t是
分钟;
(2)请分别求出线段AB、CD所对应的函数关系式(需写出自变量的取值范围);
(3)登山
分时,甲、乙两人距地面的高度差为70米?
参考答案
1.A
2.A
3.C
4.D
5.D
6.B
7.A
8.D
9.D
10.C
11.(1)6,12;(2)y=6x;(3)3,24
12.y=120-40x(0≤x≤3)
13.280
14.
15.5
16.(1)600;40;(2);(3)两车出发后5小时相遇.
17.(1)①y1=0.1x+30;②y2=0.2x;(2)当通话时间300分钟时,两种方案收费相等.(3)当值为600时,第②种方案比第①种方案每个月多.
18.(1)10,30,11;(2)线段AB对应的函数解析式为y=30x﹣30(2≤x≤11);线段CD所对应的函数关系式是y=10x+100(0≤x≤20);(3)3、10或13
一、单选题
1.用长为50的栏杆围成一个长为x宽为y的长方形,则y与x的函数关系为(
)
A.y=25-x
B.y=25+x
C.y=50-x
D.y=50+x
2.某水电站蓄水池有2个进水口,1个出水口,每个进水口进水量与时间x的关系为,出水口出水量与时间x的关系为,已知某天0点到6点,进行机组试运行,试机时至少打开1个水口,且水池的蓄水量V与时间的关系.如图所示:给出以下判断:①0到3点只进水不出水;②3点到4点,不进水只出水;③4点到6点不进水也不出水.则上述判断中一定正确的是(
)
A.①
B.②
C.②③
D.①③
3.甲、乙两人从公司去健身房,甲先步行前往,几分钟后乙乘出租车追赶,出租车的速度是甲步行速度的5倍,乙追上甲后,立刻带上甲一同前往,结果甲比预计早到4分钟,他们距公司的路程y(米)与时间x(分)间的函数关系如图所示,则下列结论中正确的个数为( )
①甲步行的速度为100米/分;②乙比甲晚出发7分钟;③公司距离健身房1500米;④乙追上甲时距健身房500米.
A.1个
B.2个
C.3个
D.4个
4.甲、乙两辆汽车分别从、两地同时出发,沿同一条公路相向而行,乙车出发后休息,与甲车相遇后,继续行驶.设甲、乙两车与地的距离分别为、,甲车行驶的时间为,、与之间的函数图象如图所示,结合图象下列说法不正确的是
A.甲车的速度是
B.乙车休息前的速度为
C.甲走到时用时
D.乙车休息了1小时
5.甲、乙两人在笔直的人行道上同起点、同终点、同方向匀速步行1800米,先到终点的人原地休息.已知甲先出发3分钟,在整个步行过程中,甲、乙两人间的距离(米与甲出发后步行的时间(分之间的关系如图所示,下列结论:①甲步行的速度为60米分;②乙走完全程用了22.5分钟;③乙用9分钟追上甲;④乙到达终点时,甲离终点还有270米.其中正确的结论有
A.1个
B.2个
C.3个
D.4个
6.,两地相距,甲乙两人沿同一条路线从地到地.如图,反映的是两人行进路程与行进时间之间的关系,①甲始终是匀速行进,乙的行进不是匀速的;②乙用了5个小时到达目的地;③乙比甲迟出发0.5小时;④甲在出发5小时后被乙追上.以上说法正确的个数有
A.1个
B.2个
C.3个
D.4个
7.如图,直线与轴交于点,以为斜边在轴上方作等腰直角三角形,将直线沿轴向左平移,当点落在平移后的直线上时,则直线平移的距离是(
)
A.6
B.5
C.4
D.3
8.有甲、乙两车从A地出发去B地,甲比乙车早出发,如图中m1、m2分别表示两车离开A地的距离y(km)与行驶时间t(h)之间的函数关系.现有以下四个结论:①m1表示甲车,m2表示乙车;②乙车出发4小时后追上甲车;③两车相距100km的时间只有甲车出发11小时的时候;④若两地相距260km,则乙车先到达B地,其中正确的是(
)
A.①②③④
B.②③④
C.①②③
D.①②④
9.如图所示,直线y=x+4与两坐标轴分别交于A、B两点,点C是OB的中点,D、E分别是直线AB、y轴上的动点,则周长的最小值是(
)
A.
B.
C.
D.
10.在运动会径赛中,甲、乙两人同时起跑,刚跑出米甲不慎摔倒,他又迅速地爬起来继续投入比赛.他们所跑的路程与比赛时间的关系如图,有下列说法:
①他们进行的是比赛;
②乙全程的平均速度为
③甲摔倒之前,乙的速度快:
④甲再次投入比赛后的平均速度为;
⑤甲再次投入比赛后在距离终点米时追上了乙
其中正确的个数有(
)
A.1
B.2
C.3
D.4
二、填空题
11.小明同学骑自行车从家里出发依次去甲、乙两个景点游玩,他离家的距离与所用的时间之间的函数图像如图所示:
(1)甲景点与乙景点相距___________千米,乙景点与小明家距离是___________千米;
(2)当时,y与x的函数关系式是___________;
(3)小明在游玩途中,停留所用时间为___________小时,在6小时内共骑行___________千米.
12.高台与张掖两地之间的距离是120千米,若汽车以平均每小时40千米的速度从高台开往张掖,则汽车距张掖的路程y
(千米)与行驶的时间x
(小时)之间的函数关系式为__________;
13.小南和小开在一条笔直的道路上练习跑步,小南先从起点出发匀速跑向终点,小南出发一段时间后,小开才从起点出发匀速追赶小南,小开追上小南后立即掉头以原速度的匀速返回起点(掉头时间忽略不计).小南与小开之间的距离(米)与小南跑步的时间(分)之间的函数关系如图所示,则当小开刚回到起点时,小南距离终点还有______米.
14.甲、乙两车同时从A地出发,沿同一条笔直的公路匀速前往相距的B地,半小时后甲发现有东西落在A地,于是立即以原速返回A地取物品,取到物品后立即以原来速度的1.2倍继续前往B地(所有掉头时间和领取物品的时间忽略不计),甲、乙两车之间的距离与甲车驶的时间之间的部分函数关系如图所示,当甲车到达B地时,乙车离B地的距离是___________.
15.小华的家和妈妈经营的商店位于一条笔直的公路上,某天早上,小华从家里出发,匀速步行去妈妈的商店帮忙,同时妈妈骑三轮车从商店出发,沿同一条路匀速回家装载货物,然后按原路原速返回商店,小华到达商店比妈妈返回商店早5分钟,在此过程中,设妈妈从商店出发开始所用时间为t(分钟),图中表示两人之间的距离s(米)与时间t(分钟)的函数关系的图象,妈妈装载货物花了__________________分钟.
三、解答题
16.如图1,在A,B两地之间有汽车站C,客车由A地驶往C站,货车由B地驶往A地,两车同时出发,匀速行驶.客车离C站的距离y1(km)、货车离C站的距离y2(km)与行驶时间x(h)之间的关系如图2所示.
(1)A,B两地相距______千米,货车的速度是______千米/时;
(2)出发3小时后,求货车离C站的距离y2(km)与行驶时间x(h)之间的关系式;
(3)两车出发后几小时相遇?
17.某通讯公司推出①②两种收费方式供用户选择,其中一种有月租费,另一种没有月租费,且两种收费方式的通话时间(分钟)与收费(元)的关系如图所示:
(1)分别求出①②两种方案的收费(元)与通话时间(分钟)之间的函数关系式.
(2)当值为多少时两种方案收费相等.
(3)当值为多少时,第②种方案比第一种方案每个月多元?
18.为深入推进“健康沈阳”建设,倡导全民参与健身,我市举行“健康沈阳,重阳登高”活动,广大市民踊跃参加.甲乙两人同时登山,2分钟后乙开始提速,且提速后乙登高速度是甲登山速度的3倍,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山的速度是每分钟
米,乙在A地提速时距地面的高度b为
米,乙在距地而高度为300米时对应的时间t是
分钟;
(2)请分别求出线段AB、CD所对应的函数关系式(需写出自变量的取值范围);
(3)登山
分时,甲、乙两人距地面的高度差为70米?
参考答案
1.A
2.A
3.C
4.D
5.D
6.B
7.A
8.D
9.D
10.C
11.(1)6,12;(2)y=6x;(3)3,24
12.y=120-40x(0≤x≤3)
13.280
14.
15.5
16.(1)600;40;(2);(3)两车出发后5小时相遇.
17.(1)①y1=0.1x+30;②y2=0.2x;(2)当通话时间300分钟时,两种方案收费相等.(3)当值为600时,第②种方案比第①种方案每个月多.
18.(1)10,30,11;(2)线段AB对应的函数解析式为y=30x﹣30(2≤x≤11);线段CD所对应的函数关系式是y=10x+100(0≤x≤20);(3)3、10或13
