山东省临沂市2020-2021学年高三上学期期末检测数学试题(word解析版)
文档属性
| 名称 | 山东省临沂市2020-2021学年高三上学期期末检测数学试题(word解析版) |  | |
| 格式 | docx | ||
| 文件大小 | 989.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-13 21:20:03 | ||
图片预览




文档简介
山东省临沂市2021届高三第一学期期末检测
数学试卷
一、单项选择题(本大题共8小题,每小题5分,共计40分.在每小题给出的四个选项中,只有一个是符合题目要求的,请把答案添涂在答题卡相应位置上)
1.已知集合A={﹣1,2},B=,若AB=A,则所有符合条件的实数m组成的集合是
A.{,0,1}
B.{﹣1,0,2}
C.{﹣1,2}
D.{﹣1,0,}
2.复数z满足,则=
A.
B.
C.
D.
3.若向量=(x,2),=(2,3),=(2,﹣4),且∥,则=
A.3
B.
C.
D.
4.在数列中,,,若为等差数列,则=
A.
B.
C.
D.
5.“”是“”的
A.充要条件
B.充分不必要条件
C.必要不充分条件
D.既不充分也不必要条件
6.函数的部分图象大致为
7.抛物线有如下光学性质:过焦点的光线经抛物线反射之后得到的光线平行于抛物线的对称轴;反之,平行于抛物线对称轴的入射光线经拋物线反射后必过拋物线的焦点.已知抛物线y2=4x的焦点为F,一条平行于x轴的光线从点M(3,1)射出,经过抛物线上的点A反射后,再经抛物线上的另一点B射出,则△ABM的周长为
A.
B.
C.
D.
8.函数的图象关于y轴对称,x(,0]时,,.又,则的解集为
A.(3,)
B.
C.(1,)
D.
二、?多项选择题(本大题共4小题,每小题5分,?共计20分.在每小题给出的四个选项中,至少有两个是符合题目要求的,请把答案添涂在答题卡相应位置上)
9.某研究机构为了实时掌握当地新增高速运行情况,在某服务区从小型汽车中抽取了80名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90],得到如图所示的频率分布直方图.下列结论正确的是
A.这80辆小型车辆车速的众数的估计值为77.5
B.在该服务区任意抽取一辆车,估计车速超过75km/h
的概率为0.65
C.若从样本中车速在[60,70)的车辆中任意抽取2辆,
则至少有一辆车的车速在[65,70)的概率为
D.若从样本中车速在[60,70)的车辆中任意抽取2辆,
第9题
则车速都在[65,70)内的概率为
10.在棱长为1的正方体ABCD—A1B1C1D1中,点M在棱CC1上,则下列结论正确的是
A.直线BM与平面ADD1A1平行
B.平面BMD1截正方体所得的截面为三角形
C.异面直线AD1与A1C1所成的角为
D.的最小值为
11.已知圆C:x2+y2=4,直线l:(3+m)x+4y﹣3+3m=0(mR).则下列四个命题正确的是
A.直线l恒过定点(﹣3,3)
B.当m=0时,圆C上有且仅有三个点到直线l的距离都等于1
C.圆C与曲线:x2+y2﹣6x﹣8y+m=0恰有三条公切线,则m=16
D.当m=13时,直线l上一个动点P向圆C引两条切线PA,PB,其中A,B为切点,则直线AB经过点(,)
12.已知函数,则以下结论正确的是
A.在R上单调递增
B.
C.方程有实数解
D.存在实数k,使得方程有4个实数解
A.0
B.1
C.2
D.3
三、填空题(本大题共4小题,?每小题5分,共计20分.请把答案填写在答题卡相应位置上)
13.已知,若(0,),则=
.
14.的展开式中的系数为
.
15.有六条线段,其长度分别为2,3,4,5,6,7.现任取三条,则这三条线段在可以构成三角形的前提下,能构成锐角三角形的概率是
.
16.正方体ABCD—A1B1C1D1的棱长为2,动点P在对角线BD1上,当PB=时,三棱锥P—ABC的外接球的体积为
.
四、解答题(本大题共6小题,共计70分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)
正项等比数列的前n项和为,,若,,且点(,)在函数的图像上.
(1)求,的通项公式;
(2)记,求的前n项和.
18.(本小题满分12分)
已知△ABC的内角A,B,C的对边分别为a,b,c,若
,且△ABC的外接圆的面积为3,△ABC的面积为,求△ABC的周长.
在①bsin2A﹣asinAcosC=csin2A;②bsin=asinB;③2acosB=2c﹣b这三个条件中任选一个补充在上面问题中,并加以解答.(注:如果选择多个条件分别解答,按第一个解答计分.)
19.(本小题满分12分)
如图,四边形ABCD为直角梯形,AB∥CD,AB⊥BC,AB=2BC=2,CD=3BC,E为AB的中点,点F在CD上,且EF∥BC,以EF为折痕把四边形EBCF折起,使二面角B—EF—D为直角,点B,C折起后的位置分别记为点G,H.
(1)求证:AD⊥平面AHF;
(2)在线段HD上存在一点P,使平面PAE与平面AEG所成的二面角的余弦值为,延长GH到点M,使HM=GH,判断直线PM是否在平面PAE中,说明理由.
20.(本小题满分12分)
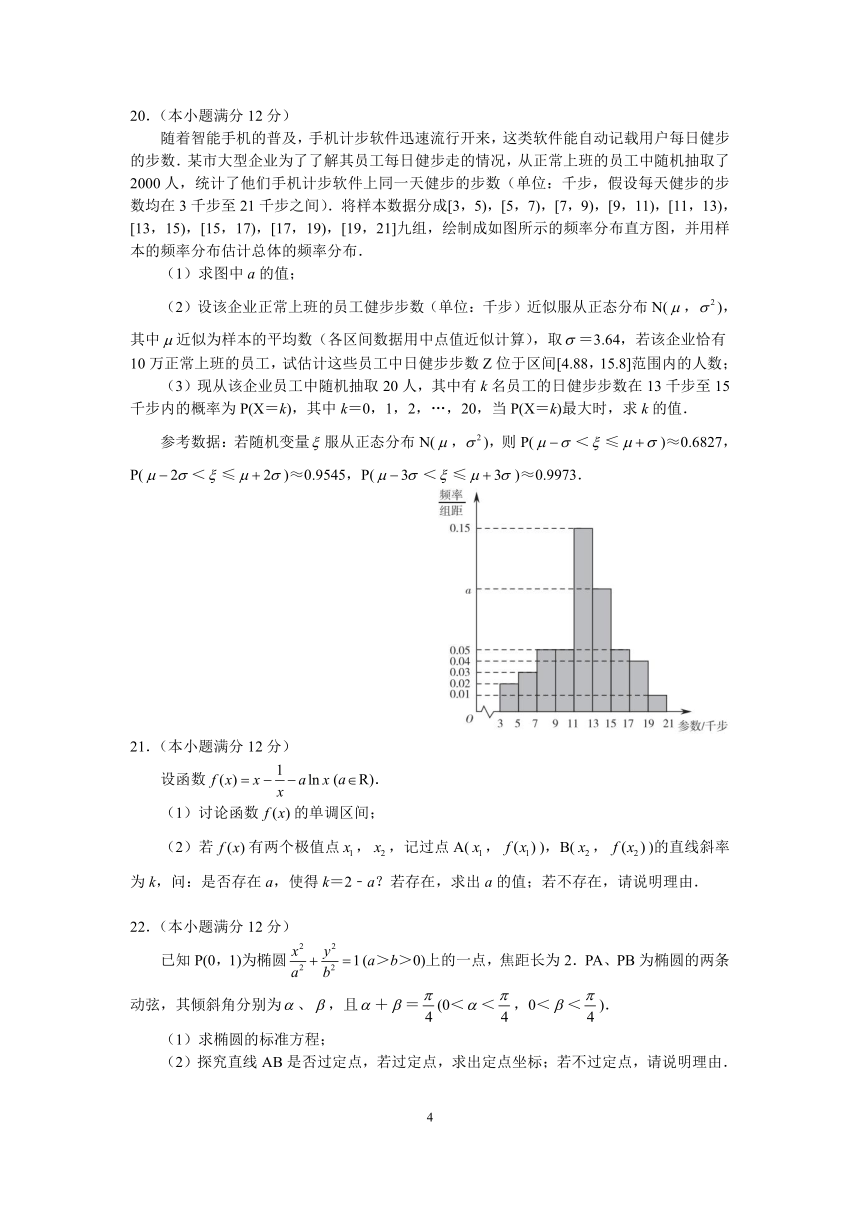
随着智能手机的普及,手机计步软件迅速流行开来,这类软件能自动记载用户每日健步的步数.某市大型企业为了了解其员工每日健步走的情况,从正常上班的员工中随机抽取了2000人,统计了他们手机计步软件上同一天健步的步数(单位:千步,假设每天健步的步数均在3千步至21千步之间).将样本数据分成[3,5),[5,7),[7,9),[9,11),[11,13),[13,15),[15,17),[17,19),[19,21]九组,绘制成如图所示的频率分布直方图,并用样本的频率分布估计总体的频率分布.
(1)求图中a的值;
(2)设该企业正常上班的员工健步步数(单位:千步)近似服从正态分布N(,),其中近似为样本的平均数(各区间数据用中点值近似计算),取=3.64,若该企业恰有10万正常上班的员工,试估计这些员工中日健步步数Z位于区间[4.88,15.8]范围内的人数;
(3)现从该企业员工中随机抽取20人,其中有k名员工的日健步步数在13千步至15千步内的概率为P(X=k),其中k=0,1,2,…,20,当P(X=k)最大时,求k的值.
参考数据:若随机变量服从正态分布N(,),则P(<≤)≈0.6827,P(<≤)≈0.9545,P(<≤)≈0.9973.
21.(本小题满分12分)
设函数(aR).
(1)讨论函数的单调区间;
(2)若有两个极值点,,记过点A(,),B(,)的直线斜率为k,问:是否存在a,使得k=2﹣a?若存在,求出a的值;若不存在,请说明理由.
22.(本小题满分12分)
已知P(0,1)为椭圆(a>b>0)上的一点,焦距长为2.PA、PB为椭圆的两条动弦,其倾斜角分别为、,且+=(0<<,0<<).
(1)求椭圆的标准方程;
(2)探究直线AB是否过定点,若过定点,求出定点坐标;若不过定点,请说明理由.
山东省临沂市2021届高三第一学期期末检测
数学试卷
一、单项选择题(本大题共8小题,每小题5分,共计40分.在每小题给出的四个选项中,只有一个是符合题目要求的,请把答案添涂在答题卡相应位置上)
1.已知集合A={﹣1,2},B=,若AB=A,则所有符合条件的实数m组成的集合是
A.{,0,1}
B.{﹣1,0,2}
C.{﹣1,2}
D.{﹣1,0,}
答案:D
解析:若AB=A,则BA,①当B=,即m=0,符合题意;②当B≠时,即m≠0,此时B={},要使BA,则=﹣1或2,则m=﹣1或.故选D.
2.复数z满足,则=
A.
B.
C.
D.
答案:C
解析:.故选C.
3.若向量=(x,2),=(2,3),=(2,﹣4),且∥,则=
A.3
B.
C.
D.
答案:C
解析:因为向量=(x,2),=(2,﹣4),且∥,
所以,所以=(﹣1,2),故=(﹣3,﹣1),
所以.故选C.
4.在数列中,,,若为等差数列,则=
A.
B.
C.
D.
答案:A
解析:.故选A.
5.“”是“”的
A.充要条件
B.充分不必要条件
C.必要不充分条件
D.既不充分也不必要条件
答案:C
解析:因为,所以,又因为(﹣2,﹣1)(,0),故选C.
6.函数的部分图象大致为
答案:B
解析:首先判断出该函数是奇函数,排除D,其次该函数与x轴的交点坐标为(1,0),(﹣1,0),排除A,又,排除C,故选B.
7.抛物线有如下光学性质:过焦点的光线经抛物线反射之后得到的光线平行于抛物线的对称轴;反之,平行于抛物线对称轴的入射光线经拋物线反射后必过拋物线的焦点.已知抛物线y2=4x的焦点为F,一条平行于x轴的光线从点M(3,1)射出,经过抛物线上的点A反射后,再经抛物线上的另一点B射出,则△ABM的周长为
A.
B.
C.
D.
答案:B
解析:根据题意可求得A(,1),B(4,﹣4),从而AM=,AB=,MB=,故△ABM的周长为.故选B.
8.函数的图象关于y轴对称,x(,0]时,,.又,则的解集为
A.(3,)
B.
C.(1,)
D.
答案:A
解析:根据函数的图象关于y轴对称,x(,0]时,,,可得当>0,有x<﹣2或x>2,当<0,有﹣2<x<2,
可转化为或,解得x>3,选A.
二、?多项选择题(本大题共4小题,每小题5分,?共计20分.在每小题给出的四个选项中,至少有两个是符合题目要求的,请把答案添涂在答题卡相应位置上)
9.某研究机构为了实时掌握当地新增高速运行情况,在某服务区从小型汽车中抽取了80名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90],得到如图所示的频率分布直方图.下列结论正确的是
A.这80辆小型车辆车速的众数的估计值为77.5
B.在该服务区任意抽取一辆车,估计车速超过75km/h
的概率为0.65
C.若从样本中车速在[60,70)的车辆中任意抽取2辆,
则至少有一辆车的车速在[65,70)的概率为
D.若从样本中车速在[60,70)的车辆中任意抽取2辆,
第9题
则车速都在[65,70)内的概率为
答案:ABC
解析:众数=,故A正确;车速超过75km/h的概率=(0.06+0.05+0.02)×5=0.65,故B正确;求得车速在[60,65)的车有4辆,车速在[65,70)的车有8辆,从[60,70)的车辆中任意抽取2辆,至少有一辆车车速在[65,70)的概率=,故C正确;从样本中车速在[60,70)的车辆中任意抽取2辆,则车速都在[65,70)内的概率为,故D错误.综上选ABC.
10.在棱长为1的正方体ABCD—A1B1C1D1中,点M在棱CC1上,则下列结论正确的是
A.直线BM与平面ADD1A1平行
B.平面BMD1截正方体所得的截面为三角形
C.异面直线AD1与A1C1所成的角为
D.的最小值为
答案:AC
解析:若N为AA1上一点,使A1N=CM,则四边形BMD1N就是平面BMD1截正方体所得的截面,故B错误;的最小值为,故D错误.综上选AC.
11.已知圆C:x2+y2=4,直线l:(3+m)x+4y﹣3+3m=0(mR).则下列四个命题正确的是
A.直线l恒过定点(﹣3,3)
B.当m=0时,圆C上有且仅有三个点到直线l的距离都等于1
C.圆C与曲线:x2+y2﹣6x﹣8y+m=0恰有三条公切线,则m=16
D.当m=13时,直线l上一个动点P向圆C引两条切线PA,PB,其中A,B为切点,则直线AB经过点(,)
答案:ACD
解析:因为直线l:(3+m)x+4y﹣3+3m=0(mR),整理得:,故直线l恒过定点(﹣3,3),A正确;当m=0时,直线l:3x+4y﹣3=0,求得圆心C到直线的距离为,,故圆C上有四个点到直线l的距离都等于1,B错误;曲线:x2+y2﹣6x﹣8y+m=0是以(3,4)为圆心,为半径的圆,若圆C与曲线:x2+y2﹣6x﹣8y+m=0恰有三条公切线,则,则m=16,故C正确;当m=13时,直线l为,设动点P为(p,﹣4p﹣9),过P向圆C引两条切线PA,PB,则直线AB方程为:,整理得
,故直线AB过定点(,),故D正确.综上选ACD.
12.已知函数,则以下结论正确的是
A.在R上单调递增
B.
C.方程有实数解
D.存在实数k,使得方程有4个实数解
答案:BCD
解析:,故A错误;当x>﹣3时,,所以在(﹣3,)单调递增,因为,所以,故B正确;在(﹣3,)单调递增,在(,﹣3)单调递减,,,故在(﹣3,0)上,方程有实数解,C正确;,显然x=0是原方程的根,当x≠0时,,令,,列表如下:
x
(,﹣2)
﹣2
(﹣2,0)
(0,)
﹢
0
﹣
﹢
单调递增
单调递减
单调递增
故当0<k<,直线y=k与函数(x≠0)有三个交点,又x=0是原方程的根,故存在实数k,使得方程有4个实数解,D正确.综上选BCD.
三、填空题(本大题共4小题,?每小题5分,共计20分.请把答案填写在答题卡相应位置上)
13.已知,若(0,),则=
.
答案:或
解析:,
(,),或,故=或.
14.的展开式中的系数为
.
答案:25
解析:的第r+1项为,故原式展开式中的系数=.
15.有六条线段,其长度分别为2,3,4,5,6,7.现任取三条,则这三条线段在可以构成三角形的前提下,能构成锐角三角形的概率是
.
答案:
解析:从长度为2,3,4,5,6,7的六条线段中任取三条,构成三角形的可能性有13种,其中能构成锐角三角形的有3种,故概率为.
16.正方体ABCD—A1B1C1D1的棱长为2,动点P在对角线BD1上,当PB=时,三棱锥P—ABC的外接球的体积为
.
答案:
解析:由题意可知,P是正方体对角线BD1的中点,取AC中点Q,则三棱锥P—ABC的外接球的球心在直线PQ上,设球的半径为R,则,解得R=,故V=.
四、解答题(本大题共6小题,共计70分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)
正项等比数列的前n项和为,,若,,且点(,)在函数的图像上.
(1)求,的通项公式;
(2)记,求的前n项和.
解:(1)设数列的公比为q,由题意可得,
解得:或(舍),,
故的通项公式为,
因为点(,)在函数的图像上,所以,
所以.
(2)由题意知,
.
18.(本小题满分12分)
已知△ABC的内角A,B,C的对边分别为a,b,c,若
,且△ABC的外接圆的面积为3,△ABC的面积为,求△ABC的周长.
在①bsin2A﹣asinAcosC=csin2A;②bsin=asinB;③2acosB=2c﹣b这三个条件中任选一个补充在上面问题中,并加以解答.(注:如果选择多个条件分别解答,按第一个解答计分.)
解:若选①由bsin2A﹣asinAcosC=csin2A及正弦定理可得:
,
A(0,π),,,
所以,
所以,,
因为△ABC的外接圆的面积为3π,由正弦定理可得,,
又△ABC的面积为,所以,即,所以.
由余弦定理得,则,
所以,即,
所以△ABC的周长;
若选②,由正弦定理得,
因为,所以,
由,可得,故,
因为,故,
因此.
其余步骤同①
若选③,由正弦定理可得,,
将,
代入上式可得,,
所以,
因为,所以,即,由于,所以,
其余步骤同①.
19.(本小题满分12分)
如图,四边形ABCD为直角梯形,AB∥CD,AB⊥BC,AB=2BC=2,CD=3BC,E为AB的中点,点F在CD上,且EF∥BC,以EF为折痕把四边形EBCF折起,使二面角B—EF—D为直角,点B,C折起后的位置分别记为点G,H.
(1)求证:AD⊥平面AHF;
(2)在线段HD上存在一点P,使平面PAE与平面AEG所成的二面角的余弦值为,延长GH到点M,使HM=GH,判断直线PM是否在平面PAE中,说明理由.
解:(1)证明:
∴EF⊥CF,即EF⊥HF,
又∵平面EGHF⊥平面AEFD,平面EGHF平面AEFD=EF,
∴HF⊥平面AEFD,∴HF⊥AD,
∵点E为AB的中点,AB=2BC=2,CD=3BC,AB∥CD,EF∥BC,
∴AE=EF=1,DF=2,
∴AF=,AD=,
又HFAF=F,∴AD⊥平面AHF;
(2)由(1)知HF⊥平面AEFD,EF⊥FD,∴HF⊥FD,HF⊥EF,
如图,以F为原点,FE,FD,FH所在直线分别为x轴,y轴,z轴,
建立空间直角坐标系F—xyz,
则E(1,0,0),D(0,2,0),H(0,0,1),A(1,1,0),G(1,0,1)
,
∴
设平面PAE的法向量为,
则,
令,得,
易知平面AEG的一个法向量为
由,解得
∴P为HD中点,
由,得,又,∴,
又平面PAE的一个法向量
,因为点P在平面PAE内,
∴直线PM在平面PAE内.
20.(本小题满分12分)
随着智能手机的普及,手机计步软件迅速流行开来,这类软件能自动记载用户每日健步的步数.某市大型企业为了了解其员工每日健步走的情况,从正常上班的员工中随机抽取了2000人,统计了他们手机计步软件上同一天健步的步数(单位:千步,假设每天健步的步数均在3千步至21千步之间).将样本数据分成[3,5),[5,7),[7,9),[9,11),[11,13),[13,15),[15,17),[17,19),[19,21]九组,绘制成如图所示的频率分布直方图,并用样本的频率分布估计总体的频率分布.
(1)求图中a的值;
(2)设该企业正常上班的员工健步步数(单位:千步)近似服从正态分布N(,),其中近似为样本的平均数(各区间数据用中点值近似计算),取=3.64,若该企业恰有10万正常上班的员工,试估计这些员工中日健步步数Z位于区间[4.88,15.8]范围内的人数;
(3)现从该企业员工中随机抽取20人,其中有k名员工的日健步步数在13千步至15千步内的概率为P(X=k),其中k=0,1,2,…,20,当P(X=k)最大时,求k的值.
参考数据:若随机变量服从正态分布N(,),则P(<≤)≈0.6827,P(<≤)≈0.9545,P(<≤)≈0.9973.
解:(1)由,
解得.
(2)
则(人),所以日健步步数Z位于区间[4.88,15.8]范围内的人数约为8186人;
(3)设从该企业员工中随机抽取20人日健步步数在13千步至15千步的员工有X人,则X~B(20,0.2),
其中有k名员工的概率为
,其中k=0,1,2,…,20,
记,
当时,,则;
当时,,则,
所以当k=4时,最大.
21.(本小题满分12分)
设函数(aR).
(1)讨论函数的单调区间;
(2)若有两个极值点,,记过点A(,),B(,)的直线斜率为k,问:是否存在a,使得k=2﹣a?若存在,求出a的值;若不存在,请说明理由.
解:(1)的定义域为
令,其判别式
上单调递增,
的两根都小于0,在上故在上单调递增,
③当a>2时,,的两根为
上单调递增,上单调递减;
(2)由(1)知,若有两个极值点,,则只能是情况③,故a>2,
因为
所以
又由(1)知,,于是
若存在,使得,则,即
即
再由(1)知,函数在上单调递增,而,
所以
22.(本小题满分12分)
已知P(0,1)为椭圆(a>b>0)上的一点,焦距长为2.PA、PB为椭圆的两条动弦,其倾斜角分别为、,且+=(0<<,0<<).
(1)求椭圆的标准方程;
(2)探究直线AB是否过定点,若过定点,求出定点坐标;若不过定点,请说明理由.
解:(1)由题意知,所以
所以椭圆的标准方程为;
(2)①当直线AB斜率不存在时,设为,设点A坐标为,点B坐标为,
由于
所以
∴,
所以直线AB斜率不存在时,不符合题意;
②当直线AB斜率存在时,设方程为,点A坐标为,点B坐标为
联立,得,
显然,直线,不经过点(0,1),即,
故有,,
化简得,
所以直线AB为
显然当时,上式成立,直线AB过定点(﹣4,﹣3),
综上,直线AB过定点(﹣4,﹣3).
2
数学试卷
一、单项选择题(本大题共8小题,每小题5分,共计40分.在每小题给出的四个选项中,只有一个是符合题目要求的,请把答案添涂在答题卡相应位置上)
1.已知集合A={﹣1,2},B=,若AB=A,则所有符合条件的实数m组成的集合是
A.{,0,1}
B.{﹣1,0,2}
C.{﹣1,2}
D.{﹣1,0,}
2.复数z满足,则=
A.
B.
C.
D.
3.若向量=(x,2),=(2,3),=(2,﹣4),且∥,则=
A.3
B.
C.
D.
4.在数列中,,,若为等差数列,则=
A.
B.
C.
D.
5.“”是“”的
A.充要条件
B.充分不必要条件
C.必要不充分条件
D.既不充分也不必要条件
6.函数的部分图象大致为
7.抛物线有如下光学性质:过焦点的光线经抛物线反射之后得到的光线平行于抛物线的对称轴;反之,平行于抛物线对称轴的入射光线经拋物线反射后必过拋物线的焦点.已知抛物线y2=4x的焦点为F,一条平行于x轴的光线从点M(3,1)射出,经过抛物线上的点A反射后,再经抛物线上的另一点B射出,则△ABM的周长为
A.
B.
C.
D.
8.函数的图象关于y轴对称,x(,0]时,,.又,则的解集为
A.(3,)
B.
C.(1,)
D.
二、?多项选择题(本大题共4小题,每小题5分,?共计20分.在每小题给出的四个选项中,至少有两个是符合题目要求的,请把答案添涂在答题卡相应位置上)
9.某研究机构为了实时掌握当地新增高速运行情况,在某服务区从小型汽车中抽取了80名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90],得到如图所示的频率分布直方图.下列结论正确的是
A.这80辆小型车辆车速的众数的估计值为77.5
B.在该服务区任意抽取一辆车,估计车速超过75km/h
的概率为0.65
C.若从样本中车速在[60,70)的车辆中任意抽取2辆,
则至少有一辆车的车速在[65,70)的概率为
D.若从样本中车速在[60,70)的车辆中任意抽取2辆,
第9题
则车速都在[65,70)内的概率为
10.在棱长为1的正方体ABCD—A1B1C1D1中,点M在棱CC1上,则下列结论正确的是
A.直线BM与平面ADD1A1平行
B.平面BMD1截正方体所得的截面为三角形
C.异面直线AD1与A1C1所成的角为
D.的最小值为
11.已知圆C:x2+y2=4,直线l:(3+m)x+4y﹣3+3m=0(mR).则下列四个命题正确的是
A.直线l恒过定点(﹣3,3)
B.当m=0时,圆C上有且仅有三个点到直线l的距离都等于1
C.圆C与曲线:x2+y2﹣6x﹣8y+m=0恰有三条公切线,则m=16
D.当m=13时,直线l上一个动点P向圆C引两条切线PA,PB,其中A,B为切点,则直线AB经过点(,)
12.已知函数,则以下结论正确的是
A.在R上单调递增
B.
C.方程有实数解
D.存在实数k,使得方程有4个实数解
A.0
B.1
C.2
D.3
三、填空题(本大题共4小题,?每小题5分,共计20分.请把答案填写在答题卡相应位置上)
13.已知,若(0,),则=
.
14.的展开式中的系数为
.
15.有六条线段,其长度分别为2,3,4,5,6,7.现任取三条,则这三条线段在可以构成三角形的前提下,能构成锐角三角形的概率是
.
16.正方体ABCD—A1B1C1D1的棱长为2,动点P在对角线BD1上,当PB=时,三棱锥P—ABC的外接球的体积为
.
四、解答题(本大题共6小题,共计70分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)
正项等比数列的前n项和为,,若,,且点(,)在函数的图像上.
(1)求,的通项公式;
(2)记,求的前n项和.
18.(本小题满分12分)
已知△ABC的内角A,B,C的对边分别为a,b,c,若
,且△ABC的外接圆的面积为3,△ABC的面积为,求△ABC的周长.
在①bsin2A﹣asinAcosC=csin2A;②bsin=asinB;③2acosB=2c﹣b这三个条件中任选一个补充在上面问题中,并加以解答.(注:如果选择多个条件分别解答,按第一个解答计分.)
19.(本小题满分12分)
如图,四边形ABCD为直角梯形,AB∥CD,AB⊥BC,AB=2BC=2,CD=3BC,E为AB的中点,点F在CD上,且EF∥BC,以EF为折痕把四边形EBCF折起,使二面角B—EF—D为直角,点B,C折起后的位置分别记为点G,H.
(1)求证:AD⊥平面AHF;
(2)在线段HD上存在一点P,使平面PAE与平面AEG所成的二面角的余弦值为,延长GH到点M,使HM=GH,判断直线PM是否在平面PAE中,说明理由.
20.(本小题满分12分)
随着智能手机的普及,手机计步软件迅速流行开来,这类软件能自动记载用户每日健步的步数.某市大型企业为了了解其员工每日健步走的情况,从正常上班的员工中随机抽取了2000人,统计了他们手机计步软件上同一天健步的步数(单位:千步,假设每天健步的步数均在3千步至21千步之间).将样本数据分成[3,5),[5,7),[7,9),[9,11),[11,13),[13,15),[15,17),[17,19),[19,21]九组,绘制成如图所示的频率分布直方图,并用样本的频率分布估计总体的频率分布.
(1)求图中a的值;
(2)设该企业正常上班的员工健步步数(单位:千步)近似服从正态分布N(,),其中近似为样本的平均数(各区间数据用中点值近似计算),取=3.64,若该企业恰有10万正常上班的员工,试估计这些员工中日健步步数Z位于区间[4.88,15.8]范围内的人数;
(3)现从该企业员工中随机抽取20人,其中有k名员工的日健步步数在13千步至15千步内的概率为P(X=k),其中k=0,1,2,…,20,当P(X=k)最大时,求k的值.
参考数据:若随机变量服从正态分布N(,),则P(<≤)≈0.6827,P(<≤)≈0.9545,P(<≤)≈0.9973.
21.(本小题满分12分)
设函数(aR).
(1)讨论函数的单调区间;
(2)若有两个极值点,,记过点A(,),B(,)的直线斜率为k,问:是否存在a,使得k=2﹣a?若存在,求出a的值;若不存在,请说明理由.
22.(本小题满分12分)
已知P(0,1)为椭圆(a>b>0)上的一点,焦距长为2.PA、PB为椭圆的两条动弦,其倾斜角分别为、,且+=(0<<,0<<).
(1)求椭圆的标准方程;
(2)探究直线AB是否过定点,若过定点,求出定点坐标;若不过定点,请说明理由.
山东省临沂市2021届高三第一学期期末检测
数学试卷
一、单项选择题(本大题共8小题,每小题5分,共计40分.在每小题给出的四个选项中,只有一个是符合题目要求的,请把答案添涂在答题卡相应位置上)
1.已知集合A={﹣1,2},B=,若AB=A,则所有符合条件的实数m组成的集合是
A.{,0,1}
B.{﹣1,0,2}
C.{﹣1,2}
D.{﹣1,0,}
答案:D
解析:若AB=A,则BA,①当B=,即m=0,符合题意;②当B≠时,即m≠0,此时B={},要使BA,则=﹣1或2,则m=﹣1或.故选D.
2.复数z满足,则=
A.
B.
C.
D.
答案:C
解析:.故选C.
3.若向量=(x,2),=(2,3),=(2,﹣4),且∥,则=
A.3
B.
C.
D.
答案:C
解析:因为向量=(x,2),=(2,﹣4),且∥,
所以,所以=(﹣1,2),故=(﹣3,﹣1),
所以.故选C.
4.在数列中,,,若为等差数列,则=
A.
B.
C.
D.
答案:A
解析:.故选A.
5.“”是“”的
A.充要条件
B.充分不必要条件
C.必要不充分条件
D.既不充分也不必要条件
答案:C
解析:因为,所以,又因为(﹣2,﹣1)(,0),故选C.
6.函数的部分图象大致为
答案:B
解析:首先判断出该函数是奇函数,排除D,其次该函数与x轴的交点坐标为(1,0),(﹣1,0),排除A,又,排除C,故选B.
7.抛物线有如下光学性质:过焦点的光线经抛物线反射之后得到的光线平行于抛物线的对称轴;反之,平行于抛物线对称轴的入射光线经拋物线反射后必过拋物线的焦点.已知抛物线y2=4x的焦点为F,一条平行于x轴的光线从点M(3,1)射出,经过抛物线上的点A反射后,再经抛物线上的另一点B射出,则△ABM的周长为
A.
B.
C.
D.
答案:B
解析:根据题意可求得A(,1),B(4,﹣4),从而AM=,AB=,MB=,故△ABM的周长为.故选B.
8.函数的图象关于y轴对称,x(,0]时,,.又,则的解集为
A.(3,)
B.
C.(1,)
D.
答案:A
解析:根据函数的图象关于y轴对称,x(,0]时,,,可得当>0,有x<﹣2或x>2,当<0,有﹣2<x<2,
可转化为或,解得x>3,选A.
二、?多项选择题(本大题共4小题,每小题5分,?共计20分.在每小题给出的四个选项中,至少有两个是符合题目要求的,请把答案添涂在答题卡相应位置上)
9.某研究机构为了实时掌握当地新增高速运行情况,在某服务区从小型汽车中抽取了80名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90],得到如图所示的频率分布直方图.下列结论正确的是
A.这80辆小型车辆车速的众数的估计值为77.5
B.在该服务区任意抽取一辆车,估计车速超过75km/h
的概率为0.65
C.若从样本中车速在[60,70)的车辆中任意抽取2辆,
则至少有一辆车的车速在[65,70)的概率为
D.若从样本中车速在[60,70)的车辆中任意抽取2辆,
第9题
则车速都在[65,70)内的概率为
答案:ABC
解析:众数=,故A正确;车速超过75km/h的概率=(0.06+0.05+0.02)×5=0.65,故B正确;求得车速在[60,65)的车有4辆,车速在[65,70)的车有8辆,从[60,70)的车辆中任意抽取2辆,至少有一辆车车速在[65,70)的概率=,故C正确;从样本中车速在[60,70)的车辆中任意抽取2辆,则车速都在[65,70)内的概率为,故D错误.综上选ABC.
10.在棱长为1的正方体ABCD—A1B1C1D1中,点M在棱CC1上,则下列结论正确的是
A.直线BM与平面ADD1A1平行
B.平面BMD1截正方体所得的截面为三角形
C.异面直线AD1与A1C1所成的角为
D.的最小值为
答案:AC
解析:若N为AA1上一点,使A1N=CM,则四边形BMD1N就是平面BMD1截正方体所得的截面,故B错误;的最小值为,故D错误.综上选AC.
11.已知圆C:x2+y2=4,直线l:(3+m)x+4y﹣3+3m=0(mR).则下列四个命题正确的是
A.直线l恒过定点(﹣3,3)
B.当m=0时,圆C上有且仅有三个点到直线l的距离都等于1
C.圆C与曲线:x2+y2﹣6x﹣8y+m=0恰有三条公切线,则m=16
D.当m=13时,直线l上一个动点P向圆C引两条切线PA,PB,其中A,B为切点,则直线AB经过点(,)
答案:ACD
解析:因为直线l:(3+m)x+4y﹣3+3m=0(mR),整理得:,故直线l恒过定点(﹣3,3),A正确;当m=0时,直线l:3x+4y﹣3=0,求得圆心C到直线的距离为,,故圆C上有四个点到直线l的距离都等于1,B错误;曲线:x2+y2﹣6x﹣8y+m=0是以(3,4)为圆心,为半径的圆,若圆C与曲线:x2+y2﹣6x﹣8y+m=0恰有三条公切线,则,则m=16,故C正确;当m=13时,直线l为,设动点P为(p,﹣4p﹣9),过P向圆C引两条切线PA,PB,则直线AB方程为:,整理得
,故直线AB过定点(,),故D正确.综上选ACD.
12.已知函数,则以下结论正确的是
A.在R上单调递增
B.
C.方程有实数解
D.存在实数k,使得方程有4个实数解
答案:BCD
解析:,故A错误;当x>﹣3时,,所以在(﹣3,)单调递增,因为,所以,故B正确;在(﹣3,)单调递增,在(,﹣3)单调递减,,,故在(﹣3,0)上,方程有实数解,C正确;,显然x=0是原方程的根,当x≠0时,,令,,列表如下:
x
(,﹣2)
﹣2
(﹣2,0)
(0,)
﹢
0
﹣
﹢
单调递增
单调递减
单调递增
故当0<k<,直线y=k与函数(x≠0)有三个交点,又x=0是原方程的根,故存在实数k,使得方程有4个实数解,D正确.综上选BCD.
三、填空题(本大题共4小题,?每小题5分,共计20分.请把答案填写在答题卡相应位置上)
13.已知,若(0,),则=
.
答案:或
解析:,
(,),或,故=或.
14.的展开式中的系数为
.
答案:25
解析:的第r+1项为,故原式展开式中的系数=.
15.有六条线段,其长度分别为2,3,4,5,6,7.现任取三条,则这三条线段在可以构成三角形的前提下,能构成锐角三角形的概率是
.
答案:
解析:从长度为2,3,4,5,6,7的六条线段中任取三条,构成三角形的可能性有13种,其中能构成锐角三角形的有3种,故概率为.
16.正方体ABCD—A1B1C1D1的棱长为2,动点P在对角线BD1上,当PB=时,三棱锥P—ABC的外接球的体积为
.
答案:
解析:由题意可知,P是正方体对角线BD1的中点,取AC中点Q,则三棱锥P—ABC的外接球的球心在直线PQ上,设球的半径为R,则,解得R=,故V=.
四、解答题(本大题共6小题,共计70分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)
正项等比数列的前n项和为,,若,,且点(,)在函数的图像上.
(1)求,的通项公式;
(2)记,求的前n项和.
解:(1)设数列的公比为q,由题意可得,
解得:或(舍),,
故的通项公式为,
因为点(,)在函数的图像上,所以,
所以.
(2)由题意知,
.
18.(本小题满分12分)
已知△ABC的内角A,B,C的对边分别为a,b,c,若
,且△ABC的外接圆的面积为3,△ABC的面积为,求△ABC的周长.
在①bsin2A﹣asinAcosC=csin2A;②bsin=asinB;③2acosB=2c﹣b这三个条件中任选一个补充在上面问题中,并加以解答.(注:如果选择多个条件分别解答,按第一个解答计分.)
解:若选①由bsin2A﹣asinAcosC=csin2A及正弦定理可得:
,
A(0,π),,,
所以,
所以,,
因为△ABC的外接圆的面积为3π,由正弦定理可得,,
又△ABC的面积为,所以,即,所以.
由余弦定理得,则,
所以,即,
所以△ABC的周长;
若选②,由正弦定理得,
因为,所以,
由,可得,故,
因为,故,
因此.
其余步骤同①
若选③,由正弦定理可得,,
将,
代入上式可得,,
所以,
因为,所以,即,由于,所以,
其余步骤同①.
19.(本小题满分12分)
如图,四边形ABCD为直角梯形,AB∥CD,AB⊥BC,AB=2BC=2,CD=3BC,E为AB的中点,点F在CD上,且EF∥BC,以EF为折痕把四边形EBCF折起,使二面角B—EF—D为直角,点B,C折起后的位置分别记为点G,H.
(1)求证:AD⊥平面AHF;
(2)在线段HD上存在一点P,使平面PAE与平面AEG所成的二面角的余弦值为,延长GH到点M,使HM=GH,判断直线PM是否在平面PAE中,说明理由.
解:(1)证明:
∴EF⊥CF,即EF⊥HF,
又∵平面EGHF⊥平面AEFD,平面EGHF平面AEFD=EF,
∴HF⊥平面AEFD,∴HF⊥AD,
∵点E为AB的中点,AB=2BC=2,CD=3BC,AB∥CD,EF∥BC,
∴AE=EF=1,DF=2,
∴AF=,AD=,
又HFAF=F,∴AD⊥平面AHF;
(2)由(1)知HF⊥平面AEFD,EF⊥FD,∴HF⊥FD,HF⊥EF,
如图,以F为原点,FE,FD,FH所在直线分别为x轴,y轴,z轴,
建立空间直角坐标系F—xyz,
则E(1,0,0),D(0,2,0),H(0,0,1),A(1,1,0),G(1,0,1)
,
∴
设平面PAE的法向量为,
则,
令,得,
易知平面AEG的一个法向量为
由,解得
∴P为HD中点,
由,得,又,∴,
又平面PAE的一个法向量
,因为点P在平面PAE内,
∴直线PM在平面PAE内.
20.(本小题满分12分)
随着智能手机的普及,手机计步软件迅速流行开来,这类软件能自动记载用户每日健步的步数.某市大型企业为了了解其员工每日健步走的情况,从正常上班的员工中随机抽取了2000人,统计了他们手机计步软件上同一天健步的步数(单位:千步,假设每天健步的步数均在3千步至21千步之间).将样本数据分成[3,5),[5,7),[7,9),[9,11),[11,13),[13,15),[15,17),[17,19),[19,21]九组,绘制成如图所示的频率分布直方图,并用样本的频率分布估计总体的频率分布.
(1)求图中a的值;
(2)设该企业正常上班的员工健步步数(单位:千步)近似服从正态分布N(,),其中近似为样本的平均数(各区间数据用中点值近似计算),取=3.64,若该企业恰有10万正常上班的员工,试估计这些员工中日健步步数Z位于区间[4.88,15.8]范围内的人数;
(3)现从该企业员工中随机抽取20人,其中有k名员工的日健步步数在13千步至15千步内的概率为P(X=k),其中k=0,1,2,…,20,当P(X=k)最大时,求k的值.
参考数据:若随机变量服从正态分布N(,),则P(<≤)≈0.6827,P(<≤)≈0.9545,P(<≤)≈0.9973.
解:(1)由,
解得.
(2)
则(人),所以日健步步数Z位于区间[4.88,15.8]范围内的人数约为8186人;
(3)设从该企业员工中随机抽取20人日健步步数在13千步至15千步的员工有X人,则X~B(20,0.2),
其中有k名员工的概率为
,其中k=0,1,2,…,20,
记,
当时,,则;
当时,,则,
所以当k=4时,最大.
21.(本小题满分12分)
设函数(aR).
(1)讨论函数的单调区间;
(2)若有两个极值点,,记过点A(,),B(,)的直线斜率为k,问:是否存在a,使得k=2﹣a?若存在,求出a的值;若不存在,请说明理由.
解:(1)的定义域为
令,其判别式
上单调递增,
的两根都小于0,在上故在上单调递增,
③当a>2时,,的两根为
上单调递增,上单调递减;
(2)由(1)知,若有两个极值点,,则只能是情况③,故a>2,
因为
所以
又由(1)知,,于是
若存在,使得,则,即
即
再由(1)知,函数在上单调递增,而,
所以
22.(本小题满分12分)
已知P(0,1)为椭圆(a>b>0)上的一点,焦距长为2.PA、PB为椭圆的两条动弦,其倾斜角分别为、,且+=(0<<,0<<).
(1)求椭圆的标准方程;
(2)探究直线AB是否过定点,若过定点,求出定点坐标;若不过定点,请说明理由.
解:(1)由题意知,所以
所以椭圆的标准方程为;
(2)①当直线AB斜率不存在时,设为,设点A坐标为,点B坐标为,
由于
所以
∴,
所以直线AB斜率不存在时,不符合题意;
②当直线AB斜率存在时,设方程为,点A坐标为,点B坐标为
联立,得,
显然,直线,不经过点(0,1),即,
故有,,
化简得,
所以直线AB为
显然当时,上式成立,直线AB过定点(﹣4,﹣3),
综上,直线AB过定点(﹣4,﹣3).
2
同课章节目录
