2021年苏科新版七年级数学下册7.1探索直线平行的条件同步训练1(wordb 附答案)
文档属性
| 名称 | 2021年苏科新版七年级数学下册7.1探索直线平行的条件同步训练1(wordb 附答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 226.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-12 15:47:49 | ||
图片预览



文档简介
2021年苏科新版七年级数学下册7.1探索直线平行的条件同步训练1(附答案)
1.下列说法:①如果∠1+∠2+∠3=180°,那么∠1,∠2,∠3三个角互为补角;②如果∠A+∠B=90°,那么∠A与∠B互为余角;③“对顶角相等”成立,反之“相等的角是对顶角”也成立;④两条直线被第三条直线所截,同位角相等;⑤两点之间,线段最短.正确的个数是( )
A.2个 B.3个 C.4个 D.5个
2.给出下列说法,正确的是( )
A.两条直线被第三条直线所截,同位角相等
B.平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交
C.相等的两个角是对顶角
D.从直线外一点到这条直线的垂线段,叫做这点到直线的距离
3.下列说法正确的有( )
①对顶角相等;②同位角相等;
③若两个角不相等,则这两个角一定不是对顶角;
④若两个角不相等,则这两个角一定不是同位角
A.1个 B.2个 C.3个 D.4个
4.下列说法:(1)两条直线被第三条直线所截,内错角相等;(2)相等的角是对顶角;(3)互余的两个角一定都是直角;(4)互补的两个角一定有钝角,其中正确的有( )
A.0个 B.1个 C.2个 D.3个
5.如图,∠1和∠2是一对( )
A.同位角 B.内错角 C.同旁内角 D.对顶角
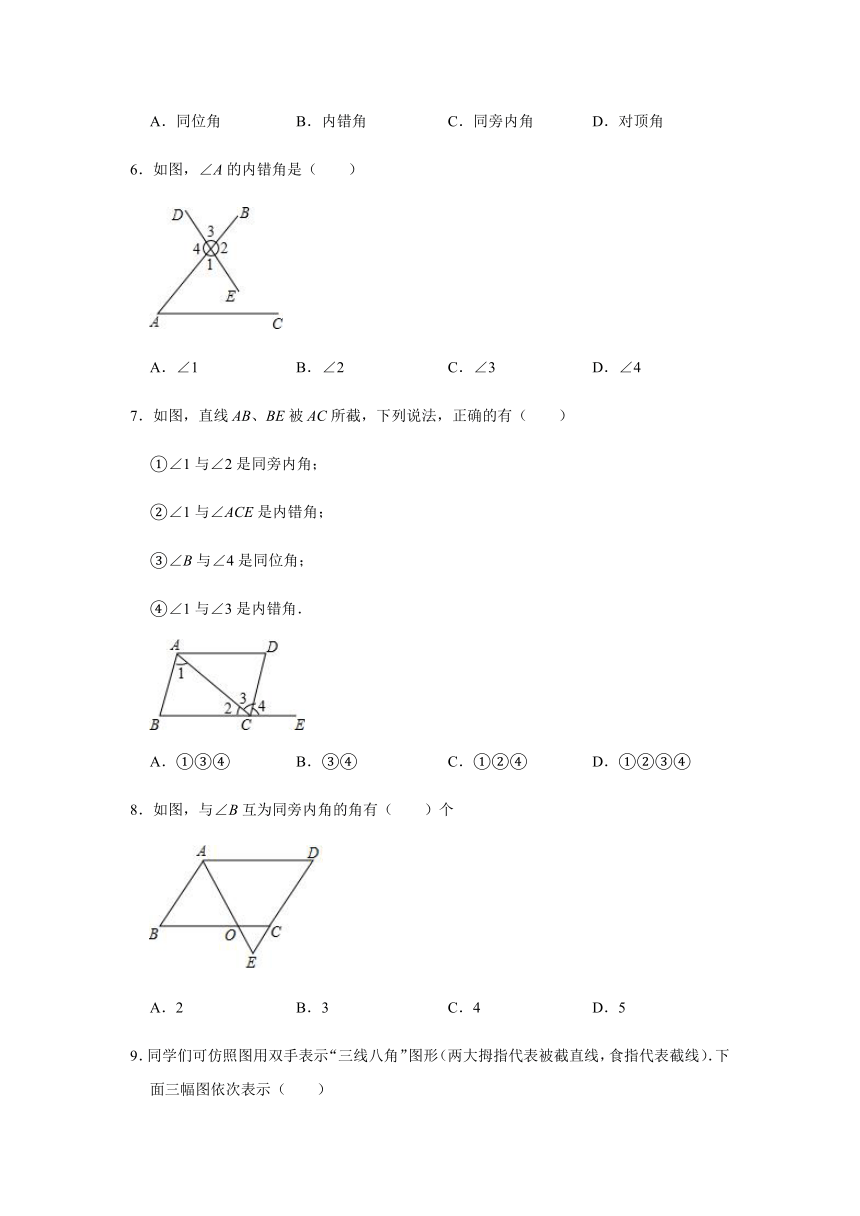
6.如图,∠A的内错角是( )
A.∠1 B.∠2 C.∠3 D.∠4
7.如图,直线AB、BE被AC所截,下列说法,正确的有( )
①∠1与∠2是同旁内角;
②∠1与∠ACE是内错角;
③∠B与∠4是同位角;
④∠1与∠3是内错角.
A.①③④ B.③④ C.①②④ D.①②③④
8.如图,与∠B互为同旁内角的角有( )个
A.2 B.3 C.4 D.5
9.同学们可仿照图用双手表示“三线八角”图形(两大拇指代表被截直线,食指代表截线).下面三幅图依次表示( )
A.同位角、同旁内角、内错角 B.同位角、内错角、同旁内角
C.同位角、对顶角、同旁内角 D.同位角、内错角、对顶角
10.如图所示,下列说法错误的是( )
A.∠A与∠B是同旁内角 B.∠1与∠2是内错角
C.∠A与∠C是内错角 D.∠A与∠1是同位角
11.如图直线AB,CD被EF所截,图中标注的角中为同旁内角的是( )
A.∠1与∠7 B.∠2与∠8 C.∠3与∠5 D.∠4与∠7
12.如图所示,AB是一条直线,若∠1=∠2,则∠3=∠4,其理由是( )
A.内错角相等 B.等角的补角相等
C.同角的补角相等 D.等量代换
13.如图,点E、F分别是AB、CD上的点,点G是BC的延长线上一点,且∠B=∠DCG=∠D,则下列判断不一定成立的是( )
A.AB∥CD B.AD∥BG
C.∠B=∠AEF D.∠BEF+∠EFC=180°
14.如图,在下列给出的条件中,能判定DF∥AB的是( )
A.∠4=∠3 B.∠1=∠A C.∠1=∠4 D.∠4+∠2=180°
15.如图,下列条件能得到BD∥CE的是( )
A.∠1=∠2 B.∠A=∠F C.∠ABD=∠2 D.∠C=∠D
16.如图,分别将木条a,b与木条c钉在一起,若∠1=50°,∠2=80°,要使木条a与b平行,则木条a需要顺时针转动的最小度数为( )
A.30° B.50° C.80° D.130°
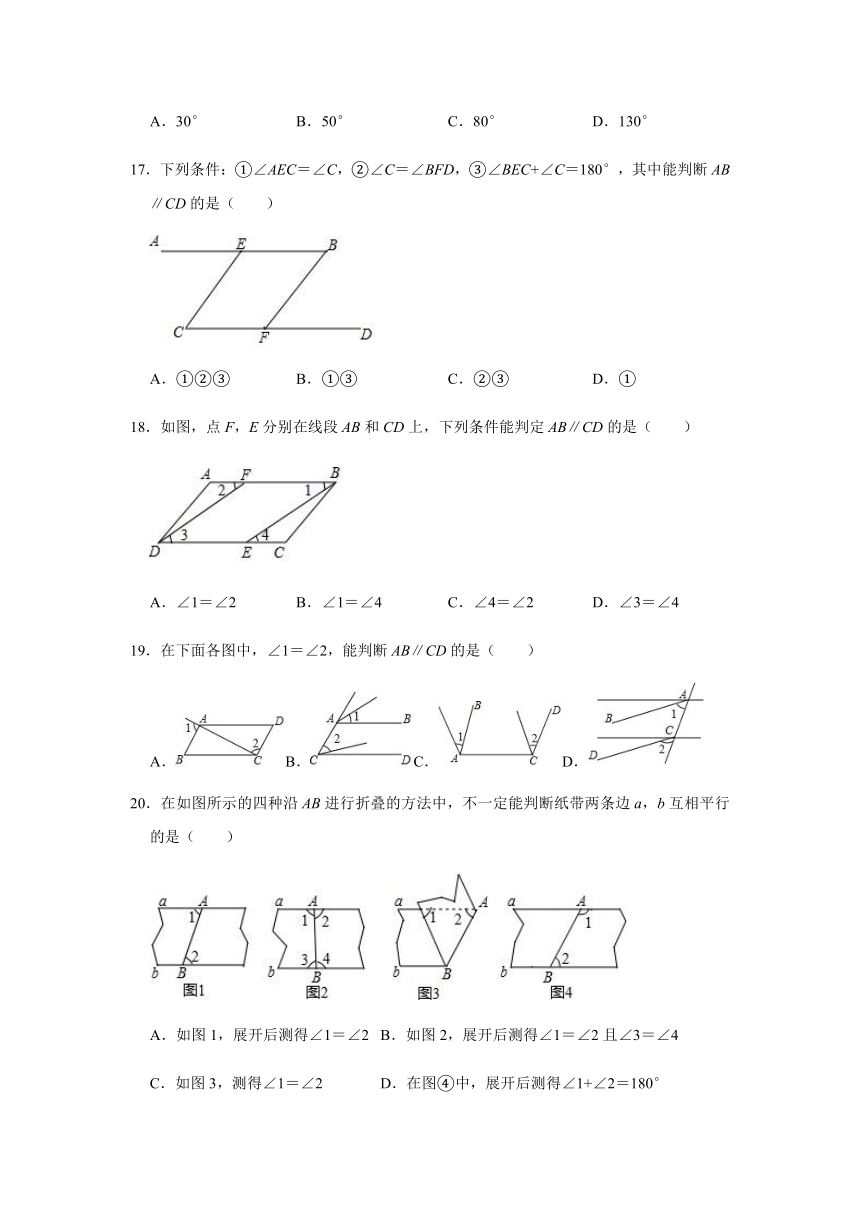
17.下列条件:①∠AEC=∠C,②∠C=∠BFD,③∠BEC+∠C=180°,其中能判断AB∥CD的是( )
A.①②③ B.①③ C.②③ D.①
18.如图,点F,E分别在线段AB和CD上,下列条件能判定AB∥CD的是( )
A.∠1=∠2 B.∠1=∠4 C.∠4=∠2 D.∠3=∠4
19.在下面各图中,∠1=∠2,能判断AB∥CD的是( )
A.B.C.D.
20.在如图所示的四种沿AB进行折叠的方法中,不一定能判断纸带两条边a,b互相平行的是( )
A.如图1,展开后测得∠1=∠2 B.如图2,展开后测得∠1=∠2且∠3=∠4
C.如图3,测得∠1=∠2 D.在图④中,展开后测得∠1+∠2=180°
21.如图,与∠1是同旁内角的是 ,与∠2是内错角的是 .
22.如图,∠A与 是内错角,∠B的同位角是 ,直线AB和CE被直线BC所截得到的同旁内角是 .
23.图中共有 对内错角.
24.对于任意一个三角形,有 对同旁内角.
25.如图,∠1与∠2是 角;∠3与∠4是 角;∠2与∠4是 角.
26.如图填空.
(1)若ED,BC被AB所截,则∠1与 是同位角.
(2)若ED,BC被AF所截,则∠3与 是内错角.
(3)∠1 与∠3是AB和AF被 所截构成的 角.
(4)∠2与∠4是 和 被BC所截构成的 角.
27.如图,如果∠2=100°,那么∠1的同位角等于 度.
28.小明把一副三角板摆放在桌面上,如图所示,其中边BC,DF在同一条直线上,可以得到 ∥ ,依据是 .
29.将一块三角板ABC(∠BAC=90°,∠ABC=30°)按如图方式放置,使A,B两点分别落在直线m,n上.对于给出的四个条件:①∠1=25.5°,∠2=55°30';②∠2=2∠1;③∠1+∠2=90°;④∠ACB=∠1+∠2;⑤∠ABC=∠2﹣∠1.能判断直线m∥n的有 .(填序号)
30.将一副三角板(∠A=30°)按如图所示方式摆放,使得AB∥EF,则∠1等于 度.
31.已知,如图,∠ABC=∠ADC,BF,DE分别平分∠ABC与∠ADC,且∠1=∠3.求证:AB∥DC,请根据条件进行推理,得出结论,并在括号内注明理由.
证明:
∵BF,DE分别平分∠ABC与∠ADC,(已知)
∴∠1=∠ABC,∠2=∠ADC.( )
∵∠ABC=∠ADC,( )
∴∠ =∠ (等量代换)
∵∠1=∠3( )
∴∠2=∠ .( )
∴ ∥ .( )
32.填空:已知:如图,B、C、E三点在同一直线上,A、F、E三点在同一直线上,∠1=∠2=∠E,∠3=∠4.求证:AB∥CD.
证明:∵∠2=∠E
∴ (内错角相等,两直线平?)
∴∠3= (两直线平?,内错角相等)
∵∠3=∠4
∴∠4=∠DAC( )
∵∠1=∠2
∴∠1+∠CAF=∠2+∠CAF,( )
即∠BAF=
∴∠4=∠BAF
∴AB∥CD(同位?相等,两直线平?)
33.如图,已知∠B=30°,∠D=20°,∠BCD=50°,试说明AB∥DE.
34.如图,已知GH、MN分别平分∠AGE、∠DMF,且∠AGH=∠DMN,
试说明AB∥CD的理由.
解:因为GH平分∠AGE(已知),
所以∠AGE=2∠AGH( )
同理∠ =2∠DMN
因为∠AGH=∠DMN(已知)
所以∠AGE=∠ ( )
又因为∠AGE=∠FGB ( )
所以∠ =∠FGB ( )
所以AB∥CD ( ).
35.完成下面的证明:
如图,BE平分∠ABD,DE平分∠BDC,且∠α+∠β=90°,求证:AB∥CD.
证明:∵BE平分∠ABD ( )
∴∠ABD=2∠α ( )
∵DE平分∠BDC(已知)
∵∠BDC= ( )
∴∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β) ( )
∵∠α+∠β=90°(已知)
∴∠ABD+∠BDC=180°( )
∴AB∥CD ( )
36.如图,已知∠A=∠ADE,∠C=∠E.求证:BE∥CD.
参考答案
1.解:①如果∠1+∠2+∠3=180°,那么∠1,∠2,∠3三个角互为补角,是假命题;②如果∠A+∠B=90°,那么∠A与∠B互为余角,是真命题;③“对顶角相等”成立,反之“相等的角是对顶角”也成立,是假命题;④两条直线被第三条直线所截,同位角相等,是假命题;⑤两点之间,线段最短,是真命题;
故选:A.
2.解:A、两条直线被第三条直线所截,同位角不一定相等,故选项错误;
B、平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交,故选项正确;
C、相等的两个角不一定是对顶角,故选项错误;
D、从直线外一点到这条直线的垂线段的长度,叫做这点到直线的距离,故选项错误.
故选:B.
3.解:①对顶角相等,说法正确;
②当两平行线被第三条直线所截时,同位角一定相等,说法错误;
③对顶角一定相等,所以若两个角不相等,则这两个角一定不是对顶角,说法正确;
④若两个角不相等,则这两个角可以同位角,说法错误.
综上所述,正确的说法有2个.
故选:B.
4.解:(1)两条相互平行的直线被第三条直线所截,内错角相等,故说法错误;
(2)对顶角相等,但是相等的角不一定是对顶角,故说法错误;
(3)互余的两个角的和一定都是直角,故说法错误;
(4)互补的两个角有可能是两个直角,故说法错误.
故选:A.
5.解:∠1和∠2是一对内错角,
故选:B.
6.解:∠A的内错角是∠4.
故选:D.
7.解:①∠1与∠2是同旁内角,说法正确;
②∠1与∠ACE是内错角,说法正确;
③∠B与∠4是同位角,说法正确;
④∠1与∠3是内错角说法正确,
故选:D.
8.解:与∠B互为同旁内角的角有∠AOB,∠BAO,∠BCD,∠BAD共4个.
故选:C.
9.解:根据同位角、内错角、同旁内角的概念,可知
第一个图是同位角,第二个图是内错角,第三个图是同旁内角.
故选:B.
10.解:A、∠A与∠B是同旁内角,正确;
B、∠1与∠2是内错角,正确;
C、∠A与∠C是同旁内角,错误;
D、∠A与∠1是同位角,正确;
故选:C.
11.解:A.∠1与∠7不是直线AB,CD被EF所截而成的同旁内角,故本选项错误;
B.∠2与∠8不是直线AB,CD被EF所截而成的同旁内角,故本选项错误;
C.∠3与∠5是直线AB,CD被EF所截而成的同旁内角,故本选项正确;
D.∠4与∠7不是直线AB,CD被EF所截而成的同旁内角,故本选项错误;
故选:C.
12.解:∵∠1=∠2,
∴∠3=∠4(等角的补角相等).
故选:B.
13.解:A、∵∠B=∠DCG=∠D,
∴AB∥DC,AD∥BG,正确,故本选项不符合题意;
B、∵∠B=∠DCG=∠D,
∴AB∥DC,AD∥BG,正确,故本选项不符合题意;
C、根据AB∥DC,AD∥BG不能推出EF∥BC,所以不能推出∠B=∠AEF,错误,故本选项符合题意;
D、∵AB∥CD,
∴∠BEF+∠EFC=180°,正确,故本选项不符合题意;
故选:C.
14.解:A、∵∠4=∠3,∴DE∥AC,不符合题意;
B、∵∠1=∠A,∴DE∥AC,不符合题意;
C、∵∠1=∠3,∴DF∥AB,符合题意;
D、∵∠4+∠2=180°,∴DE∥AC,不符合题意;
故选:C.
15.解:A、如图,∵∠1=∠3,1=∠2,∴∠2=∠3,∴BD∥CE;
B、∠A=∠F,不能判定BD∥CE;
C、∠ABD=∠2,不能判定BD∥CE;
D、∠C=∠D,不能判定BD∥CE.
故选:A.
16.解:如图.
∵∠AOB=∠1=50°时,OA∥b,
∴要使木条a与b平行,木条a需要顺时针转动的最小度数为80°﹣50°=30°.
故选:A.
17.解:①由“内错角相等,两直线平行”知,根据∠AEC=∠C能判断AB∥CD.
②由“同位角角相等,两直线平行”知,根据∠AEC=∠C能判断BF∥EC.
③由“同旁内角互补,两直线平行”知,根据∠AEC=∠C能判断AB∥CD.
故选:B.
18.解:根据∠1=∠2,可得DF∥BE,故A错误;
根据∠1=∠4,可得AB∥CD,故B正确;
根据∠4=∠2,不能判定AB∥CD,故C错误;
根据∠3=∠4,可得DF∥BE,故D错误;
故选:B.
19.解:第一个图中,∠1、∠2不是两条直线被第三条直线所截的内错角或同位角,不能判定AB∥CD;
第二个图中,∠1、∠2不是两条直线被第三条直线所截的同位角,不能判定AB∥CD;
第三个图中,∠1、∠2不是两条直线被第三条直线所截的同位角,不能判定AB∥CD;
第四个图中,∠1、∠2是两条直线被第三条直线所截的同位角,能判定AB∥CD;
故选:D.
20.解:A、当∠1=∠2时,a∥b;
B、由∠1=∠2且∠3=∠4可得∠1=∠2=∠3=∠4=90°,∴a∥b;
C、∠1=∠2不能判定a,b互相平行;
D、由∠1+∠2=180°可知a∥b;
故选:C.
21.解:如图,与∠1是同旁内角的是∠5,与∠2是内错角的是∠3.
故答案为:∠5;∠3.
22.解:如图所示,∠A与∠ACD,∠ACE是内错角,
∠B的同位角是∠ECD,∠ACD,
直线AB和CE被直线BC所截得到的同旁内角是∠B与∠BCE,
故答案为:∠ACD,∠ACE;∠ECD,∠ACD;∠B与∠BCE.
23.解:根据内错角的定义得:
∠EAB与∠ABC,
∠BAC与∠ACD,
∠CBF与∠ACB;
故答案为:3.
24.解:如图所示:
∠A与∠B,∠B与∠C,∠C与∠A都是同旁内角,
故答案为:3.
25.解:由图形可得,∠1与∠2是内错角;∠3与∠4是同位角;∠2与∠4是邻补角.
故答案为:内错、同位、邻补.
26.解:(1)如图:若ED,BC被AB所截,则∠1与∠2是同位角,
(2)若ED,BC被AF所截,则∠3与∠4是内错角,
(3)∠1 与∠3是AB和AF被ED所截构成的内错角,
(4)∠2与∠4是AB和AF被BC所截构成的同位角.
故答案为∠2;∠4;ED,内错;AB,AF,同位.
27.解:如右图所示,
∵∠2+∠3=180°,∠2=100°
∴∠3=80°,
∴∠1的同位角∠3等于80°.
故答案是80°.
28.解:小明把一副三角板摆放在桌面上,如图所示,其中边BC,DF在同一条直线上,可以得到AC∥DE,依据是内错角相等,两直线平行.
故答案为:AC,DE,内错角相等,两直线平行.
29.解:①∵∠1=25.5°+∠ABC=55.5°=∠2=55°30',所以,m∥n;
②没有指明∠1的度数,当∠1≠30°,∠2≠∠1+30°,不能判断直线m∥n,故∠2=2∠1,不能判断直线m∥n;
③∠1+∠2=90°,不能判断直线m∥n;
④∠ACB=∠1+∠2,不能判断直线m∥n;
⑤∠ABC=∠2﹣∠1,判断直线m∥n;
故答案为:①⑤
30.解:∵将一副三角板(∠A=30°)按如图所示方式摆放,使得AB∥EF,
∴∠E=∠EDB=45°,∠B=60°,
∴∠1=45°+60°=105°.
故答案为:105.
31.证明:∵BF,DE分别平分∠ABC与∠ADC,(已知)
∴∠1=∠ABC,∠2=∠ADC.(角平分线的定义)
∵∠ABC=∠ADC,(已知)
∴∠1=∠2,(等量代换)
∵∠1=∠3,(已知)
∴∠2=∠3.(等量代换)
∴AB∥DC.(内错角相等,两直线平行)
故答案为:角平分线的定义;已知;1,2;已知;3,等量代换;AB,DC,内错角相等,两直线平行.
32.证明:∵∠2=∠E,
∴AD∥BC(内错角相等,两直线平行),
∴∠3=∠DAC(两直线平行,内错角相等),
∵∠3=∠4,
∴∠4=∠DAC(等量代换),
∵∠1=∠2
∴∠1+∠CAF=∠2+∠CAF(等式性质),
即∠BAF=∠DAC,
∴∠4=∠BAF,
∴AB∥CD(同位?相等,两直线平行).
故答案为:AD∥BC,∠DAC,等量代换,等式性质,∠DAC.
33.证明:如图,作CM∥AB,则∠B=∠BCM,
∵∠BCD=50°,∠B=30°,
∴∠MCD=50°﹣30°=20°,
∵∠D=20°,
∴∠D=∠MCD,
∴CM∥ED,
∴AB∥DE.
34.解:因为GH平分∠AGE(已知),
所以∠AGE=2∠AGH(角平分线的定义)
同理∠DMF=2∠DMN
因为∠AGH=∠DMN(已知)
所以∠AGE=∠DMF(等量代换)
又因为∠AGE=∠FGB (对顶角相等)
所以∠DMF=∠FGB (等量代换)
所以AB∥CD (同位角相等,两直线平行).
故答案为:角平分线的定义,DMF,DMF,等量代换,对顶角相等,DMF,等量代换,同位角相等,两直线平行.
35.证明:BE平分∠ABD(已知),
∴∠ABD=2∠α(角平分线的定义).
∵DE平分∠BDC(已知),
∴∠BDC=2∠β (角平分线的定义)
∴∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β)(等量代换)
∵∠α+∠β=90°(已知),
∴∠ABD+∠BDC=180°(等量代换).
∴AB∥CD(同旁内角互补,两直线平行).
故答案为:已知,角平分线的定义,2∠β,角平分线的定义,等量代换,等量代换,同旁内角互补两直线平行.
36.证明:∵∠A=∠ADE,
∴DE∥AC,
∴∠ABE=∠E,
又∵∠C=∠E,
∴∠ABE=∠C,
∴BE∥CD
1.下列说法:①如果∠1+∠2+∠3=180°,那么∠1,∠2,∠3三个角互为补角;②如果∠A+∠B=90°,那么∠A与∠B互为余角;③“对顶角相等”成立,反之“相等的角是对顶角”也成立;④两条直线被第三条直线所截,同位角相等;⑤两点之间,线段最短.正确的个数是( )
A.2个 B.3个 C.4个 D.5个
2.给出下列说法,正确的是( )
A.两条直线被第三条直线所截,同位角相等
B.平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交
C.相等的两个角是对顶角
D.从直线外一点到这条直线的垂线段,叫做这点到直线的距离
3.下列说法正确的有( )
①对顶角相等;②同位角相等;
③若两个角不相等,则这两个角一定不是对顶角;
④若两个角不相等,则这两个角一定不是同位角
A.1个 B.2个 C.3个 D.4个
4.下列说法:(1)两条直线被第三条直线所截,内错角相等;(2)相等的角是对顶角;(3)互余的两个角一定都是直角;(4)互补的两个角一定有钝角,其中正确的有( )
A.0个 B.1个 C.2个 D.3个
5.如图,∠1和∠2是一对( )
A.同位角 B.内错角 C.同旁内角 D.对顶角
6.如图,∠A的内错角是( )
A.∠1 B.∠2 C.∠3 D.∠4
7.如图,直线AB、BE被AC所截,下列说法,正确的有( )
①∠1与∠2是同旁内角;
②∠1与∠ACE是内错角;
③∠B与∠4是同位角;
④∠1与∠3是内错角.
A.①③④ B.③④ C.①②④ D.①②③④
8.如图,与∠B互为同旁内角的角有( )个
A.2 B.3 C.4 D.5
9.同学们可仿照图用双手表示“三线八角”图形(两大拇指代表被截直线,食指代表截线).下面三幅图依次表示( )
A.同位角、同旁内角、内错角 B.同位角、内错角、同旁内角
C.同位角、对顶角、同旁内角 D.同位角、内错角、对顶角
10.如图所示,下列说法错误的是( )
A.∠A与∠B是同旁内角 B.∠1与∠2是内错角
C.∠A与∠C是内错角 D.∠A与∠1是同位角
11.如图直线AB,CD被EF所截,图中标注的角中为同旁内角的是( )
A.∠1与∠7 B.∠2与∠8 C.∠3与∠5 D.∠4与∠7
12.如图所示,AB是一条直线,若∠1=∠2,则∠3=∠4,其理由是( )
A.内错角相等 B.等角的补角相等
C.同角的补角相等 D.等量代换
13.如图,点E、F分别是AB、CD上的点,点G是BC的延长线上一点,且∠B=∠DCG=∠D,则下列判断不一定成立的是( )
A.AB∥CD B.AD∥BG
C.∠B=∠AEF D.∠BEF+∠EFC=180°
14.如图,在下列给出的条件中,能判定DF∥AB的是( )
A.∠4=∠3 B.∠1=∠A C.∠1=∠4 D.∠4+∠2=180°
15.如图,下列条件能得到BD∥CE的是( )
A.∠1=∠2 B.∠A=∠F C.∠ABD=∠2 D.∠C=∠D
16.如图,分别将木条a,b与木条c钉在一起,若∠1=50°,∠2=80°,要使木条a与b平行,则木条a需要顺时针转动的最小度数为( )
A.30° B.50° C.80° D.130°
17.下列条件:①∠AEC=∠C,②∠C=∠BFD,③∠BEC+∠C=180°,其中能判断AB∥CD的是( )
A.①②③ B.①③ C.②③ D.①
18.如图,点F,E分别在线段AB和CD上,下列条件能判定AB∥CD的是( )
A.∠1=∠2 B.∠1=∠4 C.∠4=∠2 D.∠3=∠4
19.在下面各图中,∠1=∠2,能判断AB∥CD的是( )
A.B.C.D.
20.在如图所示的四种沿AB进行折叠的方法中,不一定能判断纸带两条边a,b互相平行的是( )
A.如图1,展开后测得∠1=∠2 B.如图2,展开后测得∠1=∠2且∠3=∠4
C.如图3,测得∠1=∠2 D.在图④中,展开后测得∠1+∠2=180°
21.如图,与∠1是同旁内角的是 ,与∠2是内错角的是 .
22.如图,∠A与 是内错角,∠B的同位角是 ,直线AB和CE被直线BC所截得到的同旁内角是 .
23.图中共有 对内错角.
24.对于任意一个三角形,有 对同旁内角.
25.如图,∠1与∠2是 角;∠3与∠4是 角;∠2与∠4是 角.
26.如图填空.
(1)若ED,BC被AB所截,则∠1与 是同位角.
(2)若ED,BC被AF所截,则∠3与 是内错角.
(3)∠1 与∠3是AB和AF被 所截构成的 角.
(4)∠2与∠4是 和 被BC所截构成的 角.
27.如图,如果∠2=100°,那么∠1的同位角等于 度.
28.小明把一副三角板摆放在桌面上,如图所示,其中边BC,DF在同一条直线上,可以得到 ∥ ,依据是 .
29.将一块三角板ABC(∠BAC=90°,∠ABC=30°)按如图方式放置,使A,B两点分别落在直线m,n上.对于给出的四个条件:①∠1=25.5°,∠2=55°30';②∠2=2∠1;③∠1+∠2=90°;④∠ACB=∠1+∠2;⑤∠ABC=∠2﹣∠1.能判断直线m∥n的有 .(填序号)
30.将一副三角板(∠A=30°)按如图所示方式摆放,使得AB∥EF,则∠1等于 度.
31.已知,如图,∠ABC=∠ADC,BF,DE分别平分∠ABC与∠ADC,且∠1=∠3.求证:AB∥DC,请根据条件进行推理,得出结论,并在括号内注明理由.
证明:
∵BF,DE分别平分∠ABC与∠ADC,(已知)
∴∠1=∠ABC,∠2=∠ADC.( )
∵∠ABC=∠ADC,( )
∴∠ =∠ (等量代换)
∵∠1=∠3( )
∴∠2=∠ .( )
∴ ∥ .( )
32.填空:已知:如图,B、C、E三点在同一直线上,A、F、E三点在同一直线上,∠1=∠2=∠E,∠3=∠4.求证:AB∥CD.
证明:∵∠2=∠E
∴ (内错角相等,两直线平?)
∴∠3= (两直线平?,内错角相等)
∵∠3=∠4
∴∠4=∠DAC( )
∵∠1=∠2
∴∠1+∠CAF=∠2+∠CAF,( )
即∠BAF=
∴∠4=∠BAF
∴AB∥CD(同位?相等,两直线平?)
33.如图,已知∠B=30°,∠D=20°,∠BCD=50°,试说明AB∥DE.
34.如图,已知GH、MN分别平分∠AGE、∠DMF,且∠AGH=∠DMN,
试说明AB∥CD的理由.
解:因为GH平分∠AGE(已知),
所以∠AGE=2∠AGH( )
同理∠ =2∠DMN
因为∠AGH=∠DMN(已知)
所以∠AGE=∠ ( )
又因为∠AGE=∠FGB ( )
所以∠ =∠FGB ( )
所以AB∥CD ( ).
35.完成下面的证明:
如图,BE平分∠ABD,DE平分∠BDC,且∠α+∠β=90°,求证:AB∥CD.
证明:∵BE平分∠ABD ( )
∴∠ABD=2∠α ( )
∵DE平分∠BDC(已知)
∵∠BDC= ( )
∴∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β) ( )
∵∠α+∠β=90°(已知)
∴∠ABD+∠BDC=180°( )
∴AB∥CD ( )
36.如图,已知∠A=∠ADE,∠C=∠E.求证:BE∥CD.
参考答案
1.解:①如果∠1+∠2+∠3=180°,那么∠1,∠2,∠3三个角互为补角,是假命题;②如果∠A+∠B=90°,那么∠A与∠B互为余角,是真命题;③“对顶角相等”成立,反之“相等的角是对顶角”也成立,是假命题;④两条直线被第三条直线所截,同位角相等,是假命题;⑤两点之间,线段最短,是真命题;
故选:A.
2.解:A、两条直线被第三条直线所截,同位角不一定相等,故选项错误;
B、平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交,故选项正确;
C、相等的两个角不一定是对顶角,故选项错误;
D、从直线外一点到这条直线的垂线段的长度,叫做这点到直线的距离,故选项错误.
故选:B.
3.解:①对顶角相等,说法正确;
②当两平行线被第三条直线所截时,同位角一定相等,说法错误;
③对顶角一定相等,所以若两个角不相等,则这两个角一定不是对顶角,说法正确;
④若两个角不相等,则这两个角可以同位角,说法错误.
综上所述,正确的说法有2个.
故选:B.
4.解:(1)两条相互平行的直线被第三条直线所截,内错角相等,故说法错误;
(2)对顶角相等,但是相等的角不一定是对顶角,故说法错误;
(3)互余的两个角的和一定都是直角,故说法错误;
(4)互补的两个角有可能是两个直角,故说法错误.
故选:A.
5.解:∠1和∠2是一对内错角,
故选:B.
6.解:∠A的内错角是∠4.
故选:D.
7.解:①∠1与∠2是同旁内角,说法正确;
②∠1与∠ACE是内错角,说法正确;
③∠B与∠4是同位角,说法正确;
④∠1与∠3是内错角说法正确,
故选:D.
8.解:与∠B互为同旁内角的角有∠AOB,∠BAO,∠BCD,∠BAD共4个.
故选:C.
9.解:根据同位角、内错角、同旁内角的概念,可知
第一个图是同位角,第二个图是内错角,第三个图是同旁内角.
故选:B.
10.解:A、∠A与∠B是同旁内角,正确;
B、∠1与∠2是内错角,正确;
C、∠A与∠C是同旁内角,错误;
D、∠A与∠1是同位角,正确;
故选:C.
11.解:A.∠1与∠7不是直线AB,CD被EF所截而成的同旁内角,故本选项错误;
B.∠2与∠8不是直线AB,CD被EF所截而成的同旁内角,故本选项错误;
C.∠3与∠5是直线AB,CD被EF所截而成的同旁内角,故本选项正确;
D.∠4与∠7不是直线AB,CD被EF所截而成的同旁内角,故本选项错误;
故选:C.
12.解:∵∠1=∠2,
∴∠3=∠4(等角的补角相等).
故选:B.
13.解:A、∵∠B=∠DCG=∠D,
∴AB∥DC,AD∥BG,正确,故本选项不符合题意;
B、∵∠B=∠DCG=∠D,
∴AB∥DC,AD∥BG,正确,故本选项不符合题意;
C、根据AB∥DC,AD∥BG不能推出EF∥BC,所以不能推出∠B=∠AEF,错误,故本选项符合题意;
D、∵AB∥CD,
∴∠BEF+∠EFC=180°,正确,故本选项不符合题意;
故选:C.
14.解:A、∵∠4=∠3,∴DE∥AC,不符合题意;
B、∵∠1=∠A,∴DE∥AC,不符合题意;
C、∵∠1=∠3,∴DF∥AB,符合题意;
D、∵∠4+∠2=180°,∴DE∥AC,不符合题意;
故选:C.
15.解:A、如图,∵∠1=∠3,1=∠2,∴∠2=∠3,∴BD∥CE;
B、∠A=∠F,不能判定BD∥CE;
C、∠ABD=∠2,不能判定BD∥CE;
D、∠C=∠D,不能判定BD∥CE.
故选:A.
16.解:如图.
∵∠AOB=∠1=50°时,OA∥b,
∴要使木条a与b平行,木条a需要顺时针转动的最小度数为80°﹣50°=30°.
故选:A.
17.解:①由“内错角相等,两直线平行”知,根据∠AEC=∠C能判断AB∥CD.
②由“同位角角相等,两直线平行”知,根据∠AEC=∠C能判断BF∥EC.
③由“同旁内角互补,两直线平行”知,根据∠AEC=∠C能判断AB∥CD.
故选:B.
18.解:根据∠1=∠2,可得DF∥BE,故A错误;
根据∠1=∠4,可得AB∥CD,故B正确;
根据∠4=∠2,不能判定AB∥CD,故C错误;
根据∠3=∠4,可得DF∥BE,故D错误;
故选:B.
19.解:第一个图中,∠1、∠2不是两条直线被第三条直线所截的内错角或同位角,不能判定AB∥CD;
第二个图中,∠1、∠2不是两条直线被第三条直线所截的同位角,不能判定AB∥CD;
第三个图中,∠1、∠2不是两条直线被第三条直线所截的同位角,不能判定AB∥CD;
第四个图中,∠1、∠2是两条直线被第三条直线所截的同位角,能判定AB∥CD;
故选:D.
20.解:A、当∠1=∠2时,a∥b;
B、由∠1=∠2且∠3=∠4可得∠1=∠2=∠3=∠4=90°,∴a∥b;
C、∠1=∠2不能判定a,b互相平行;
D、由∠1+∠2=180°可知a∥b;
故选:C.
21.解:如图,与∠1是同旁内角的是∠5,与∠2是内错角的是∠3.
故答案为:∠5;∠3.
22.解:如图所示,∠A与∠ACD,∠ACE是内错角,
∠B的同位角是∠ECD,∠ACD,
直线AB和CE被直线BC所截得到的同旁内角是∠B与∠BCE,
故答案为:∠ACD,∠ACE;∠ECD,∠ACD;∠B与∠BCE.
23.解:根据内错角的定义得:
∠EAB与∠ABC,
∠BAC与∠ACD,
∠CBF与∠ACB;
故答案为:3.
24.解:如图所示:
∠A与∠B,∠B与∠C,∠C与∠A都是同旁内角,
故答案为:3.
25.解:由图形可得,∠1与∠2是内错角;∠3与∠4是同位角;∠2与∠4是邻补角.
故答案为:内错、同位、邻补.
26.解:(1)如图:若ED,BC被AB所截,则∠1与∠2是同位角,
(2)若ED,BC被AF所截,则∠3与∠4是内错角,
(3)∠1 与∠3是AB和AF被ED所截构成的内错角,
(4)∠2与∠4是AB和AF被BC所截构成的同位角.
故答案为∠2;∠4;ED,内错;AB,AF,同位.
27.解:如右图所示,
∵∠2+∠3=180°,∠2=100°
∴∠3=80°,
∴∠1的同位角∠3等于80°.
故答案是80°.
28.解:小明把一副三角板摆放在桌面上,如图所示,其中边BC,DF在同一条直线上,可以得到AC∥DE,依据是内错角相等,两直线平行.
故答案为:AC,DE,内错角相等,两直线平行.
29.解:①∵∠1=25.5°+∠ABC=55.5°=∠2=55°30',所以,m∥n;
②没有指明∠1的度数,当∠1≠30°,∠2≠∠1+30°,不能判断直线m∥n,故∠2=2∠1,不能判断直线m∥n;
③∠1+∠2=90°,不能判断直线m∥n;
④∠ACB=∠1+∠2,不能判断直线m∥n;
⑤∠ABC=∠2﹣∠1,判断直线m∥n;
故答案为:①⑤
30.解:∵将一副三角板(∠A=30°)按如图所示方式摆放,使得AB∥EF,
∴∠E=∠EDB=45°,∠B=60°,
∴∠1=45°+60°=105°.
故答案为:105.
31.证明:∵BF,DE分别平分∠ABC与∠ADC,(已知)
∴∠1=∠ABC,∠2=∠ADC.(角平分线的定义)
∵∠ABC=∠ADC,(已知)
∴∠1=∠2,(等量代换)
∵∠1=∠3,(已知)
∴∠2=∠3.(等量代换)
∴AB∥DC.(内错角相等,两直线平行)
故答案为:角平分线的定义;已知;1,2;已知;3,等量代换;AB,DC,内错角相等,两直线平行.
32.证明:∵∠2=∠E,
∴AD∥BC(内错角相等,两直线平行),
∴∠3=∠DAC(两直线平行,内错角相等),
∵∠3=∠4,
∴∠4=∠DAC(等量代换),
∵∠1=∠2
∴∠1+∠CAF=∠2+∠CAF(等式性质),
即∠BAF=∠DAC,
∴∠4=∠BAF,
∴AB∥CD(同位?相等,两直线平行).
故答案为:AD∥BC,∠DAC,等量代换,等式性质,∠DAC.
33.证明:如图,作CM∥AB,则∠B=∠BCM,
∵∠BCD=50°,∠B=30°,
∴∠MCD=50°﹣30°=20°,
∵∠D=20°,
∴∠D=∠MCD,
∴CM∥ED,
∴AB∥DE.
34.解:因为GH平分∠AGE(已知),
所以∠AGE=2∠AGH(角平分线的定义)
同理∠DMF=2∠DMN
因为∠AGH=∠DMN(已知)
所以∠AGE=∠DMF(等量代换)
又因为∠AGE=∠FGB (对顶角相等)
所以∠DMF=∠FGB (等量代换)
所以AB∥CD (同位角相等,两直线平行).
故答案为:角平分线的定义,DMF,DMF,等量代换,对顶角相等,DMF,等量代换,同位角相等,两直线平行.
35.证明:BE平分∠ABD(已知),
∴∠ABD=2∠α(角平分线的定义).
∵DE平分∠BDC(已知),
∴∠BDC=2∠β (角平分线的定义)
∴∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β)(等量代换)
∵∠α+∠β=90°(已知),
∴∠ABD+∠BDC=180°(等量代换).
∴AB∥CD(同旁内角互补,两直线平行).
故答案为:已知,角平分线的定义,2∠β,角平分线的定义,等量代换,等量代换,同旁内角互补两直线平行.
36.证明:∵∠A=∠ADE,
∴DE∥AC,
∴∠ABE=∠E,
又∵∠C=∠E,
∴∠ABE=∠C,
∴BE∥CD
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
