2020-2021学年苏教版小学六年级数学下册《第6章 正比例和反比例》单元测试题(有答案)
文档属性
| 名称 | 2020-2021学年苏教版小学六年级数学下册《第6章 正比例和反比例》单元测试题(有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 170.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-13 00:00:00 | ||
图片预览




文档简介
2020-2021学年苏教版小学六年级数学下册《第6章
正比例和反比例》单元测试题
一.选择题(共10小题)
1.表示x和y成正比例关系的式子是( )
A.x+y=10
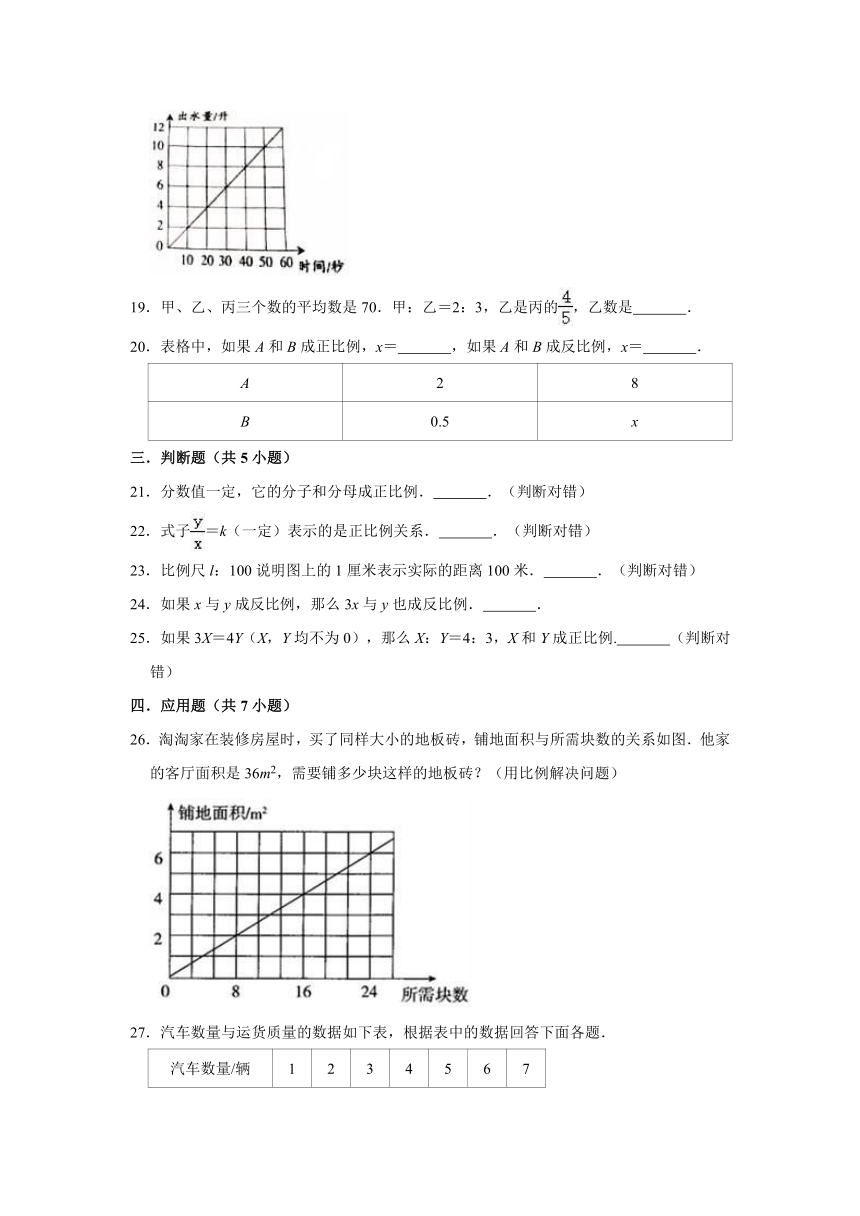
B.x﹣y=10
C.y=10x
2.正方形的边长和它的周长( )
A.成正比例
B.成反比例
C.不成比例
3.下列几种量中,不是成反比例的量是( )
A.路程一定,速度和时间
B.减数一定,被减数和差
C.面积一定,平行四边形的底和高
4.如果A×=B×,(A、B均不为0),那么A( )B.
A.大于
B.小于
C.等于
5.下面x和y成正比例关系的是( )
A.=y
B.3x=4y
C.y=x﹣3
D.=5+
6.下面表格中,如果x和y成正比例关系,那么空格里的数是( )
x
8
40
y
20
A.16
B.100
C.52
D.4
7.下面选项中,两种量成反比例关系的是( )
A.三角形的面积一定,它的高和底
B.汽车的速度一定,行驶的时间和路程
C.一个商场营业时间一定,每天接待顾客的数量和营业额
D.修建一条路的总长度一定,已修的长度和未修的长度
8.用70m长的栅栏靠墙围成一块长方形果园(如图),长与宽的比是4:3,这块长方形果园的面积是( )m2.
A.1200
B.300
C.588
D.294
9.总价一定,单价和数量( )
A.成正比例
B.成反比例
C.不成比例
D.以上都不对
10.=y,且x和y都不为0,当k一定时,x和y( )
A.成正比例
B.成反比例
C.不成比例
D.无法确定
二.填空题(共10小题)
11.王飞以每小时40千米的速度行了240千米,按原路返回时每小时行60千米,王飞往返的平均速度是每小时行
千米.
12.A、B、C三量的关系时A×B=C中,当C一定时,A和B成
关系.
13.三角形的面积一定,底与高成
比例关系.
14.=c,且b≠0,若a一定,b和c成
比例;若b一定,a和c成
比例.
15.当
一定时,
和
成正比例:当
一定时,
和
成反比例.
16.x和y都不为0.如果y=x,那么x和y成
比例:如果=,那么x和y成
比例.
17.在ab=c(a、b、c均不为0)中,当b一定时,a和c成
比例;当c一定时,a和b成
比例.
18.如图是一个水龙头打开后出水量的情况统计.
(1)看图填写下表:
时间(秒)
20
出水量(升)
8
(2)这个水龙头打开的时间和出水量成
比例,算一算
秒时出水量是9.6升.
(3)20秒的出水量比50秒的出水量少
%.
19.甲、乙、丙三个数的平均数是70.甲:乙=2:3,乙是丙的,乙数是
.
20.表格中,如果A和B成正比例,x=
,如果A和B成反比例,x=
.
A
2
8
B
0.5
x
三.判断题(共5小题)
21.分数值一定,它的分子和分母成正比例.
.(判断对错)
22.式子=k(一定)表示的是正比例关系.
.(判断对错)
23.比例尺l:100说明图上的1厘米表示实际的距离100米.
.(判断对错)
24.如果x与y成反比例,那么3x与y也成反比例.
.
25.如果3X=4Y(X,Y均不为0),那么X:Y=4:3,X和Y成正比例.
(判断对错)
四.应用题(共7小题)
26.淘淘家在装修房屋时,买了同样大小的地板砖,铺地面积与所需块数的关系如图.他家的客厅面积是36m2,需要铺多少块这样的地板砖?(用比例解决问题)
27.汽车数量与运货质量的数据如下表,根据表中的数据回答下面各题.
汽车数量/辆
1
2
3
4
5
6
7
运货质量/吨
4
8
12
16
20
24
28
(1)表中
和
是两种相关联的量,
随着
的变化而变化.
(2)写出几组这两种量中相对应的两个数的比,求出比值,并比较比值的大小.
(3)上面求出的比值表示的意义是什么?
(4)表中相关联的两种量成正比例吗?为什么?
28.图表示了矿泉水的数量与总价的关系,看图回答问题.
①5瓶的总价是
元.
②12瓶的总价是
元.
③
瓶的总价是36元.
29.组装一批电动车,每天组装的辆数和需要的天数如表.
每天组装辆数
20
15
10
需要的天数
12
15
(1)请把上表补充完整.
(2)每天组装的辆数和需要的天数成什么比例?为什么?
(3)如果每天组装30辆,需要组装多少天?如果打算4天完成组装任务,每天需要组装多少辆?
30.一艘轮船从甲港开到乙港,3时行驶了75km.从乙港开到丙港,5时行驶了125km.
(1)分别求轮船从甲港开到乙港,从乙港开到丙港的速度.
(2)轮船行驶的路程和所用时间成什么比例?
(3)用等式把题目里的数量关系表示出来.
31.农业基地里的樱桃树比苹果树少350棵,樱桃树与苹果树的棵数比是3:5,基地里的樱桃树和苹果树各有多少棵?
32.六年级三个班的学生共植树420棵。甲班植的棵数是总数的40%,乙、丙两班植的棵数的比为11:10。三个班各植树多少棵?
参考答案与试题解析
一.选择题(共10小题)
1.解:A.x+y=10,x与y的和一定,不符合正比例的意义;
B.y﹣x=10,x与y的差一定,不符合正比例的意义;
C.由y=10x得=,所以x、y比值一定,x与y成正比例,符合题意;
故选:C.
2.解:正方形的周长÷边长=4(一定),是比值一定,所以正方形的周长和它的边长成正比例;
故选:A.
3.解:A选项:速度×时间=路程(一定),速度和时间乘积一定,成反比例;
B选项:被减数﹣差=被减数(一定),被减数和差是和与差的关系,乘积和比值都不是一定的,不成任何比例;
C选项:平行四边形的底×高=面积(一定),平行四边形的底和高的乘积一定,成反比例关系.
故选:B。
4.解:A×=B×,
因为<,
所以A>B.
故选:A.
5.解:A、xy=3,x和y成反比例;
B、x÷y=,x和y成正比例;
C、y﹣x=﹣3,x和y不成比例;
D、2x=40+y,2x﹣y=40,x和y不成比例.
故选:B.
6.解:y:x=20:8=2.5;
所以,y=40×2.5=100.
x
8
40
y
20
100
故选:B.
7.解:A、因为底×高=面积×2(一定),乘积一定,所以三角形的面积一定,它的底和高成反比例;
B、因为路程÷时间=速度(一定),比值一定,所以行驶的时间和路程成正比例;
C、商场营业时间一定,每天接待顾客的数量和营业额不成比例;
D、已修长度+未修长度=总长度(一定),和一定,所以已修的长度和未修的长度不成比例.
故选:A.
8.解:(70×)×(70×)
=(70×)×(70×)
=28×21
=588(平方米)
答:这块长方形果园的面积是588m2.
故选:C.
9.解:从题中可以得到以下数量关系:
单价×数量=总价(一定),
可以看出,单价和数量是两种相关联的量,单价随数量的变化而变化.总价一定,也就是单价与数量相对应数的乘积一定,符合反比例的意义.所以单价与数量成反比例关系.
故选:B。
10.解:因为=y
所以xy=k+5(一定)
(k一定,所以k+5也是一定的)
x和y的积是定值,
所以x和y成反比例关系,
故选:B。
二.填空题(共10小题)
11.解:240÷60=4(小时);
240×2÷(240÷40+4);
=480÷(6+4);
=480÷10;
=48(千米);
答:王飞往返的平均速度是每小时行48千米.
12.解:(1)C÷A=B(一定),是比值一定,A和C成正比例;
(2)A×B=C(一定),是乘积一定,A和B成反比例.
故答案为:正比例,反比例.
13.解:因为,S=ah×,面积一定,所以底与高成反比例关系.
故答案为:反.
14.解:因为=c,所以b×c=a(一定),是乘积一定,b和c就成反比例;
因为=c,所以a÷c=b(一定),是比值一定,a和c就成正比例.
故答案为:反,正.
15.解:以“单价、数量、总量”之间的数量关系为例分析解答.
①总价:数量=单价(一定),
可以看出,总价和数量是两种相关联的量,总价随数量的变化而变化.单价一定,也就是总价与数量相对应数的比值一定.所以总价与数量成正比例.
②单价×数量=总价(一定),
可以看出,单价和数量是两种相关联的量,单价随数量的变化而变化.总价一定,也就是单价与数量相对应数的乘积一定.所以单价与数量成反比例关系.
故答案为:单价,总价,数量,总价,单价,数量(也可以是其它数量关系中的量).
16.解:x和y都不为0.如果y=x,则:
y÷x=(一定),比值一定,符合正比例的含义,所以x和y成正比例;
如果=,
符合正比例的意义,则xy=3×5=15(一定),乘积一定,所以x和y成
反比例.
故答案为:正,反.
17.解:因为ab=c,即c:a=b(一定),比值一定,所以a和c成正比例;
因为ab=c(一定),乘积一定,所以a和b成反比例;
故答案为:正、反.
18.解:(1)统计表见下图:
时间/秒
20
40
出水量/升
4
8
(2)因为20:4=40:8=5(一定),
是这个水龙头的出水量和打开的时间的比值一定,
符合正比例的意义,所以这个水龙头打开的时间和出水量成成正比例.
每秒的出水量:2÷10=0.2(升),
9.6÷0.2=48(秒).
(3)0.2×20=4(升),0.2×50=10(升)
10﹣4=6(升),6÷10×100%=60%
故答案为:4,8,正,48,60.
19.解:甲:乙=2:3
3×甲=2×乙,
甲=乙;
因为:乙是丙的,
所以:乙:丙=4:5,
丙=乙;
甲:乙:丙=乙:乙:乙
甲:乙:丙=8:12:15;
8+12+15=35(份),
70×3×
=210×,
=72.
答:乙数是72.
20.解:如果A和B成正比例,那么=,根据比例的基本性质,求出x=2;
如果A和B成反比例,那么2×0.5=8x,求出x=0.125.
故答案为:2,0.125.
三.判断题(共5小题)
21.解:=分数值(一定),是比值一定,分子和分母成正比例.
故判断为:正确.
22.解:因为=k(一定),所以这是表示x、y成正比例的式子.
故答案为:√.
23.解:比例尺l:100说明图上的1厘米表示实际的距离100厘米.
故答案为:×
24.解:x
与y成反比例,说明x×y=k,k一定,
3x×y=3k,3是一个常数,所以,3k一定,故3x和y也成比例;
故答案为:√.
25.解:因为3X=4Y(X,Y均不为0),
所以X:Y=4:3=(一定),
符合正比例的意义,所以X与Y成正比例。
故答案为:√。
四.应用题(共7小题)
26.解:根据题意与分析可得:铺地面积与所需块数成正比例关系;
设需要铺x块这样的地板砖,根据题意,可得:
36:x=2:8
2x=36×8
2x÷2=36×8÷2
x=144
答:需要铺144块这样的地板砖.
27.解:(1)表中有汽车数量和运货质量两种量,它们是两种相关联的量,一个量变大,另一个量也随着变大,它们的比值一定,所以汽车数量和运货质量成正比例关系.
(2)4:1=4,8:2=4,12:3=4,16:4=4,它们的比值相等.
(3)根据题意可知,这个比值表示每辆汽车的运货质量.
(4)相关联的两种量成正比例,因为它们的比值一定.
故答案为:汽车数量;运货质量;运货质量;汽车数量.
28.解:(1)5瓶的售价是10元.
(2)10÷5×12
=2×12
=24(元);
答:12瓶的售价是
24元.
(3)36÷(10÷5)
=36÷2
=18(瓶);
答:18瓶的售价是36元.
故答案为:10,24,18.
29.解:(1)15×12=180(辆)
180÷20=9(天)
180÷15=12(辆)
180÷10=18(天)
每天组装辆数
20
15
12
10
需要的天数
9
12
15
18
(2)因为每天组装辆数×需要的天数=180辆(一定),即乘积一定.所以每天组装的辆数和需要的天数成反比例.
(3)180÷30=6(天)
180÷4=45(辆)
答:每天组装30辆,需要组装6天;打算4天完成组装任务,每天需要组装45辆.
故答案为:12,9,18.
30.解:从甲港开到乙港的速度:75÷3=25(千米/时).
从乙港开到丙港的速度:125÷5=25(千米/时).
答:轮船从甲港开到乙港,从乙港开到丙港的速度都是25千米/时.
(2)由(1)可知=25(一定),是比值一定,所以轮船行驶的路程和所用时间成正比例.
(3)设s表示路程,t表示时间,v表示速度,则等量关系为:=v.
31.解:350÷(5﹣3)
=350÷2
=175(棵)
175×3=525(棵)
175×5=875(棵)
答:基地里的樱桃树525棵,苹果树875棵。
32.解:420×40%=168(棵)
(420﹣168)÷(11+10)
=252÷21
=12(棵)
12×11=132(棵)
12×10=120(棵)
答:甲班植树168棵,乙班植树132棵,丙班植树120棵。
正比例和反比例》单元测试题
一.选择题(共10小题)
1.表示x和y成正比例关系的式子是( )
A.x+y=10
B.x﹣y=10
C.y=10x
2.正方形的边长和它的周长( )
A.成正比例
B.成反比例
C.不成比例
3.下列几种量中,不是成反比例的量是( )
A.路程一定,速度和时间
B.减数一定,被减数和差
C.面积一定,平行四边形的底和高
4.如果A×=B×,(A、B均不为0),那么A( )B.
A.大于
B.小于
C.等于
5.下面x和y成正比例关系的是( )
A.=y
B.3x=4y
C.y=x﹣3
D.=5+
6.下面表格中,如果x和y成正比例关系,那么空格里的数是( )
x
8
40
y
20
A.16
B.100
C.52
D.4
7.下面选项中,两种量成反比例关系的是( )
A.三角形的面积一定,它的高和底
B.汽车的速度一定,行驶的时间和路程
C.一个商场营业时间一定,每天接待顾客的数量和营业额
D.修建一条路的总长度一定,已修的长度和未修的长度
8.用70m长的栅栏靠墙围成一块长方形果园(如图),长与宽的比是4:3,这块长方形果园的面积是( )m2.
A.1200
B.300
C.588
D.294
9.总价一定,单价和数量( )
A.成正比例
B.成反比例
C.不成比例
D.以上都不对
10.=y,且x和y都不为0,当k一定时,x和y( )
A.成正比例
B.成反比例
C.不成比例
D.无法确定
二.填空题(共10小题)
11.王飞以每小时40千米的速度行了240千米,按原路返回时每小时行60千米,王飞往返的平均速度是每小时行
千米.
12.A、B、C三量的关系时A×B=C中,当C一定时,A和B成
关系.
13.三角形的面积一定,底与高成
比例关系.
14.=c,且b≠0,若a一定,b和c成
比例;若b一定,a和c成
比例.
15.当
一定时,
和
成正比例:当
一定时,
和
成反比例.
16.x和y都不为0.如果y=x,那么x和y成
比例:如果=,那么x和y成
比例.
17.在ab=c(a、b、c均不为0)中,当b一定时,a和c成
比例;当c一定时,a和b成
比例.
18.如图是一个水龙头打开后出水量的情况统计.
(1)看图填写下表:
时间(秒)
20
出水量(升)
8
(2)这个水龙头打开的时间和出水量成
比例,算一算
秒时出水量是9.6升.
(3)20秒的出水量比50秒的出水量少
%.
19.甲、乙、丙三个数的平均数是70.甲:乙=2:3,乙是丙的,乙数是
.
20.表格中,如果A和B成正比例,x=
,如果A和B成反比例,x=
.
A
2
8
B
0.5
x
三.判断题(共5小题)
21.分数值一定,它的分子和分母成正比例.
.(判断对错)
22.式子=k(一定)表示的是正比例关系.
.(判断对错)
23.比例尺l:100说明图上的1厘米表示实际的距离100米.
.(判断对错)
24.如果x与y成反比例,那么3x与y也成反比例.
.
25.如果3X=4Y(X,Y均不为0),那么X:Y=4:3,X和Y成正比例.
(判断对错)
四.应用题(共7小题)
26.淘淘家在装修房屋时,买了同样大小的地板砖,铺地面积与所需块数的关系如图.他家的客厅面积是36m2,需要铺多少块这样的地板砖?(用比例解决问题)
27.汽车数量与运货质量的数据如下表,根据表中的数据回答下面各题.
汽车数量/辆
1
2
3
4
5
6
7
运货质量/吨
4
8
12
16
20
24
28
(1)表中
和
是两种相关联的量,
随着
的变化而变化.
(2)写出几组这两种量中相对应的两个数的比,求出比值,并比较比值的大小.
(3)上面求出的比值表示的意义是什么?
(4)表中相关联的两种量成正比例吗?为什么?
28.图表示了矿泉水的数量与总价的关系,看图回答问题.
①5瓶的总价是
元.
②12瓶的总价是
元.
③
瓶的总价是36元.
29.组装一批电动车,每天组装的辆数和需要的天数如表.
每天组装辆数
20
15
10
需要的天数
12
15
(1)请把上表补充完整.
(2)每天组装的辆数和需要的天数成什么比例?为什么?
(3)如果每天组装30辆,需要组装多少天?如果打算4天完成组装任务,每天需要组装多少辆?
30.一艘轮船从甲港开到乙港,3时行驶了75km.从乙港开到丙港,5时行驶了125km.
(1)分别求轮船从甲港开到乙港,从乙港开到丙港的速度.
(2)轮船行驶的路程和所用时间成什么比例?
(3)用等式把题目里的数量关系表示出来.
31.农业基地里的樱桃树比苹果树少350棵,樱桃树与苹果树的棵数比是3:5,基地里的樱桃树和苹果树各有多少棵?
32.六年级三个班的学生共植树420棵。甲班植的棵数是总数的40%,乙、丙两班植的棵数的比为11:10。三个班各植树多少棵?
参考答案与试题解析
一.选择题(共10小题)
1.解:A.x+y=10,x与y的和一定,不符合正比例的意义;
B.y﹣x=10,x与y的差一定,不符合正比例的意义;
C.由y=10x得=,所以x、y比值一定,x与y成正比例,符合题意;
故选:C.
2.解:正方形的周长÷边长=4(一定),是比值一定,所以正方形的周长和它的边长成正比例;
故选:A.
3.解:A选项:速度×时间=路程(一定),速度和时间乘积一定,成反比例;
B选项:被减数﹣差=被减数(一定),被减数和差是和与差的关系,乘积和比值都不是一定的,不成任何比例;
C选项:平行四边形的底×高=面积(一定),平行四边形的底和高的乘积一定,成反比例关系.
故选:B。
4.解:A×=B×,
因为<,
所以A>B.
故选:A.
5.解:A、xy=3,x和y成反比例;
B、x÷y=,x和y成正比例;
C、y﹣x=﹣3,x和y不成比例;
D、2x=40+y,2x﹣y=40,x和y不成比例.
故选:B.
6.解:y:x=20:8=2.5;
所以,y=40×2.5=100.
x
8
40
y
20
100
故选:B.
7.解:A、因为底×高=面积×2(一定),乘积一定,所以三角形的面积一定,它的底和高成反比例;
B、因为路程÷时间=速度(一定),比值一定,所以行驶的时间和路程成正比例;
C、商场营业时间一定,每天接待顾客的数量和营业额不成比例;
D、已修长度+未修长度=总长度(一定),和一定,所以已修的长度和未修的长度不成比例.
故选:A.
8.解:(70×)×(70×)
=(70×)×(70×)
=28×21
=588(平方米)
答:这块长方形果园的面积是588m2.
故选:C.
9.解:从题中可以得到以下数量关系:
单价×数量=总价(一定),
可以看出,单价和数量是两种相关联的量,单价随数量的变化而变化.总价一定,也就是单价与数量相对应数的乘积一定,符合反比例的意义.所以单价与数量成反比例关系.
故选:B。
10.解:因为=y
所以xy=k+5(一定)
(k一定,所以k+5也是一定的)
x和y的积是定值,
所以x和y成反比例关系,
故选:B。
二.填空题(共10小题)
11.解:240÷60=4(小时);
240×2÷(240÷40+4);
=480÷(6+4);
=480÷10;
=48(千米);
答:王飞往返的平均速度是每小时行48千米.
12.解:(1)C÷A=B(一定),是比值一定,A和C成正比例;
(2)A×B=C(一定),是乘积一定,A和B成反比例.
故答案为:正比例,反比例.
13.解:因为,S=ah×,面积一定,所以底与高成反比例关系.
故答案为:反.
14.解:因为=c,所以b×c=a(一定),是乘积一定,b和c就成反比例;
因为=c,所以a÷c=b(一定),是比值一定,a和c就成正比例.
故答案为:反,正.
15.解:以“单价、数量、总量”之间的数量关系为例分析解答.
①总价:数量=单价(一定),
可以看出,总价和数量是两种相关联的量,总价随数量的变化而变化.单价一定,也就是总价与数量相对应数的比值一定.所以总价与数量成正比例.
②单价×数量=总价(一定),
可以看出,单价和数量是两种相关联的量,单价随数量的变化而变化.总价一定,也就是单价与数量相对应数的乘积一定.所以单价与数量成反比例关系.
故答案为:单价,总价,数量,总价,单价,数量(也可以是其它数量关系中的量).
16.解:x和y都不为0.如果y=x,则:
y÷x=(一定),比值一定,符合正比例的含义,所以x和y成正比例;
如果=,
符合正比例的意义,则xy=3×5=15(一定),乘积一定,所以x和y成
反比例.
故答案为:正,反.
17.解:因为ab=c,即c:a=b(一定),比值一定,所以a和c成正比例;
因为ab=c(一定),乘积一定,所以a和b成反比例;
故答案为:正、反.
18.解:(1)统计表见下图:
时间/秒
20
40
出水量/升
4
8
(2)因为20:4=40:8=5(一定),
是这个水龙头的出水量和打开的时间的比值一定,
符合正比例的意义,所以这个水龙头打开的时间和出水量成成正比例.
每秒的出水量:2÷10=0.2(升),
9.6÷0.2=48(秒).
(3)0.2×20=4(升),0.2×50=10(升)
10﹣4=6(升),6÷10×100%=60%
故答案为:4,8,正,48,60.
19.解:甲:乙=2:3
3×甲=2×乙,
甲=乙;
因为:乙是丙的,
所以:乙:丙=4:5,
丙=乙;
甲:乙:丙=乙:乙:乙
甲:乙:丙=8:12:15;
8+12+15=35(份),
70×3×
=210×,
=72.
答:乙数是72.
20.解:如果A和B成正比例,那么=,根据比例的基本性质,求出x=2;
如果A和B成反比例,那么2×0.5=8x,求出x=0.125.
故答案为:2,0.125.
三.判断题(共5小题)
21.解:=分数值(一定),是比值一定,分子和分母成正比例.
故判断为:正确.
22.解:因为=k(一定),所以这是表示x、y成正比例的式子.
故答案为:√.
23.解:比例尺l:100说明图上的1厘米表示实际的距离100厘米.
故答案为:×
24.解:x
与y成反比例,说明x×y=k,k一定,
3x×y=3k,3是一个常数,所以,3k一定,故3x和y也成比例;
故答案为:√.
25.解:因为3X=4Y(X,Y均不为0),
所以X:Y=4:3=(一定),
符合正比例的意义,所以X与Y成正比例。
故答案为:√。
四.应用题(共7小题)
26.解:根据题意与分析可得:铺地面积与所需块数成正比例关系;
设需要铺x块这样的地板砖,根据题意,可得:
36:x=2:8
2x=36×8
2x÷2=36×8÷2
x=144
答:需要铺144块这样的地板砖.
27.解:(1)表中有汽车数量和运货质量两种量,它们是两种相关联的量,一个量变大,另一个量也随着变大,它们的比值一定,所以汽车数量和运货质量成正比例关系.
(2)4:1=4,8:2=4,12:3=4,16:4=4,它们的比值相等.
(3)根据题意可知,这个比值表示每辆汽车的运货质量.
(4)相关联的两种量成正比例,因为它们的比值一定.
故答案为:汽车数量;运货质量;运货质量;汽车数量.
28.解:(1)5瓶的售价是10元.
(2)10÷5×12
=2×12
=24(元);
答:12瓶的售价是
24元.
(3)36÷(10÷5)
=36÷2
=18(瓶);
答:18瓶的售价是36元.
故答案为:10,24,18.
29.解:(1)15×12=180(辆)
180÷20=9(天)
180÷15=12(辆)
180÷10=18(天)
每天组装辆数
20
15
12
10
需要的天数
9
12
15
18
(2)因为每天组装辆数×需要的天数=180辆(一定),即乘积一定.所以每天组装的辆数和需要的天数成反比例.
(3)180÷30=6(天)
180÷4=45(辆)
答:每天组装30辆,需要组装6天;打算4天完成组装任务,每天需要组装45辆.
故答案为:12,9,18.
30.解:从甲港开到乙港的速度:75÷3=25(千米/时).
从乙港开到丙港的速度:125÷5=25(千米/时).
答:轮船从甲港开到乙港,从乙港开到丙港的速度都是25千米/时.
(2)由(1)可知=25(一定),是比值一定,所以轮船行驶的路程和所用时间成正比例.
(3)设s表示路程,t表示时间,v表示速度,则等量关系为:=v.
31.解:350÷(5﹣3)
=350÷2
=175(棵)
175×3=525(棵)
175×5=875(棵)
答:基地里的樱桃树525棵,苹果树875棵。
32.解:420×40%=168(棵)
(420﹣168)÷(11+10)
=252÷21
=12(棵)
12×11=132(棵)
12×10=120(棵)
答:甲班植树168棵,乙班植树132棵,丙班植树120棵。
