《椭圆的定义及标准方程》公开课课件(共30张PPT)
文档属性
| 名称 | 《椭圆的定义及标准方程》公开课课件(共30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 23.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-13 22:19:48 | ||
图片预览








文档简介
(共30张PPT)
情景导入
情景导入
情景导入
情景导入
情景导入
情景导入
情景导入
情景导入
椭圆
定义及其标准方程
展示课题
展示课题
1、椭圆的定义及焦点、焦距
2、椭圆的标准方程及其特点
3、求简单的椭圆的标准方程
4、了解建立曲线方程的基本方法,体会数形结合
5、培养观察能力、归纳能力、探索能力
目标:
展示目标
展示目标
难点:
1、椭圆标准方程的推导
2、辨析椭圆的标准方程
重点:
1、感受建立曲线方程的基本过程
2、椭圆标准方程的推导,求简单的椭圆方程
?自然界处处存在着椭圆,我们如何用自己的双手画出椭圆呢?
?先回忆一下,我们是如何画圆的呢?
圆的定义:
平面上到定点的距离等于定长的点的集合叫圆.
新知导学
新知导学
【温故而知新】
【想一想】
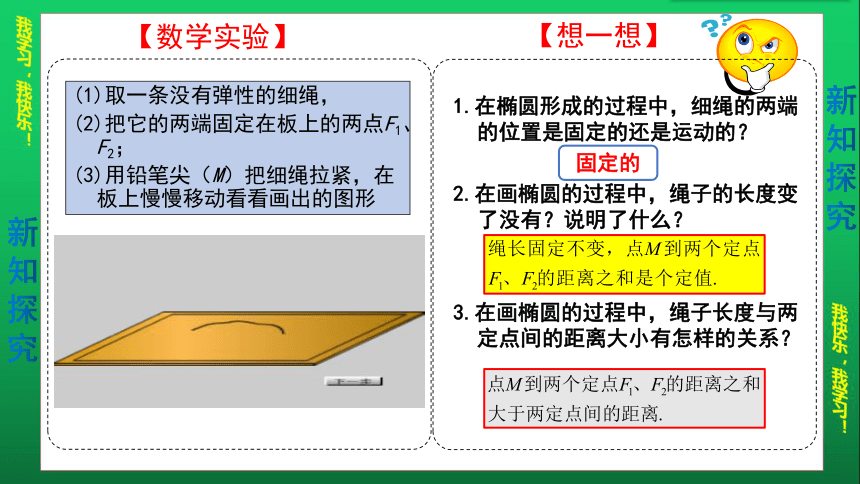
(1)取一条没有弹性的细绳,
(2)把它的两端固定在板上的两点F1、F2;
(3)用铅笔尖(M)把细绳拉紧,在板上慢慢移动看看画出的图形
1.在椭圆形成的过程中,细绳的两端的位置是固定的还是运动的?
2.在画椭圆的过程中,绳子的长度变了没有?说明了什么?
3.在画椭圆的过程中,绳子长度与两定点间的距离大小有怎样的关系?
固定的
新知探究
新知探究
【数学实验】
【想一想】
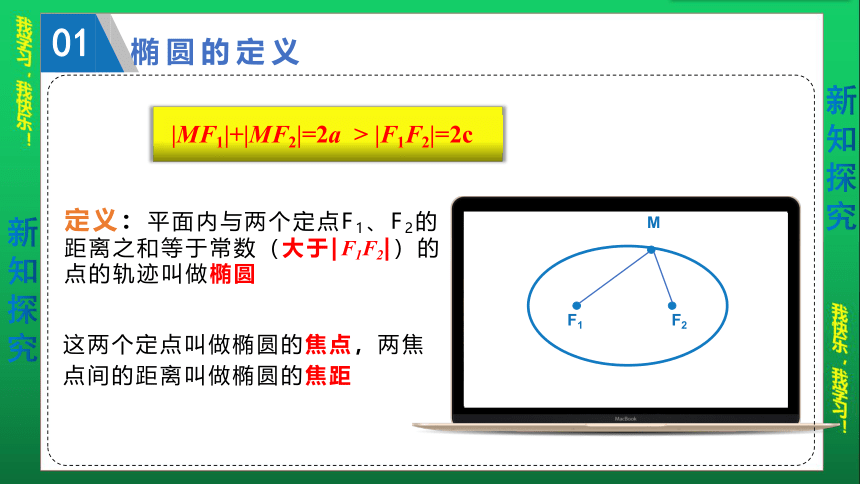
|MF1|+|MF2|=2a
>
|F1F2|=2c
定义:平面内与两个定点F1、F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆
这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距
M
F2
F1
椭圆的定义
01
新知探究
新知探究
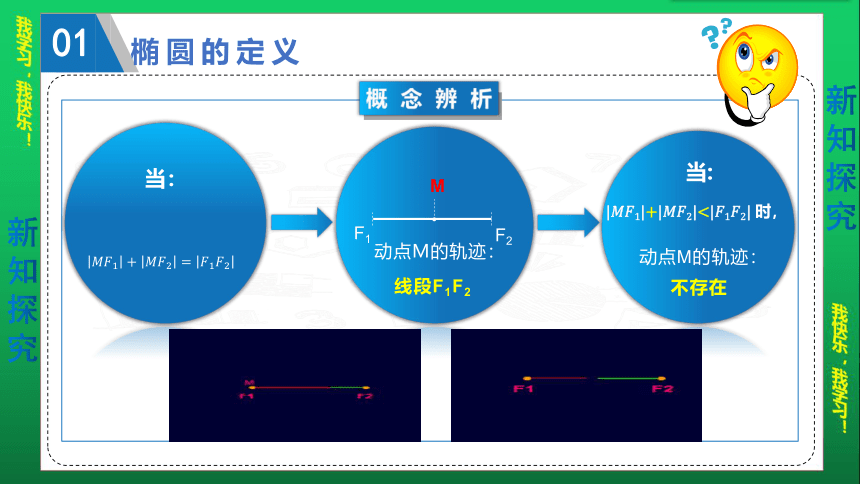
概念辨析
当:
F1
F2
M
动点M的轨迹:
线段F1F2
当:
|??1|+|??2|<|?1?2|
时,
动点M的轨迹:
不存在
新知探究
新知探究
椭圆的定义
01
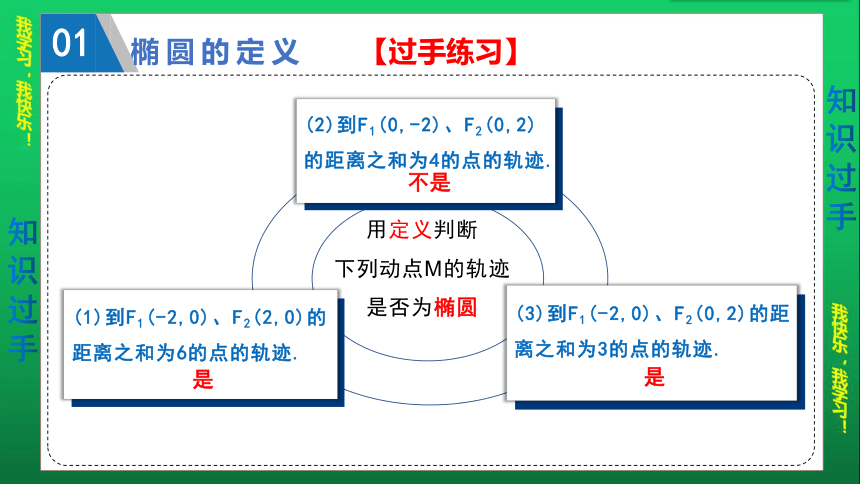
用定义判断
下列动点M的轨迹
是否为椭圆
(1)到F1(-2,0)、F2(2,0)的距离之和为6的点的轨迹.
(2)到F1(0,-2)、F2(0,2)的距离之和为4的点的轨迹.
不是
是
(3)到F1(-2,0)、F2(0,2)的距离之和为3的点的轨迹.
是
【过手练习】
知识过手
知识过手
椭圆的定义
01
椭圆标准方程的推导
02
M
F2
F1
O
y
x
基本步骤:
建
建系
1
设
设动点坐标
2
列
列等式
3
代
代坐标
4
化
化简方程、证明
5
新知探究
新知探究
定义法求轨迹方程。
x
O
y
建系
1
设标
2
列式
3
化简
4
M(x,y)
F2
F1
以F1、F2
所在直线为
x
轴,线段
F1F2的垂直平分线为
y
轴,建立直角坐标系.
设
M(
x,y
)是椭圆上任意一点
|F1F2|=2c(c>0),则有F1(-c,0)、F2(c,0)
又设M与F1、F2的距离之和等于2a.
椭圆上的点M(x,y)属于集合
P={M︱|MF1|+
|
MF2
|=2a}
x
O
y
M(x,y)
F2
F1
则:
02
新知探究
新知探究
椭圆标准方程的推导
p
F2
F1
O
x
y
>0
你能从图中找出表示a
,c,
的线
段吗?
由椭圆的定义可知,
2a>2c,即a>c;
02
新知探究
新知探究
椭圆标准方程的推导
a
c
b
?OPF2中,能用a、c表示|OP|吗?
p
F2
F1
O
x
y
02
新知探究
新知探究
椭圆标准方程的推导
焦点在x轴的椭圆的标准方程为:
焦点在y
轴上的椭圆的标准方程呢?
焦点在x轴的椭圆的标准方程为:
F2
F1
O
y
x
将X轴与Y轴交换一下,焦点不就在Y轴上了吗?你能直接写出此椭圆的方程吗?
椭圆标准方程的特点
03
新知探究
新知探究
x2与y2的分母哪个大,焦点就在对应的那个轴上
平面内到两个定点F1,F2的距离的和等
于常数(大于|F1F2|)的点的轨迹
标准方程
不
同
点
相
同
点
图
形
焦点坐标
定
义
a、b、c
的关系
焦点位置的判断
x
y
F1
F2
P
O
x
y
F1
F2
P
O
,a最大
则a=
,b=
;
,则a=
,b=
;
5
3
3
2
焦点坐标为:___________
焦距等于___;
(-4,0)(4,0)
8
焦点坐标为:_____
______
焦距等于______
【过手练习】
知识过手
知识过手
c=
,
4
c=
,
3.已知方程
表示焦点在x轴
上的椭圆,则m的取值范围是
.
椭圆标准方程的特点
03
焦点在___轴上
x
焦点在___轴上
y
典例分析
典例分析
例1:
写出适合下列条件的椭圆标准方程:
a=2,c=1,焦点在x轴上;
解:
由题意可知:
c=1
a=2、
因此,这个椭圆的标准方程是:
因为焦点在x轴上,所以设它的标准方程为:
根据焦点位置设出恰当的方程
2、再定量(a,b,c)
1
、先定位(焦点)
3、代入
标准方程即可求得
小结:
04
求椭圆的标准方程
待定系数法求轨迹方程
焦点在x轴上,x2与y2
的分母谁大些
焦点在x轴上,x2
的分母大些
知识过手
知识过手
写出适合下列条件的椭圆标准方程:
解:
由题意可知:
b=1、
因此,这个椭圆的标准方程是:
因为焦点在y轴上,所以设它的标准方程为:
b=1,
焦点在y轴上
【过手练习】
04
求椭圆的标准方程
典例分析
典例分析
例2:求适合下列条件的椭圆的标准方程:
两个焦点的坐标分别是F1(-2,0),F2(2,0),并且椭圆经过点P(2,3)
解:
由椭圆的定义可知:
所以椭圆的标准方程为:
因为椭圆的焦点在X轴上,所以设它的标准方程为
-2
2
P(2,3)
y
x
o
04
求椭圆的标准方程
知识过手
知识过手
求适合下列条件的椭圆的标准方程:
两焦点的坐标分别是(0,-4),(0,4),椭圆上的一定点P到
两焦点距离的和等于10。
解:
由题意可知:
2c=8、
2a=10、
∴a=5,c=4
∴这个椭圆的标准方程是:
因为焦点在y轴上,所以设它的标准方程为:
-4
4
y
x
o
04
求椭圆的标准方程
【变式训练】
拓展思维
拓展思维
已知a=5,c=4,求椭圆的标准方程。
解:
∵a=5,c=4
∴当焦点在x轴上,这个椭圆的标准方程是:
04
求椭圆的标准方程
例3:
∴当焦点在y轴上,这个椭圆的标准方程是:
拓展思维
拓展思维
已知b=5,c=4,求椭圆的标准方程。
解:
∵b=5,c=4
∴当焦点在x轴上,这个椭圆的标准方程是:
04
求椭圆的标准方程
∴当焦点在y轴上,这个椭圆的标准方程是:
【变式训练】
总结提升
总结提升
1.学习了椭圆的定义,焦点、焦距,
2.椭圆的标准方程
05
课堂总结
a2-b2=c2,
a>b>0
|MF1|+|MF2|=2a
>
|F1F2|=2c
|F1F2|=2c
你都学到了什么?
3.a、b、c的关系,始终满足
椭圆标准方程有什么特点?
x2与y2的分母哪个大,焦点就在对应的那个轴上
分层作业
分层作业
【必做】
【选做】
1.椭圆
的焦距是(
)
A
1
B
2
C
4
D
2.已知焦点F1(-6,0),F2(6,0),2a=20的椭圆标准方程为:
3.椭圆
上的一点P到焦点F1的
距离等于6,那么点P到另外的一个焦点F2的距离是_____
4.已知方程
表示焦点在y轴
上的椭圆,则m的取值范围是
.
1.用定义推导焦点在y轴上的椭圆的标准方程。
2.已知方程
表示
焦点在x轴上的椭圆,则m的取值范围
是
.
作业
安全教育
安全教育
安全提醒
1、课间不要在教室及过道追逐打闹,预防磕碰摔倒
2、上下楼梯不要推拉,预防踩踏
3、天气冷了,注意添加衣服,预防感冒
4、其他安全注意事项
椭圆及其标准方程
下课
1.已知F1,F2
是椭圆
的两个焦点。A、B为过点F1的直线与椭圆的两个交点。则△AF1F2
的周长为__
__
拓展练习
拓展练习
2:已知方程
表示焦点在X轴上的椭圆,
则m的取值范围是
.
高考链接
3.椭圆 上一点P到一个焦点的距离为5,则
P
到另一个焦点的距离为(
)
A.5
B.6
C.4
D.10
4.已知椭圆的方程为
,焦点在X轴上,则其焦距为(
)
A、2
B、2
C、2
D、
拓展练习
拓展练习
高考链接
情景导入
情景导入
情景导入
情景导入
情景导入
情景导入
情景导入
情景导入
椭圆
定义及其标准方程
展示课题
展示课题
1、椭圆的定义及焦点、焦距
2、椭圆的标准方程及其特点
3、求简单的椭圆的标准方程
4、了解建立曲线方程的基本方法,体会数形结合
5、培养观察能力、归纳能力、探索能力
目标:
展示目标
展示目标
难点:
1、椭圆标准方程的推导
2、辨析椭圆的标准方程
重点:
1、感受建立曲线方程的基本过程
2、椭圆标准方程的推导,求简单的椭圆方程
?自然界处处存在着椭圆,我们如何用自己的双手画出椭圆呢?
?先回忆一下,我们是如何画圆的呢?
圆的定义:
平面上到定点的距离等于定长的点的集合叫圆.
新知导学
新知导学
【温故而知新】
【想一想】
(1)取一条没有弹性的细绳,
(2)把它的两端固定在板上的两点F1、F2;
(3)用铅笔尖(M)把细绳拉紧,在板上慢慢移动看看画出的图形
1.在椭圆形成的过程中,细绳的两端的位置是固定的还是运动的?
2.在画椭圆的过程中,绳子的长度变了没有?说明了什么?
3.在画椭圆的过程中,绳子长度与两定点间的距离大小有怎样的关系?
固定的
新知探究
新知探究
【数学实验】
【想一想】
|MF1|+|MF2|=2a
>
|F1F2|=2c
定义:平面内与两个定点F1、F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆
这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距
M
F2
F1
椭圆的定义
01
新知探究
新知探究
概念辨析
当:
F1
F2
M
动点M的轨迹:
线段F1F2
当:
|??1|+|??2|<|?1?2|
时,
动点M的轨迹:
不存在
新知探究
新知探究
椭圆的定义
01
用定义判断
下列动点M的轨迹
是否为椭圆
(1)到F1(-2,0)、F2(2,0)的距离之和为6的点的轨迹.
(2)到F1(0,-2)、F2(0,2)的距离之和为4的点的轨迹.
不是
是
(3)到F1(-2,0)、F2(0,2)的距离之和为3的点的轨迹.
是
【过手练习】
知识过手
知识过手
椭圆的定义
01
椭圆标准方程的推导
02
M
F2
F1
O
y
x
基本步骤:
建
建系
1
设
设动点坐标
2
列
列等式
3
代
代坐标
4
化
化简方程、证明
5
新知探究
新知探究
定义法求轨迹方程。
x
O
y
建系
1
设标
2
列式
3
化简
4
M(x,y)
F2
F1
以F1、F2
所在直线为
x
轴,线段
F1F2的垂直平分线为
y
轴,建立直角坐标系.
设
M(
x,y
)是椭圆上任意一点
|F1F2|=2c(c>0),则有F1(-c,0)、F2(c,0)
又设M与F1、F2的距离之和等于2a.
椭圆上的点M(x,y)属于集合
P={M︱|MF1|+
|
MF2
|=2a}
x
O
y
M(x,y)
F2
F1
则:
02
新知探究
新知探究
椭圆标准方程的推导
p
F2
F1
O
x
y
>0
你能从图中找出表示a
,c,
的线
段吗?
由椭圆的定义可知,
2a>2c,即a>c;
02
新知探究
新知探究
椭圆标准方程的推导
a
c
b
?OPF2中,能用a、c表示|OP|吗?
p
F2
F1
O
x
y
02
新知探究
新知探究
椭圆标准方程的推导
焦点在x轴的椭圆的标准方程为:
焦点在y
轴上的椭圆的标准方程呢?
焦点在x轴的椭圆的标准方程为:
F2
F1
O
y
x
将X轴与Y轴交换一下,焦点不就在Y轴上了吗?你能直接写出此椭圆的方程吗?
椭圆标准方程的特点
03
新知探究
新知探究
x2与y2的分母哪个大,焦点就在对应的那个轴上
平面内到两个定点F1,F2的距离的和等
于常数(大于|F1F2|)的点的轨迹
标准方程
不
同
点
相
同
点
图
形
焦点坐标
定
义
a、b、c
的关系
焦点位置的判断
x
y
F1
F2
P
O
x
y
F1
F2
P
O
,a最大
则a=
,b=
;
,则a=
,b=
;
5
3
3
2
焦点坐标为:___________
焦距等于___;
(-4,0)(4,0)
8
焦点坐标为:_____
______
焦距等于______
【过手练习】
知识过手
知识过手
c=
,
4
c=
,
3.已知方程
表示焦点在x轴
上的椭圆,则m的取值范围是
.
椭圆标准方程的特点
03
焦点在___轴上
x
焦点在___轴上
y
典例分析
典例分析
例1:
写出适合下列条件的椭圆标准方程:
a=2,c=1,焦点在x轴上;
解:
由题意可知:
c=1
a=2、
因此,这个椭圆的标准方程是:
因为焦点在x轴上,所以设它的标准方程为:
根据焦点位置设出恰当的方程
2、再定量(a,b,c)
1
、先定位(焦点)
3、代入
标准方程即可求得
小结:
04
求椭圆的标准方程
待定系数法求轨迹方程
焦点在x轴上,x2与y2
的分母谁大些
焦点在x轴上,x2
的分母大些
知识过手
知识过手
写出适合下列条件的椭圆标准方程:
解:
由题意可知:
b=1、
因此,这个椭圆的标准方程是:
因为焦点在y轴上,所以设它的标准方程为:
b=1,
焦点在y轴上
【过手练习】
04
求椭圆的标准方程
典例分析
典例分析
例2:求适合下列条件的椭圆的标准方程:
两个焦点的坐标分别是F1(-2,0),F2(2,0),并且椭圆经过点P(2,3)
解:
由椭圆的定义可知:
所以椭圆的标准方程为:
因为椭圆的焦点在X轴上,所以设它的标准方程为
-2
2
P(2,3)
y
x
o
04
求椭圆的标准方程
知识过手
知识过手
求适合下列条件的椭圆的标准方程:
两焦点的坐标分别是(0,-4),(0,4),椭圆上的一定点P到
两焦点距离的和等于10。
解:
由题意可知:
2c=8、
2a=10、
∴a=5,c=4
∴这个椭圆的标准方程是:
因为焦点在y轴上,所以设它的标准方程为:
-4
4
y
x
o
04
求椭圆的标准方程
【变式训练】
拓展思维
拓展思维
已知a=5,c=4,求椭圆的标准方程。
解:
∵a=5,c=4
∴当焦点在x轴上,这个椭圆的标准方程是:
04
求椭圆的标准方程
例3:
∴当焦点在y轴上,这个椭圆的标准方程是:
拓展思维
拓展思维
已知b=5,c=4,求椭圆的标准方程。
解:
∵b=5,c=4
∴当焦点在x轴上,这个椭圆的标准方程是:
04
求椭圆的标准方程
∴当焦点在y轴上,这个椭圆的标准方程是:
【变式训练】
总结提升
总结提升
1.学习了椭圆的定义,焦点、焦距,
2.椭圆的标准方程
05
课堂总结
a2-b2=c2,
a>b>0
|MF1|+|MF2|=2a
>
|F1F2|=2c
|F1F2|=2c
你都学到了什么?
3.a、b、c的关系,始终满足
椭圆标准方程有什么特点?
x2与y2的分母哪个大,焦点就在对应的那个轴上
分层作业
分层作业
【必做】
【选做】
1.椭圆
的焦距是(
)
A
1
B
2
C
4
D
2.已知焦点F1(-6,0),F2(6,0),2a=20的椭圆标准方程为:
3.椭圆
上的一点P到焦点F1的
距离等于6,那么点P到另外的一个焦点F2的距离是_____
4.已知方程
表示焦点在y轴
上的椭圆,则m的取值范围是
.
1.用定义推导焦点在y轴上的椭圆的标准方程。
2.已知方程
表示
焦点在x轴上的椭圆,则m的取值范围
是
.
作业
安全教育
安全教育
安全提醒
1、课间不要在教室及过道追逐打闹,预防磕碰摔倒
2、上下楼梯不要推拉,预防踩踏
3、天气冷了,注意添加衣服,预防感冒
4、其他安全注意事项
椭圆及其标准方程
下课
1.已知F1,F2
是椭圆
的两个焦点。A、B为过点F1的直线与椭圆的两个交点。则△AF1F2
的周长为__
__
拓展练习
拓展练习
2:已知方程
表示焦点在X轴上的椭圆,
则m的取值范围是
.
高考链接
3.椭圆 上一点P到一个焦点的距离为5,则
P
到另一个焦点的距离为(
)
A.5
B.6
C.4
D.10
4.已知椭圆的方程为
,焦点在X轴上,则其焦距为(
)
A、2
B、2
C、2
D、
拓展练习
拓展练习
高考链接
