圆周角
图片预览
文档简介
圆周角
义龙中学 陈航
一、复习圆心角
师:上节课我们学习了圆中的什么角,特点是什么?
生:圆心角,顶点在圆心。
二、圆周角的定义
1、定义
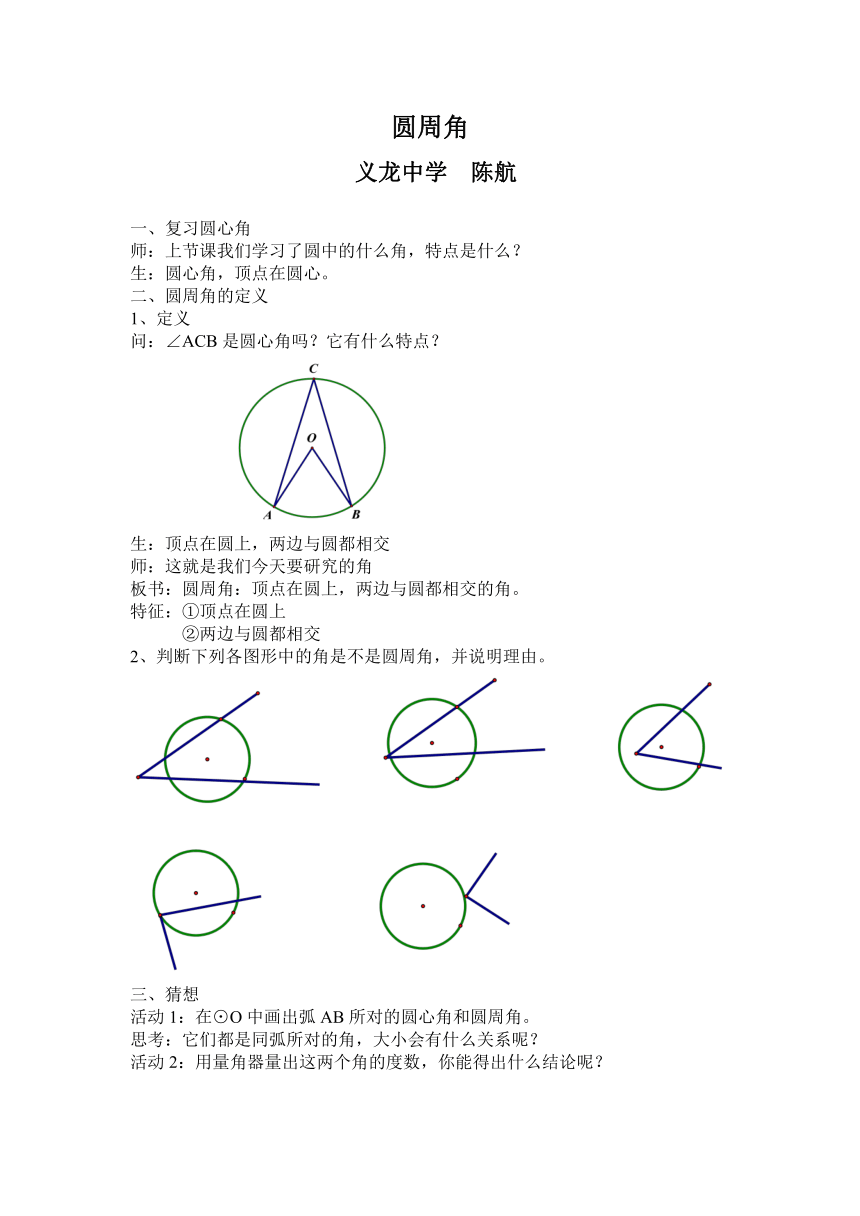
问:∠ACB是圆心角吗?它有什么特点?
生:顶点在圆上,两边与圆都相交
师:这就是我们今天要研究的角
板书:圆周角:顶点在圆上,两边与圆都相交的角。
特征:①顶点在圆上
②两边与圆都相交
2、判断下列各图形中的角是不是圆周角,并说明理由。
三、猜想
活动1:在⊙O中画出弧AB所对的圆心角和圆周角。
思考:它们都是同弧所对的角,大小会有什么关系呢?
活动2:用量角器量出这两个角的度数,你能得出什么结论呢?
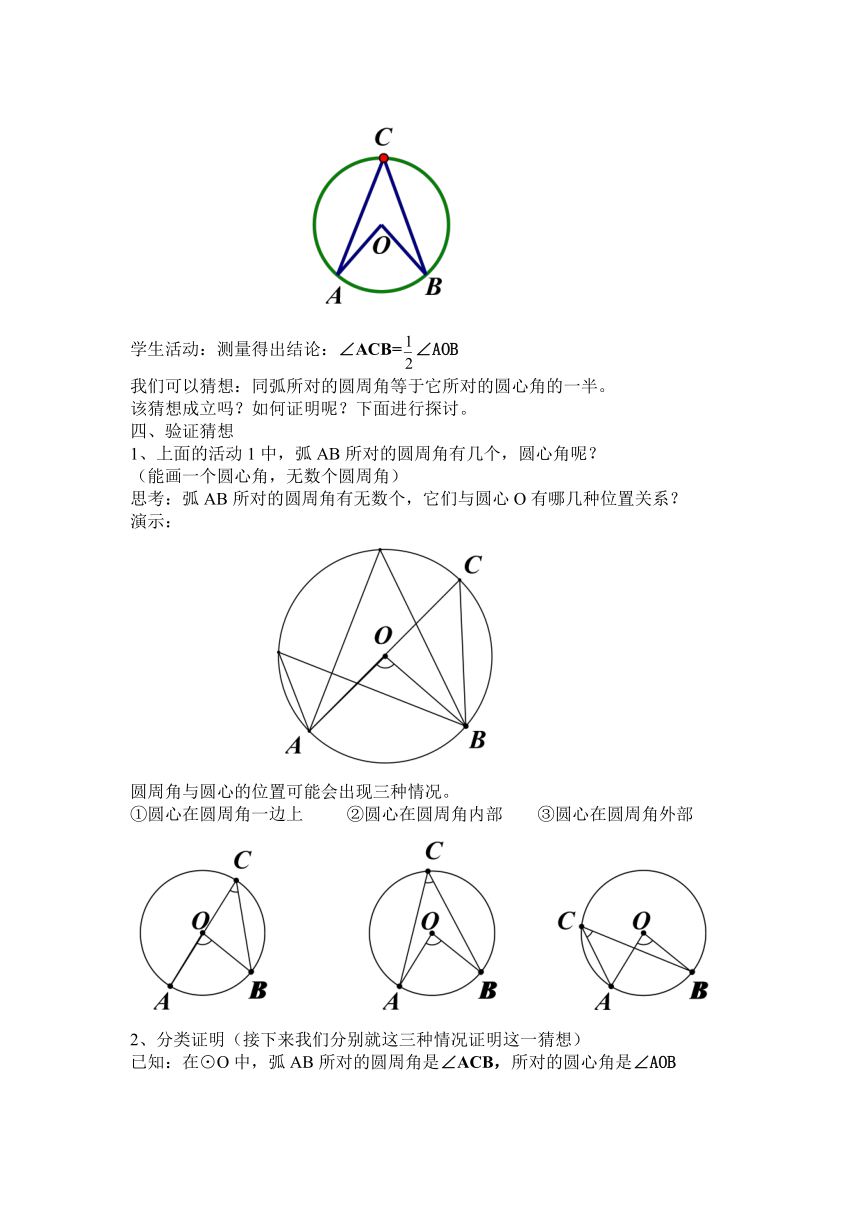
学生活动:测量得出结论:∠ACB=∠AOB
我们可以猜想:同弧所对的圆周角等于它所对的圆心角的一半。
该猜想成立吗?如何证明呢?下面进行探讨。
四、验证猜想
1、上面的活动1中,弧AB所对的圆周角有几个,圆心角呢?
(能画一个圆心角,无数个圆周角)
思考:弧AB所对的圆周角有无数个,它们与圆心O有哪几种位置关系?
演示:
圆周角与圆心的位置可能会出现三种情况。
①圆心在圆周角一边上 ②圆心在圆周角内部 ③圆心在圆周角外部
2、分类证明(接下来我们分别就这三种情况证明这一猜想)
已知:在⊙O中,弧AB所对的圆周角是∠ACB,所对的圆心角是∠AOB
求证:∠ACB=∠AOB
证明:(1)圆心在边AC上
∵OB=OC
∴∠B=∠C
∵∠AOB是△BOC的外角
∴ ∠AOB=∠B+∠C=2∠C
∴ ∠ACB=∠AOB
(2)(3)由学生分组讨论,展示结果
(2)圆心在∠ACB内部
作直径CD
∠ACD=∠AOD ,∠BCD=∠BOD
∴∠ACB=∠ACD+∠BCD=(∠AOD+∠BOD)
∴∠ACB=∠AOB
利用(1)结论得
即∠ACB=∠AOB
(3)圆心在∠ACB外部
作直径CD
由(1)知
∠BCD=∠BOD , ∠ACD=∠AOD
∴∠ACB=∠ACD-∠BCD=∠AOD-∠BOD
∴∠ACB=(∠BOD-∠AOD)
∴∠ACB=∠AOB
综上所诉,在一个圆中,同弧所对的圆周角是它所对的圆心角的一半。这就是圆周角定理。
板书:在同圆或等圆中,同弧或等弧所对的圆周角等于它所对圆心角的一半。
3、思考:同一条弧可以作出无数个圆周角,它们的大小有什么关系呢?
结论:都相等
逆向定理也成立,即相等的圆周角所对的弧相等
板书(结合以上):圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于它所对圆心角的一半;相等的圆周角所对的弧相等。
五、应用
1、求图中∠α的度数
∠α= ∠α=
2、如图,点A、B、C、D都在⊙O上,∠DAC=∠BAC=60°,则△BCD是 三角形。
3、如图,∠B=50°,点A′从点C沿弧AC运动到点A,则∠A′OC变化的范围是
4、 1.如图AB是⊙O直径,你能否求出∠ACB=?
结论:直径或半圆所对的圆周角都等于90°
5、 如图,若圆周角∠ACB=90°,那么弦AB是直径吗?
逆向结论:90°的圆周角所对的弦是直径.
板书:直径或半圆所对的圆周角都等于90°
90°的圆周角所对的弦是直径.
6、请你帮助用直角曲尺检查半圆形的工件,哪个是合格的?为什么?
六、这节课你学到了哪些知识点?
1、圆周角定义
2、圆周角定理:
1、圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于它所对圆心角的一半;相等的圆周角所对的弧相等。
2、直径或半圆所对的圆周角都等于90°
3、90°的圆周角所对的弦是直径.
40°
O
A
B
C
α
70°
C
B
O
A
α
O
C
A′
A
B
O
C
B
A
A
B
O
C
义龙中学 陈航
一、复习圆心角
师:上节课我们学习了圆中的什么角,特点是什么?
生:圆心角,顶点在圆心。
二、圆周角的定义
1、定义
问:∠ACB是圆心角吗?它有什么特点?
生:顶点在圆上,两边与圆都相交
师:这就是我们今天要研究的角
板书:圆周角:顶点在圆上,两边与圆都相交的角。
特征:①顶点在圆上
②两边与圆都相交
2、判断下列各图形中的角是不是圆周角,并说明理由。
三、猜想
活动1:在⊙O中画出弧AB所对的圆心角和圆周角。
思考:它们都是同弧所对的角,大小会有什么关系呢?
活动2:用量角器量出这两个角的度数,你能得出什么结论呢?
学生活动:测量得出结论:∠ACB=∠AOB
我们可以猜想:同弧所对的圆周角等于它所对的圆心角的一半。
该猜想成立吗?如何证明呢?下面进行探讨。
四、验证猜想
1、上面的活动1中,弧AB所对的圆周角有几个,圆心角呢?
(能画一个圆心角,无数个圆周角)
思考:弧AB所对的圆周角有无数个,它们与圆心O有哪几种位置关系?
演示:
圆周角与圆心的位置可能会出现三种情况。
①圆心在圆周角一边上 ②圆心在圆周角内部 ③圆心在圆周角外部
2、分类证明(接下来我们分别就这三种情况证明这一猜想)
已知:在⊙O中,弧AB所对的圆周角是∠ACB,所对的圆心角是∠AOB
求证:∠ACB=∠AOB
证明:(1)圆心在边AC上
∵OB=OC
∴∠B=∠C
∵∠AOB是△BOC的外角
∴ ∠AOB=∠B+∠C=2∠C
∴ ∠ACB=∠AOB
(2)(3)由学生分组讨论,展示结果
(2)圆心在∠ACB内部
作直径CD
∠ACD=∠AOD ,∠BCD=∠BOD
∴∠ACB=∠ACD+∠BCD=(∠AOD+∠BOD)
∴∠ACB=∠AOB
利用(1)结论得
即∠ACB=∠AOB
(3)圆心在∠ACB外部
作直径CD
由(1)知
∠BCD=∠BOD , ∠ACD=∠AOD
∴∠ACB=∠ACD-∠BCD=∠AOD-∠BOD
∴∠ACB=(∠BOD-∠AOD)
∴∠ACB=∠AOB
综上所诉,在一个圆中,同弧所对的圆周角是它所对的圆心角的一半。这就是圆周角定理。
板书:在同圆或等圆中,同弧或等弧所对的圆周角等于它所对圆心角的一半。
3、思考:同一条弧可以作出无数个圆周角,它们的大小有什么关系呢?
结论:都相等
逆向定理也成立,即相等的圆周角所对的弧相等
板书(结合以上):圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于它所对圆心角的一半;相等的圆周角所对的弧相等。
五、应用
1、求图中∠α的度数
∠α= ∠α=
2、如图,点A、B、C、D都在⊙O上,∠DAC=∠BAC=60°,则△BCD是 三角形。
3、如图,∠B=50°,点A′从点C沿弧AC运动到点A,则∠A′OC变化的范围是
4、 1.如图AB是⊙O直径,你能否求出∠ACB=?
结论:直径或半圆所对的圆周角都等于90°
5、 如图,若圆周角∠ACB=90°,那么弦AB是直径吗?
逆向结论:90°的圆周角所对的弦是直径.
板书:直径或半圆所对的圆周角都等于90°
90°的圆周角所对的弦是直径.
6、请你帮助用直角曲尺检查半圆形的工件,哪个是合格的?为什么?
六、这节课你学到了哪些知识点?
1、圆周角定义
2、圆周角定理:
1、圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于它所对圆心角的一半;相等的圆周角所对的弧相等。
2、直径或半圆所对的圆周角都等于90°
3、90°的圆周角所对的弦是直径.
40°
O
A
B
C
α
70°
C
B
O
A
α
O
C
A′
A
B
O
C
B
A
A
B
O
C
