人教版数学必修四1.1.2《弧度制》教学设计Word
文档属性
| 名称 | 人教版数学必修四1.1.2《弧度制》教学设计Word |

|
|
| 格式 | zip | ||
| 文件大小 | 96.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-14 12:27:16 | ||
图片预览

文档简介
知识像烛光,能照亮一个人,也能照亮无数的人。--培根
知识像烛光,能照亮一个人,也能照亮无数的人。--培根
知识像烛光,能照亮一个人,也能照亮无数的人。--培根
《弧度制》教学设计
教学内容:
《普通高中课程标准试验教科书·数学》必修四第一章:三角函数§1.1任意角和弧度制§1.1.2弧度制
课
题:弧度制
三维目标:
1.通过类比长度、重量的不同度量制,使学生体会一个量可以用不同的单位制来度量,从而引出弧度制。
2.理解弧度制的意义,以及任意角的弧度数与弧长半径的关系。
3.能进行角度制与弧度制的互化。
4.通过探究使学生认识到角度制与弧度都是度量角的制度,从而使学生体会到事物之间总是相互联系的。
5.通过总结引入弧度制的好处,使学生学会归纳整理并认识到任何新知识的学习,都会为解决实际问题带来方便,从而激发学生的学习兴趣。
6.通过探究任意角的弧度数与弧长半径的关系,培养学生的合作意识和创新能力。
教学重点:理解弧度制的意义,能进行角度制与弧度制的互化
教学难点:弧度制的概念及其与角度的换算
课时安排:一课时
教学过程
一、课前布置任务
完成导学案中的自主学习部分,并尝试解决其它部分内容。
二、类比引入
1.由姚明的身高引入同一对象有不同的单位表示。
(设计意图是问题来源于实际生活,可以激发学生的兴趣,使得新知识的学习自然亲切)
2.在初中几何里,我们学过角的度量,1度的角是怎样定义的呢?角还有没有新的度量方法?
(教师顺势引导点明我们这节课要学习的内容,从而引出概念,这样以旧引新,符合学生的认知规律)
三、新知探究
1.定义:把长度等于半径长的弧所对的圆心角叫做1弧度的角.用符号rad表示。
弧度制的定义:用弧度做单位来度量角的制度叫做弧度制
说明:
(1)弧度制是以“弧度”为单位来度量角的单位制,角度制是以“度”为单位来度量角的单位制;
(2)1弧度是弧长等于半径长的圆弧所对的圆心角的大小,而1度是圆周的
所对的圆心角的大小;1弧度≠1?;
(3)弧度制是十进制,它的表示是用一个实数表示,而角度制是六十进制;
(4)今后在用弧度制表示角的时候,弧度二字或rad可以略去不写。
(设计意图是剖析概念可以帮助学生很好的理解概念的内涵和外延)
探究1:一定大小的圆心角与半径大小是否有关?
将角度固定,改变半径大小,计算弧长。
(结论:一定大小的圆心角与半径大小无关,意在说明弧度制定义的合理性。)
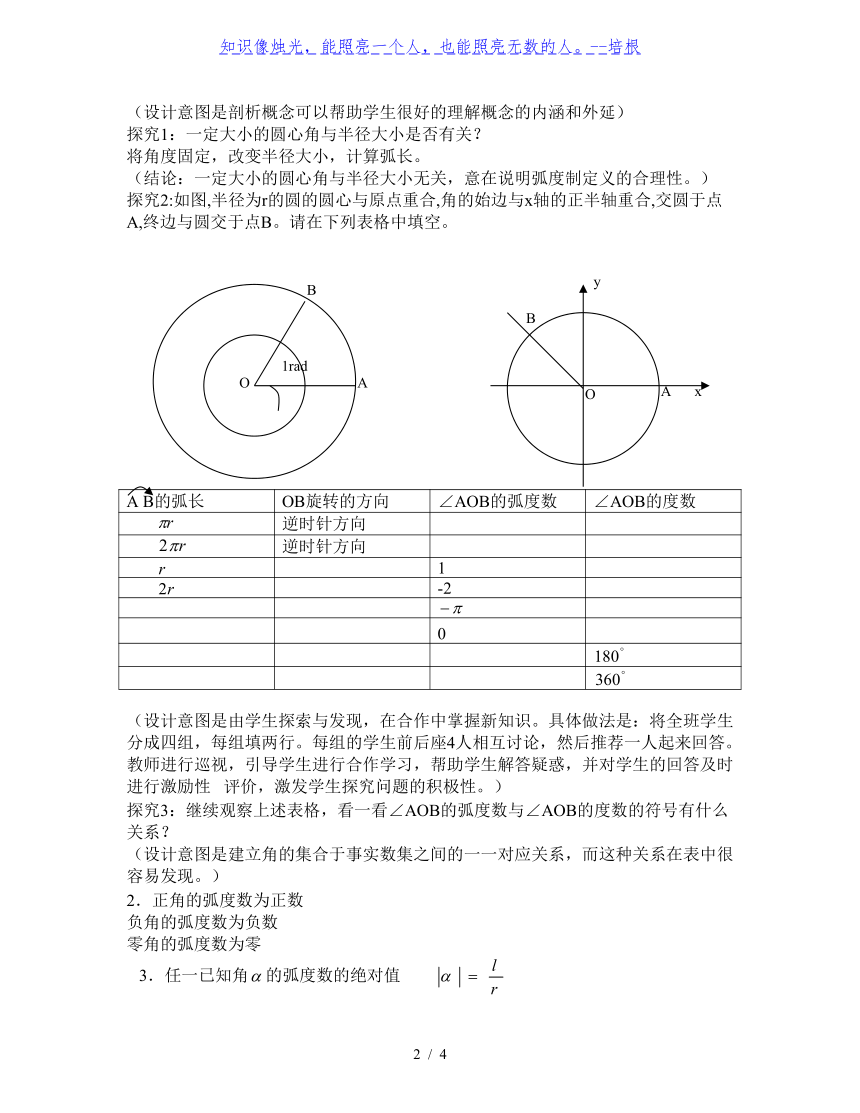
探究2:如图,半径为r的圆的圆心与原点重合,角的始边与x轴的正半轴重合,交圆于点A,终边与圆交于点B。请在下列表格中填空。
A
B的弧长
OB旋转的方向
∠AOB的弧度数
∠AOB的度数
逆时针方向
逆时针方向
1
-2
0
(设计意图是由学生探索与发现,在合作中掌握新知识。具体做法是:将全班学生分成四组,每组填两行。每组的学生前后座4人相互讨论,然后推荐一人起来回答。教师进行巡视,引导学生进行合作学习,帮助学生解答疑惑,并对学生的回答及时进行激励性评价,激发学生探究问题的积极性。)
探究3:继续观察上述表格,看一看∠AOB的弧度数与∠AOB的度数的符号有什么关系?
(设计意图是建立角的集合于事实数集之间的一一对应关系,而这种关系在表中很容易发现。)
2.正角的弧度数为正数
负角的弧度数为负数
零角的弧度数为零
3.任一已知角的弧度数的绝对值
其中
为以角
作为圆心角时所对圆弧的长,r为圆的半径.
5.角度制与弧度制的换算:
360?
=
2π
rad
180?
=
π
rad
(上述公式均可以由前面的表格由学生观察得到充分发挥表格的直观性)
6.特殊角的度数与弧度数的对应表:
度
0
30
45
120
135
150
360
弧度
(设计意图有两个方面:一是熟悉角度制与弧度制的换算,二是强化特殊角的度数与弧度数的对应关系,为以后的学习打下基础)
四、新知的应用
例1.按照下列要求,把67°30′化成弧度。
(设计意图是对角中既有度又有分该如何化成弧度?同时进一步角度制与弧度制的换算)
例2.将换算成角度(用度数表示).
(设计意图是对角中不含的实数该如何化成度?当然也为了强化角度制与弧度制的换算)
例3.利用弧度制证明下列关于扇形的公式:
其中R是半径,l是弧长,α(0<α<2π)为圆心角,S是扇形面积.
(体会弧度制下公式的简便性)
五、练习
已知扇形AOB的圆心角为120°,半径长为6,求弧AB的长及扇形AOB的
面积.
(考查对公式的掌握与应用)
六、交流展示与达标检测
(目的是反馈学生掌握情况,查找不足,加强灵活应用)
七、小结
1、由学生思考,说说通过本节课的学习,你有哪些收获?对你有什么启示?
学生甲:通过本节课的学习,我学会了什么是1弧度的角,并弄清了角度制与弧度制的关系,且能进行角度制与弧度制的互化。通过本节课的学习,使我认识到,在以后的学习中遇到问题时,多与同学合作大胆探索,在生活中遇到困难决不轻言放弃。
2、教师总结本节课所体现的教育思想和数学方法
在本节课的学习中,我们运用数学方法有讨论观察法,类比法,等价转化法,,同时也培养了同学们大胆探索、勇于合作的精神。
(注重在教学中贯穿数学思想方法,使学生体验数学思想方法在解决问题中的重要性。)
八、作业布置(略)
九、课后反思
本节课的设计思想是:在学生的探究活动中类比引入弧度制这个概念,通过小组的合作学习由特殊到一般、由易到难,既符合了学生的认知规律,又很好地突破这弧度制的概念一难点。教学中充分利用多媒体在课堂教学中的辅助作用,,使教学内容更直观、更有趣,更容易理解。本节课多次采用了合作式学习方式,这既是“课改”新教学理念,也是实施新课程的创新教学行为,这种新的学生自主学习方式,有利于问题的解决和教学目标的实现,有利于培养学生合作意识和合作技能,有利于学生之间的交流与沟通,有利于培养学生的创新精神。
1
360
y
B
B
1rad
x
A
O
O
A
PAGE
/
NUMPAGES
知识像烛光,能照亮一个人,也能照亮无数的人。--培根
知识像烛光,能照亮一个人,也能照亮无数的人。--培根
《弧度制》教学设计
教学内容:
《普通高中课程标准试验教科书·数学》必修四第一章:三角函数§1.1任意角和弧度制§1.1.2弧度制
课
题:弧度制
三维目标:
1.通过类比长度、重量的不同度量制,使学生体会一个量可以用不同的单位制来度量,从而引出弧度制。
2.理解弧度制的意义,以及任意角的弧度数与弧长半径的关系。
3.能进行角度制与弧度制的互化。
4.通过探究使学生认识到角度制与弧度都是度量角的制度,从而使学生体会到事物之间总是相互联系的。
5.通过总结引入弧度制的好处,使学生学会归纳整理并认识到任何新知识的学习,都会为解决实际问题带来方便,从而激发学生的学习兴趣。
6.通过探究任意角的弧度数与弧长半径的关系,培养学生的合作意识和创新能力。
教学重点:理解弧度制的意义,能进行角度制与弧度制的互化
教学难点:弧度制的概念及其与角度的换算
课时安排:一课时
教学过程
一、课前布置任务
完成导学案中的自主学习部分,并尝试解决其它部分内容。
二、类比引入
1.由姚明的身高引入同一对象有不同的单位表示。
(设计意图是问题来源于实际生活,可以激发学生的兴趣,使得新知识的学习自然亲切)
2.在初中几何里,我们学过角的度量,1度的角是怎样定义的呢?角还有没有新的度量方法?
(教师顺势引导点明我们这节课要学习的内容,从而引出概念,这样以旧引新,符合学生的认知规律)
三、新知探究
1.定义:把长度等于半径长的弧所对的圆心角叫做1弧度的角.用符号rad表示。
弧度制的定义:用弧度做单位来度量角的制度叫做弧度制
说明:
(1)弧度制是以“弧度”为单位来度量角的单位制,角度制是以“度”为单位来度量角的单位制;
(2)1弧度是弧长等于半径长的圆弧所对的圆心角的大小,而1度是圆周的
所对的圆心角的大小;1弧度≠1?;
(3)弧度制是十进制,它的表示是用一个实数表示,而角度制是六十进制;
(4)今后在用弧度制表示角的时候,弧度二字或rad可以略去不写。
(设计意图是剖析概念可以帮助学生很好的理解概念的内涵和外延)
探究1:一定大小的圆心角与半径大小是否有关?
将角度固定,改变半径大小,计算弧长。
(结论:一定大小的圆心角与半径大小无关,意在说明弧度制定义的合理性。)
探究2:如图,半径为r的圆的圆心与原点重合,角的始边与x轴的正半轴重合,交圆于点A,终边与圆交于点B。请在下列表格中填空。
A
B的弧长
OB旋转的方向
∠AOB的弧度数
∠AOB的度数
逆时针方向
逆时针方向
1
-2
0
(设计意图是由学生探索与发现,在合作中掌握新知识。具体做法是:将全班学生分成四组,每组填两行。每组的学生前后座4人相互讨论,然后推荐一人起来回答。教师进行巡视,引导学生进行合作学习,帮助学生解答疑惑,并对学生的回答及时进行激励性评价,激发学生探究问题的积极性。)
探究3:继续观察上述表格,看一看∠AOB的弧度数与∠AOB的度数的符号有什么关系?
(设计意图是建立角的集合于事实数集之间的一一对应关系,而这种关系在表中很容易发现。)
2.正角的弧度数为正数
负角的弧度数为负数
零角的弧度数为零
3.任一已知角的弧度数的绝对值
其中
为以角
作为圆心角时所对圆弧的长,r为圆的半径.
5.角度制与弧度制的换算:
360?
=
2π
rad
180?
=
π
rad
(上述公式均可以由前面的表格由学生观察得到充分发挥表格的直观性)
6.特殊角的度数与弧度数的对应表:
度
0
30
45
120
135
150
360
弧度
(设计意图有两个方面:一是熟悉角度制与弧度制的换算,二是强化特殊角的度数与弧度数的对应关系,为以后的学习打下基础)
四、新知的应用
例1.按照下列要求,把67°30′化成弧度。
(设计意图是对角中既有度又有分该如何化成弧度?同时进一步角度制与弧度制的换算)
例2.将换算成角度(用度数表示).
(设计意图是对角中不含的实数该如何化成度?当然也为了强化角度制与弧度制的换算)
例3.利用弧度制证明下列关于扇形的公式:
其中R是半径,l是弧长,α(0<α<2π)为圆心角,S是扇形面积.
(体会弧度制下公式的简便性)
五、练习
已知扇形AOB的圆心角为120°,半径长为6,求弧AB的长及扇形AOB的
面积.
(考查对公式的掌握与应用)
六、交流展示与达标检测
(目的是反馈学生掌握情况,查找不足,加强灵活应用)
七、小结
1、由学生思考,说说通过本节课的学习,你有哪些收获?对你有什么启示?
学生甲:通过本节课的学习,我学会了什么是1弧度的角,并弄清了角度制与弧度制的关系,且能进行角度制与弧度制的互化。通过本节课的学习,使我认识到,在以后的学习中遇到问题时,多与同学合作大胆探索,在生活中遇到困难决不轻言放弃。
2、教师总结本节课所体现的教育思想和数学方法
在本节课的学习中,我们运用数学方法有讨论观察法,类比法,等价转化法,,同时也培养了同学们大胆探索、勇于合作的精神。
(注重在教学中贯穿数学思想方法,使学生体验数学思想方法在解决问题中的重要性。)
八、作业布置(略)
九、课后反思
本节课的设计思想是:在学生的探究活动中类比引入弧度制这个概念,通过小组的合作学习由特殊到一般、由易到难,既符合了学生的认知规律,又很好地突破这弧度制的概念一难点。教学中充分利用多媒体在课堂教学中的辅助作用,,使教学内容更直观、更有趣,更容易理解。本节课多次采用了合作式学习方式,这既是“课改”新教学理念,也是实施新课程的创新教学行为,这种新的学生自主学习方式,有利于问题的解决和教学目标的实现,有利于培养学生合作意识和合作技能,有利于学生之间的交流与沟通,有利于培养学生的创新精神。
1
360
y
B
B
1rad
x
A
O
O
A
PAGE
/
NUMPAGES
