2020-2021学年人教版八年级数学下册18.2第2课时:菱形的判定(28张)
文档属性
| 名称 | 2020-2021学年人教版八年级数学下册18.2第2课时:菱形的判定(28张) |  | |
| 格式 | pptx | ||
| 文件大小 | 227.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-13 00:17:08 | ||
图片预览







文档简介
第十八章 平行四边形
18.2.2 菱 形
第2课时 菱形的判定
学习目标
1.经历菱形判定定理的探究过程,掌握菱形的判定定理.(重点)
2.能运用菱形的判定方法判定一个四边形是菱形.. (难点)
一组邻边相等
有一组邻边相等的平行四边形叫做菱形
平行四边形
菱形
复习引入
菱形的定义是什么?性质有哪些?
菱形的性质
两组对边平行
四条边相等
两组对角分别相等
邻角互补
两条对角线互相垂直平分
每一条对角线平分一组对角
边
角
对角线
(1)菱形具有平行四边形的一切性质;
(2)菱形的四条边都相等;
(3)菱形的两条对角线互相垂直,并且每一条对角
线平分一组对角;
菱形的性质
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形?
动手操作
猜想:
对角线互相垂直的平行四边形是菱形.
A
B
C
D
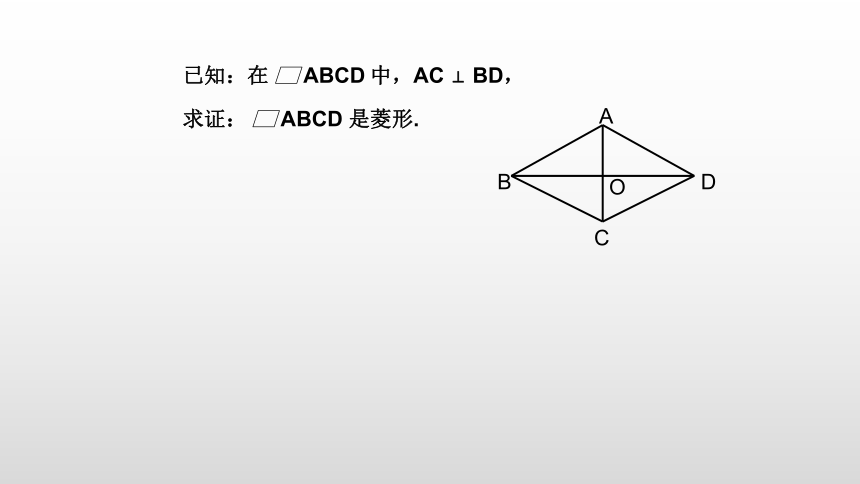
已知:在 中,AC ⊥ BD,
ABCD
ABCD
求证: 是菱形.
O
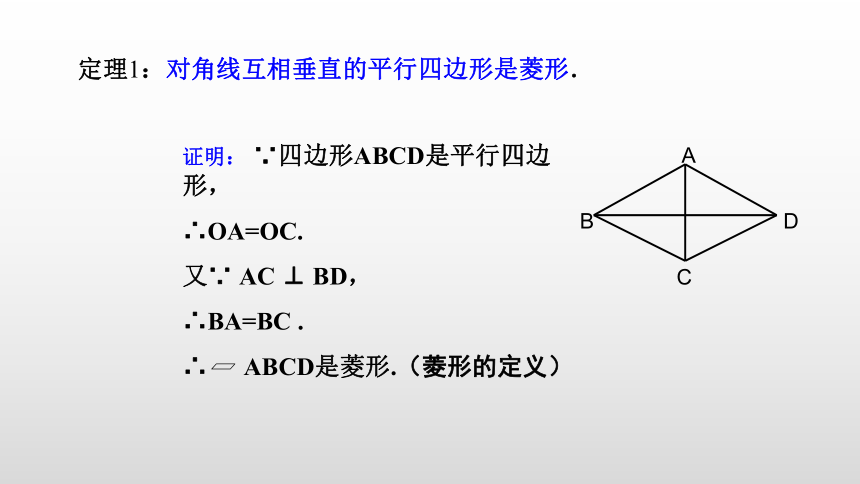
证明: ∵四边形ABCD是平行四边形,
∴OA=OC.
又∵ AC ⊥ BD,
∴BA=BC .
∴ ABCD是菱形.(菱形的定义)
A
B
C
D
定理1:对角线互相垂直的平行四边形是菱形.
提示:此方法包括两个条件——
(1)是一个平行四边形;
(2)两条对角线互相垂直.
对角线互相垂直且平分的四边形是菱形.
例 如图,□ABCD的对角线AC,BD相交于点O,且
AB=5,AO=4,BO=3.求证: □ ABCD 是菱形.
A
D
C
B
O
∵AB=5,AO=4,BO=3,
∴AB2=AO2+BO2.
∴△OAB是直角三角形,
AC⊥BD.
∴□ABCD 是菱形.
证明:
在四边形ABCD中,对角线AC,BD互相平分,若添加一个条件使得四边形ABCD是菱形,则这个条件可以是 ( )
A.∠ABC=90°
B.AC⊥BD
C.AB=CD
D.AB∥CD
B
命题2:四条边都相等的四边形是菱形.
已知:四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.
A
D
C
B
O
证明:∵ AB=BC=CD=AD,
∴四边形ABCD是平行四边形.
又AB=BC,
∴ ABCD是菱形.
已知:如图,在△ABC中, AD是角平分线,点E、F分别在AB、 AD上,且AE=AC,EF = ED.求证:四边形CDEF是菱形.
证明: ∵ ∠1= ∠2,
又∵AE=AC,
∴ △ACD≌ △AED (SAS).
同理△ACF≌△AEF(SAS) .
∴CD=ED, CF=EF.
又∵EF=ED,
∴四边形ABCD是菱形(四边相等的四边形是菱形).
2
A
C
E
D
F
1
B
有一组邻边相等的平行四边形叫做菱形
对角线互相垂直的平行四边形是菱形
有四条边相等的四边形是菱形
+ 邻边相等 =
+对角线线互相垂直 =
四条边相等 + =
菱形的判定方法
知识巩固
1.如图,四边形 ABCD 是轴对称图形,且直线 AC 是对称轴,BD与AC交于点O,AB∥CD,则下列结论:
①AC⊥BD;②AD∥ BC;
③四边形 ABCD 是菱形;
④△ABD≌△CDB.
其中正确的是____________(只填写序号).
①②③④
A
D
C
B
O
2.一边长为5cm平行四边形的两条对角线的长分别为24cm
和26cm,那么平行四边形的面积是 .
3.如图,将△ABC沿BC方向平移得到△DCE,连接AD,下
列条件能够判定四边形ACED为菱形的是( )
A.AB=BC B.AC=BC C.∠B=60° D.∠ACB=60°
B
A
B
D
E
C
4.一个平行四边形的一条边长是9,两条对角线的长分别是12和6 ,这是一个特殊的平行四边形吗?为什么?求出它的面积.
5 如图,四边形ABCD的四边相等,且面积为120 cm2,对角线AC =24 cm,则四边形ABCD的周长为 ( )
A.52 cm
B.40 cm
C.39 cm
D.26 cm
A
A
B
D
C
6.如图,△ABC中,AC的垂直平分线MN交AB于点D,交AC于点O,CE∥AB交MN于点E,连接AE、CD.
求证:四边形ADCE是菱形
A
D
O
E
M
证明:∵MN是AC的垂直平分线,
∴AE=CE,AD=CD,OA=OC,∠AOD=∠EOC=90°.
∵CE∥AB,
∴∠DAO=∠ECO,
∴△ADO≌△CEO(ASA).
∴AD=CE,OD=OE,
∵OD=OE,OA=OC,∴四边形ADCE是平行四边形
又∵∠AOD=90°,∴四边形ADCE是菱形.
7、判断题
(1)对角线互相垂直的四边形是菱形( )
(2)一条对角线垂直另一条对角线的四边形是菱形( )
(3)对角线互相垂直且平分的四边形是菱形( )
(4)对角线相等的四边形是菱形( )
(5)对角线互相平分且邻边相等的四边形是菱形( )
(6)两组对边分别平行且一组邻边相等的四边形是菱形( )
×
√
×
×
√
√
如图,将矩形纸片ABCD沿EF折叠,使D与B重合,折痕为EF,然后展开,连接DF,BE.
(1)求证:四边形EBFD是菱形;
(2)已知AB=3,AD=9,求折痕EF的长
拓展提升
解析:(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DEF=∠BFE,
由折叠的性质得:BE=DE,∠BEF=∠DEF,
∴∠BEF=∠BFE,
∴BE=BF,
∴DE=BF,
∵DE∥BF,
∴四边形EBFD是平行四边形,
又∵BE=DE,
∴四边形EBFD是菱形;
解析:(2)解:由(1)得:四边形EBFD是菱形,
∴BF=BE,
设BE=x,则BF=DE=BE=x,AE=AD-DE=9-x
在Rt△ABE中,AB2+AE2=BE2,
则32+(9-x)2=x2,
解得:x=5.
∴BF=BE=5,AE=4,
作EM⊥BC于M,
如图所示,则EM=AB=3,BM=AE=4,
∴MF=BF-BM=1,
∴EF=EM2+MF2?=32+12?=10.
?
通过今天的学习,
能说说你的收获和体会吗?
你有什么经验与收获让同学们共享呢?
回顾与反思
18.2.2 菱 形
第2课时 菱形的判定
学习目标
1.经历菱形判定定理的探究过程,掌握菱形的判定定理.(重点)
2.能运用菱形的判定方法判定一个四边形是菱形.. (难点)
一组邻边相等
有一组邻边相等的平行四边形叫做菱形
平行四边形
菱形
复习引入
菱形的定义是什么?性质有哪些?
菱形的性质
两组对边平行
四条边相等
两组对角分别相等
邻角互补
两条对角线互相垂直平分
每一条对角线平分一组对角
边
角
对角线
(1)菱形具有平行四边形的一切性质;
(2)菱形的四条边都相等;
(3)菱形的两条对角线互相垂直,并且每一条对角
线平分一组对角;
菱形的性质
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形?
动手操作
猜想:
对角线互相垂直的平行四边形是菱形.
A
B
C
D
已知:在 中,AC ⊥ BD,
ABCD
ABCD
求证: 是菱形.
O
证明: ∵四边形ABCD是平行四边形,
∴OA=OC.
又∵ AC ⊥ BD,
∴BA=BC .
∴ ABCD是菱形.(菱形的定义)
A
B
C
D
定理1:对角线互相垂直的平行四边形是菱形.
提示:此方法包括两个条件——
(1)是一个平行四边形;
(2)两条对角线互相垂直.
对角线互相垂直且平分的四边形是菱形.
例 如图,□ABCD的对角线AC,BD相交于点O,且
AB=5,AO=4,BO=3.求证: □ ABCD 是菱形.
A
D
C
B
O
∵AB=5,AO=4,BO=3,
∴AB2=AO2+BO2.
∴△OAB是直角三角形,
AC⊥BD.
∴□ABCD 是菱形.
证明:
在四边形ABCD中,对角线AC,BD互相平分,若添加一个条件使得四边形ABCD是菱形,则这个条件可以是 ( )
A.∠ABC=90°
B.AC⊥BD
C.AB=CD
D.AB∥CD
B
命题2:四条边都相等的四边形是菱形.
已知:四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.
A
D
C
B
O
证明:∵ AB=BC=CD=AD,
∴四边形ABCD是平行四边形.
又AB=BC,
∴ ABCD是菱形.
已知:如图,在△ABC中, AD是角平分线,点E、F分别在AB、 AD上,且AE=AC,EF = ED.求证:四边形CDEF是菱形.
证明: ∵ ∠1= ∠2,
又∵AE=AC,
∴ △ACD≌ △AED (SAS).
同理△ACF≌△AEF(SAS) .
∴CD=ED, CF=EF.
又∵EF=ED,
∴四边形ABCD是菱形(四边相等的四边形是菱形).
2
A
C
E
D
F
1
B
有一组邻边相等的平行四边形叫做菱形
对角线互相垂直的平行四边形是菱形
有四条边相等的四边形是菱形
+ 邻边相等 =
+对角线线互相垂直 =
四条边相等 + =
菱形的判定方法
知识巩固
1.如图,四边形 ABCD 是轴对称图形,且直线 AC 是对称轴,BD与AC交于点O,AB∥CD,则下列结论:
①AC⊥BD;②AD∥ BC;
③四边形 ABCD 是菱形;
④△ABD≌△CDB.
其中正确的是____________(只填写序号).
①②③④
A
D
C
B
O
2.一边长为5cm平行四边形的两条对角线的长分别为24cm
和26cm,那么平行四边形的面积是 .
3.如图,将△ABC沿BC方向平移得到△DCE,连接AD,下
列条件能够判定四边形ACED为菱形的是( )
A.AB=BC B.AC=BC C.∠B=60° D.∠ACB=60°
B
A
B
D
E
C
4.一个平行四边形的一条边长是9,两条对角线的长分别是12和6 ,这是一个特殊的平行四边形吗?为什么?求出它的面积.
5 如图,四边形ABCD的四边相等,且面积为120 cm2,对角线AC =24 cm,则四边形ABCD的周长为 ( )
A.52 cm
B.40 cm
C.39 cm
D.26 cm
A
A
B
D
C
6.如图,△ABC中,AC的垂直平分线MN交AB于点D,交AC于点O,CE∥AB交MN于点E,连接AE、CD.
求证:四边形ADCE是菱形
A
D
O
E
M
证明:∵MN是AC的垂直平分线,
∴AE=CE,AD=CD,OA=OC,∠AOD=∠EOC=90°.
∵CE∥AB,
∴∠DAO=∠ECO,
∴△ADO≌△CEO(ASA).
∴AD=CE,OD=OE,
∵OD=OE,OA=OC,∴四边形ADCE是平行四边形
又∵∠AOD=90°,∴四边形ADCE是菱形.
7、判断题
(1)对角线互相垂直的四边形是菱形( )
(2)一条对角线垂直另一条对角线的四边形是菱形( )
(3)对角线互相垂直且平分的四边形是菱形( )
(4)对角线相等的四边形是菱形( )
(5)对角线互相平分且邻边相等的四边形是菱形( )
(6)两组对边分别平行且一组邻边相等的四边形是菱形( )
×
√
×
×
√
√
如图,将矩形纸片ABCD沿EF折叠,使D与B重合,折痕为EF,然后展开,连接DF,BE.
(1)求证:四边形EBFD是菱形;
(2)已知AB=3,AD=9,求折痕EF的长
拓展提升
解析:(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DEF=∠BFE,
由折叠的性质得:BE=DE,∠BEF=∠DEF,
∴∠BEF=∠BFE,
∴BE=BF,
∴DE=BF,
∵DE∥BF,
∴四边形EBFD是平行四边形,
又∵BE=DE,
∴四边形EBFD是菱形;
解析:(2)解:由(1)得:四边形EBFD是菱形,
∴BF=BE,
设BE=x,则BF=DE=BE=x,AE=AD-DE=9-x
在Rt△ABE中,AB2+AE2=BE2,
则32+(9-x)2=x2,
解得:x=5.
∴BF=BE=5,AE=4,
作EM⊥BC于M,
如图所示,则EM=AB=3,BM=AE=4,
∴MF=BF-BM=1,
∴EF=EM2+MF2?=32+12?=10.
?
通过今天的学习,
能说说你的收获和体会吗?
你有什么经验与收获让同学们共享呢?
回顾与反思
