2020--2021学年苏科版七年级数学下学期 7.1 探索直线平行的条件 同步练习(Word版 含答案)
文档属性
| 名称 | 2020--2021学年苏科版七年级数学下学期 7.1 探索直线平行的条件 同步练习(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 91.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-13 16:27:29 | ||
图片预览

文档简介
7.1 探索直线平行的条件
一.选择题
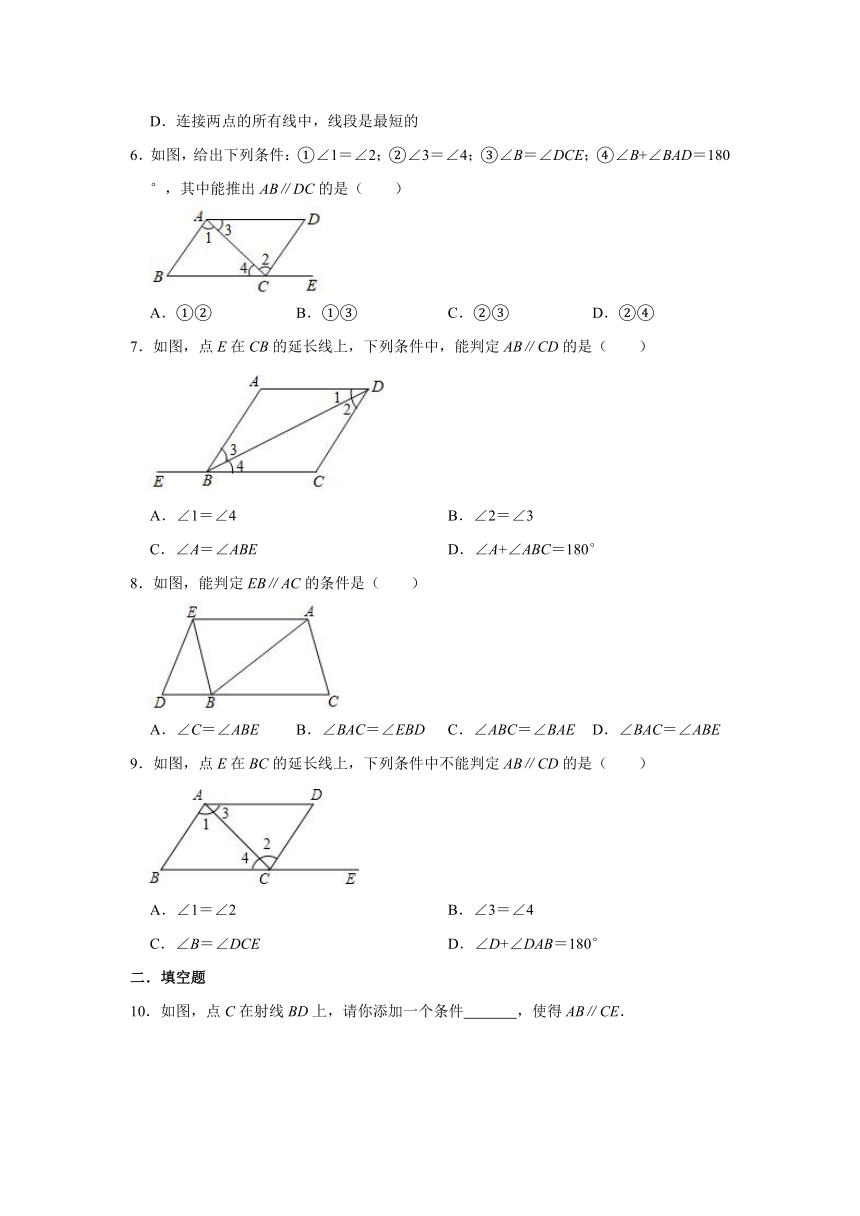
1.如图,能判定AB∥EF的条件是( )
A.∠ABD=∠FEC B.∠ABC=∠FEC C.∠DBC=∠FEB D.∠DBC=∠FEC
2.如图,BD平分∠ABC,若∠1=∠2,则( )
A.AB∥CD B.AD∥BC C.AD=BC D.AB=CD
3.如图所示,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
A.∠3=∠A B.∠1=∠2
C.∠D=∠DCE D.∠D+∠ACD=180°
4.如图,若∠1=∠2,则下列选项中可以判定AB∥CD的是( )
A. B.
C. D.
5.下列说法中正确的是( )
A.过直线外一点有两条直线平行于已知直线
B.若两个角的顶点重合,那么这两个角是对顶角
C.一条射线把一个角分成两个角,那么这条射线是角的平分线
D.连接两点的所有线中,线段是最短的
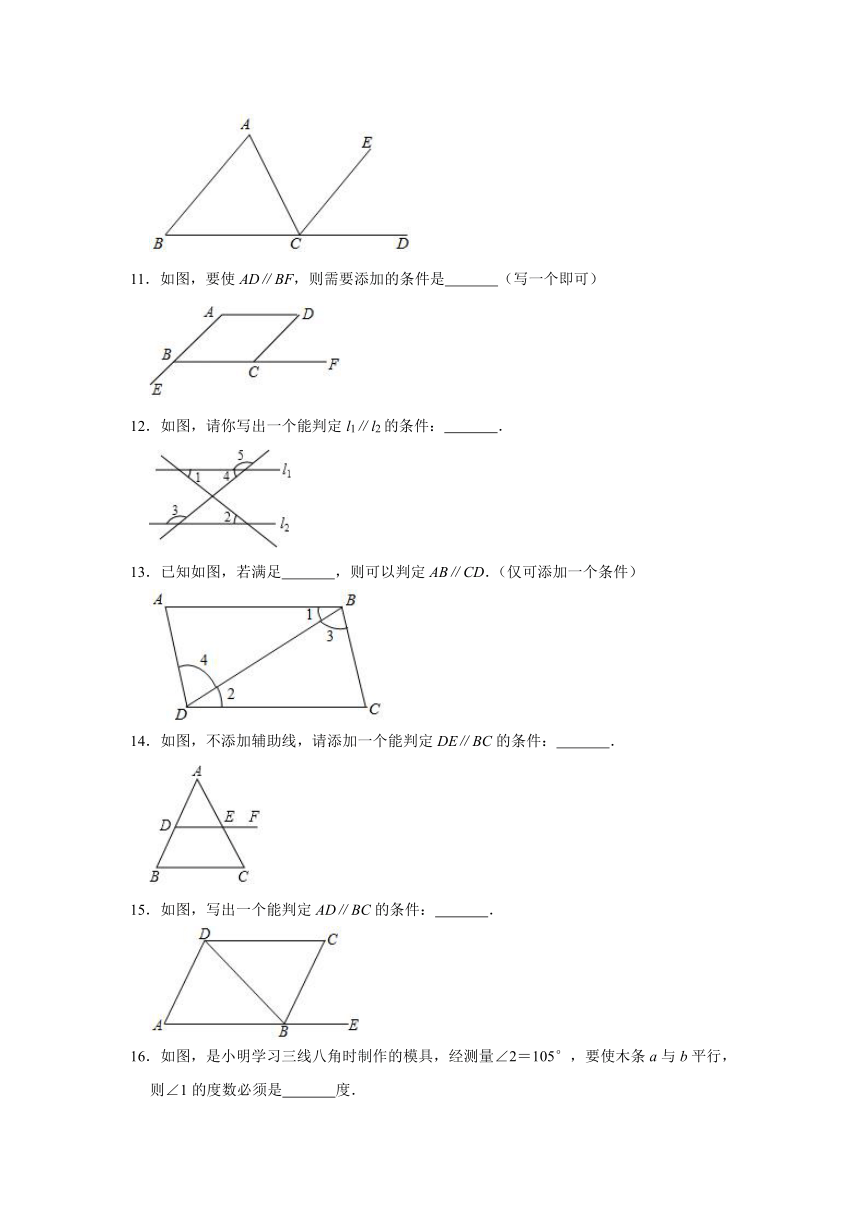
6.如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠DCE;④∠B+∠BAD=180°,其中能推出AB∥DC的是( )
A.①② B.①③ C.②③ D.②④
7.如图,点E在CB的延长线上,下列条件中,能判定AB∥CD的是( )
A.∠1=∠4 B.∠2=∠3
C.∠A=∠ABE D.∠A+∠ABC=180°
8.如图,能判定EB∥AC的条件是( )
A.∠C=∠ABE B.∠BAC=∠EBD C.∠ABC=∠BAE D.∠BAC=∠ABE
9.如图,点E在BC的延长线上,下列条件中不能判定AB∥CD的是( )
A.∠1=∠2 B.∠3=∠4
C.∠B=∠DCE D.∠D+∠DAB=180°
二.填空题
10.如图,点C在射线BD上,请你添加一个条件 ,使得AB∥CE.
11.如图,要使AD∥BF,则需要添加的条件是 (写一个即可)
12.如图,请你写出一个能判定l1∥l2的条件: .
13.已知如图,若满足 ,则可以判定AB∥CD.(仅可添加一个条件)
14.如图,不添加辅助线,请添加一个能判定DE∥BC的条件: .
15.如图,写出一个能判定AD∥BC的条件: .
16.如图,是小明学习三线八角时制作的模具,经测量∠2=105°,要使木条a与b平行,则∠1的度数必须是 度.
三.解答题
17.两条直线被第三条直线所截,∠1是∠2的同旁内角,∠2是∠3的内错角.
(1)画出示意图,标出∠1,∠2,∠3.
(2)若∠1=2∠2,∠2=2∠3,求∠3的度数.
18.如图所示,把一根筷子一端放在水里,一端露出水面,筷子变弯了,它真的弯了吗?其实没有,这是光的折射现象,光从空气中射入水中,光的传播方向发生了改变.
(1)请指出与∠1是同旁内角的有哪些角?请指出与∠2是内错角的有哪些角?
(2)若∠1=115°,测得∠BOM=145°,从水面上看斜插入水中的筷子,水下部分向上折弯了多少度?请说明理由.
19.如图,直线DE经过点A.
(1)写出∠B的内错角是 ,同旁内角是 .
(2)若∠EAC=∠C,AC平分∠BAE,∠B=44°,求∠C的度数.
参考答案
一.选择题
1. B.
2. B.
3. B.
4. D.
5. D.
6. B.
7. B.
8. D.
9. B.
二.填空题
10.∠B=∠ECD或∠B+∠BCE=180°或∠A=∠ACE.
11.∠A=∠EBC(答案不唯一).
12.∠1=∠2或∠3=∠5或∠3+∠4=180°.
13.∠1=∠2(答案不唯一).
14.∠ADE=∠B(答案不唯一).
15.∠A=∠CBE(答案不唯一).
16. 75.
三.解答题
17.解:(1)如图所示:
(2)∵∠1=2∠2,∠2=2∠3,
∴设∠3=x,则∠2=2x,∠1=4x,
∵∠1+∠3=180°,
∴x+4x=180°,
解得:x=36°,
故∠3=36°.
18.解:(1)与∠1是同旁内角的有∠AOE,∠MOE,∠ADE;
与∠2是内错角的有∠MOE,∠AOE;
(2)∵AB∥CD,
∴∠BOE=∠1=115°,
∵∠BOM=145°,
∴∠MOE=∠BOM﹣∠BOE=145°﹣115°=30°,
∴向上折弯了30°.
19.解:(1)∠B的内错角是∠BAD,∠B的同旁内角是∠BAC,∠EAB和∠C;
(2)∵∠EAC=∠C,
∴DE∥BC,
∴∠BAE=180°﹣44°=136°,
∵AC平分∠BAE,
∴∠EAC=68°,
∴∠C=∠EAC=68°,
故答案为:∠BAD;∠BAC,∠EAB和∠C
一.选择题
1.如图,能判定AB∥EF的条件是( )
A.∠ABD=∠FEC B.∠ABC=∠FEC C.∠DBC=∠FEB D.∠DBC=∠FEC
2.如图,BD平分∠ABC,若∠1=∠2,则( )
A.AB∥CD B.AD∥BC C.AD=BC D.AB=CD
3.如图所示,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
A.∠3=∠A B.∠1=∠2
C.∠D=∠DCE D.∠D+∠ACD=180°
4.如图,若∠1=∠2,则下列选项中可以判定AB∥CD的是( )
A. B.
C. D.
5.下列说法中正确的是( )
A.过直线外一点有两条直线平行于已知直线
B.若两个角的顶点重合,那么这两个角是对顶角
C.一条射线把一个角分成两个角,那么这条射线是角的平分线
D.连接两点的所有线中,线段是最短的
6.如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠DCE;④∠B+∠BAD=180°,其中能推出AB∥DC的是( )
A.①② B.①③ C.②③ D.②④
7.如图,点E在CB的延长线上,下列条件中,能判定AB∥CD的是( )
A.∠1=∠4 B.∠2=∠3
C.∠A=∠ABE D.∠A+∠ABC=180°
8.如图,能判定EB∥AC的条件是( )
A.∠C=∠ABE B.∠BAC=∠EBD C.∠ABC=∠BAE D.∠BAC=∠ABE
9.如图,点E在BC的延长线上,下列条件中不能判定AB∥CD的是( )
A.∠1=∠2 B.∠3=∠4
C.∠B=∠DCE D.∠D+∠DAB=180°
二.填空题
10.如图,点C在射线BD上,请你添加一个条件 ,使得AB∥CE.
11.如图,要使AD∥BF,则需要添加的条件是 (写一个即可)
12.如图,请你写出一个能判定l1∥l2的条件: .
13.已知如图,若满足 ,则可以判定AB∥CD.(仅可添加一个条件)
14.如图,不添加辅助线,请添加一个能判定DE∥BC的条件: .
15.如图,写出一个能判定AD∥BC的条件: .
16.如图,是小明学习三线八角时制作的模具,经测量∠2=105°,要使木条a与b平行,则∠1的度数必须是 度.
三.解答题
17.两条直线被第三条直线所截,∠1是∠2的同旁内角,∠2是∠3的内错角.
(1)画出示意图,标出∠1,∠2,∠3.
(2)若∠1=2∠2,∠2=2∠3,求∠3的度数.
18.如图所示,把一根筷子一端放在水里,一端露出水面,筷子变弯了,它真的弯了吗?其实没有,这是光的折射现象,光从空气中射入水中,光的传播方向发生了改变.
(1)请指出与∠1是同旁内角的有哪些角?请指出与∠2是内错角的有哪些角?
(2)若∠1=115°,测得∠BOM=145°,从水面上看斜插入水中的筷子,水下部分向上折弯了多少度?请说明理由.
19.如图,直线DE经过点A.
(1)写出∠B的内错角是 ,同旁内角是 .
(2)若∠EAC=∠C,AC平分∠BAE,∠B=44°,求∠C的度数.
参考答案
一.选择题
1. B.
2. B.
3. B.
4. D.
5. D.
6. B.
7. B.
8. D.
9. B.
二.填空题
10.∠B=∠ECD或∠B+∠BCE=180°或∠A=∠ACE.
11.∠A=∠EBC(答案不唯一).
12.∠1=∠2或∠3=∠5或∠3+∠4=180°.
13.∠1=∠2(答案不唯一).
14.∠ADE=∠B(答案不唯一).
15.∠A=∠CBE(答案不唯一).
16. 75.
三.解答题
17.解:(1)如图所示:
(2)∵∠1=2∠2,∠2=2∠3,
∴设∠3=x,则∠2=2x,∠1=4x,
∵∠1+∠3=180°,
∴x+4x=180°,
解得:x=36°,
故∠3=36°.
18.解:(1)与∠1是同旁内角的有∠AOE,∠MOE,∠ADE;
与∠2是内错角的有∠MOE,∠AOE;
(2)∵AB∥CD,
∴∠BOE=∠1=115°,
∵∠BOM=145°,
∴∠MOE=∠BOM﹣∠BOE=145°﹣115°=30°,
∴向上折弯了30°.
19.解:(1)∠B的内错角是∠BAD,∠B的同旁内角是∠BAC,∠EAB和∠C;
(2)∵∠EAC=∠C,
∴DE∥BC,
∴∠BAE=180°﹣44°=136°,
∵AC平分∠BAE,
∴∠EAC=68°,
∴∠C=∠EAC=68°,
故答案为:∠BAD;∠BAC,∠EAB和∠C
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
