2020-2021学年九年级数学人教版下册第27章 相似 单元练习卷(Word版 含答案)
文档属性
| 名称 | 2020-2021学年九年级数学人教版下册第27章 相似 单元练习卷(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 139.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-13 16:37:29 | ||
图片预览

文档简介
第27章 相似
一.选择题
1.如果2a=5b(a,b均不为0),那么下列比例式中正确的是( )
A.= B.= C.= D.=
2.如果C是线段AB延长线上一点,且AC:BC=3:1,那么AB:BC等于( )
A.2:1 B.1:2 C.4:1 D.1:4
3.如图,乐器上的一根弦AB=80cm,两个端点A,B固定在乐器板面上,支撑点C是靠近点B的黄金分割点,支撑点D是靠近点A的黄金分割点,则C,D之间的距离为( )
A.(40﹣40)cm B.(80﹣40)cm
C.(120﹣40)cm D.(80﹣160)cm
4.如图,点D、E分别在△ABC的边AB、AC上,下列各比例式不一定能推得DE∥BC的是( )
A.= B.= C.= D.=
5.下列图形中一定是相似形的是( )
A.两个等边三角形 B.两个菱形
C.两个矩形 D.两个直角三角形
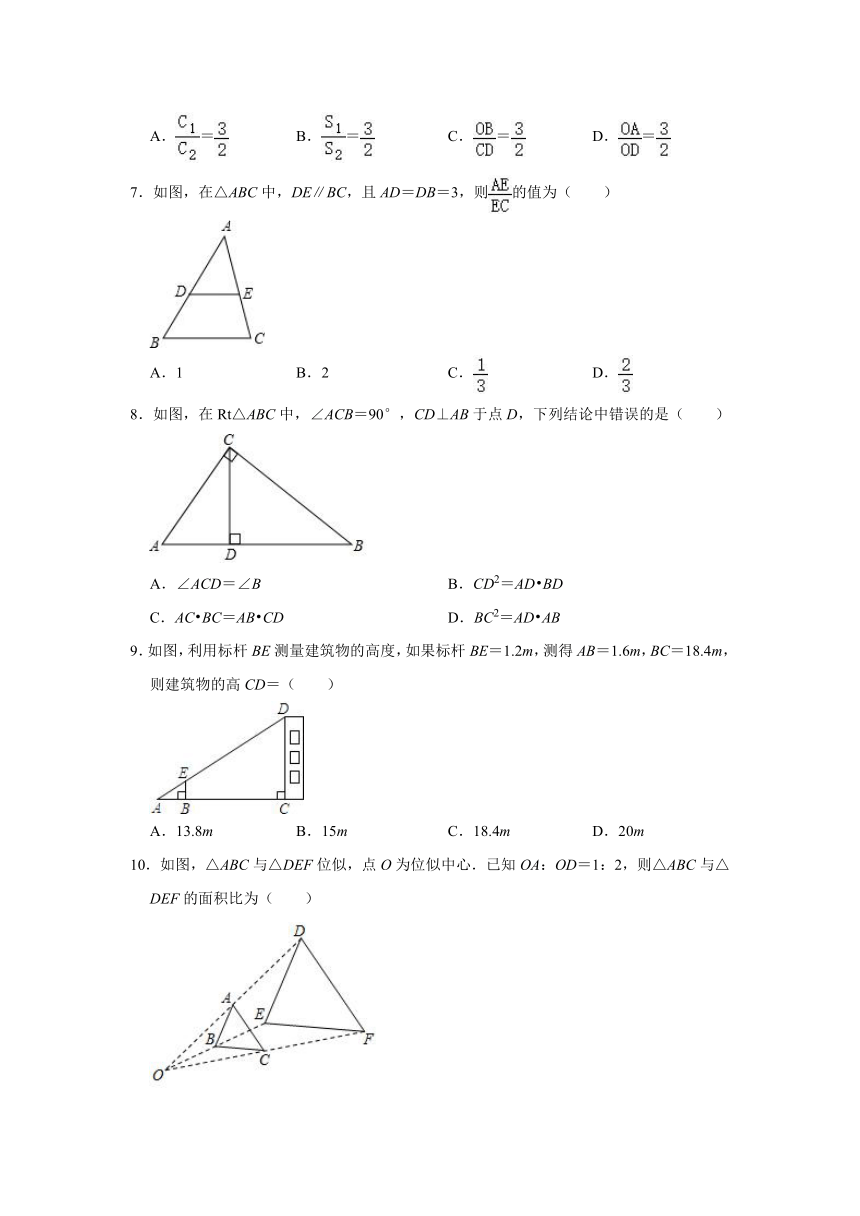
6.如图,△OAB∽△OCD,OA:OC=3:2,△OAB与△OCD的面积分别是S1与S2,周长分别是C1与C2,则下列说法正确的是( )
A.= B.= C.= D.=
7.如图,在△ABC中,DE∥BC,且AD=DB=3,则的值为( )
A.1 B.2 C. D.
8.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,下列结论中错误的是( )
A.∠ACD=∠B B.CD2=AD?BD
C.AC?BC=AB?CD D.BC2=AD?AB
9.如图,利用标杆BE测量建筑物的高度,如果标杆BE=1.2m,测得AB=1.6m,BC=18.4m,则建筑物的高CD=( )
A.13.8m B.15m C.18.4m D.20m
10.如图,△ABC与△DEF位似,点O为位似中心.已知OA:OD=1:2,则△ABC与△DEF的面积比为( )
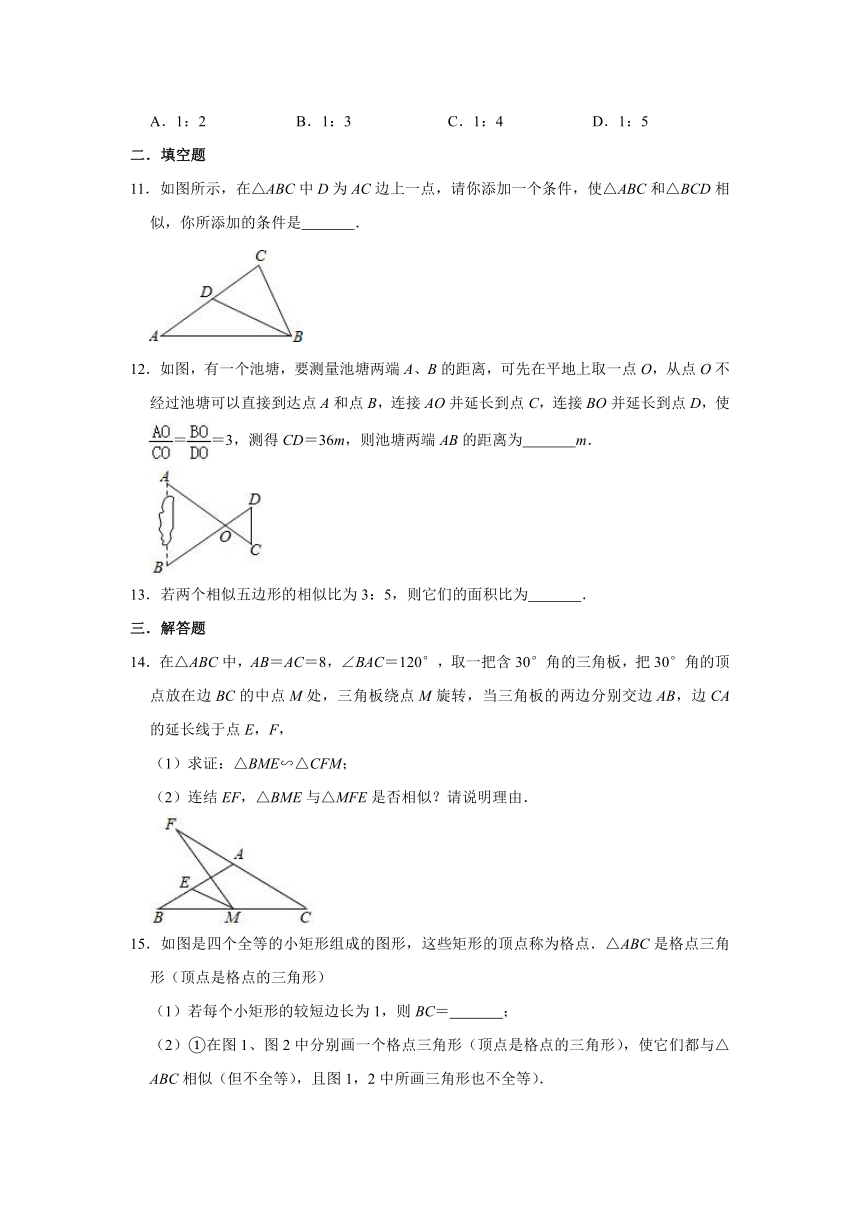
A.1:2 B.1:3 C.1:4 D.1:5
二.填空题
11.如图所示,在△ABC中D为AC边上一点,请你添加一个条件,使△ABC和△BCD相似,你所添加的条件是 .
12.如图,有一个池塘,要测量池塘两端A、B的距离,可先在平地上取一点O,从点O不经过池塘可以直接到达点A和点B,连接AO并延长到点C,连接BO并延长到点D,使==3,测得CD=36m,则池塘两端AB的距离为 m.
13.若两个相似五边形的相似比为3:5,则它们的面积比为 .
三.解答题
14.在△ABC中,AB=AC=8,∠BAC=120°,取一把含30°角的三角板,把30°角的顶点放在边BC的中点M处,三角板绕点M旋转,当三角板的两边分别交边AB,边CA的延长线于点E,F,
(1)求证:△BME∽△CFM;
(2)连结EF,△BME与△MFE是否相似?请说明理由.
15.如图是四个全等的小矩形组成的图形,这些矩形的顶点称为格点.△ABC是格点三角形(顶点是格点的三角形)
(1)若每个小矩形的较短边长为1,则BC= ;
(2)①在图1、图2中分别画一个格点三角形(顶点是格点的三角形),使它们都与△ABC相似(但不全等),且图1,2中所画三角形也不全等).
②在图3中只用直尺(没有刻度)画出△ABC的重心M.(保留痕迹,点M用黑点表示,并注上字母M)
16.如图,在平面直角坐标系中,△ABC的顶点坐标分别是A(﹣2,3),B(﹣3,2),C(﹣1,1).
(1)以坐标原点O为位似中心,﹣2为位似比.将△ABC放大,得到△A'B'C′.请在平面直角坐标系中画出△A'B'C';
(2)求出△A'B'C的面积.
参考答案
一.选择题
1. C.
2. A.
3. D.
4. B.
5. A.
6. A.
7. A.
8. D.
9. B.
10. C.
二.填空题
11.∠A=∠CBD或∠CDB=∠ABC(答案不唯一).
12. 108.
13. 9:25.
三.解答题
14.(1)证明:如图,
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°.
∵∠EMC=∠B+∠BEM=∠EMF+∠FMC,∠B=∠EMF=30°,
∴∠BEM=∠FMC,
∴△BME∽△CFM.
(2)解:△BME与△MFE相似,理由如下:
∵△BME∽△CFM,
∴=.
∵BM=CM,
∴=.
∵∠B=∠EMF=30°,
∴△BME∽△MFE.
15.解:(1)BC==;
故答案为:;
(2)①如图1,2所示:△A′B′C′,△A″B″C″即为所求;
②如图3所示:M即为所求.
16.解:(1)如图,△A'B'C'为所作;
(2)△A'B'C的面积=4S△ABC=4(2×2﹣×1×1﹣×1×2﹣×1×2)=6.
一.选择题
1.如果2a=5b(a,b均不为0),那么下列比例式中正确的是( )
A.= B.= C.= D.=
2.如果C是线段AB延长线上一点,且AC:BC=3:1,那么AB:BC等于( )
A.2:1 B.1:2 C.4:1 D.1:4
3.如图,乐器上的一根弦AB=80cm,两个端点A,B固定在乐器板面上,支撑点C是靠近点B的黄金分割点,支撑点D是靠近点A的黄金分割点,则C,D之间的距离为( )
A.(40﹣40)cm B.(80﹣40)cm
C.(120﹣40)cm D.(80﹣160)cm
4.如图,点D、E分别在△ABC的边AB、AC上,下列各比例式不一定能推得DE∥BC的是( )
A.= B.= C.= D.=
5.下列图形中一定是相似形的是( )
A.两个等边三角形 B.两个菱形
C.两个矩形 D.两个直角三角形
6.如图,△OAB∽△OCD,OA:OC=3:2,△OAB与△OCD的面积分别是S1与S2,周长分别是C1与C2,则下列说法正确的是( )
A.= B.= C.= D.=
7.如图,在△ABC中,DE∥BC,且AD=DB=3,则的值为( )
A.1 B.2 C. D.
8.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,下列结论中错误的是( )
A.∠ACD=∠B B.CD2=AD?BD
C.AC?BC=AB?CD D.BC2=AD?AB
9.如图,利用标杆BE测量建筑物的高度,如果标杆BE=1.2m,测得AB=1.6m,BC=18.4m,则建筑物的高CD=( )
A.13.8m B.15m C.18.4m D.20m
10.如图,△ABC与△DEF位似,点O为位似中心.已知OA:OD=1:2,则△ABC与△DEF的面积比为( )
A.1:2 B.1:3 C.1:4 D.1:5
二.填空题
11.如图所示,在△ABC中D为AC边上一点,请你添加一个条件,使△ABC和△BCD相似,你所添加的条件是 .
12.如图,有一个池塘,要测量池塘两端A、B的距离,可先在平地上取一点O,从点O不经过池塘可以直接到达点A和点B,连接AO并延长到点C,连接BO并延长到点D,使==3,测得CD=36m,则池塘两端AB的距离为 m.
13.若两个相似五边形的相似比为3:5,则它们的面积比为 .
三.解答题
14.在△ABC中,AB=AC=8,∠BAC=120°,取一把含30°角的三角板,把30°角的顶点放在边BC的中点M处,三角板绕点M旋转,当三角板的两边分别交边AB,边CA的延长线于点E,F,
(1)求证:△BME∽△CFM;
(2)连结EF,△BME与△MFE是否相似?请说明理由.
15.如图是四个全等的小矩形组成的图形,这些矩形的顶点称为格点.△ABC是格点三角形(顶点是格点的三角形)
(1)若每个小矩形的较短边长为1,则BC= ;
(2)①在图1、图2中分别画一个格点三角形(顶点是格点的三角形),使它们都与△ABC相似(但不全等),且图1,2中所画三角形也不全等).
②在图3中只用直尺(没有刻度)画出△ABC的重心M.(保留痕迹,点M用黑点表示,并注上字母M)
16.如图,在平面直角坐标系中,△ABC的顶点坐标分别是A(﹣2,3),B(﹣3,2),C(﹣1,1).
(1)以坐标原点O为位似中心,﹣2为位似比.将△ABC放大,得到△A'B'C′.请在平面直角坐标系中画出△A'B'C';
(2)求出△A'B'C的面积.
参考答案
一.选择题
1. C.
2. A.
3. D.
4. B.
5. A.
6. A.
7. A.
8. D.
9. B.
10. C.
二.填空题
11.∠A=∠CBD或∠CDB=∠ABC(答案不唯一).
12. 108.
13. 9:25.
三.解答题
14.(1)证明:如图,
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°.
∵∠EMC=∠B+∠BEM=∠EMF+∠FMC,∠B=∠EMF=30°,
∴∠BEM=∠FMC,
∴△BME∽△CFM.
(2)解:△BME与△MFE相似,理由如下:
∵△BME∽△CFM,
∴=.
∵BM=CM,
∴=.
∵∠B=∠EMF=30°,
∴△BME∽△MFE.
15.解:(1)BC==;
故答案为:;
(2)①如图1,2所示:△A′B′C′,△A″B″C″即为所求;
②如图3所示:M即为所求.
16.解:(1)如图,△A'B'C'为所作;
(2)△A'B'C的面积=4S△ABC=4(2×2﹣×1×1﹣×1×2﹣×1×2)=6.
