2020-2021学年北师大版七年级数学下学期 1.5 平方差公式 同步练习卷(Word版 含答案)
文档属性
| 名称 | 2020-2021学年北师大版七年级数学下学期 1.5 平方差公式 同步练习卷(Word版 含答案) | 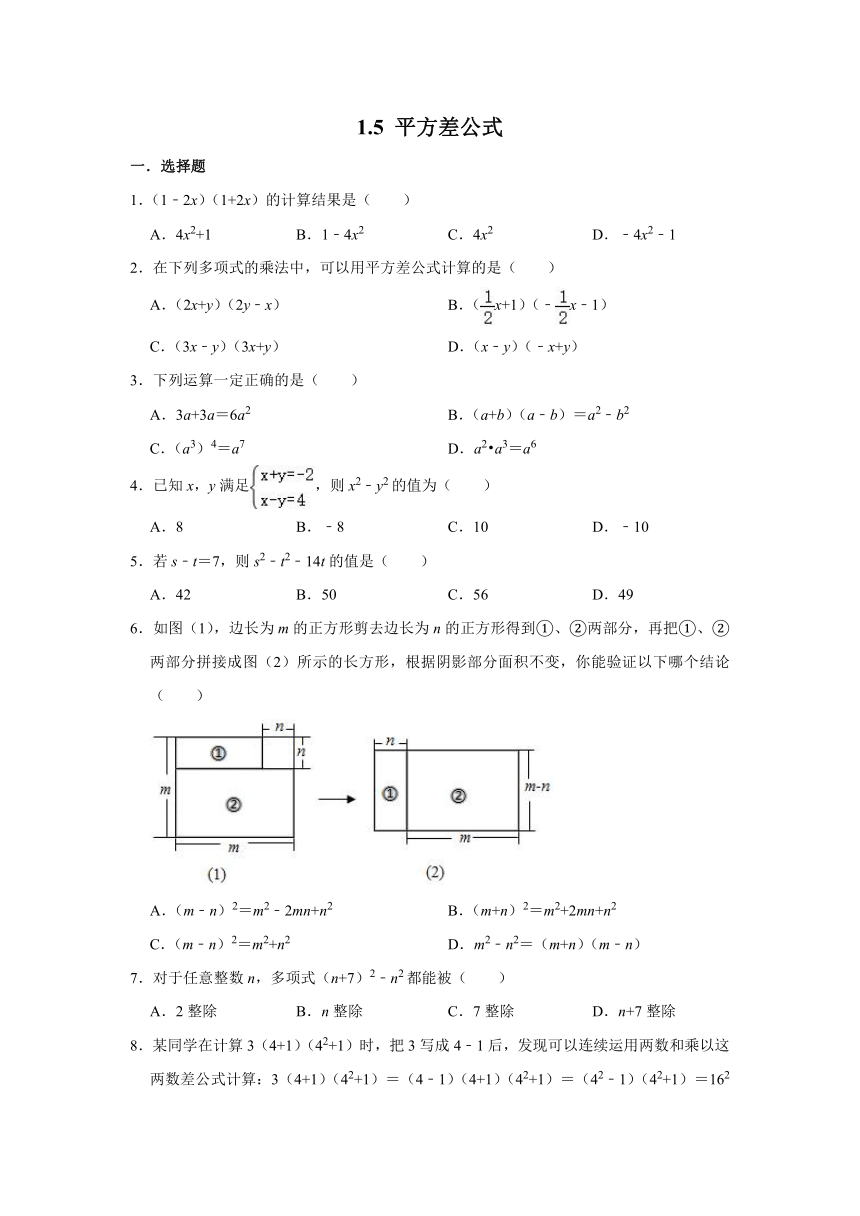 | |
| 格式 | doc | ||
| 文件大小 | 38.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-13 16:40:58 | ||
图片预览


文档简介
1.5 平方差公式
一.选择题
1.(1﹣2x)(1+2x)的计算结果是( )
A.4x2+1 B.1﹣4x2 C.4x2 D.﹣4x2﹣1
2.在下列多项式的乘法中,可以用平方差公式计算的是( )
A.(2x+y)(2y﹣x) B.(x+1)(﹣x﹣1)
C.(3x﹣y)(3x+y) D.(x﹣y)(﹣x+y)
3.下列运算一定正确的是( )
A.3a+3a=6a2 B.(a+b)(a﹣b)=a2﹣b2
C.(a3)4=a7 D.a2?a3=a6
4.已知x,y满足,则x2﹣y2的值为( )
A.8 B.﹣8 C.10 D.﹣10
5.若s﹣t=7,则s2﹣t2﹣14t的值是( )
A.42 B.50 C.56 D.49
6.如图(1),边长为m的正方形剪去边长为n的正方形得到①、②两部分,再把①、②两部分拼接成图(2)所示的长方形,根据阴影部分面积不变,你能验证以下哪个结论( )
A.(m﹣n)2=m2﹣2mn+n2 B.(m+n)2=m2+2mn+n2
C.(m﹣n)2=m2+n2 D.m2﹣n2=(m+n)(m﹣n)
7.对于任意整数n,多项式(n+7)2﹣n2都能被( )
A.2整除 B.n整除 C.7整除 D.n+7整除
8.某同学在计算3(4+1)(42+1)时,把3写成4﹣1后,发现可以连续运用两数和乘以这两数差公式计算:3(4+1)(42+1)=(4﹣1)(4+1)(42+1)=(42﹣1)(42+1)=162﹣1=255.请借鉴该同学的经验,计算:=( )
A.2﹣ B.2+ C.1 D.2
9.若一个正整数能表示为两个连续奇数的平方差,则称这个正整数为“好数”.下列正整数中能称为“好数”的是( )
A.205 B.250 C.502 D.520
10.(2+1)(22+1)(24+1)(28+1)(216+1)+1的计算结果的个位数字是( )
A.8 B.6 C.4 D.2
二.填空题
11.已知x+y=5,x﹣y=﹣2,则x2﹣y2= .
12.在边长为a的正方形中挖掉一边长为b的小正方形(a>b),把余下的部分剪成直角梯形后,再拼成一个等腰梯形(如图),通过计算阴影部分的面积,验证了一个等式,这个等式是 .
13.计算2021×2019﹣20202的值为 .
14.若(a+b+1)(a+b﹣1)=15,则a+b的值为 .
15.在括号内填入适当的整式:(2a+b)( )=b2﹣4a2.
16.当x=1时,ax+b+1的值为﹣3,则(a+b+1)(1﹣a﹣b)的值为 .
17.若a2﹣b2=﹣,a+b=﹣,则a﹣b的值为 .
三.解答题
18.计算:(x﹣y﹣3)(x+y﹣3).
19.计算:(3x+2)(3x﹣2)﹣x(5﹣3x).
20.小亮在课余时间写了三个算式:32﹣12=8×1,52﹣32=8×2,72﹣52=8×3,通过认真观察,发现任意两个连续奇数的平方差是8的倍数.
验证:
(1)92﹣72的结果是8的几倍?
(2)设两个连续奇数为2n+1,2n﹣1(其中n为正整数),写出它们的平方差,并说明结果是8的倍数;
延伸:
直接写出两个连续偶数的平方差是几的倍数.
参考答案
一.选择题
1. B.
2. C.
3. B.
4. B.
5. D.
6. D.
7. C.
8. D.
9. D.
10. B.
二.填空题
11.﹣10.
12. a2﹣b2=(a+b)(a﹣b).
13.﹣1.
14.±4.
15. b﹣2a.
16.﹣15.
17. .
三.解答题
18.解:(x﹣y﹣3)(x+y﹣3)
=(x﹣3)2﹣y2
=x2﹣6x+9﹣y2.
19.解:原式=9x2﹣4﹣5x+3x2
=12x2﹣5x﹣4.
20.解:(1)92﹣72=81﹣49=32,32是8的4倍;
(2)设两个连续奇数为2n+1,2n﹣1(其中n为正整数),
则它们的平方差是8的倍数;
(2n+1)2﹣(2n﹣1)2=(2n+1﹣2n+1)(2n+1+2n﹣1)=2×4n=8n,
故两个连续奇数的平方差是8的倍数.
延伸:
82﹣62=64﹣36=28,
两个连续偶数的平方差是4的倍数.
一.选择题
1.(1﹣2x)(1+2x)的计算结果是( )
A.4x2+1 B.1﹣4x2 C.4x2 D.﹣4x2﹣1
2.在下列多项式的乘法中,可以用平方差公式计算的是( )
A.(2x+y)(2y﹣x) B.(x+1)(﹣x﹣1)
C.(3x﹣y)(3x+y) D.(x﹣y)(﹣x+y)
3.下列运算一定正确的是( )
A.3a+3a=6a2 B.(a+b)(a﹣b)=a2﹣b2
C.(a3)4=a7 D.a2?a3=a6
4.已知x,y满足,则x2﹣y2的值为( )
A.8 B.﹣8 C.10 D.﹣10
5.若s﹣t=7,则s2﹣t2﹣14t的值是( )
A.42 B.50 C.56 D.49
6.如图(1),边长为m的正方形剪去边长为n的正方形得到①、②两部分,再把①、②两部分拼接成图(2)所示的长方形,根据阴影部分面积不变,你能验证以下哪个结论( )
A.(m﹣n)2=m2﹣2mn+n2 B.(m+n)2=m2+2mn+n2
C.(m﹣n)2=m2+n2 D.m2﹣n2=(m+n)(m﹣n)
7.对于任意整数n,多项式(n+7)2﹣n2都能被( )
A.2整除 B.n整除 C.7整除 D.n+7整除
8.某同学在计算3(4+1)(42+1)时,把3写成4﹣1后,发现可以连续运用两数和乘以这两数差公式计算:3(4+1)(42+1)=(4﹣1)(4+1)(42+1)=(42﹣1)(42+1)=162﹣1=255.请借鉴该同学的经验,计算:=( )
A.2﹣ B.2+ C.1 D.2
9.若一个正整数能表示为两个连续奇数的平方差,则称这个正整数为“好数”.下列正整数中能称为“好数”的是( )
A.205 B.250 C.502 D.520
10.(2+1)(22+1)(24+1)(28+1)(216+1)+1的计算结果的个位数字是( )
A.8 B.6 C.4 D.2
二.填空题
11.已知x+y=5,x﹣y=﹣2,则x2﹣y2= .
12.在边长为a的正方形中挖掉一边长为b的小正方形(a>b),把余下的部分剪成直角梯形后,再拼成一个等腰梯形(如图),通过计算阴影部分的面积,验证了一个等式,这个等式是 .
13.计算2021×2019﹣20202的值为 .
14.若(a+b+1)(a+b﹣1)=15,则a+b的值为 .
15.在括号内填入适当的整式:(2a+b)( )=b2﹣4a2.
16.当x=1时,ax+b+1的值为﹣3,则(a+b+1)(1﹣a﹣b)的值为 .
17.若a2﹣b2=﹣,a+b=﹣,则a﹣b的值为 .
三.解答题
18.计算:(x﹣y﹣3)(x+y﹣3).
19.计算:(3x+2)(3x﹣2)﹣x(5﹣3x).
20.小亮在课余时间写了三个算式:32﹣12=8×1,52﹣32=8×2,72﹣52=8×3,通过认真观察,发现任意两个连续奇数的平方差是8的倍数.
验证:
(1)92﹣72的结果是8的几倍?
(2)设两个连续奇数为2n+1,2n﹣1(其中n为正整数),写出它们的平方差,并说明结果是8的倍数;
延伸:
直接写出两个连续偶数的平方差是几的倍数.
参考答案
一.选择题
1. B.
2. C.
3. B.
4. B.
5. D.
6. D.
7. C.
8. D.
9. D.
10. B.
二.填空题
11.﹣10.
12. a2﹣b2=(a+b)(a﹣b).
13.﹣1.
14.±4.
15. b﹣2a.
16.﹣15.
17. .
三.解答题
18.解:(x﹣y﹣3)(x+y﹣3)
=(x﹣3)2﹣y2
=x2﹣6x+9﹣y2.
19.解:原式=9x2﹣4﹣5x+3x2
=12x2﹣5x﹣4.
20.解:(1)92﹣72=81﹣49=32,32是8的4倍;
(2)设两个连续奇数为2n+1,2n﹣1(其中n为正整数),
则它们的平方差是8的倍数;
(2n+1)2﹣(2n﹣1)2=(2n+1﹣2n+1)(2n+1+2n﹣1)=2×4n=8n,
故两个连续奇数的平方差是8的倍数.
延伸:
82﹣62=64﹣36=28,
两个连续偶数的平方差是4的倍数.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
