四年级上册数学教案-9.1 植树问题冀教版
文档属性
| 名称 | 四年级上册数学教案-9.1 植树问题冀教版 |  | |
| 格式 | docx | ||
| 文件大小 | 46.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-14 08:37:40 | ||
图片预览



文档简介
《植树问题》教学设计
教学目标
1.了解段数的含义,建构解答植树问题的一般方法模型,能解答类似的简单实际问题。
2.结合具体事例,经历分析问题、解决问题、总结解答植树问题一般方法的过程,建立起解答植树问题的思想方法模型。
3.在用植树问题的思路和方法解答其他问题的过程中,获得成功的体验,感受数学与生活的密切联系。
重点、难点
重点:理解段数的含义,能求出段数并根据两端植树的情况,利用模型思想求出植树的棵数。
难点:运用植树问题的模型思想方法解决简单实际问题。
教学准备
教师准备: 多媒体教学课件。
学生准备: 铅笔、橡皮、直尺。
教学过程
(一)新课导入
师:图中人物是谁?
生:光头强。
师:他在干嘛呢?
生:砍树。
师:砍完树的光头强,遇到的一个难题(出示PPT题目:一根木头总长20米,每段5米,可以锯成几段?)你能帮帮他吗?
生:能。
师:请同学们在学案的第一部分,列式计算,答语可以省略不写,开始。
(学生动手解答,教师巡视,选一名学生把答案写在黑板上20÷5=4(段))。
师:这名同学的答案可以吗?
生:可以。
师:那么这个算式中的20是指什么?
生:总长。(板书:总长)
师:5指什么?
生:段长。(板书:段长)
师:那求出的4指的是什么?
生:把木头锯成了4段。
师:我们就把4叫做段数。有几段,段数就是几。(板书:段数)
师:通过这样一个简单的数学问题,其实我们总结出来了一个数量关系,同学们一起来说。(板书:总长÷段长=段数)
师:很准确。光头强需要锯几次?
生:3次。
师:课件演示。次数要比段数少一。
(二)探究新知
1.提出问题,设计方案
师:虽然,刚才我们帮了光头强,但是光头强乱砍乱伐,破坏森林的行为对吗?
生:不对。
师:我们要向熊大、熊二学习,保护森林,今天就让我们一起跟着熊大、熊二去种树。这是狗熊岭小学明年的种树计划。(课件显示)学校计划在总长20米的教学楼前种一排玉兰树,每隔5米种一棵。
师:这里的20米,指的是什么?
生:总长。
师:每隔5米种一棵,5米就是?
生:段长。
师:按照这样种,路被分成了几段呢??
生:4段。
师:好,现在把小路分成了4段,在这种情况下去种树,应该怎么种?可以种几棵呢?请同学们在学案上的第二部分画一画,看看小树苗可以种在哪里呢?计时1分钟,开始。(教师巡视,抽选学生把方案展示在黑板上)
2.讨论交流,展示方案?
师:好,我们来交流一下,这是1号同学的方案,这位同学种了几棵树?
生:5棵。
师:(手指着图)4段路5棵树。2号同学种了几棵树?
生:3棵。
师:(手指着图)4段路3棵树。3号同学种了几棵树?
生:4棵。
师:(手指着图)4段路4棵树。我刚才巡视了一圈,基本上都是这三种情况吧。(如果学生们找不全方案,教师可以参与补全种树方案。)
生:是。
3.探究发现,总结规律
师:这里出现了3种种树的方案。每种方案中棵数和段数之间有什么规律呢?同学们想不想探究一下?
生:想。
师:好,在探究之前我们先来看一下探究任务(PPT出示探究任务),1.给每种情况起个名字;2.每种情况下种树“棵数”和路的“段数”之间有什么数量关系?接下来请同学们以小组为单位进行探究,并把探究结果写在学案的第三部分,计时3分钟,开始(教师巡视)。
师:好,哪位同学来跟大家汇报第一种情况时,棵数和段数之间的关系?
生:棵数=段数+1(教师在板书:棵数=段数+1)
师:同意吗?
生:同意。
师:好,请坐。
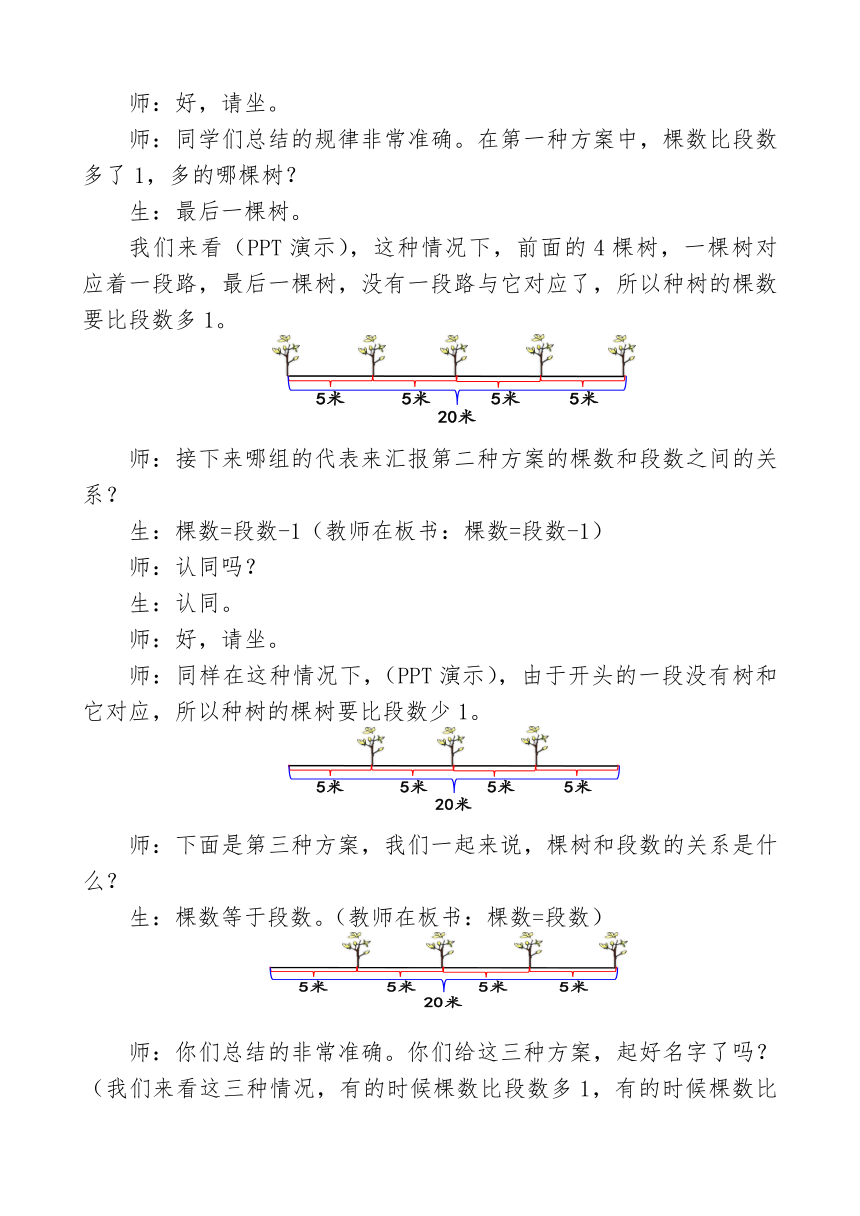
师:同学们总结的规律非常准确。在第一种方案中,棵数比段数多了1,多的哪棵树?
生:最后一棵树。
我们来看(PPT演示),这种情况下,前面的4棵树,一棵树对应着一段路,最后一棵树,没有一段路与它对应了,所以种树的棵数要比段数多1。
5米
5米
20米
5米
5米
师:接下来哪组的代表来汇报第二种方案的棵数和段数之间的关系?
生:棵数=段数-1(教师在板书:棵数=段数-1)
师:认同吗?
生:认同。
师:好,请坐。
师:同样在这种情况下,(PPT演示),由于开头的一段没有树和它对应,所以种树的棵树要比段数少1。
5米
5米
20米
5米
5米
师:下面是第三种方案,我们一起来说,棵树和段数的关系是什么?
生:棵数等于段数。(教师在板书:棵数=段数)
5米
5米
20米
5米
5米
师:你们总结的非常准确。你们给这三种方案,起好名字了吗?(我们来看这三种情况,有的时候棵数比段数多1,有的时候棵数比段数少1,有的时候棵数等于段数。同学们仔细观察,是种在哪个位置上的树影响了结果呢?)
生:起好了。第一种是两头都种。
师:我真佩服你们的火眼金睛。(手指黑板上第一种情况)第一种情况是两头都种时,棵树等于段数加一。(板书:两端都种)所以,第二种情况,应该叫做什么呢?
生:两端都不种。(板书:两端都不种)
师:那第三种情况呢?
生:一端种一端不种。(板书:一端种一端不种)
师:你们的本领真大,起的名字真有水平。那一端种一端不种时,除了这种还有没有其他情况?
生:头种尾不种,和尾种头不种。
师:看来这个名字下包括了两种情况。(在黑板上贴上另一种情况)
?4.举一反三,融会贯通
师:你们真了不起,一个植树的问题,就引发了你们这么多的思考。你们知道这个规律还在哪儿吗?伸出来你们的右手,几根手指?(5根)几个缝隙?(4个)。5根手指相当于我们刚才种的5棵树,4个缝隙就是刚才的4段。请同学们听我口令,用你的小手上来种树。我们规定大拇指表示头,小拇指表示尾。尾种,头不种。种了几棵树?(4棵)头种,尾不种。几棵树?(4棵)头尾都不种,几棵树?(3棵)头尾都种,几棵树?(5棵)
师:真好,看来植树问题就长在我们的手上。来,把它一圈,变成了一个封闭的圆(PPT出示)。在这个圆上,我们用一个绿点来表示一棵树,这是我们的5棵树。这个圆分成了几段呢?(5段)一个段配一棵树。棵数就等于段数。
(三)巩固新知?
1.师:手就在我们身上,有了这个模型,是不是就不怕忘记棵数和段数的关系了?好,接下来,我们就来动手解决一下这个实际问题。(课件显示)?
同学们在长是90米的小路同一侧植树,每隔6米种一棵,两端各种一棵,一共需要多少棵树苗????
师:认真审题。题目中的种树方法是哪种情况呢?
生:两端都种。
师:能解决吗?在你的学案上列式计算。
2分钟。
交流汇报。
(90米是总长,6米是段长,90÷6=15求出来的是段数,两端都种时,棵数比段数多1,所以一共需要15+1=16棵。)
师:各小组组长,快速浏览一遍本组完成情况。哪组有问题?
生:……
师:同学们真棒,什么也难不倒你们。如果这条路的两侧都植树,怎样计算??
学生自己独立完成。
2.师:用我们这节课学习的知识,只能解决种树问题吗?还能不能种别的?
师:“种”电线杆、摆盆花、插红旗、上楼梯等一段一段的问题,我们统称为“植树问题”。比如这个摆盆花的问题,你能解决吗?(PPT出示)认真审题,在你的学案上尝试着列式计算。
学校在16米长的教室前面均匀地摆了9盆鲜花,两端都摆。每两盆鲜花之间相隔几米?
2分钟。
汇报交流。…师:各小组组长,快速浏览一遍本组完成情况。哪组有问题?
生:……
(问题是两盆鲜花之间相隔几米,也就是在问段长是多少。要求段长,需要知道总长和段数。总长知道了吗?是多少?段数知道了吗?能求出来吗?两端都摆盆花时,棵数比段数多1,也就是段数比棵数少1,所以段数就是9-1=8段,段长就是16÷8=2米。)
3.师:同学们,你们认识这位运动员吗?他叫刘翔,是一位跨栏运动员,在雅典奥运会上他以12秒91的成绩追平了世界纪录,获得了奥运冠军。那你知道刘翔从起点到终点一共跑了多少米吗?(PPT出示)
起点至第一栏的距离为13.72米;中间共有10个栏,栏间距离为9.14米;最后一栏至终点的距离是14.02米;你们知道他从起点到终点跑了多少米吗?
师:小明同学和小红同学学完植树问题后,也计算了一下刘翔一共跑了多少米,但是算出的结果却不一样,谁的计算结果正确呢?小明错在了哪里?希望同学们在以后的计算中也要像小红一样,考虑清楚段数和棵数之间的关系。
(四)课堂小结
师:今天我们大家一起探究了植树问题,体会了植树问题与生活间的密切联系。现在和同桌说一说,通过本课的学习,你有哪些收获?还有哪些困惑?
(五)布置作业
1. 某小区要在52米长的小路两边种树,每隔4米种一棵,两头都不种。一共需要准备多少棵树苗?
2.丽丽家到学校之间有7根电线杆,每两根电线杆之间的距离都是30米。丽丽家到学校有多远?
3.(1)小强家住在5楼,小强从一楼到二楼12个台阶,每两层之间的台阶数相同。小强回家一共要上多少个台阶?
(2)小丽和小强住在同一个单元,小丽每天从楼上下来要走36个台阶。小丽家住在几楼?
板书设计
植树问题
20÷5=4(段)
总长÷段长=段数
两端都种????? 棵数=段数+1
两端不种?? 棵数=段数-1 只种一端 棵数=段数
教学目标
1.了解段数的含义,建构解答植树问题的一般方法模型,能解答类似的简单实际问题。
2.结合具体事例,经历分析问题、解决问题、总结解答植树问题一般方法的过程,建立起解答植树问题的思想方法模型。
3.在用植树问题的思路和方法解答其他问题的过程中,获得成功的体验,感受数学与生活的密切联系。
重点、难点
重点:理解段数的含义,能求出段数并根据两端植树的情况,利用模型思想求出植树的棵数。
难点:运用植树问题的模型思想方法解决简单实际问题。
教学准备
教师准备: 多媒体教学课件。
学生准备: 铅笔、橡皮、直尺。
教学过程
(一)新课导入
师:图中人物是谁?
生:光头强。
师:他在干嘛呢?
生:砍树。
师:砍完树的光头强,遇到的一个难题(出示PPT题目:一根木头总长20米,每段5米,可以锯成几段?)你能帮帮他吗?
生:能。
师:请同学们在学案的第一部分,列式计算,答语可以省略不写,开始。
(学生动手解答,教师巡视,选一名学生把答案写在黑板上20÷5=4(段))。
师:这名同学的答案可以吗?
生:可以。
师:那么这个算式中的20是指什么?
生:总长。(板书:总长)
师:5指什么?
生:段长。(板书:段长)
师:那求出的4指的是什么?
生:把木头锯成了4段。
师:我们就把4叫做段数。有几段,段数就是几。(板书:段数)
师:通过这样一个简单的数学问题,其实我们总结出来了一个数量关系,同学们一起来说。(板书:总长÷段长=段数)
师:很准确。光头强需要锯几次?
生:3次。
师:课件演示。次数要比段数少一。
(二)探究新知
1.提出问题,设计方案
师:虽然,刚才我们帮了光头强,但是光头强乱砍乱伐,破坏森林的行为对吗?
生:不对。
师:我们要向熊大、熊二学习,保护森林,今天就让我们一起跟着熊大、熊二去种树。这是狗熊岭小学明年的种树计划。(课件显示)学校计划在总长20米的教学楼前种一排玉兰树,每隔5米种一棵。
师:这里的20米,指的是什么?
生:总长。
师:每隔5米种一棵,5米就是?
生:段长。
师:按照这样种,路被分成了几段呢??
生:4段。
师:好,现在把小路分成了4段,在这种情况下去种树,应该怎么种?可以种几棵呢?请同学们在学案上的第二部分画一画,看看小树苗可以种在哪里呢?计时1分钟,开始。(教师巡视,抽选学生把方案展示在黑板上)
2.讨论交流,展示方案?
师:好,我们来交流一下,这是1号同学的方案,这位同学种了几棵树?
生:5棵。
师:(手指着图)4段路5棵树。2号同学种了几棵树?
生:3棵。
师:(手指着图)4段路3棵树。3号同学种了几棵树?
生:4棵。
师:(手指着图)4段路4棵树。我刚才巡视了一圈,基本上都是这三种情况吧。(如果学生们找不全方案,教师可以参与补全种树方案。)
生:是。
3.探究发现,总结规律
师:这里出现了3种种树的方案。每种方案中棵数和段数之间有什么规律呢?同学们想不想探究一下?
生:想。
师:好,在探究之前我们先来看一下探究任务(PPT出示探究任务),1.给每种情况起个名字;2.每种情况下种树“棵数”和路的“段数”之间有什么数量关系?接下来请同学们以小组为单位进行探究,并把探究结果写在学案的第三部分,计时3分钟,开始(教师巡视)。
师:好,哪位同学来跟大家汇报第一种情况时,棵数和段数之间的关系?
生:棵数=段数+1(教师在板书:棵数=段数+1)
师:同意吗?
生:同意。
师:好,请坐。
师:同学们总结的规律非常准确。在第一种方案中,棵数比段数多了1,多的哪棵树?
生:最后一棵树。
我们来看(PPT演示),这种情况下,前面的4棵树,一棵树对应着一段路,最后一棵树,没有一段路与它对应了,所以种树的棵数要比段数多1。
5米
5米
20米
5米
5米
师:接下来哪组的代表来汇报第二种方案的棵数和段数之间的关系?
生:棵数=段数-1(教师在板书:棵数=段数-1)
师:认同吗?
生:认同。
师:好,请坐。
师:同样在这种情况下,(PPT演示),由于开头的一段没有树和它对应,所以种树的棵树要比段数少1。
5米
5米
20米
5米
5米
师:下面是第三种方案,我们一起来说,棵树和段数的关系是什么?
生:棵数等于段数。(教师在板书:棵数=段数)
5米
5米
20米
5米
5米
师:你们总结的非常准确。你们给这三种方案,起好名字了吗?(我们来看这三种情况,有的时候棵数比段数多1,有的时候棵数比段数少1,有的时候棵数等于段数。同学们仔细观察,是种在哪个位置上的树影响了结果呢?)
生:起好了。第一种是两头都种。
师:我真佩服你们的火眼金睛。(手指黑板上第一种情况)第一种情况是两头都种时,棵树等于段数加一。(板书:两端都种)所以,第二种情况,应该叫做什么呢?
生:两端都不种。(板书:两端都不种)
师:那第三种情况呢?
生:一端种一端不种。(板书:一端种一端不种)
师:你们的本领真大,起的名字真有水平。那一端种一端不种时,除了这种还有没有其他情况?
生:头种尾不种,和尾种头不种。
师:看来这个名字下包括了两种情况。(在黑板上贴上另一种情况)
?4.举一反三,融会贯通
师:你们真了不起,一个植树的问题,就引发了你们这么多的思考。你们知道这个规律还在哪儿吗?伸出来你们的右手,几根手指?(5根)几个缝隙?(4个)。5根手指相当于我们刚才种的5棵树,4个缝隙就是刚才的4段。请同学们听我口令,用你的小手上来种树。我们规定大拇指表示头,小拇指表示尾。尾种,头不种。种了几棵树?(4棵)头种,尾不种。几棵树?(4棵)头尾都不种,几棵树?(3棵)头尾都种,几棵树?(5棵)
师:真好,看来植树问题就长在我们的手上。来,把它一圈,变成了一个封闭的圆(PPT出示)。在这个圆上,我们用一个绿点来表示一棵树,这是我们的5棵树。这个圆分成了几段呢?(5段)一个段配一棵树。棵数就等于段数。
(三)巩固新知?
1.师:手就在我们身上,有了这个模型,是不是就不怕忘记棵数和段数的关系了?好,接下来,我们就来动手解决一下这个实际问题。(课件显示)?
同学们在长是90米的小路同一侧植树,每隔6米种一棵,两端各种一棵,一共需要多少棵树苗????
师:认真审题。题目中的种树方法是哪种情况呢?
生:两端都种。
师:能解决吗?在你的学案上列式计算。
2分钟。
交流汇报。
(90米是总长,6米是段长,90÷6=15求出来的是段数,两端都种时,棵数比段数多1,所以一共需要15+1=16棵。)
师:各小组组长,快速浏览一遍本组完成情况。哪组有问题?
生:……
师:同学们真棒,什么也难不倒你们。如果这条路的两侧都植树,怎样计算??
学生自己独立完成。
2.师:用我们这节课学习的知识,只能解决种树问题吗?还能不能种别的?
师:“种”电线杆、摆盆花、插红旗、上楼梯等一段一段的问题,我们统称为“植树问题”。比如这个摆盆花的问题,你能解决吗?(PPT出示)认真审题,在你的学案上尝试着列式计算。
学校在16米长的教室前面均匀地摆了9盆鲜花,两端都摆。每两盆鲜花之间相隔几米?
2分钟。
汇报交流。…师:各小组组长,快速浏览一遍本组完成情况。哪组有问题?
生:……
(问题是两盆鲜花之间相隔几米,也就是在问段长是多少。要求段长,需要知道总长和段数。总长知道了吗?是多少?段数知道了吗?能求出来吗?两端都摆盆花时,棵数比段数多1,也就是段数比棵数少1,所以段数就是9-1=8段,段长就是16÷8=2米。)
3.师:同学们,你们认识这位运动员吗?他叫刘翔,是一位跨栏运动员,在雅典奥运会上他以12秒91的成绩追平了世界纪录,获得了奥运冠军。那你知道刘翔从起点到终点一共跑了多少米吗?(PPT出示)
起点至第一栏的距离为13.72米;中间共有10个栏,栏间距离为9.14米;最后一栏至终点的距离是14.02米;你们知道他从起点到终点跑了多少米吗?
师:小明同学和小红同学学完植树问题后,也计算了一下刘翔一共跑了多少米,但是算出的结果却不一样,谁的计算结果正确呢?小明错在了哪里?希望同学们在以后的计算中也要像小红一样,考虑清楚段数和棵数之间的关系。
(四)课堂小结
师:今天我们大家一起探究了植树问题,体会了植树问题与生活间的密切联系。现在和同桌说一说,通过本课的学习,你有哪些收获?还有哪些困惑?
(五)布置作业
1. 某小区要在52米长的小路两边种树,每隔4米种一棵,两头都不种。一共需要准备多少棵树苗?
2.丽丽家到学校之间有7根电线杆,每两根电线杆之间的距离都是30米。丽丽家到学校有多远?
3.(1)小强家住在5楼,小强从一楼到二楼12个台阶,每两层之间的台阶数相同。小强回家一共要上多少个台阶?
(2)小丽和小强住在同一个单元,小丽每天从楼上下来要走36个台阶。小丽家住在几楼?
板书设计
植树问题
20÷5=4(段)
总长÷段长=段数
两端都种????? 棵数=段数+1
两端不种?? 棵数=段数-1 只种一端 棵数=段数
