沪教版(上海)数学七年级第二学期-15.2 直角坐标平面内点的运动(1) 教案
文档属性
| 名称 | 沪教版(上海)数学七年级第二学期-15.2 直角坐标平面内点的运动(1) 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 87.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-13 00:00:00 | ||
图片预览

文档简介
课题
15.2直角坐标平面内点的运动(1)
课型
新授课(√)
复习课(
)
讲评课(
)
习题课(
)
教学目标
通过类比数轴上两点的距离公式,探索直角坐标平面内平行于坐标轴的直线上两点的距离公式。
体会类比的数学思想方法和从特殊到一般的研究问题的方法;
3、会根据点的坐标求平行于坐标轴的直线上的两点的距离,并解决简单的问题
教学重点
直角坐标平面内平行于坐标轴的直线上两点的距离公式及其应用.
教学难点
直角坐标平面中不规则几何图形的面积的计算.
教学媒体
PPT素材的选择、制作
课前学生准备
1、明确学习重点难点、学习目标。2、尝试自己完成练习。
教
学
流
程
学习内容
教
师
活
动
学
生
活
动
设
计
意
图
一、探索直角坐标平面内平行于坐标轴的直线上两点的距离公式
适时小结:
二、应用
三、
课堂练习:
四、课堂小结
五、布置作业:
1、直角坐标平面内平行于x轴的直线上两点的距离公式
问1:数轴上两点的距离公式是什么?
(PPT展示数轴)
举例说明。
如图,点A与点B的距离是多少?
问2:当数轴作为平面直角坐标系的横轴时,点A与点B的距离是多少?以上的公式是否适用?
师生共同归纳,在直角坐标平面内,x轴上任意两点A(,0)、B(,0)间的距离公式。
问3:若一条直线平行于x轴,这条直线上的点的坐标有何特点?
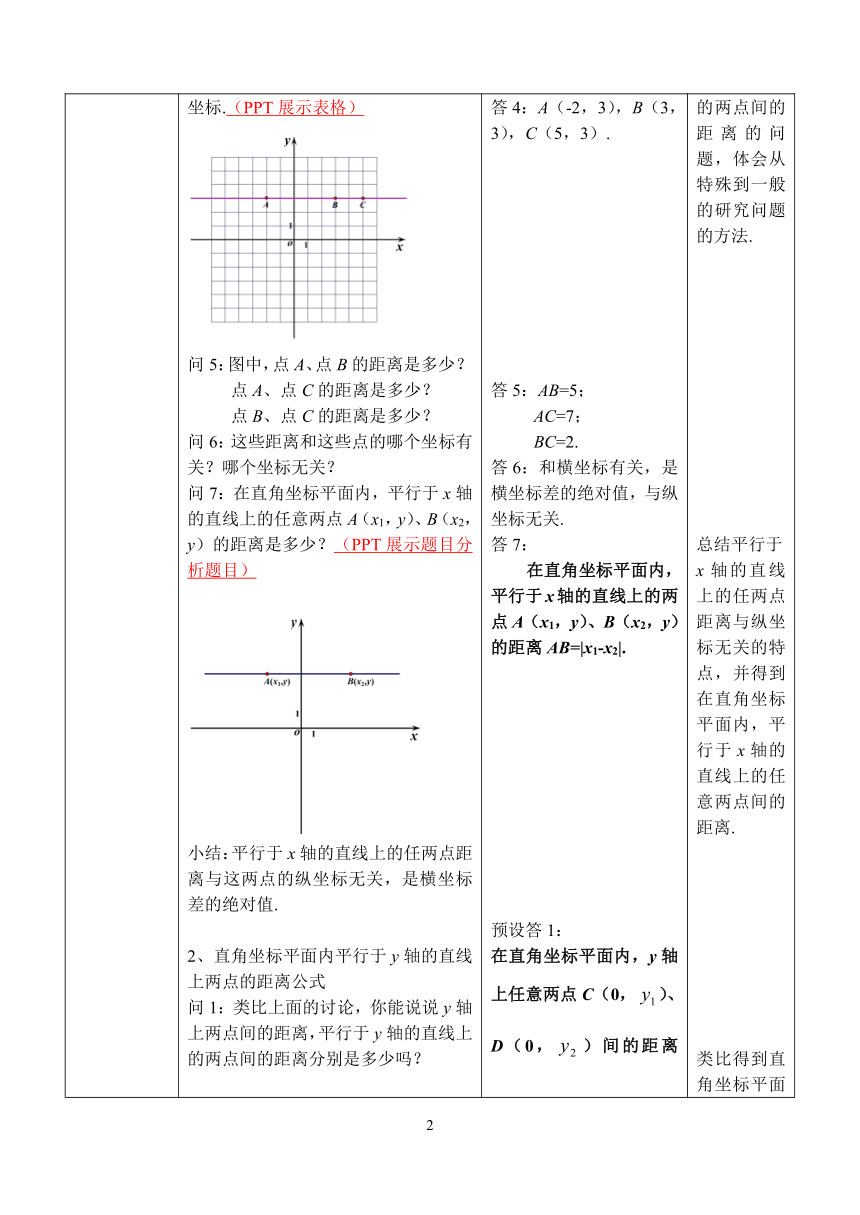
问4:如图,说出点A、点B、点C的坐标.(PPT展示表格)
问5:图中,点A、点B的距离是多少?
点A、点C的距离是多少?
点B、点C的距离是多少?
问6:这些距离和这些点的哪个坐标有关?哪个坐标无关?
问7:在直角坐标平面内,平行于x轴的直线上的任意两点A(x1,y)、B(x2,y)的距离是多少?(PPT展示题目分析题目)
小结:平行于x轴的直线上的任两点距离与这两点的纵坐标无关,是横坐标差的绝对值.
2、直角坐标平面内平行于y轴的直线上两点的距离公式
问1:类比上面的讨论,你能说说y轴上两点间的距离,平行于y轴的直线上的两点间的距离分别是多少吗?
问2:平行于y轴的直线上的任两点距离与这两点的哪个坐标无关?
在直角坐标平面内:
平行于x轴的直线(或x轴)上任意两点的距离与这两点的纵坐标无关,是横坐标差的绝对值;
平行于y轴的直线(或y轴)上任意两点的距离与这两点的横坐标无关,是纵坐标差的绝对值.
②公式适用的前提:在同一坐标轴上的两点,或同一条平行于坐标轴的直线上的两点.
掌握直角坐标平面内平行于坐标轴的直线上的两点的距离公式可用于几何图形的有关计算,看下面例题.
例题1
如图,在梯形ABCD中,AD//BC,写出点A、B、C、D的坐标,并求图中梯形ABCD的面积.(PPT展示题目分析题目)
问1:点A、B、C、D的坐标分别是什么?
问2:梯形的面积如何求?
问3:梯形的上底、下底、高分别是什么,如何求?
根据学生回答,教师板书解题过程:
解:画梯形的高AE,(PPT展示题目规范的格式)
则E(2,-3);
AD=|2-4|=2;
BC=|-4-5|=9;
AE=|4-(-3)|=7.
梯形ABCD的面积
问4:在直线BC上描出点F,使E、F两点的距离为2个单位,直接写出出图形ABFD的面积.
课本P131,1、2、3
今天主要学习了什么?
教师补充:
③类比的思想方法;从特殊到一般的研究问题的方法.
练习册,习题15.2(1)
答1:在数轴上,如果点A、点B所对应的数分别为a、b,那么A、B两点的距离AB=|a-b|.
点A与点B的距离AB=|-2-3|=5.
答2:点A与点B的距离仍是5.
以上的公式适用.
在直角坐标平面内,x轴上任意两点A(,0)、B(,0)间的距离AB=||.
答3:平行于x轴的直线上的点的纵坐标相同.
答4:A(-2,3),B(3,3),C(5,3).
答5:AB=5;
AC=7;
BC=2.
答6:和横坐标有关,是横坐标差的绝对值,与纵坐标无关.
答7:
在直角坐标平面内,平行于x轴的直线上的两点A(x1,y)、B(x2,y)的距离AB=|x1-x2|.
预设答1:
在直角坐标平面内,y轴上任意两点C(0,)、D(0,)间的距离CD=||;
在直角坐标平面内,平行于y轴的直线上的两点E(x,)、F(x,)的距离EF=||
答2:平行于y轴的直线上的任两点距离与这两点的横坐标无关,是纵坐标差的绝对值.
答1:A(2,4),B(-4,-3),C(5,-3),D(4,4)
答2:
梯形面积=
(上底+下底)高
答3:
上底为AD,由于AD//x轴,A(2,4),D(4,4),所以,AD=|2-4|=2;
下底为BC,由于BC//x轴,B(-4,-3),C(5,-3),所以,BC=|-4-5|=9;
过点A作AEBC,垂足为点E,则AE为梯形的高,且AE//y轴,E(2,-3),所以AE=|4-(-3)|=7.
答:此题需要分类讨论,先求出F(0,-3)或(4,-3),图形ABFD的面积是21或35.
学生独立完成练习,集体纠错讲评
预设:
①在直角坐标平面内,平行于x轴的直线(或x轴)上任意两点的距离是||;平行于y轴的直线(或y轴)上任意两点的距离是||.
②直角坐标平面内图形的面积和周长一般求解过程是:先求点的坐标,再求线段长度,最后,代入公式求解.
复习数轴上两点的距离公式,及在x轴上的点的坐标的特点,为后面的学习作铺垫.
在x轴上的两点的距离实质就是数轴上两点距离.
进一步探索平行于坐标轴的直线上的两点间的距离的问题,体会从特殊到一般的研究问题的方法.
总结平行于x轴的直线上的任两点距离与纵坐标无关的特点,并得到在直角坐标平面内,平行于x轴的直线上的任意两点间的距离.
类比得到直角坐标平面内平行于x轴的直线上两点的距离.
平行于坐标轴的直线上两点的距离公式的简单运用.
注意练习第2题需分类讨论,不要遗漏.
教学后记
PPT演示坐标系来描述物体的位置,能结合具体情境,灵活运用多种形式确定物体的我位置,这也是为本节学习图形变化后各点坐标变化,由于本节课的内容涉及到图形,为了节约时间,提前用PPT准备好图形,方便学生观看和理解图形,由于是PPT原因设计时考虑的不全面,PPT
的字太小了,后面的学生会看不到清楚,所PPT课件的字体大小还是需要改正。
教学设计:
在本节课中,学生能够按照PPT的要求,理解课堂制定的导入,积极小组合作,得到本节课的内容,PPT
的演示,学生等到直角坐标系的关键的公式和概念,通过PPT的演示帮助学生只管的了解了本节课内容
立足于非常实际的背景材料,使学生在相对轻松,有趣的活动中理解坐标思想及其由来,比较系统地学习平面直角坐标系的有关内容,进一步发展学生的合情推理能力和丰富的情感、态度。
建立适当的坐标系来描述物体的位置,能结合具体情境,灵活运用多种形式确定物体的我位置,这也是为本节学习图形变化后各点坐标变化带来了知识的可能,但缺乏数形结合意识,所以应加以引导点拔和启发。恰当地运用教学手段,本节需要大量的坐标纸等材料,事前的准备是必须的,同时建议有条件的地区使用PPT进行动态演示,以报教学效果。
5
15.2直角坐标平面内点的运动(1)
课型
新授课(√)
复习课(
)
讲评课(
)
习题课(
)
教学目标
通过类比数轴上两点的距离公式,探索直角坐标平面内平行于坐标轴的直线上两点的距离公式。
体会类比的数学思想方法和从特殊到一般的研究问题的方法;
3、会根据点的坐标求平行于坐标轴的直线上的两点的距离,并解决简单的问题
教学重点
直角坐标平面内平行于坐标轴的直线上两点的距离公式及其应用.
教学难点
直角坐标平面中不规则几何图形的面积的计算.
教学媒体
PPT素材的选择、制作
课前学生准备
1、明确学习重点难点、学习目标。2、尝试自己完成练习。
教
学
流
程
学习内容
教
师
活
动
学
生
活
动
设
计
意
图
一、探索直角坐标平面内平行于坐标轴的直线上两点的距离公式
适时小结:
二、应用
三、
课堂练习:
四、课堂小结
五、布置作业:
1、直角坐标平面内平行于x轴的直线上两点的距离公式
问1:数轴上两点的距离公式是什么?
(PPT展示数轴)
举例说明。
如图,点A与点B的距离是多少?
问2:当数轴作为平面直角坐标系的横轴时,点A与点B的距离是多少?以上的公式是否适用?
师生共同归纳,在直角坐标平面内,x轴上任意两点A(,0)、B(,0)间的距离公式。
问3:若一条直线平行于x轴,这条直线上的点的坐标有何特点?
问4:如图,说出点A、点B、点C的坐标.(PPT展示表格)
问5:图中,点A、点B的距离是多少?
点A、点C的距离是多少?
点B、点C的距离是多少?
问6:这些距离和这些点的哪个坐标有关?哪个坐标无关?
问7:在直角坐标平面内,平行于x轴的直线上的任意两点A(x1,y)、B(x2,y)的距离是多少?(PPT展示题目分析题目)
小结:平行于x轴的直线上的任两点距离与这两点的纵坐标无关,是横坐标差的绝对值.
2、直角坐标平面内平行于y轴的直线上两点的距离公式
问1:类比上面的讨论,你能说说y轴上两点间的距离,平行于y轴的直线上的两点间的距离分别是多少吗?
问2:平行于y轴的直线上的任两点距离与这两点的哪个坐标无关?
在直角坐标平面内:
平行于x轴的直线(或x轴)上任意两点的距离与这两点的纵坐标无关,是横坐标差的绝对值;
平行于y轴的直线(或y轴)上任意两点的距离与这两点的横坐标无关,是纵坐标差的绝对值.
②公式适用的前提:在同一坐标轴上的两点,或同一条平行于坐标轴的直线上的两点.
掌握直角坐标平面内平行于坐标轴的直线上的两点的距离公式可用于几何图形的有关计算,看下面例题.
例题1
如图,在梯形ABCD中,AD//BC,写出点A、B、C、D的坐标,并求图中梯形ABCD的面积.(PPT展示题目分析题目)
问1:点A、B、C、D的坐标分别是什么?
问2:梯形的面积如何求?
问3:梯形的上底、下底、高分别是什么,如何求?
根据学生回答,教师板书解题过程:
解:画梯形的高AE,(PPT展示题目规范的格式)
则E(2,-3);
AD=|2-4|=2;
BC=|-4-5|=9;
AE=|4-(-3)|=7.
梯形ABCD的面积
问4:在直线BC上描出点F,使E、F两点的距离为2个单位,直接写出出图形ABFD的面积.
课本P131,1、2、3
今天主要学习了什么?
教师补充:
③类比的思想方法;从特殊到一般的研究问题的方法.
练习册,习题15.2(1)
答1:在数轴上,如果点A、点B所对应的数分别为a、b,那么A、B两点的距离AB=|a-b|.
点A与点B的距离AB=|-2-3|=5.
答2:点A与点B的距离仍是5.
以上的公式适用.
在直角坐标平面内,x轴上任意两点A(,0)、B(,0)间的距离AB=||.
答3:平行于x轴的直线上的点的纵坐标相同.
答4:A(-2,3),B(3,3),C(5,3).
答5:AB=5;
AC=7;
BC=2.
答6:和横坐标有关,是横坐标差的绝对值,与纵坐标无关.
答7:
在直角坐标平面内,平行于x轴的直线上的两点A(x1,y)、B(x2,y)的距离AB=|x1-x2|.
预设答1:
在直角坐标平面内,y轴上任意两点C(0,)、D(0,)间的距离CD=||;
在直角坐标平面内,平行于y轴的直线上的两点E(x,)、F(x,)的距离EF=||
答2:平行于y轴的直线上的任两点距离与这两点的横坐标无关,是纵坐标差的绝对值.
答1:A(2,4),B(-4,-3),C(5,-3),D(4,4)
答2:
梯形面积=
(上底+下底)高
答3:
上底为AD,由于AD//x轴,A(2,4),D(4,4),所以,AD=|2-4|=2;
下底为BC,由于BC//x轴,B(-4,-3),C(5,-3),所以,BC=|-4-5|=9;
过点A作AEBC,垂足为点E,则AE为梯形的高,且AE//y轴,E(2,-3),所以AE=|4-(-3)|=7.
答:此题需要分类讨论,先求出F(0,-3)或(4,-3),图形ABFD的面积是21或35.
学生独立完成练习,集体纠错讲评
预设:
①在直角坐标平面内,平行于x轴的直线(或x轴)上任意两点的距离是||;平行于y轴的直线(或y轴)上任意两点的距离是||.
②直角坐标平面内图形的面积和周长一般求解过程是:先求点的坐标,再求线段长度,最后,代入公式求解.
复习数轴上两点的距离公式,及在x轴上的点的坐标的特点,为后面的学习作铺垫.
在x轴上的两点的距离实质就是数轴上两点距离.
进一步探索平行于坐标轴的直线上的两点间的距离的问题,体会从特殊到一般的研究问题的方法.
总结平行于x轴的直线上的任两点距离与纵坐标无关的特点,并得到在直角坐标平面内,平行于x轴的直线上的任意两点间的距离.
类比得到直角坐标平面内平行于x轴的直线上两点的距离.
平行于坐标轴的直线上两点的距离公式的简单运用.
注意练习第2题需分类讨论,不要遗漏.
教学后记
PPT演示坐标系来描述物体的位置,能结合具体情境,灵活运用多种形式确定物体的我位置,这也是为本节学习图形变化后各点坐标变化,由于本节课的内容涉及到图形,为了节约时间,提前用PPT准备好图形,方便学生观看和理解图形,由于是PPT原因设计时考虑的不全面,PPT
的字太小了,后面的学生会看不到清楚,所PPT课件的字体大小还是需要改正。
教学设计:
在本节课中,学生能够按照PPT的要求,理解课堂制定的导入,积极小组合作,得到本节课的内容,PPT
的演示,学生等到直角坐标系的关键的公式和概念,通过PPT的演示帮助学生只管的了解了本节课内容
立足于非常实际的背景材料,使学生在相对轻松,有趣的活动中理解坐标思想及其由来,比较系统地学习平面直角坐标系的有关内容,进一步发展学生的合情推理能力和丰富的情感、态度。
建立适当的坐标系来描述物体的位置,能结合具体情境,灵活运用多种形式确定物体的我位置,这也是为本节学习图形变化后各点坐标变化带来了知识的可能,但缺乏数形结合意识,所以应加以引导点拔和启发。恰当地运用教学手段,本节需要大量的坐标纸等材料,事前的准备是必须的,同时建议有条件的地区使用PPT进行动态演示,以报教学效果。
5
