2020-2021学年人教版八年级下册数学 17.1勾股定理 同步测试 (Word版 含解析)
文档属性
| 名称 | 2020-2021学年人教版八年级下册数学 17.1勾股定理 同步测试 (Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 199.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-13 21:07:43 | ||
图片预览



文档简介
17.1勾股定理 同步测试
一.选择题
1.已知直角三角形的两条直角边的长分别为1和2,则斜边的长为( )
A. B. C.3 D.5
2.在△ABC中,AB=AC=5,BC=6,M是BC的中点,MN⊥AC于点N,则MN=( )
A. B. C.6 D.11
3.如图,在Rt△ABC中,分别以三角形的三条边为边向外作正方形,面积分别记为S1,S2,S3.若S1=9,S2=16,则S3的值为( )
A.7 B.10 C.20 D.25
4.2002年8月在北京召开的国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是13,小正方形的面积是1,直角三角形的较长直角边为a,较短直角边为b,则(a+b)2的值为( )
A.25 B.19 C.13 D.169
5.直角三角形两直角边长为a,b,斜边上高为h,则下列各式总能成立的是( )
A.ab=h2 B.a2+b2=2h2
C.+= D.+=
6.小明学了在数轴上表示无理数的方法后,进行了练习:首先画数轴,原点为O,在数轴上找到表示数2的点A,然后过点A作AB⊥OA,使AB=1;再以O为圆心,OB的长为半径作弧,交数轴正半轴于点P,那么点P表示的数是( )
A.2.2 B. C. D.
7.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,BE平分∠ABC,CD⊥AB于D,BE与CD相交于F,则CF的长是( )
A.1 B. C. D.2
8.如图,在△ABC中,∠C=90°,点D在边BC上,AD=BD,DE平分∠ADB交AB于点E.若AC=12,BC=16,则AE的长为( )
A.6 B.8 C.10 D.12
9.如图,是我国古代著名的“赵爽弦图”的示意图,此图是由四个全等的直角三角形拼接而成,其中AE=10,BE=24,则EF的长是( )
A.14 B.13 C.14 D.14
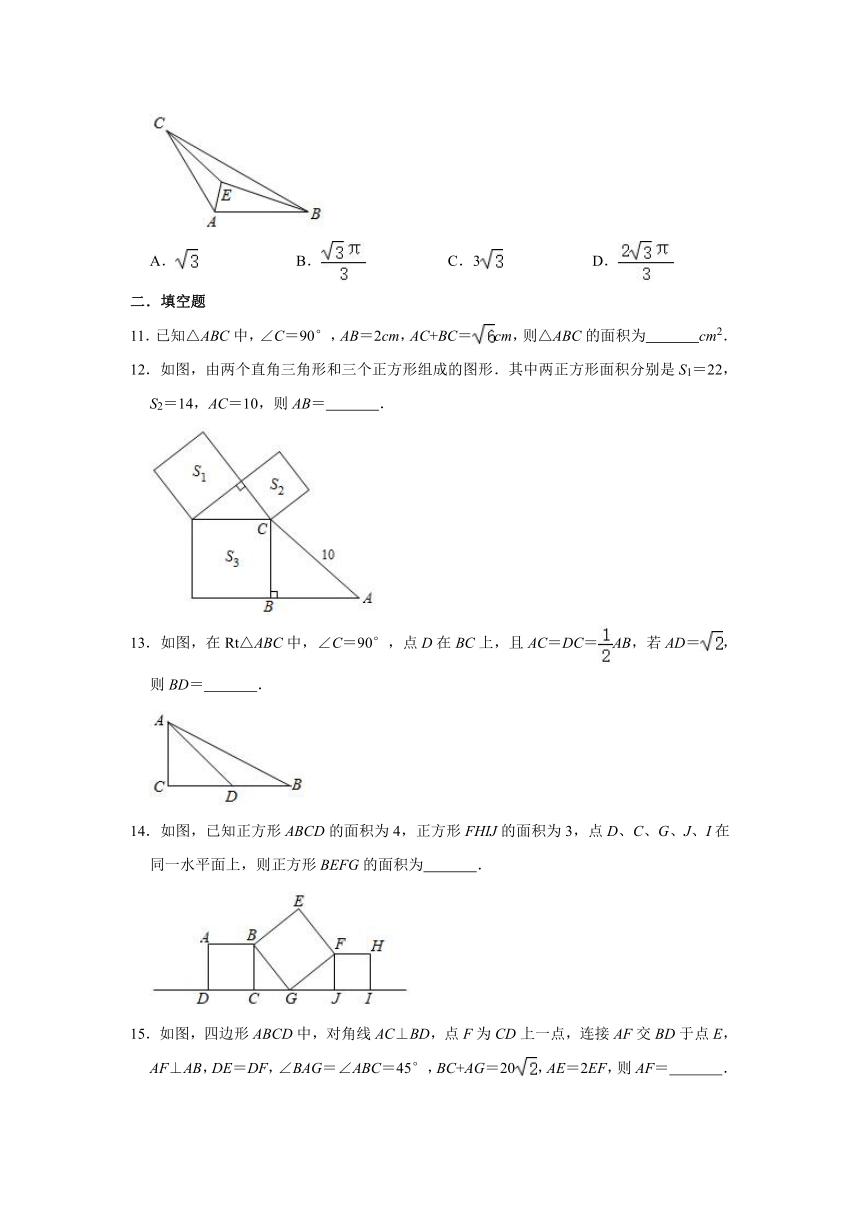
10.如图,在△ABC中,∠CAB=120°,AB=AC=3,点E是三角形ABC内部一点,且满足BE2﹣CE2=3AE2,则点E在运动过程中所形成的图形的长为( )
A. B. C.3 D.
二.填空题
11.已知△ABC中,∠C=90°,AB=2cm,AC+BC=cm,则△ABC的面积为 cm2.
12.如图,由两个直角三角形和三个正方形组成的图形.其中两正方形面积分别是S1=22,S2=14,AC=10,则AB= .
13.如图,在Rt△ABC中,∠C=90°,点D在BC上,且AC=DC=AB,若AD=,则BD= .
14.如图,已知正方形ABCD的面积为4,正方形FHIJ的面积为3,点D、C、G、J、I在同一水平面上,则正方形BEFG的面积为 .
15.如图,四边形ABCD中,对角线AC⊥BD,点F为CD上一点,连接AF交BD于点E,AF⊥AB,DE=DF,∠BAG=∠ABC=45°,BC+AG=20,AE=2EF,则AF= .
三.解答题
16.如图,在△ABC中,∠C=90°,若CD=1.5,BD=2.5.
(1)∠2=∠B,求AC的长.
(2)∠1=∠2,求AC的长.
17.如图,在△ABC中,延长AC至点D,使CD=AC,过点D作DE∥AB交BC的延长线于点E,延长DE至点F,使EF=DE.连接AF.
(1)求证:DE=AB;
(2)求证:AF∥BE;
(3)当AC=BC时,连接AE,求证:AE2+DE2=AD2.
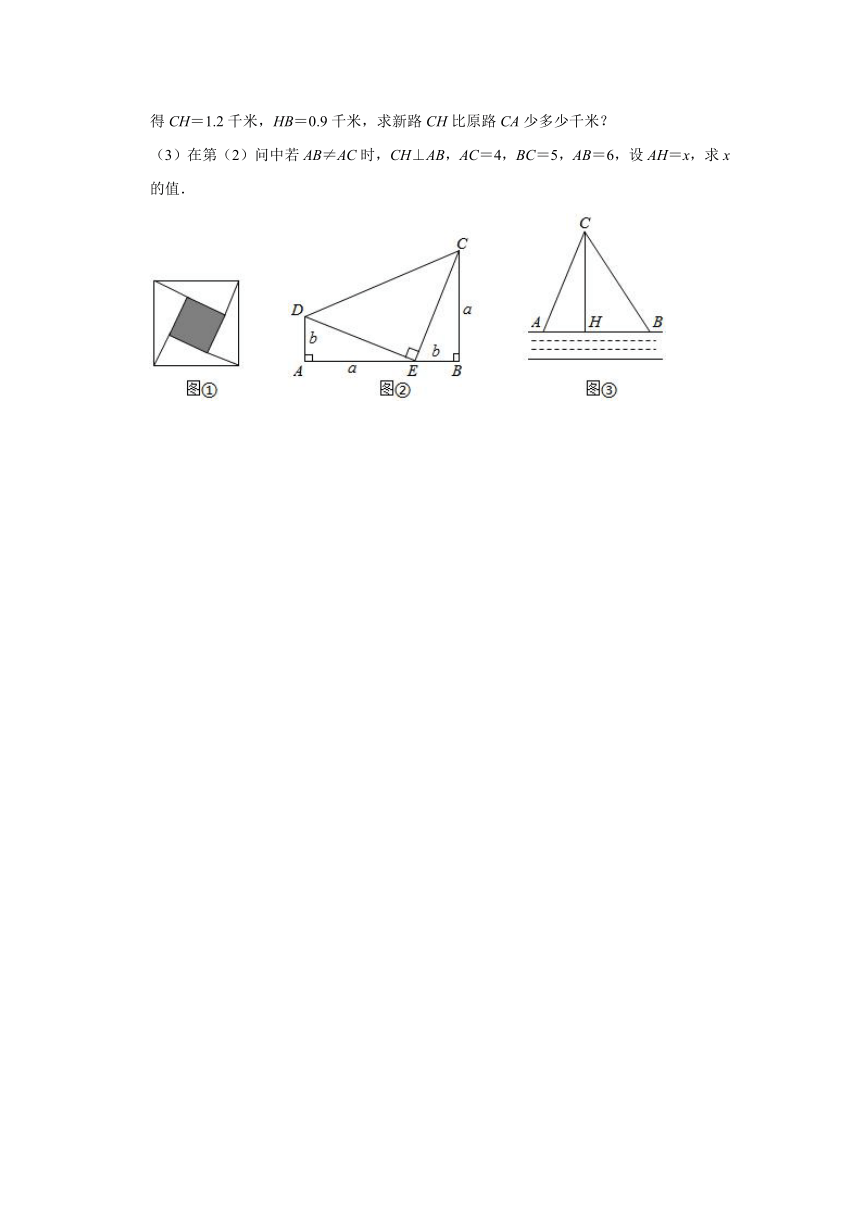
18.著名的赵爽弦图(如图①,其中四个直角三角形较大的直角边长都为a,较小的直角边长都为b,斜边长都为c),大正方形的面积可以表示为c),也可以表示为4×ab+(a﹣b)2,由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则a2+b2=c2.
(1)图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理.
(2)如图③,在一条东西走向河流的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点H(A、H、B在同一条直线上),并新修一条路CH,且CH⊥AB.测得CH=1.2千米,HB=0.9千米,求新路CH比原路CA少多少千米?
(3)在第(2)问中若AB≠AC时,CH⊥AB,AC=4,BC=5,AB=6,设AH=x,求x的值.
参考答案
一.选择题
1.解:∵直角三角形的两条直角边的长分别为1和2,
∴斜边的长为:.
故选:B.
2.解:连接AM,
∵AB=AC,点M为BC中点,
∴AM⊥CM(三线合一),BM=CM,
∵AB=AC=5,BC=6,
∴BM=CM=3,
在Rt△ABM中,AB=5,BM=3,
∴根据勾股定理得:AM===4,
又S△AMC=MN?AC=AM?MC,
∴MN==.
故选:A.
3.解:在Rt△ABC中,AC2+AB2=BC2,
由正方形面积公式得S1=AB2,S2=AC2,S3=BC2,
∵S1=9,S2=16,
∴S3=S1+S2=9+16=25.
故选:D.
4.解:由条件可得:,
解之得:.
所以(a+b)2=25,
故选:A.
5.解:根据直角三角形的面积可以导出:斜边c=.
再结合勾股定理:a2+b2=c2.
进行等量代换,得a2+b2=.
两边同除以a2b2,得+=.
故选:D.
6.解:在Rt△OAB中,OA=2,AB=1,
∴OB===.
∴以点O为圆心,OB为半径与正半轴交点P表示的数为.
故选:B.
7.解:过点E作EG⊥AB于点G,如图:
∵CD⊥AB于D,
∴EG∥CD,
∴∠GEB=∠EFC,
∵在Rt△ABC中,∠ACB=90°,
∴EC⊥CB,
又∵BE平分∠ABC,EG⊥AB,
∴EG=EC.
在Rt△ABC中,∠ACB=90°,AC=3,BC=4,
∴AB=5.
在Rt△EBC和Rt△EBG中,
,
∴Rt△EBC≌Rt△EBG(HL),
∠CEB=∠GEB,BG=BC=4,
∴∠CEB=∠EFC,AG=AB﹣BG=5﹣4=1,
∴CF=CE.
设CF=EG=EC=x,则AE=3﹣x,
在Rt△AEG中,由勾股定理得:
(3﹣x)2=x2+12,
解得x=
∴CF的长是.
故选:B.
8.解:如图,在△ABC中,∠C=90°,AC=12,BC=16,
由勾股定理知:AB===20.
∵AD=BD,DE平分∠ADB交AB于点E.
∴AE=BE=AB=10.
故选:C.
9.解:∵AE=10,BE=24,即24和10为两条直角边长时,
小正方形的边长=24﹣10=14,
∴EF==14.
故选:D.
10.解:将△AEC绕点A顺时针旋转120°,使得AC与AB重合,得到△AFB,连接EF,过点A作AM⊥EF,过点O作ON⊥AC,如图:
由旋转可知:AE=AF,∠EAF=120°,BF=CE,
∴∠AEF=∠AFE=30°,
在Rt△AEM中,EM=AE;在Rt△AFM中,MF=AF;
∴EF=EM+FM=AE,
∴EF2=3AE2,
∵BE2﹣CE2=3AE2,
∴BE2﹣BF2=EF2,
∴∠EFB=90°,
∴∠AFB=120°,
∴∠GOA=60°,
在Rt△OAN中,=sin60°=,
∴=,
∴OA=.
∴点E在运动过程中所形成的图形的长为=.
故选:B.
二.填空题
11.解:∵△ABC中,∠C=90°,
∴AB2=AC2+BC2,
即4=AC2+BC2,
∵AC+BC=(cm),
∴(AC+BC)2=AC2+2AC?BC+BC2=4+2AC?BC=6,
∴AC?BC=1,
∴,
故答案为:.
12.解:∵S1=22,S2=14,
∴S3=S1+S2=22+14=36,
∴BC==6,
∵AC=10,
∴AB===8,
故答案为:8.
13.解:∵AD=,∠C=90°,AC=DC,
∴AC=CD=1,
∵AC=DC=AB,
∴AB=2,
∴BC==,
∴BD=﹣1,
故答案为:﹣1.
14.解:∵四边形ABCD、四边形FHIJ和四边形BEFG都是正方形,
∴∠BCG=∠BGF=∠GJF=90°,BG=GF,
∴∠CBG+∠BGC=90°,∠JGF+∠BGC=90°,
∴∠CBG=∠JGF,
在△BCG和△GJF中,
,
∴△BCG≌△GJF(AAS),
∴BC=GJ,
∵正方形ABCD的面积为4,正方形FHIJ的面积为3,
∴BC2=4,FJ2=3,
∴GJ2=4,
在Rt△GJF中,由勾股定理得:
FG2=GJ2+FJ2=4+3=7,
∴正方形BEFG的面积为7.
故答案为:7.
15.解:延长AF、BC,交于点H,如图:
∵AF⊥AB,∠ABC=45°,
∴∠BAH=90°,∠AHB=90°﹣∠ABC=45°,
∴△ABH为等腰直角三角形,
∴AH=AB,
∵∠BAH=90°,∠BAG=45°,∠AHB=45°,
∴∠GAE=∠BAG=∠AHB=45°,
∵AC⊥BD,
∴∠ABG+∠BAC=90°,
∵∠BAC+∠HAC=∠BAH=90°,
∴∠ABG=∠HAC,
在△ABG和△HAC中,
,
∴△ABG≌△HAC(ASA),
∴AG=HC,
BH=BC+CH=BC+AG=20,
在等腰直角三角形△ABH中,AH=AB,∠BAH=90°,由勾股定理得:
AB2+AH2=BH2,
∴AB=AH=20,
∵AE=2EF,
∴设EF=x,则AE=2x,
∵DE=DF,
∴∠DEF=∠DFE,
∴∠AEG=∠HFC,
∵∠AHB=∠GAE=45°,
∴∠AGE=135°﹣∠HFC=∠FCH,
在△AGE和△HCF中,
,
∴△AGE≌△HCF(AAS),
∴FH=AE=2x,
∴AH=AE+EF+FH=5x=20,
解得:x=4,
∴AF=AE+EF=3x=12,
故答案为:12.
三.解答题
16.解:(1)∵∠2=∠B,
∴AD=BD=2.5,
∵∠C=90°,CD=1.5,
∴AC=,
(2)过点D作DE⊥AB于点E,
∵∠1=∠2,∠C=90°,DE⊥AB,
∴CD=DE=1.5,AC=AE,
在Rt△DEB中,BE=,
在Rt△ACB中,AC2=AB2﹣BC2,
即AC2=(AE+EB)2﹣(CD+DB)2,
可得:AC2=(AC+2)2﹣(1.5+2.5)2,
解得:AC=3.
17.证明:(1)∵DE∥AB,
∴∠ABC=∠DEC,
在△ABC和△DEC中,
,
∴△ABC≌△DEC(AAS),
∴DE=AB;
(2)∵DC=AC,DE=EF,
∴CE是△DAF的中位线,
∴AF∥BE;
(3)∵△ABC≌△DEC,
∴BC=CE,
∵AC=BC,
∴AC=BC=CE,
∴△BAE是直角三角形,
∴AB2+AE2=BE2,
∵AB=DE,AD=2AC=2BC=BE,
∴AE2+DE2=AD2.
18.解:(1)梯形ABCD的面积为(a+b)(a+b)=a2+ab+b2,
也可以表示为ab+ab+c2,
∴ab+ab+c2=a2+ab+b2,
即a2+b2=c2;
(2)∵CA=x,
∴AH=x﹣0.9,
在Rt△ACH中,CA2=CH2+AH2,
即x2=1.22+(x﹣0.9)2,
解得x=1.25,
即CA=1.25,
CA﹣CH=1.25﹣1.2=0.05(千米),
答:新路CH比原路CA少0.05千米;
(3)设AH=x,则BH=6﹣x,
在Rt△ACH中,CH2=CA2﹣AH2,
在Rt△BCH中,CH2=CB2﹣BH2,
∴CA2﹣AH2=CB2﹣BH2,
即42﹣x2=52﹣(6﹣x)2,
解得:x=.
一.选择题
1.已知直角三角形的两条直角边的长分别为1和2,则斜边的长为( )
A. B. C.3 D.5
2.在△ABC中,AB=AC=5,BC=6,M是BC的中点,MN⊥AC于点N,则MN=( )
A. B. C.6 D.11
3.如图,在Rt△ABC中,分别以三角形的三条边为边向外作正方形,面积分别记为S1,S2,S3.若S1=9,S2=16,则S3的值为( )
A.7 B.10 C.20 D.25
4.2002年8月在北京召开的国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是13,小正方形的面积是1,直角三角形的较长直角边为a,较短直角边为b,则(a+b)2的值为( )
A.25 B.19 C.13 D.169
5.直角三角形两直角边长为a,b,斜边上高为h,则下列各式总能成立的是( )
A.ab=h2 B.a2+b2=2h2
C.+= D.+=
6.小明学了在数轴上表示无理数的方法后,进行了练习:首先画数轴,原点为O,在数轴上找到表示数2的点A,然后过点A作AB⊥OA,使AB=1;再以O为圆心,OB的长为半径作弧,交数轴正半轴于点P,那么点P表示的数是( )
A.2.2 B. C. D.
7.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,BE平分∠ABC,CD⊥AB于D,BE与CD相交于F,则CF的长是( )
A.1 B. C. D.2
8.如图,在△ABC中,∠C=90°,点D在边BC上,AD=BD,DE平分∠ADB交AB于点E.若AC=12,BC=16,则AE的长为( )
A.6 B.8 C.10 D.12
9.如图,是我国古代著名的“赵爽弦图”的示意图,此图是由四个全等的直角三角形拼接而成,其中AE=10,BE=24,则EF的长是( )
A.14 B.13 C.14 D.14
10.如图,在△ABC中,∠CAB=120°,AB=AC=3,点E是三角形ABC内部一点,且满足BE2﹣CE2=3AE2,则点E在运动过程中所形成的图形的长为( )
A. B. C.3 D.
二.填空题
11.已知△ABC中,∠C=90°,AB=2cm,AC+BC=cm,则△ABC的面积为 cm2.
12.如图,由两个直角三角形和三个正方形组成的图形.其中两正方形面积分别是S1=22,S2=14,AC=10,则AB= .
13.如图,在Rt△ABC中,∠C=90°,点D在BC上,且AC=DC=AB,若AD=,则BD= .
14.如图,已知正方形ABCD的面积为4,正方形FHIJ的面积为3,点D、C、G、J、I在同一水平面上,则正方形BEFG的面积为 .
15.如图,四边形ABCD中,对角线AC⊥BD,点F为CD上一点,连接AF交BD于点E,AF⊥AB,DE=DF,∠BAG=∠ABC=45°,BC+AG=20,AE=2EF,则AF= .
三.解答题
16.如图,在△ABC中,∠C=90°,若CD=1.5,BD=2.5.
(1)∠2=∠B,求AC的长.
(2)∠1=∠2,求AC的长.
17.如图,在△ABC中,延长AC至点D,使CD=AC,过点D作DE∥AB交BC的延长线于点E,延长DE至点F,使EF=DE.连接AF.
(1)求证:DE=AB;
(2)求证:AF∥BE;
(3)当AC=BC时,连接AE,求证:AE2+DE2=AD2.
18.著名的赵爽弦图(如图①,其中四个直角三角形较大的直角边长都为a,较小的直角边长都为b,斜边长都为c),大正方形的面积可以表示为c),也可以表示为4×ab+(a﹣b)2,由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则a2+b2=c2.
(1)图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理.
(2)如图③,在一条东西走向河流的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点H(A、H、B在同一条直线上),并新修一条路CH,且CH⊥AB.测得CH=1.2千米,HB=0.9千米,求新路CH比原路CA少多少千米?
(3)在第(2)问中若AB≠AC时,CH⊥AB,AC=4,BC=5,AB=6,设AH=x,求x的值.
参考答案
一.选择题
1.解:∵直角三角形的两条直角边的长分别为1和2,
∴斜边的长为:.
故选:B.
2.解:连接AM,
∵AB=AC,点M为BC中点,
∴AM⊥CM(三线合一),BM=CM,
∵AB=AC=5,BC=6,
∴BM=CM=3,
在Rt△ABM中,AB=5,BM=3,
∴根据勾股定理得:AM===4,
又S△AMC=MN?AC=AM?MC,
∴MN==.
故选:A.
3.解:在Rt△ABC中,AC2+AB2=BC2,
由正方形面积公式得S1=AB2,S2=AC2,S3=BC2,
∵S1=9,S2=16,
∴S3=S1+S2=9+16=25.
故选:D.
4.解:由条件可得:,
解之得:.
所以(a+b)2=25,
故选:A.
5.解:根据直角三角形的面积可以导出:斜边c=.
再结合勾股定理:a2+b2=c2.
进行等量代换,得a2+b2=.
两边同除以a2b2,得+=.
故选:D.
6.解:在Rt△OAB中,OA=2,AB=1,
∴OB===.
∴以点O为圆心,OB为半径与正半轴交点P表示的数为.
故选:B.
7.解:过点E作EG⊥AB于点G,如图:
∵CD⊥AB于D,
∴EG∥CD,
∴∠GEB=∠EFC,
∵在Rt△ABC中,∠ACB=90°,
∴EC⊥CB,
又∵BE平分∠ABC,EG⊥AB,
∴EG=EC.
在Rt△ABC中,∠ACB=90°,AC=3,BC=4,
∴AB=5.
在Rt△EBC和Rt△EBG中,
,
∴Rt△EBC≌Rt△EBG(HL),
∠CEB=∠GEB,BG=BC=4,
∴∠CEB=∠EFC,AG=AB﹣BG=5﹣4=1,
∴CF=CE.
设CF=EG=EC=x,则AE=3﹣x,
在Rt△AEG中,由勾股定理得:
(3﹣x)2=x2+12,
解得x=
∴CF的长是.
故选:B.
8.解:如图,在△ABC中,∠C=90°,AC=12,BC=16,
由勾股定理知:AB===20.
∵AD=BD,DE平分∠ADB交AB于点E.
∴AE=BE=AB=10.
故选:C.
9.解:∵AE=10,BE=24,即24和10为两条直角边长时,
小正方形的边长=24﹣10=14,
∴EF==14.
故选:D.
10.解:将△AEC绕点A顺时针旋转120°,使得AC与AB重合,得到△AFB,连接EF,过点A作AM⊥EF,过点O作ON⊥AC,如图:
由旋转可知:AE=AF,∠EAF=120°,BF=CE,
∴∠AEF=∠AFE=30°,
在Rt△AEM中,EM=AE;在Rt△AFM中,MF=AF;
∴EF=EM+FM=AE,
∴EF2=3AE2,
∵BE2﹣CE2=3AE2,
∴BE2﹣BF2=EF2,
∴∠EFB=90°,
∴∠AFB=120°,
∴∠GOA=60°,
在Rt△OAN中,=sin60°=,
∴=,
∴OA=.
∴点E在运动过程中所形成的图形的长为=.
故选:B.
二.填空题
11.解:∵△ABC中,∠C=90°,
∴AB2=AC2+BC2,
即4=AC2+BC2,
∵AC+BC=(cm),
∴(AC+BC)2=AC2+2AC?BC+BC2=4+2AC?BC=6,
∴AC?BC=1,
∴,
故答案为:.
12.解:∵S1=22,S2=14,
∴S3=S1+S2=22+14=36,
∴BC==6,
∵AC=10,
∴AB===8,
故答案为:8.
13.解:∵AD=,∠C=90°,AC=DC,
∴AC=CD=1,
∵AC=DC=AB,
∴AB=2,
∴BC==,
∴BD=﹣1,
故答案为:﹣1.
14.解:∵四边形ABCD、四边形FHIJ和四边形BEFG都是正方形,
∴∠BCG=∠BGF=∠GJF=90°,BG=GF,
∴∠CBG+∠BGC=90°,∠JGF+∠BGC=90°,
∴∠CBG=∠JGF,
在△BCG和△GJF中,
,
∴△BCG≌△GJF(AAS),
∴BC=GJ,
∵正方形ABCD的面积为4,正方形FHIJ的面积为3,
∴BC2=4,FJ2=3,
∴GJ2=4,
在Rt△GJF中,由勾股定理得:
FG2=GJ2+FJ2=4+3=7,
∴正方形BEFG的面积为7.
故答案为:7.
15.解:延长AF、BC,交于点H,如图:
∵AF⊥AB,∠ABC=45°,
∴∠BAH=90°,∠AHB=90°﹣∠ABC=45°,
∴△ABH为等腰直角三角形,
∴AH=AB,
∵∠BAH=90°,∠BAG=45°,∠AHB=45°,
∴∠GAE=∠BAG=∠AHB=45°,
∵AC⊥BD,
∴∠ABG+∠BAC=90°,
∵∠BAC+∠HAC=∠BAH=90°,
∴∠ABG=∠HAC,
在△ABG和△HAC中,
,
∴△ABG≌△HAC(ASA),
∴AG=HC,
BH=BC+CH=BC+AG=20,
在等腰直角三角形△ABH中,AH=AB,∠BAH=90°,由勾股定理得:
AB2+AH2=BH2,
∴AB=AH=20,
∵AE=2EF,
∴设EF=x,则AE=2x,
∵DE=DF,
∴∠DEF=∠DFE,
∴∠AEG=∠HFC,
∵∠AHB=∠GAE=45°,
∴∠AGE=135°﹣∠HFC=∠FCH,
在△AGE和△HCF中,
,
∴△AGE≌△HCF(AAS),
∴FH=AE=2x,
∴AH=AE+EF+FH=5x=20,
解得:x=4,
∴AF=AE+EF=3x=12,
故答案为:12.
三.解答题
16.解:(1)∵∠2=∠B,
∴AD=BD=2.5,
∵∠C=90°,CD=1.5,
∴AC=,
(2)过点D作DE⊥AB于点E,
∵∠1=∠2,∠C=90°,DE⊥AB,
∴CD=DE=1.5,AC=AE,
在Rt△DEB中,BE=,
在Rt△ACB中,AC2=AB2﹣BC2,
即AC2=(AE+EB)2﹣(CD+DB)2,
可得:AC2=(AC+2)2﹣(1.5+2.5)2,
解得:AC=3.
17.证明:(1)∵DE∥AB,
∴∠ABC=∠DEC,
在△ABC和△DEC中,
,
∴△ABC≌△DEC(AAS),
∴DE=AB;
(2)∵DC=AC,DE=EF,
∴CE是△DAF的中位线,
∴AF∥BE;
(3)∵△ABC≌△DEC,
∴BC=CE,
∵AC=BC,
∴AC=BC=CE,
∴△BAE是直角三角形,
∴AB2+AE2=BE2,
∵AB=DE,AD=2AC=2BC=BE,
∴AE2+DE2=AD2.
18.解:(1)梯形ABCD的面积为(a+b)(a+b)=a2+ab+b2,
也可以表示为ab+ab+c2,
∴ab+ab+c2=a2+ab+b2,
即a2+b2=c2;
(2)∵CA=x,
∴AH=x﹣0.9,
在Rt△ACH中,CA2=CH2+AH2,
即x2=1.22+(x﹣0.9)2,
解得x=1.25,
即CA=1.25,
CA﹣CH=1.25﹣1.2=0.05(千米),
答:新路CH比原路CA少0.05千米;
(3)设AH=x,则BH=6﹣x,
在Rt△ACH中,CH2=CA2﹣AH2,
在Rt△BCH中,CH2=CB2﹣BH2,
∴CA2﹣AH2=CB2﹣BH2,
即42﹣x2=52﹣(6﹣x)2,
解得:x=.
