2020--2021学年人教版八年级数学下册19.1.2:函数的图像课件(第三课时 28张)
文档属性
| 名称 | 2020--2021学年人教版八年级数学下册19.1.2:函数的图像课件(第三课时 28张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 514.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-13 00:00:00 | ||
图片预览





文档简介
19.1.2 函数的图象
第3课时 函数的表示
一. 像 1 . S=60t; 2. y=10x ; 3. L=10+0.5m
函数关系是用数学式子给出的 (叫解析法)
二. 前面像体检心电图函数关系是用图象给出的
(叫图象法)
三 .前面刘翔的竞赛成绩函数关系是用表格给出的
(叫列表法)
函数的三种表示法
对函数来说,图象法是非常直观的一种表示方法,它能形象的表示函数随自变量的变化而变化的趋势,所以是十分常见且重要的。
图象上每个点的横纵坐标有何实际意义?
你还能从图中看出哪些信息?
下图测温仪记录的图象,它反映了北京的春季某天气温T如何随时间t的变化而变化。
4
14
24
t/小时
8
T/℃
0
-3
你能看出与上图有哪些不同?
一般地,对于一个函数,如果把自变量
与函数的每对对应值分别作为点的横坐标和
纵坐标,那么坐标平面内由这些点组成的图形就是这个函数的图象。
函数的图象的意义:
归纳
八年级 数学
第十四章 一次函数
15
25
37
55
80
0
1.1
2
y/千米
x/分
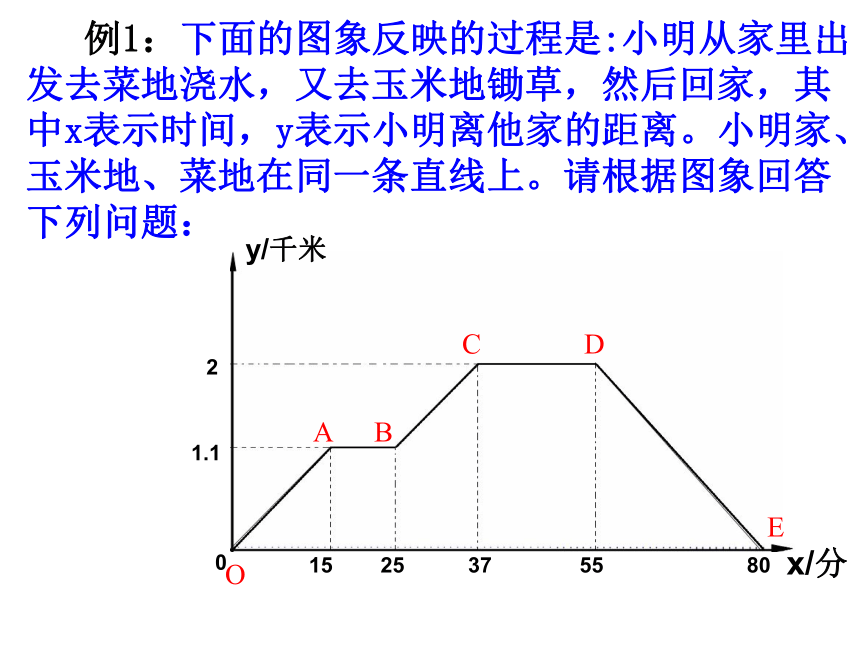
例1:下面的图象反映的过程是:小明从家里出发去菜地浇水,又去玉米地锄草,然后回家,其中x表示时间,y表示小明离他家的距离。小明家、玉米地、菜地在同一条直线上。请根据图象回答下列问题:
A
D
B
C
E
O
八年级 数学
第十四章 一次函数
15
25
37
55
80
0
1.1
2
y/千米
x/分
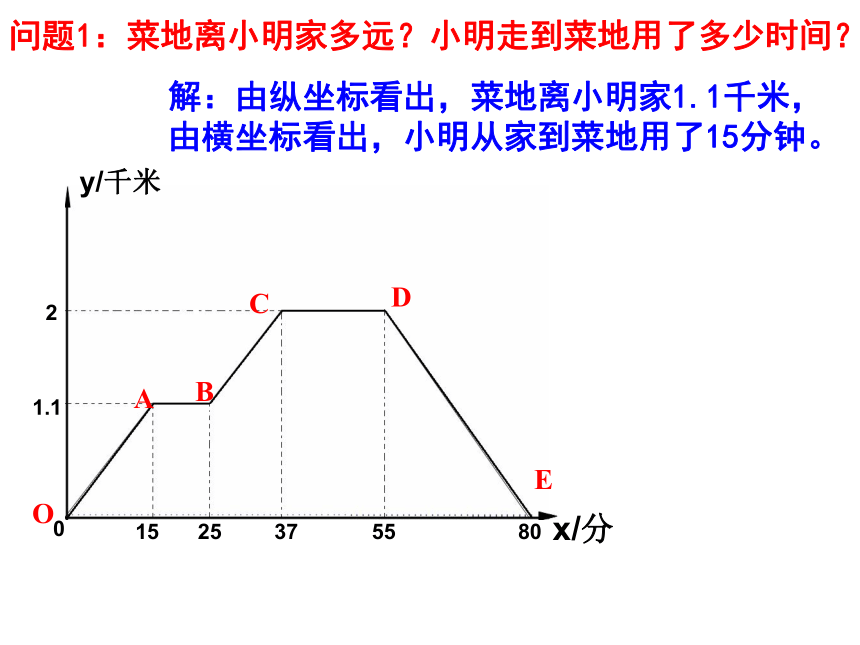
问题1:菜地离小明家多远?小明走到菜地用了多少时间?
解:由纵坐标看出,菜地离小明家1.1千米,由横坐标看出,小明从家到菜地用了15分钟。
A
O
B
C
D
E
八年级 数学
第十四章 一次函数
15
25
37
55
80
0
1.1
2
y/千米
x/分
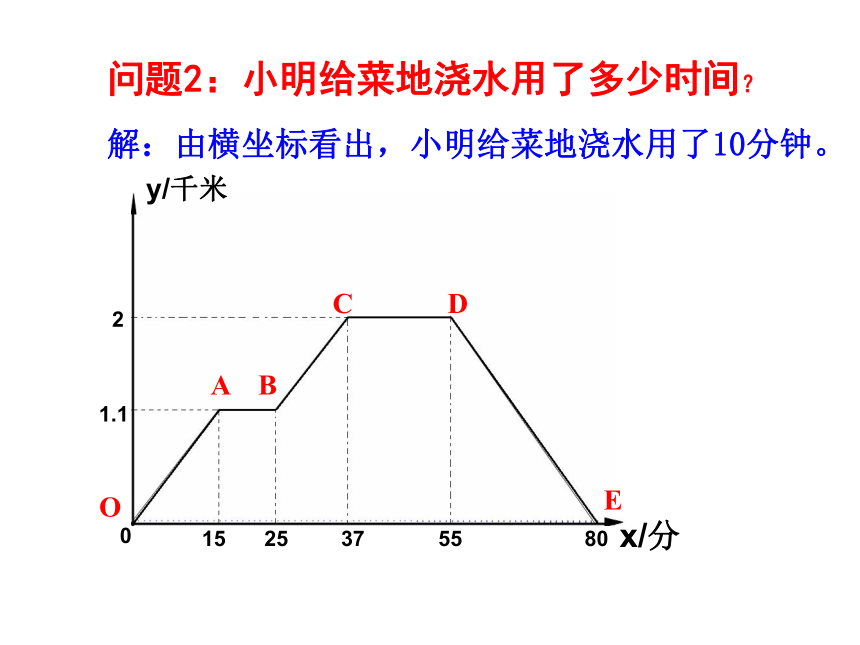
问题2:小明给菜地浇水用了多少时间?
解:由横坐标看出,小明给菜地浇水用了10分钟。
A
B
O
C
D
E
第十四章 一次函数
15
25
37
55
80
0
1.1
2
y/千米
x/分
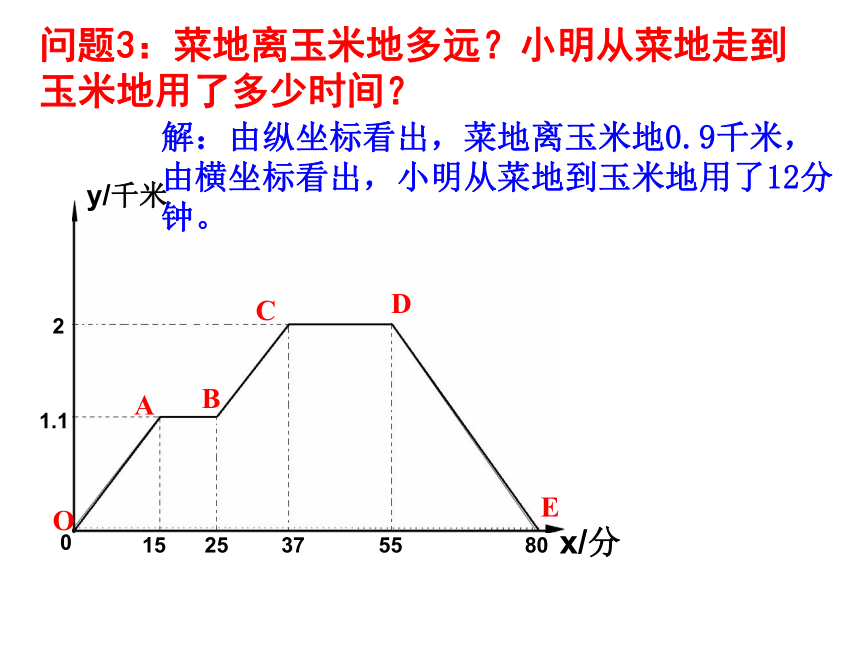
问题3:菜地离玉米地多远?小明从菜地走到玉米地用了多少时间?
C
B
解:由纵坐标看出,菜地离玉米地0.9千米,由横坐标看出,小明从菜地到玉米地用了12分钟。
O
A
D
E
八年级 数学
第十四章 一次函数
15
25
37
55
80
0
1.1
2
y/千米
x/分
问题4:小明给玉米地锄草用了多少时间?
解:由横坐标看出,小明给玉米地锄草用了18分钟。
C
D
O
A
B
E
八年级 数学
第十四章 一次函数
15
25
37
55
80
0
1.1
2
y/千米
x/分
问题5:玉米地离小明家多远?小明从玉米地走回家的平均速度是多少?
解:由纵坐标看出,玉米地离小明家用2千米,由横坐标看出,小明从玉米回家用了25分钟,由此算出平均速度为0.08千米/分。
D
E
O
A
B
C
1、一天,亮亮发烧了,早晨他烧得厉害,吃过药后感觉好多了,中午时亮亮的体温基本正常,但是下午他的体温又开始上升,直到半夜亮亮才感觉身上不那么烫了,如图所示的各图能基本反映亮亮这一天(0—24时)的体温变化情况是( )
C
2.小芳今天到学校参加初中毕业会考,从家里出发走10分到离家500米的地方吃早餐,吃早餐用了20分;再用10分赶到离家1000米的学校参加考试.下列图象中,能反映这一过程的是( ) .
D
A.
x/分
y/米
O
1500
1000
500
10 20 30 40 50
B.
x/分
y/米
O
1500
1000
500
10 20 30 40 50
1500
1000
500
C.
x/分
y/米
O
10 20 30 40 50
D.
x/分
y/米
O
10 20 30 40 50
1500
1000
500
4.龟兔赛跑的故事:
领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉,
当它醒来时,发现乌龟快到终点了,于是急忙追赶,但已
经来不及了,乌龟先到达了终点………现在用S1和S2
分别表示乌龟、兔子所走的路程,t为时间,则下列
图象中,能够表示S 和t之间的函数关系式的是( )
A
B
D
C
C
5、 张老师从家里乘汽车去学校用了1小时,汽车的速度为30千米/小时,在学校办事用了2小时后,骑自行车经过3小时回到家。在直角坐标系中,用x轴表示时间,单位是时,用y轴表示路程,单位是千米,请你大致画出张老师这次去学校办事再返回家的路线图。
x/小时
y/千米
0
1
2
3
4
5
-1
-2
10
20
30
40
6
7
6.甲,乙两同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发.他们离出发地的距离s/km和骑行时间t/h之间的函数关系如图所示,给出下列说法:
A.他们都骑了20km; B.乙在途中停留了0.5h;
C.甲和乙两人同时到达目的地;
D.相遇后,甲的速度小于乙的速度.
根据图象信息,以上说法正确的是 ( )
B
s/km
t/h
A.1个
B.2个
D.4个
C.3个
甲
乙
7.已知某一函数的图象如图所示,根据图象回答下列问题:
(1)确定自变量的取值范围;
解:自变量的取值范围是-4≤X≤4;
(2)求当x=-4,-2,4时y的值是多少?
解:y的值分别是2, -2,0
(3)求当y=0,4时x的值是多少?
解:当y=0时,x的值是-3,-1或4
当y=4时,x=1.5
(4)当x取何值时y的值最大?当x取 何值时y的值最小?
解:当x=1.5时,y的值最大,值为4,
当x=-2时,y的值最小,值为-2。
(5)当x的值在什么范围内时y随x的增大而增大?
当x的值在什么范围内时y随x的增大而减小?
解:当-2 ≤x≤1.5时,y随x的增大而增大;
当-4≤x≤-2或1.5≤x≤4时,y随x的增大而减小。
-5
-4
-3
-2
-1
5
4
3
2
1
-1 0
-2
-3
-4
-5
2
3
4
5
y
1
x
…
-4
-2
0
2
4
…
y
…
2
1
0
-1
-2
…
x
由列表到图象:
例1:某水库的水位在最近的5小时持续上涨,下表记录了这五小时的水位高度。
t/时
0
1
2
3
4
5
y/米
10
10.05
10.10
10.15
10.20
10.25
(1)由记录表推出这5小时中水位高度y(单位:
千米)随时间t(单位:时)变化的函数解析式
,并画出函数图象;
(2)按估计按这种上涨规律还会持续上涨2小时
,预测再过2小时水位高度将达到多少米。
t/时
0
1
2
3
4
5
y/米
10
10.05
10.10
10.15
10.20
10.25
(1)由记录表推出这5小时中水位高度y(单位:米)随时间t(单位:时)变化的函数解析式。
由记录表观察到开始水位高10米,以后每隔1小时,水位升高0.05米,这样的变化规律可以表示为:
y=0.05t+10 (0 ≤t ≤5)
(2)据估计按这种上涨规律还会持续上涨2小时,预测在过2小时水位高度将达到多少米?
y=0.05×7+10 =10.35
2小时后,预计水位高10.35米。
y
10
5
0
10.35
t
7
y=0.05t+10
把函数的图像向右延伸到t=7所对应的位置,也可以估计出这个值
画出函数 y = x + 0.5 的图象
1、列表
x
…
-3
-2
-1
0
1
2
3
…
y
…
-2.5
-1.5
-0.5
0.5
1.5
2.5
3.5
…
解:
2、描点
3、连线
由解析式到图象:
x
y
0
1
2
3
4
5
-1
-2
-3
-4
-5
1
2
3
4
5
-1
6
7
y= x+0.5
(-1, -0.5)
B
A
C
D
(0, 0.5)
(1, 1.5)
(2, 2.5)
y= x+0.5
如何判断一点是否在某个函数的图象上?
.
课堂归纳:
如何仅由解析式判断一点是否在
某个函数的图象上?
若一个点在某个函数图象上,那么这一点的横坐标做自变量时,纵坐标一定是此时的函数值,反之则不在。
3、连线
由解析式画函数图象的步骤:
1、列表
2、描点
列出自变量与函数的对应值表。
注意:自变量的值(满足取值范围),要取适当.
建立直角坐标系,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中数值对应的各点
按照横坐标从小到大的顺序把描出的点用平滑曲线依次连接起来
归纳
.
课堂练习(一):
2.下列四个点中在函数y=2x—3的图象上有( )个。
(1,2) , (3,3) , (—1, —1), (1.5,0)
A.1 B.2 C.3 D.4
B
1、下列各点中,在函数y= 图象上的是( )
A、(—2,—4) B、(4,4)
C、(—2,4) D、(4,2)
D
3、已知点(-1,2)是函数y=kx的图象上的一点,则k= 。
-2
4、点A(1,m)在函数y=2x的图象上,则点的坐标是( )
A、(1,-1) B、(1,2)
C、(1,1) D、(2,1)
B
表示函数关系的方法:
1、解析法:准确地反映了函数与自变量之间的数量关系。
2、列表法:具体地反映了函数与自变量的数值对应关系。
3、图象法:直观地反映了函数随自变量的变化而变化的规律。
归纳
第3课时 函数的表示
一. 像 1 . S=60t; 2. y=10x ; 3. L=10+0.5m
函数关系是用数学式子给出的 (叫解析法)
二. 前面像体检心电图函数关系是用图象给出的
(叫图象法)
三 .前面刘翔的竞赛成绩函数关系是用表格给出的
(叫列表法)
函数的三种表示法
对函数来说,图象法是非常直观的一种表示方法,它能形象的表示函数随自变量的变化而变化的趋势,所以是十分常见且重要的。
图象上每个点的横纵坐标有何实际意义?
你还能从图中看出哪些信息?
下图测温仪记录的图象,它反映了北京的春季某天气温T如何随时间t的变化而变化。
4
14
24
t/小时
8
T/℃
0
-3
你能看出与上图有哪些不同?
一般地,对于一个函数,如果把自变量
与函数的每对对应值分别作为点的横坐标和
纵坐标,那么坐标平面内由这些点组成的图形就是这个函数的图象。
函数的图象的意义:
归纳
八年级 数学
第十四章 一次函数
15
25
37
55
80
0
1.1
2
y/千米
x/分
例1:下面的图象反映的过程是:小明从家里出发去菜地浇水,又去玉米地锄草,然后回家,其中x表示时间,y表示小明离他家的距离。小明家、玉米地、菜地在同一条直线上。请根据图象回答下列问题:
A
D
B
C
E
O
八年级 数学
第十四章 一次函数
15
25
37
55
80
0
1.1
2
y/千米
x/分
问题1:菜地离小明家多远?小明走到菜地用了多少时间?
解:由纵坐标看出,菜地离小明家1.1千米,由横坐标看出,小明从家到菜地用了15分钟。
A
O
B
C
D
E
八年级 数学
第十四章 一次函数
15
25
37
55
80
0
1.1
2
y/千米
x/分
问题2:小明给菜地浇水用了多少时间?
解:由横坐标看出,小明给菜地浇水用了10分钟。
A
B
O
C
D
E
第十四章 一次函数
15
25
37
55
80
0
1.1
2
y/千米
x/分
问题3:菜地离玉米地多远?小明从菜地走到玉米地用了多少时间?
C
B
解:由纵坐标看出,菜地离玉米地0.9千米,由横坐标看出,小明从菜地到玉米地用了12分钟。
O
A
D
E
八年级 数学
第十四章 一次函数
15
25
37
55
80
0
1.1
2
y/千米
x/分
问题4:小明给玉米地锄草用了多少时间?
解:由横坐标看出,小明给玉米地锄草用了18分钟。
C
D
O
A
B
E
八年级 数学
第十四章 一次函数
15
25
37
55
80
0
1.1
2
y/千米
x/分
问题5:玉米地离小明家多远?小明从玉米地走回家的平均速度是多少?
解:由纵坐标看出,玉米地离小明家用2千米,由横坐标看出,小明从玉米回家用了25分钟,由此算出平均速度为0.08千米/分。
D
E
O
A
B
C
1、一天,亮亮发烧了,早晨他烧得厉害,吃过药后感觉好多了,中午时亮亮的体温基本正常,但是下午他的体温又开始上升,直到半夜亮亮才感觉身上不那么烫了,如图所示的各图能基本反映亮亮这一天(0—24时)的体温变化情况是( )
C
2.小芳今天到学校参加初中毕业会考,从家里出发走10分到离家500米的地方吃早餐,吃早餐用了20分;再用10分赶到离家1000米的学校参加考试.下列图象中,能反映这一过程的是( ) .
D
A.
x/分
y/米
O
1500
1000
500
10 20 30 40 50
B.
x/分
y/米
O
1500
1000
500
10 20 30 40 50
1500
1000
500
C.
x/分
y/米
O
10 20 30 40 50
D.
x/分
y/米
O
10 20 30 40 50
1500
1000
500
4.龟兔赛跑的故事:
领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉,
当它醒来时,发现乌龟快到终点了,于是急忙追赶,但已
经来不及了,乌龟先到达了终点………现在用S1和S2
分别表示乌龟、兔子所走的路程,t为时间,则下列
图象中,能够表示S 和t之间的函数关系式的是( )
A
B
D
C
C
5、 张老师从家里乘汽车去学校用了1小时,汽车的速度为30千米/小时,在学校办事用了2小时后,骑自行车经过3小时回到家。在直角坐标系中,用x轴表示时间,单位是时,用y轴表示路程,单位是千米,请你大致画出张老师这次去学校办事再返回家的路线图。
x/小时
y/千米
0
1
2
3
4
5
-1
-2
10
20
30
40
6
7
6.甲,乙两同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发.他们离出发地的距离s/km和骑行时间t/h之间的函数关系如图所示,给出下列说法:
A.他们都骑了20km; B.乙在途中停留了0.5h;
C.甲和乙两人同时到达目的地;
D.相遇后,甲的速度小于乙的速度.
根据图象信息,以上说法正确的是 ( )
B
s/km
t/h
A.1个
B.2个
D.4个
C.3个
甲
乙
7.已知某一函数的图象如图所示,根据图象回答下列问题:
(1)确定自变量的取值范围;
解:自变量的取值范围是-4≤X≤4;
(2)求当x=-4,-2,4时y的值是多少?
解:y的值分别是2, -2,0
(3)求当y=0,4时x的值是多少?
解:当y=0时,x的值是-3,-1或4
当y=4时,x=1.5
(4)当x取何值时y的值最大?当x取 何值时y的值最小?
解:当x=1.5时,y的值最大,值为4,
当x=-2时,y的值最小,值为-2。
(5)当x的值在什么范围内时y随x的增大而增大?
当x的值在什么范围内时y随x的增大而减小?
解:当-2 ≤x≤1.5时,y随x的增大而增大;
当-4≤x≤-2或1.5≤x≤4时,y随x的增大而减小。
-5
-4
-3
-2
-1
5
4
3
2
1
-1 0
-2
-3
-4
-5
2
3
4
5
y
1
x
…
-4
-2
0
2
4
…
y
…
2
1
0
-1
-2
…
x
由列表到图象:
例1:某水库的水位在最近的5小时持续上涨,下表记录了这五小时的水位高度。
t/时
0
1
2
3
4
5
y/米
10
10.05
10.10
10.15
10.20
10.25
(1)由记录表推出这5小时中水位高度y(单位:
千米)随时间t(单位:时)变化的函数解析式
,并画出函数图象;
(2)按估计按这种上涨规律还会持续上涨2小时
,预测再过2小时水位高度将达到多少米。
t/时
0
1
2
3
4
5
y/米
10
10.05
10.10
10.15
10.20
10.25
(1)由记录表推出这5小时中水位高度y(单位:米)随时间t(单位:时)变化的函数解析式。
由记录表观察到开始水位高10米,以后每隔1小时,水位升高0.05米,这样的变化规律可以表示为:
y=0.05t+10 (0 ≤t ≤5)
(2)据估计按这种上涨规律还会持续上涨2小时,预测在过2小时水位高度将达到多少米?
y=0.05×7+10 =10.35
2小时后,预计水位高10.35米。
y
10
5
0
10.35
t
7
y=0.05t+10
把函数的图像向右延伸到t=7所对应的位置,也可以估计出这个值
画出函数 y = x + 0.5 的图象
1、列表
x
…
-3
-2
-1
0
1
2
3
…
y
…
-2.5
-1.5
-0.5
0.5
1.5
2.5
3.5
…
解:
2、描点
3、连线
由解析式到图象:
x
y
0
1
2
3
4
5
-1
-2
-3
-4
-5
1
2
3
4
5
-1
6
7
y= x+0.5
(-1, -0.5)
B
A
C
D
(0, 0.5)
(1, 1.5)
(2, 2.5)
y= x+0.5
如何判断一点是否在某个函数的图象上?
.
课堂归纳:
如何仅由解析式判断一点是否在
某个函数的图象上?
若一个点在某个函数图象上,那么这一点的横坐标做自变量时,纵坐标一定是此时的函数值,反之则不在。
3、连线
由解析式画函数图象的步骤:
1、列表
2、描点
列出自变量与函数的对应值表。
注意:自变量的值(满足取值范围),要取适当.
建立直角坐标系,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中数值对应的各点
按照横坐标从小到大的顺序把描出的点用平滑曲线依次连接起来
归纳
.
课堂练习(一):
2.下列四个点中在函数y=2x—3的图象上有( )个。
(1,2) , (3,3) , (—1, —1), (1.5,0)
A.1 B.2 C.3 D.4
B
1、下列各点中,在函数y= 图象上的是( )
A、(—2,—4) B、(4,4)
C、(—2,4) D、(4,2)
D
3、已知点(-1,2)是函数y=kx的图象上的一点,则k= 。
-2
4、点A(1,m)在函数y=2x的图象上,则点的坐标是( )
A、(1,-1) B、(1,2)
C、(1,1) D、(2,1)
B
表示函数关系的方法:
1、解析法:准确地反映了函数与自变量之间的数量关系。
2、列表法:具体地反映了函数与自变量的数值对应关系。
3、图象法:直观地反映了函数随自变量的变化而变化的规律。
归纳
