湘教版数学八年级下册 1.4角平分线的性质(2) 课件(14张)
文档属性
| 名称 | 湘教版数学八年级下册 1.4角平分线的性质(2) 课件(14张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 287.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-14 00:00:00 | ||
图片预览


文档简介
1、4角平分线的性质(2)
复习:
1、角平分线的性质定理是: 。
2、角平分线的判定定理是: 。
一、导入明标
角平分线上的点到角的两边的距离相等 .
在一个角的内部,到一个角的两边距离相等的点,在这个角的平分线上。
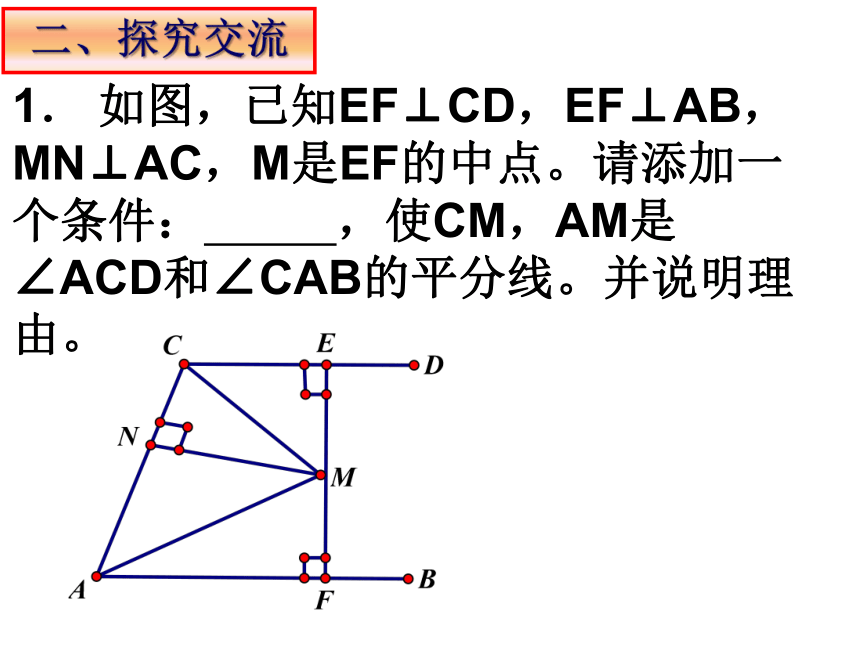
二、探究交流
1. 如图,已知EF⊥CD,EF⊥AB,MN⊥AC,M是EF的中点。请添加一个条件: ,使CM,AM是∠ACD和∠CAB的平分线。并说明理由。
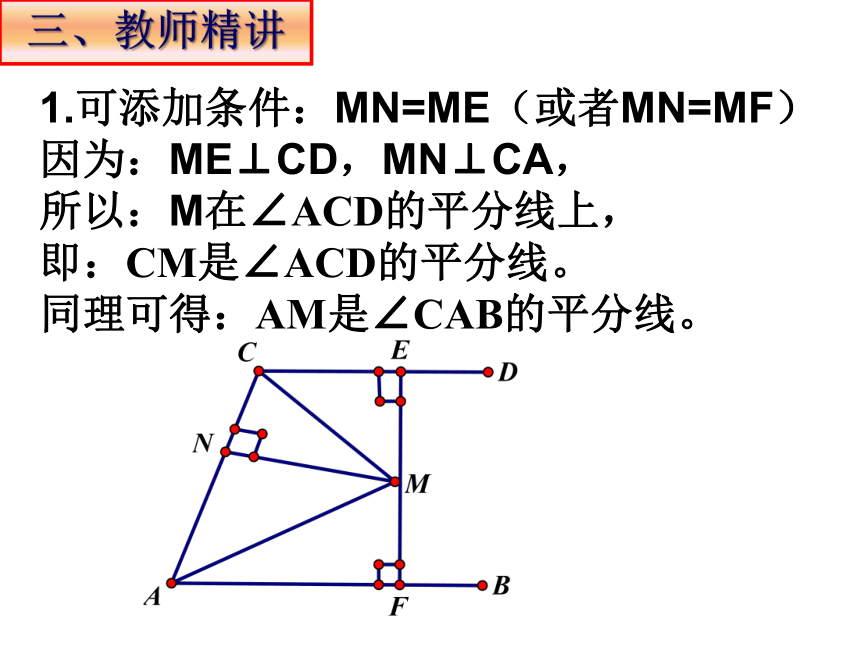
三、教师精讲
1.可添加条件:MN=ME(或者MN=MF)
因为:ME⊥CD,MN⊥CA,
所以:M在∠ACD的平分线上,
即:CM是∠ACD的平分线。
同理可得:AM是∠CAB的平分线。
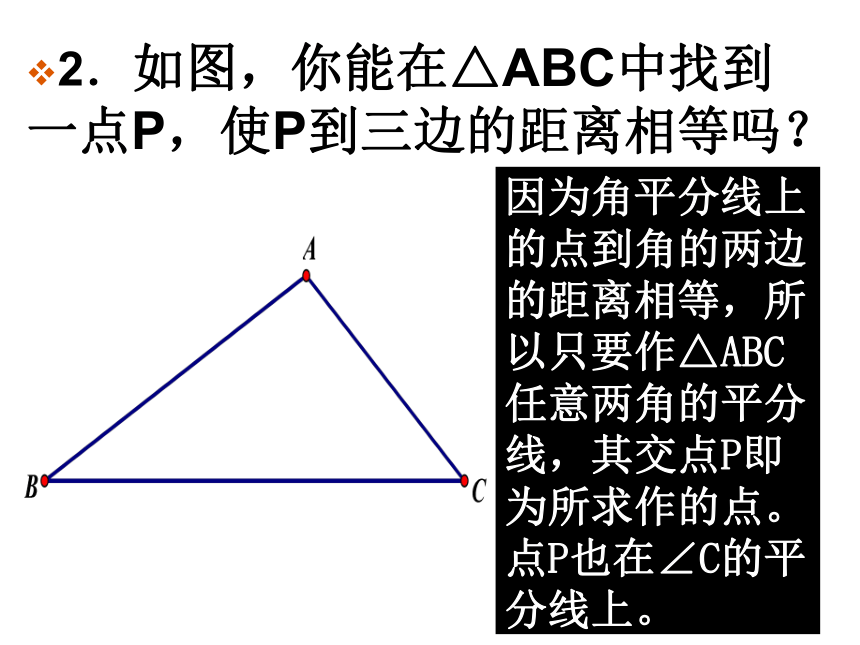
2.如图,你能在△ABC中找到一点P,使P到三边的距离相等吗?
因为角平分线上的点到角的两边的距离相等,所以只要作△ABC任意两角的平分线,其交点P即为所求作的点。点P也在∠C的平分线上。
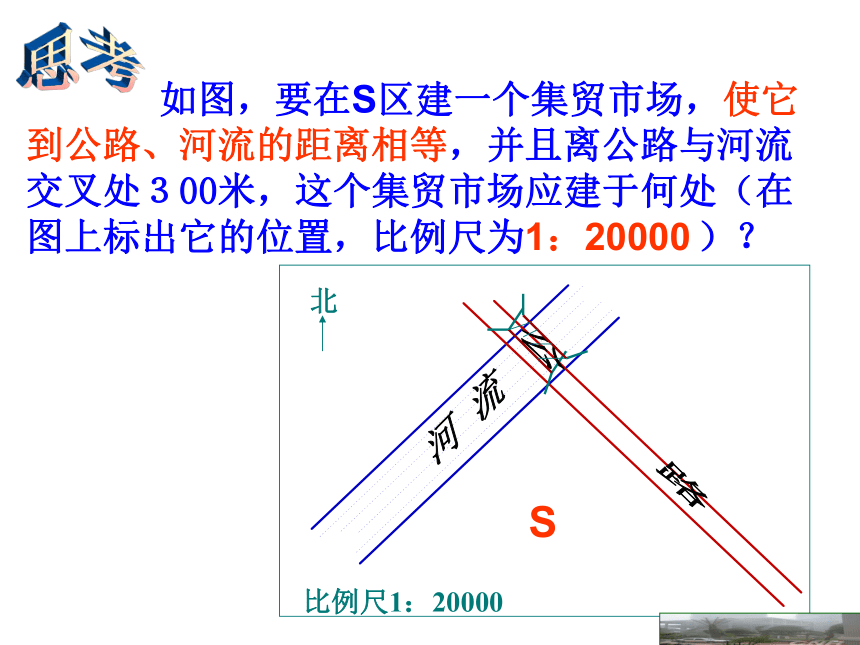
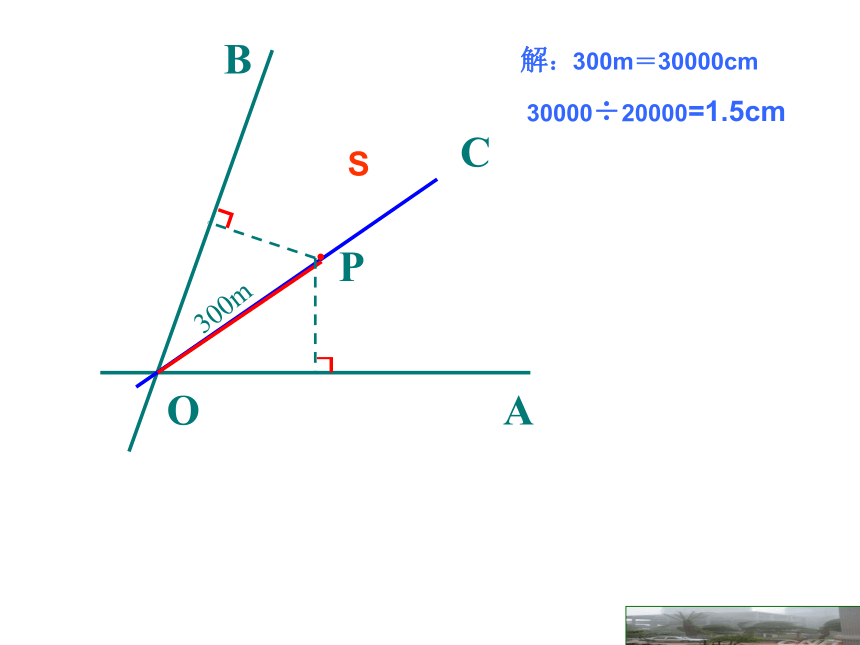
如图,要在S区建一个集贸市场,使它到公路、河流的距离相等,并且离公路与河流交叉处300米,这个集贸市场应建于何处(在图上标出它的位置,比例尺为1:20000 )?
北
比例尺1:20000
河 流
公 路
S
思考
·
O
A
B
C
P
300m
┒
┓
S
解:300m=30000cm
30000÷20000=1.5cm
应用
1
例1.已知:如图,∠C=900,∠B=300,
AD是Rt△ABC的角平分线.
求证:BD=2CD.
A
B
C
D
E
例:已知:如图,∠C= ∠C′=90° ,AC=AC ′ .
求证(1) ∠ABC= ∠ABC ′ ;(2)BC=BC ′ .(要求不用三角形全等的判定)
B
C
A
C′
例1. 如图,在△ABC的外角∠DAC的平分线上任取一点P,作PE⊥DB,PF⊥AC,垂足分别为点E,F。试探索BE+PF与PB的大小关系。
D
D
解:因为AP是∠DAC的平分线,又PE⊥DB,PF⊥AC,
所以,PE=PF,
在△EBP中,BE+PE>PB,
所以:BE+PF>PB。
练习1.如图:在△ABC中,D是BC中点,DE⊥AB,DF⊥AC,垂足分别是E,F,BE=CF。求证:AD是△ABC的角平分线。
练习2.在Rt△ABC中,AC=BC,
∠C=90°,AD平分∠BAC,DF⊥AB于点。
求证:BD+DF=AC。
挑战自我
1.如图,在△ABC中,已知AC=BC,∠C=900,AD是△ABC的角平分线,DE⊥AB,垂足为E.
(1)如果CD=4cm,AC的长
(2)求证:AB=AC+CD.
E
D
A
B
C
复习:
1、角平分线的性质定理是: 。
2、角平分线的判定定理是: 。
一、导入明标
角平分线上的点到角的两边的距离相等 .
在一个角的内部,到一个角的两边距离相等的点,在这个角的平分线上。
二、探究交流
1. 如图,已知EF⊥CD,EF⊥AB,MN⊥AC,M是EF的中点。请添加一个条件: ,使CM,AM是∠ACD和∠CAB的平分线。并说明理由。
三、教师精讲
1.可添加条件:MN=ME(或者MN=MF)
因为:ME⊥CD,MN⊥CA,
所以:M在∠ACD的平分线上,
即:CM是∠ACD的平分线。
同理可得:AM是∠CAB的平分线。
2.如图,你能在△ABC中找到一点P,使P到三边的距离相等吗?
因为角平分线上的点到角的两边的距离相等,所以只要作△ABC任意两角的平分线,其交点P即为所求作的点。点P也在∠C的平分线上。
如图,要在S区建一个集贸市场,使它到公路、河流的距离相等,并且离公路与河流交叉处300米,这个集贸市场应建于何处(在图上标出它的位置,比例尺为1:20000 )?
北
比例尺1:20000
河 流
公 路
S
思考
·
O
A
B
C
P
300m
┒
┓
S
解:300m=30000cm
30000÷20000=1.5cm
应用
1
例1.已知:如图,∠C=900,∠B=300,
AD是Rt△ABC的角平分线.
求证:BD=2CD.
A
B
C
D
E
例:已知:如图,∠C= ∠C′=90° ,AC=AC ′ .
求证(1) ∠ABC= ∠ABC ′ ;(2)BC=BC ′ .(要求不用三角形全等的判定)
B
C
A
C′
例1. 如图,在△ABC的外角∠DAC的平分线上任取一点P,作PE⊥DB,PF⊥AC,垂足分别为点E,F。试探索BE+PF与PB的大小关系。
D
D
解:因为AP是∠DAC的平分线,又PE⊥DB,PF⊥AC,
所以,PE=PF,
在△EBP中,BE+PE>PB,
所以:BE+PF>PB。
练习1.如图:在△ABC中,D是BC中点,DE⊥AB,DF⊥AC,垂足分别是E,F,BE=CF。求证:AD是△ABC的角平分线。
练习2.在Rt△ABC中,AC=BC,
∠C=90°,AD平分∠BAC,DF⊥AB于点。
求证:BD+DF=AC。
挑战自我
1.如图,在△ABC中,已知AC=BC,∠C=900,AD是△ABC的角平分线,DE⊥AB,垂足为E.
(1)如果CD=4cm,AC的长
(2)求证:AB=AC+CD.
E
D
A
B
C
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
