人教版数学八年级上册12.2【三角形全等的判定】期末巩固复习专练(word无答案)
文档属性
| 名称 | 人教版数学八年级上册12.2【三角形全等的判定】期末巩固复习专练(word无答案) | 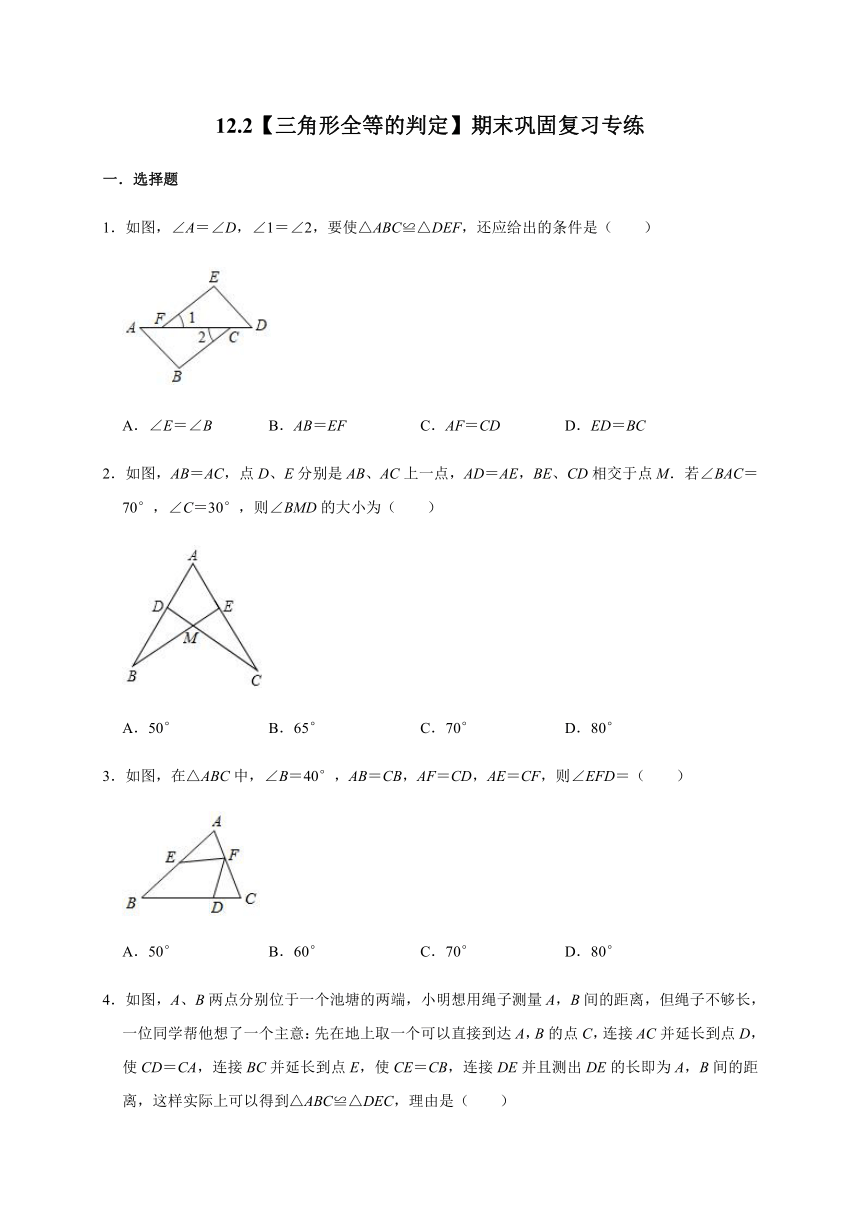 | |
| 格式 | zip | ||
| 文件大小 | 78.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-13 23:20:28 | ||
图片预览



文档简介
12.2【三角形全等的判定】期末巩固复习专练
一.选择题
1.如图,∠A=∠D,∠1=∠2,要使△ABC≌△DEF,还应给出的条件是( )
A.∠E=∠B
B.AB=EF
C.AF=CD
D.ED=BC
2.如图,AB=AC,点D、E分别是AB、AC上一点,AD=AE,BE、CD相交于点M.若∠BAC=70°,∠C=30°,则∠BMD的大小为( )
A.50°
B.65°
C.70°
D.80°
3.如图,在△ABC中,∠B=40°,AB=CB,AF=CD,AE=CF,则∠EFD=( )
A.50°
B.60°
C.70°
D.80°
4.如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,连接AC并延长到点D,使CD=CA,连接BC并延长到点E,使CE=CB,连接DE并且测出DE的长即为A,B间的距离,这样实际上可以得到△ABC≌△DEC,理由是( )
A.SSS
B.AAS
C.ASA
D.SAS
5.如图,在Rt△ABC中,∠ACB=90°,BC=5cm,在AC上取一点E,使EC=BC,过点E作EF⊥AC,连接CF,使CF=AB,若EF=12cm,则下列结论不正确的是( )
A.∠F=∠BCF
B.AE=7cm
C.EF平分AB
D.AB⊥CF
6.根据下列条件,能画出唯一△ABC的是( )
A.AB=3,BC=4,CA=7
B.AC=4,BC=6,∠A=60°
C.∠A=45°,∠B=60°,∠C=75°
D.AB=5,BC=4,∠C=90°
7.下列说法不正确的是( )
A.三边分别相等的两个三角形全等
B.有两边及一角对应相等的两个三角形全等
C.有两角及一边对应相等的两个三角形全等
D.斜边和一条直角边分别相等的两个直角三角形全等
8.如图,在△ABC和△DEC中,已知CB=CE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )
A.AB=DE,∠B=∠E
B.AB=DE,AC=DC
C.AB=DE,∠A=∠D
D.∠A=∠D,∠B=∠E
9.在△ABC中,AB=5,AC=3,AD为BC边的中线,则AD的长x的取值范围( )
A.5≤x≤8
B.4≤x≤7
C.1<x<4
D.
10.如图,△ABC中,D为BC的中点,点E为BA延长线上一点,DF⊥DE交射线AC于点F,连接EF,则BE+CF与EF的大小关系为( )
A.BE+CF<EF
B.BE+CF=EF
C.BE+CF>EF
D.以上都有可能
二.填空题
11.如图,点A,E,B,F在同一直线上,AC=FD,BC=ED,请添加一个条件
,使△ABC≌△FED.
12.如图,在△ABC中,AD是BC边上的高,BE是AC边上的高,且AD,BE交于点F,若BF=AC,CD=3,BD=8,则线段AF的长度为
.
13.如图,四边形ABCD中,∠BAD=∠C=90°,AB=AD,AE⊥BC,垂足为E,若线段AE=3,则四边形ABCD的面积是
.
14.如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,AD=2cm,BE=0.5cm,则DE=
cm.
15.如图,在Rt△ABC中,∠C=90°,AC=10,BC=5,线段PQ=AB,P,Q两点分别在线段AC和过点A且垂直于AC的射线AO上运动,当AP=
时,△ABC和△PQA全等.
三.解答题
16.如图,四边形ABCD中,AB=AD,AC、BD是对角线,∠1=∠2.
(1)求证:△ABC≌△ADC;
(2)判断△BCD的形状并说明.
17.如图,在△ABC与△CDE中,点C在线段BD上,且AB⊥BD,DE⊥BD,AC=CE,BC=DE.
(1)求证:BD=AB+DE.
(2)求∠ACE的度数.
18.如图,在四边形ABCD中,AD∥BC,E为AC的中点,连接DE并延长,交BC于点F.
(1)求证:DE=EF;
(2)若AD=12,BF:CF=2:3,求BC的长.
19.如图,△ABF中,E是边AF的中点,点C在BF上,作AD∥BF交CE的延长线于点D.
(1)求证:△ADE≌△FCE.
(2)若∠CEF=90°,AD=5,CE=4,求点E到BF的距离.
20.如图,AE与BD相交于点C,AC=EC,BC=DC,AB=4cm,点P从点A出发,沿A→B→A方向以3cm/s的速度运动,点Q从点D出发,沿D→E方向以1cm/s的速度运动,P、Q两点同时出发.当点P到达点A时,P、Q两点同时停止运动.设点P的运动时间为t(s).
(1)求证:AB∥DE.
(2)写出线段AP的长(用含t的式子表示).
(3)连结PQ,当线段PQ经过点C时,求t的值.
一.选择题
1.如图,∠A=∠D,∠1=∠2,要使△ABC≌△DEF,还应给出的条件是( )
A.∠E=∠B
B.AB=EF
C.AF=CD
D.ED=BC
2.如图,AB=AC,点D、E分别是AB、AC上一点,AD=AE,BE、CD相交于点M.若∠BAC=70°,∠C=30°,则∠BMD的大小为( )
A.50°
B.65°
C.70°
D.80°
3.如图,在△ABC中,∠B=40°,AB=CB,AF=CD,AE=CF,则∠EFD=( )
A.50°
B.60°
C.70°
D.80°
4.如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,连接AC并延长到点D,使CD=CA,连接BC并延长到点E,使CE=CB,连接DE并且测出DE的长即为A,B间的距离,这样实际上可以得到△ABC≌△DEC,理由是( )
A.SSS
B.AAS
C.ASA
D.SAS
5.如图,在Rt△ABC中,∠ACB=90°,BC=5cm,在AC上取一点E,使EC=BC,过点E作EF⊥AC,连接CF,使CF=AB,若EF=12cm,则下列结论不正确的是( )
A.∠F=∠BCF
B.AE=7cm
C.EF平分AB
D.AB⊥CF
6.根据下列条件,能画出唯一△ABC的是( )
A.AB=3,BC=4,CA=7
B.AC=4,BC=6,∠A=60°
C.∠A=45°,∠B=60°,∠C=75°
D.AB=5,BC=4,∠C=90°
7.下列说法不正确的是( )
A.三边分别相等的两个三角形全等
B.有两边及一角对应相等的两个三角形全等
C.有两角及一边对应相等的两个三角形全等
D.斜边和一条直角边分别相等的两个直角三角形全等
8.如图,在△ABC和△DEC中,已知CB=CE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )
A.AB=DE,∠B=∠E
B.AB=DE,AC=DC
C.AB=DE,∠A=∠D
D.∠A=∠D,∠B=∠E
9.在△ABC中,AB=5,AC=3,AD为BC边的中线,则AD的长x的取值范围( )
A.5≤x≤8
B.4≤x≤7
C.1<x<4
D.
10.如图,△ABC中,D为BC的中点,点E为BA延长线上一点,DF⊥DE交射线AC于点F,连接EF,则BE+CF与EF的大小关系为( )
A.BE+CF<EF
B.BE+CF=EF
C.BE+CF>EF
D.以上都有可能
二.填空题
11.如图,点A,E,B,F在同一直线上,AC=FD,BC=ED,请添加一个条件
,使△ABC≌△FED.
12.如图,在△ABC中,AD是BC边上的高,BE是AC边上的高,且AD,BE交于点F,若BF=AC,CD=3,BD=8,则线段AF的长度为
.
13.如图,四边形ABCD中,∠BAD=∠C=90°,AB=AD,AE⊥BC,垂足为E,若线段AE=3,则四边形ABCD的面积是
.
14.如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,AD=2cm,BE=0.5cm,则DE=
cm.
15.如图,在Rt△ABC中,∠C=90°,AC=10,BC=5,线段PQ=AB,P,Q两点分别在线段AC和过点A且垂直于AC的射线AO上运动,当AP=
时,△ABC和△PQA全等.
三.解答题
16.如图,四边形ABCD中,AB=AD,AC、BD是对角线,∠1=∠2.
(1)求证:△ABC≌△ADC;
(2)判断△BCD的形状并说明.
17.如图,在△ABC与△CDE中,点C在线段BD上,且AB⊥BD,DE⊥BD,AC=CE,BC=DE.
(1)求证:BD=AB+DE.
(2)求∠ACE的度数.
18.如图,在四边形ABCD中,AD∥BC,E为AC的中点,连接DE并延长,交BC于点F.
(1)求证:DE=EF;
(2)若AD=12,BF:CF=2:3,求BC的长.
19.如图,△ABF中,E是边AF的中点,点C在BF上,作AD∥BF交CE的延长线于点D.
(1)求证:△ADE≌△FCE.
(2)若∠CEF=90°,AD=5,CE=4,求点E到BF的距离.
20.如图,AE与BD相交于点C,AC=EC,BC=DC,AB=4cm,点P从点A出发,沿A→B→A方向以3cm/s的速度运动,点Q从点D出发,沿D→E方向以1cm/s的速度运动,P、Q两点同时出发.当点P到达点A时,P、Q两点同时停止运动.设点P的运动时间为t(s).
(1)求证:AB∥DE.
(2)写出线段AP的长(用含t的式子表示).
(3)连结PQ,当线段PQ经过点C时,求t的值.
