6.3 余角 补角 对顶角 课件1

(共14张PPT)
*
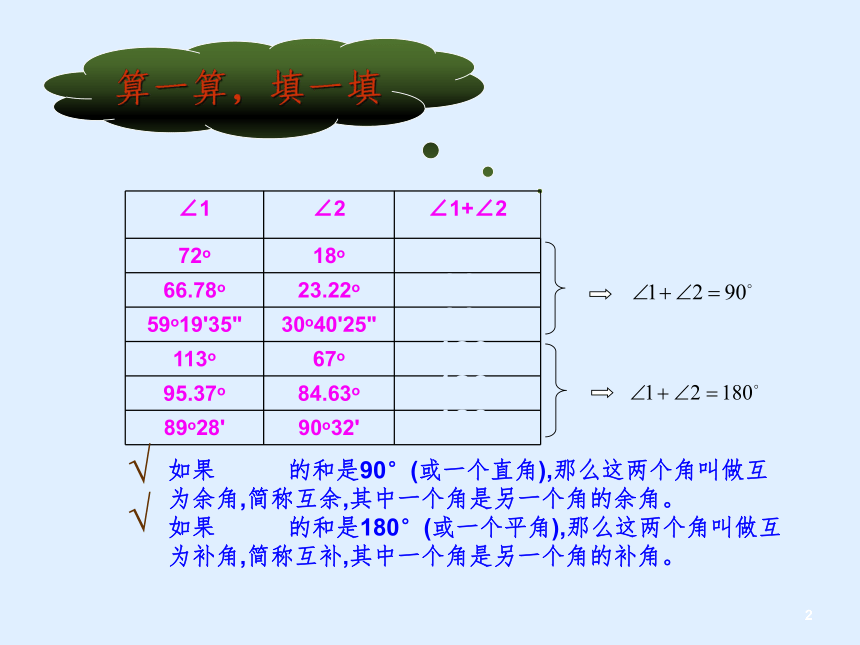
算一算，填一填
∠1 ∠2 ∠1+∠2
72o 18o
66.78o 23.22o
59o19'35" 30o40'25"
113o 67o
95.37o 84.63o
89o28' 90o32'
90o
90o
90o
180o
180o
180o
如果两个角的和是90°(或一个直角),那么这两个角叫做互为余角,简称互余,其中一个角是另一个角的余角。
如果两个角的和是180°(或一个平角),那么这两个角叫做互为补角,简称互补,其中一个角是另一个角的补角。
√
√
*
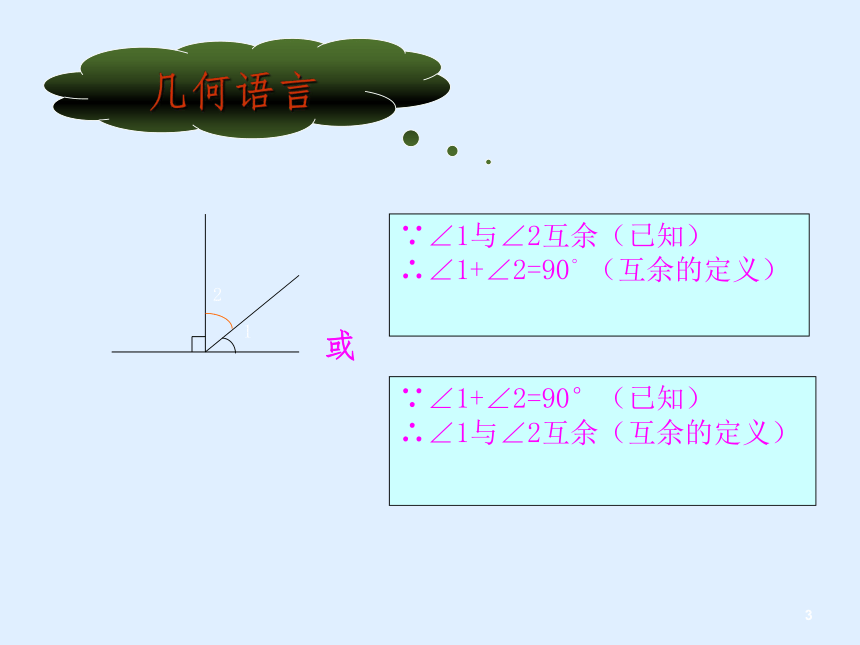
几何语言
2
1
∵∠1与∠2互余（已知）
∴∠1+∠2=90°（互余的定义）
∵∠1+∠2=90°（已知）
∴∠1与∠2互余（互余的定义）
或
*
例1．已知∠A=34o30′，求∠A的余角、补角。
解：∠A的余角=90o-∠A =90o-34o30' =55o30' ∠A的补角=180o-∠A =180o-34o30' =145o30'
变式：(1)已知∠A的补角是75o,求∠A (2)已知∠A的余角是37o,求∠A及∠A的补角。
*
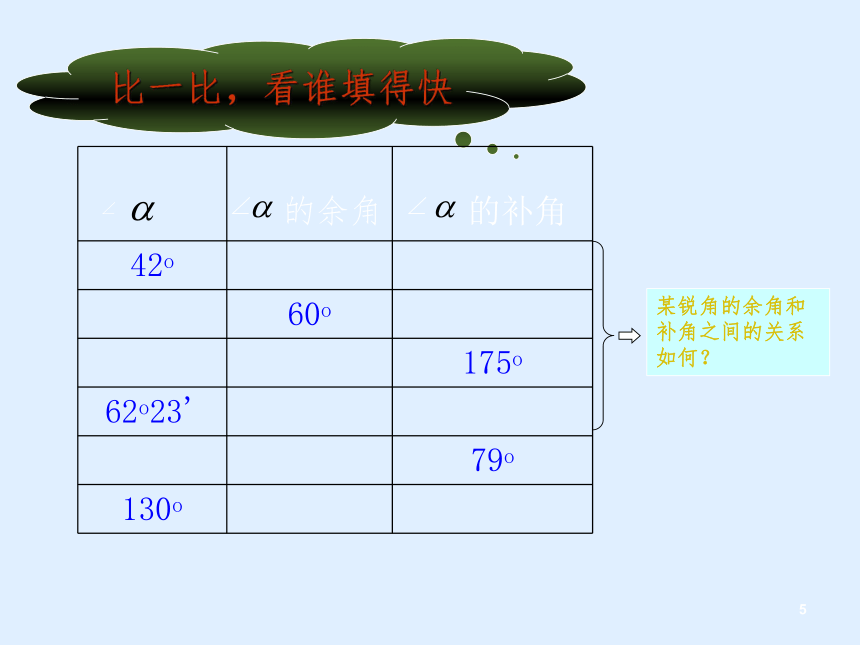
比一比，看谁填得快
∠
∠
∠
的余角
的补角
42o
60o
175o
62o23'
79o
130o
48 o
138o
30o
150o
5o
85o
27o37'
117o37 '
101o
无
无
50°
某锐角的余角和补角之间的关系如何？
*
判断：
1．如果∠1=30°，∠2=25°，∠3=35°，那么∠1、∠2、∠3这三个角称为互为余角。（ ）
错
（析：互为余角只是对两个角的数量关系而言的）
2．两块直角三角板中∠A=90°，∠D=90°，它们互为补角。（ ）
对
（析：互为补角仅仅表明两个角的数量关系，而与角的位置无关。 ）
C
A
C
F
D
E
*
例2．已知一个角的补角是这个角的余角的4倍，求这个角的度数。
解：设这个角为x°，则它的余角为(90-x) °，它的补角为(180-x) °，得 180-x=4(90-x) 180-x=360-4x -x+4x=360-18 3x=180 X=60 答：这个角是60o。
*
1．已知∠A的余角是它的2倍，求∠A的度数。
2．已知∠B是它补角的3倍，求∠B的度数。
解：设∠A为x°，则它的余角为(2x)°，得
X+2x=90,x=30°
答：∠A是30°。
解:设∠B为x°则它的补角为(180-x)°得
X=3(180-x), x=135
答：∠B是135°。
*
例3．如图，∠1和∠2互余，∠3和∠4互余，若∠1=∠3，那么∠2与∠4相等吗？为什么？
证明：∵∠1与∠2互余 ∴∠1+∠2=90o，即∠2=90o-∠1 ∵∠3与∠4互余 ∴∠3+∠4=90o，即∠4=90o-∠3 又∵∠1=∠3 ∴∠2=∠4（等量减等量差相等）
例3变式：如果把互余改为互补仍相等吗
为什么？
1
2
4
3
*
1．如图3-1，若∠1与∠2互余，∠2与∠3互余，则∠ （ ）， =∠（ ），根据是 ；
1
2
3
图3-1
图3-2
1
3
2.如图3-2，若∠ 、∠ 互补，∠ 与∠ 互补，则∠ =∠ ，根据是 ；
同角的余角相等
同角的余角相等
*
3．如图3-3，O是直线AB上的一点，OC平分∠AOB，∠DOE=90o，则
（1）∠2=∠（ ），∠1=∠（ ）
（2）图中，互为余角的角共有哪几对？
（ ）
（3）图中，∠DOB的补角是（ ）。
4
3
∠1与∠2，∠1与∠4，∠2与∠3，∠4与∠3
∠1，∠3
A
1
4
3
2
B
C
D
E
*
今天我们学了什么？
1．余角、补角的概念；
2．余角、补角的性质；
3．互余、互补与两个角的数量有关与位置无关；
4．进行简单证明。
*
练习卷课后作业
作业：
*
课后思考:
如图, ∠1与∠2互补,则∠1与 (∠2-∠1)和的关系为( )。
A．互补 B.互余 C.相等 D.小于的度数。
1
2