6.3 余角 补角 对顶角 课件2

(共23张PPT)
1平角=
1直角=
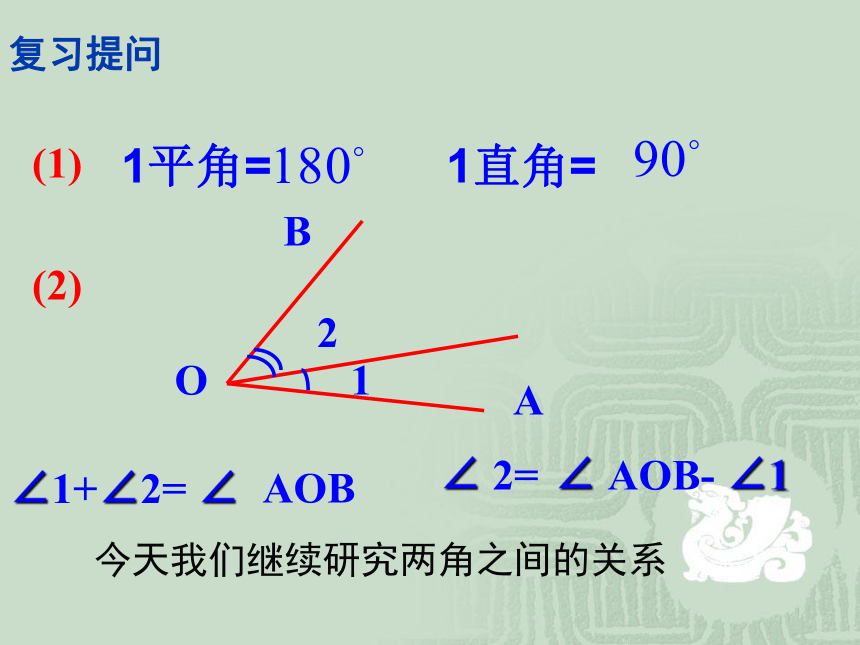
复习提问
∠1+∠2= ∠
AOB
∠ 2=
∠ AOB- ∠1
(1)
B
A
O
2
1
(2)
今天我们继续研究两角之间的关系
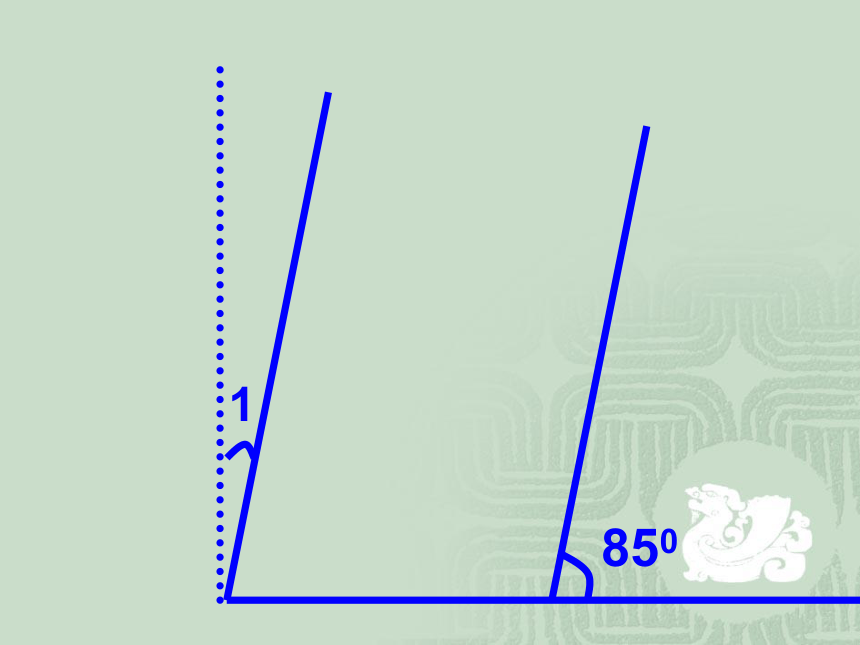
850
1
850
1
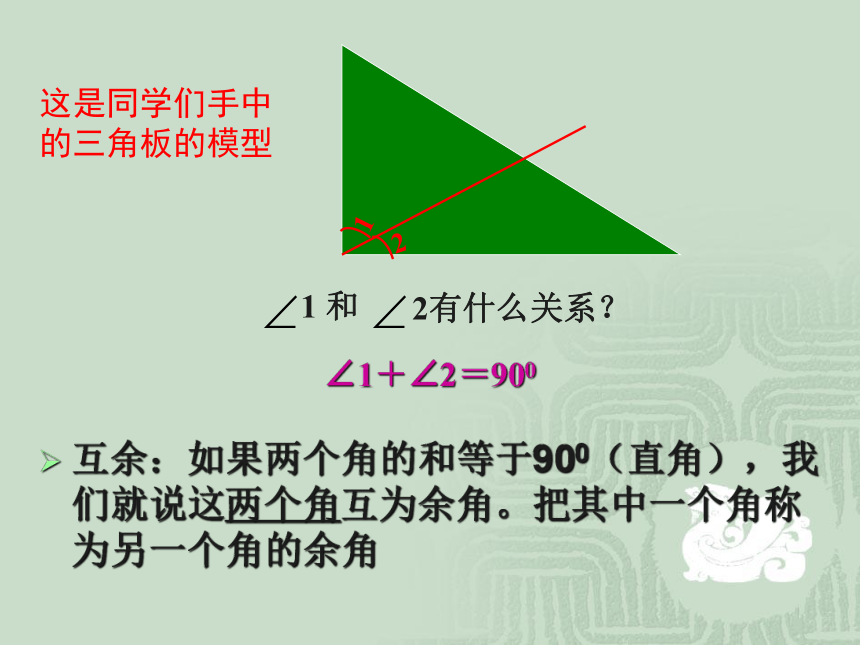
互余：如果两个角的和等于900（直角），我们就说这两个角互为余角。把其中一个角称为另一个角的余角
1 和
2有什么关系？
∠1＋∠2＝900
1
2
这是同学们手中的三角板的模型
如果 1＝300， 2＝250， 3＝350，那么它们互为余角。
互为余角只是对两个角而言的。
1
2
两副直角三角板中， 1＝300， 2＝600,
它们互为余角.
互为余角仅仅表明了两个角的数量关系，而与角的位置关系无关。
（错）
（对）
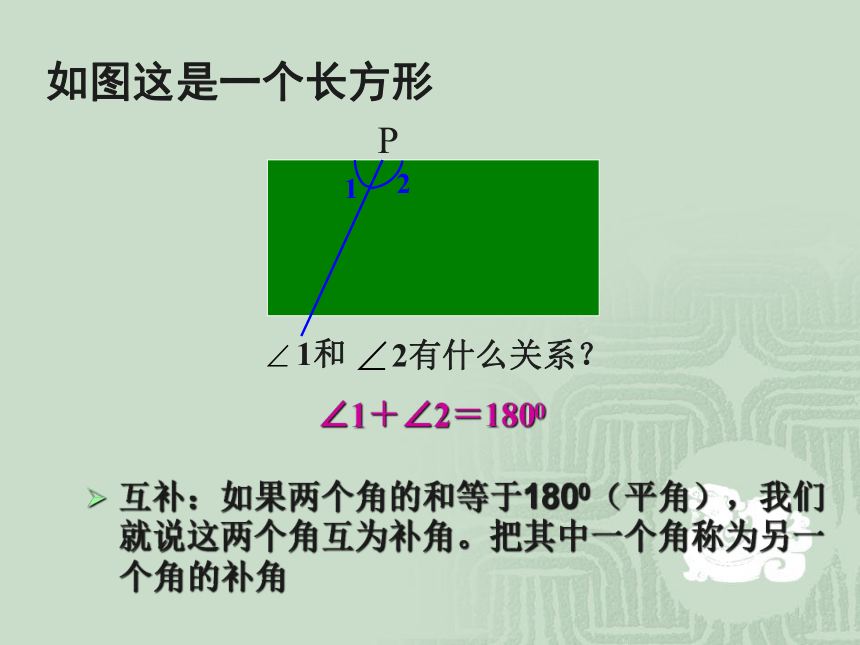
互补：如果两个角的和等于1800（平角），我们就说这两个角互为补角。把其中一个角称为另一个角的补角
2
1
1和
2有什么关系？
∠1＋∠2＝1800
如图这是一个长方形
P
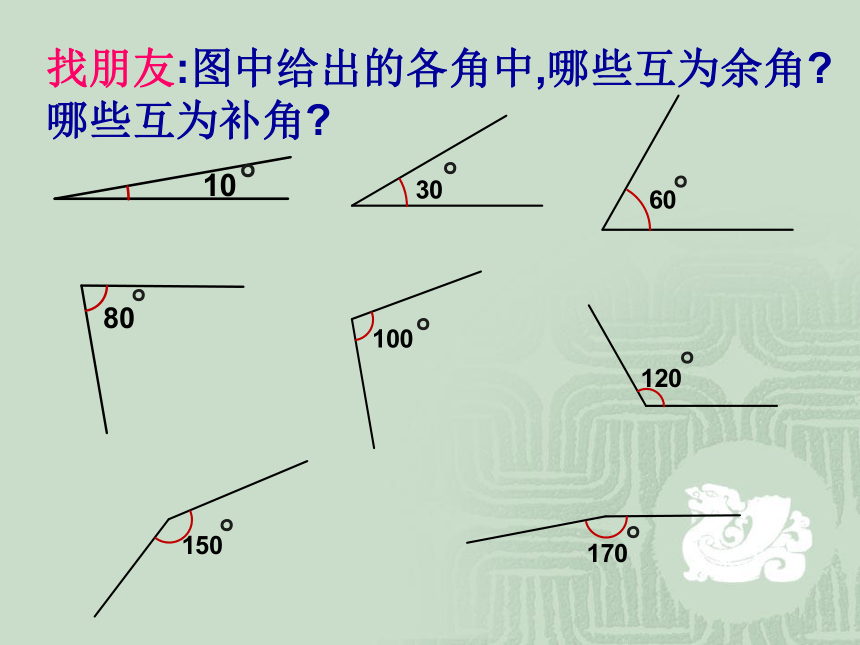
找朋友:图中给出的各角中,哪些互为余角 哪些互为补角
°
°
°
°
°
°
°
°
(1)若
,则
互为补角. ( )
(2)互为余角、互为补角的两个
角一定有公共顶点. ( )
×
×
1.定义中的“互为”是相互的意思.互为余角和互为补角是对两个角来说的.
2.互为余角、互为补角的两个角不一定有公共顶点.
比一比，看谁填得快
角α α的余角 α的补角
500
670
23035'
900
1350
100035'
400
1300
230
1130
66025'
156025'
900
450
79025'
锐角的补角是钝角；
直角的补角是直角；
钝角的补角是锐角。
(1)
（2）若一个角为x度，则它的余角为
________度，它的补角为__________度。
（90-x）
（180-x）
（３）一个角的补角是它余角的3倍，这个角是多少度？
解：设这个角为x度，则它的余角为
（90-x）度，它的补角为（180-x）度
列方程：3（90-x）=180-x
x=45°
答：这个角为 45°.
观察与思考:
(1).∠ADC与∠BDC有相等的关系，你能说明为什么吗？
∵∠1＋∠ADC＝900， ∠2＋∠BDC＝900
∴ ∠ADC＝900－ ∠1， ∠BDC＝900－∠2
又∵ ∠1＝ ∠2
∴ 900－ ∠1＝ 900－∠2
即∠ADC＝ ∠BDC
等角（或同角）的余角相等。
通过刚才的观察，如果∠1＝∠2那么
类似的你能得到等角或同角的补角也相等吗
试一试
如图, ∠1与∠ 2互补, ∠ 3与∠ 4互补,如果∠ 1= ∠ 3,那么∠ 2与∠ 4相等吗 为什么
2
1
3
4
等角（或同角）的补角相等
练一练:在下列图形中找出一组相等的角,你会用几何语言叙述为什么吗
一副三角板本身就蕴含着相等和互余，用一副三角板还能构造出其它一些图形，其中蕴含着相等、互余或者是互补的角，请大家动手尝试，构造设计一些这样的图形.
知识应用
数学小知识
打台球时，球的反射角总是等于入射角.
入射角
反射角
O
back
学以致用：如果∠5=40°,那么∠1应等于多少度,才能保证蓝色球准确入袋？请说明理由.
6
7
8
9
40°
今天我们学了什么？
（1）余角、补角的概念
注意：余角、补角与两个角的大小有关系，与它们的位置没有关系。
（2）余角、补角的性质
等角(或同角）的余角相等；
等角（或同角）的补角相等。
作业
数学补充习题P82
一个角的补角是它余角的4倍，这个角是多少度？
复习本节所学内容
预习余角与补角(二)---方向角