2020—2021学年人教版(2019)高二物理《电磁学习题讨论课:导体和绝缘体》课件38张PPT
文档属性
| 名称 | 2020—2021学年人教版(2019)高二物理《电磁学习题讨论课:导体和绝缘体》课件38张PPT |
|
|
| 格式 | ppt | ||
| 文件大小 | 453.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-02-14 00:00:00 | ||
图片预览












文档简介
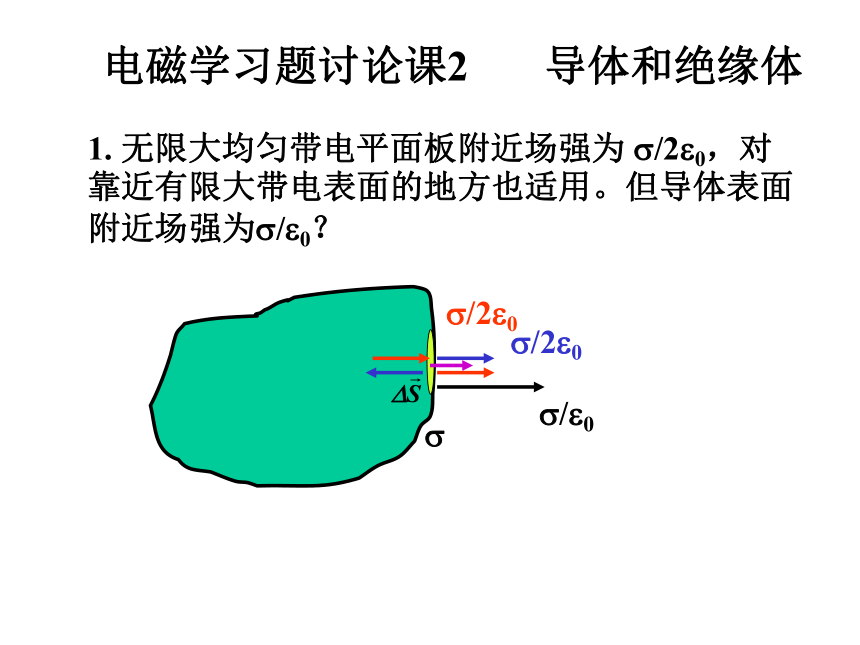
电磁学习题讨论课2 导体和绝缘体
1. 无限大均匀带电平面板附近场强为 ?/2?0,对靠近有限大带电表面的地方也适用。但导体表面附近场强为?/?0?
?
?/2?0
?/?0
?/2?0
2.在一个绝缘的不带电的导体球周围做一同心球面的
高斯面,定性讨论将一正电荷q移向高斯面上A点的过
程,
(1)A点处的场强大小和方向怎样变化?
(2)B点处的场强大小和方向怎样变化?
(3)过S面的电通量怎样变化?
o
B
A
q
电通量不变
+
3.一不接地的球形金属壳不带电,现球心处放一
正电荷q1,在球壳外放一点电荷q2,问:
(1) q2能否感受q1的场的作用;
(2) q1能否感受电场力的作用;
(3) q1在球壳内运动, q2能否感受得到?
若q1数值变化时又如何?
(4) 若将球壳接地以上三问的答案又如何?
q1
q2
(1)能
(2)不能
(3)不能,能
(1)不能
(2)不能
(3)都不能
(4)
4.半径为r1、r2( r2 >r1)的互相绝缘的二同心导体
球壳,内球壳带电+q,外球壳带电Q,问:
(1)外球壳的电荷和电势;
(2)外球壳接地后重新绝缘,外球壳的电荷和电势;
(3)然后内球壳接地,内球壳的电势和外球壳的电
势和(2)相比各改变了多少?
(1)无限远处电势为零
电荷Q+q
r1
r2
q
Q
解:
-q
+q
壳厚度远小于半径
(2)外球壳接地,球壳外电场为零,q+Q电荷流
入大地,外球壳带电 -q,电势为零。
(3)内球壳接地,剩余电荷
r1
r2
q
-q
(2)
r1
r2
-q
(3)
内球壳电势
外球壳电势
r1
r2
-q
5.一绝缘导体球不带电,距球心 r 处放一点电荷q,
求导体电势。
导体为等势体,能求得球心o处的电势即可。
导体上感应电荷都在球表面,距球心R
电荷守恒
解:
q
r
o
R
6.一球形电容器内、外导体球壳A和B的半径R1和R3,两球壳间充满两层球壳形的均匀各向同性介质?1、 ?2,两介质分层处半径R2,内球壳带电Q,外球壳接地,求:
(1)两介质区的电场E=?
(2)四个界面上的束缚面电荷密度?=?
(3)电容C=?
R3
R2
R1
?2
?1
A
B
Q
(1)
解:
R3
R2
R1
?2
?1
A
B
Q
(2)
(3) C=Q/U
R3
R2
R1
?2
?1
A
B
Q
7 . 在均匀外电场 处,一介质球,半径为R,
相对介电常数为?r,被均匀极化,求:
(1)极化面电荷密度;(2)极化球的内部电场;
(3)极化强度 (4)中垂线距球心r处电场。
R
(1)
(2)
球心处由极化电荷产生电场方向如图。
+
-
(3)
(4)
等于球内电场
r
R
r
特殊情况
?连线上,正电荷右侧一点 P 的场强
?垂直连线上的一点
9.带电为Q的导体薄球壳(可看成球面)
半径为R,壳内中心处有点电荷q,
已知球壳电势为Ua,则壳内任一点P
的电势为
对不对?
【解】
根据电势叠加原理
q
Q
R
P
r
P点的电势为
q
Q
R
P
r
球壳的电势为
为什么不对?
原来Ua并不是Q单独存在时的电势。
电势叠加:
(结果一样)
方法二:
方法三:
结论是
(结果相同)
11.今有两个电容值均为C的电容器,其带
电量分别为Q和2Q,求两电容器在并联前
后总能量的变化?
C
C
+Q
+2Q
-2Q
-Q
前
C
+3Q
-3Q
C
后
【解】
并联前
并联后
电容为2C,
带电量为3Q
C
+Q
-Q
C
+2Q
-2Q
后
为什么能量减少了?能量到哪里去了?
问题是:并联以后两个电容器上的
电量还是原来的分布吗?
设
C
+q1
-q1
C
+q2
-q2
C
+q1
-q1
C
+q2
-q2
求 q1,q2:
由(2)得
由(1)得
C
+1.5Q
-1.5Q
C
+1.5Q
-1.5Q
原来是在电量的流动
过程中,电场的能量
损失掉了一些。
R
铜球
?r
13.黄铜球浮在相对介电常数为? r=3.0 的
大油槽中,球的一半浸在油中,球的
上半部在空气中,如图所示。
已知球上净电荷为 Q =2.0?10-6C,
(1)求球的上、下部分各有多少自由电荷?
(2)求下半球表面附近极化电荷的?’、q’?
R
铜球
?r
因为铜球是等势体,所以可以看成是空气
中的半球电容器和油为介质的半球电容器
并联:
(1)求球的上、下
部分各有多少
自由电荷?
【解】
……
(2)
……
(1)
得
可以解得
(2)求下半球表面附近极化电荷的?’、q’?
?r
R
铜球
S
作半球形高斯面 S 如图:
高斯定理
此 ?’、q’ 即为所求。
就有
可知
R
Q上
Q下
+q’
讨论:
即把极化电荷也算上,
球的上、下部分带电
情况是相同的。
对比
上半空间电场的分布可等效为均匀带电2Q上
的整个球面在空气中的电场分布,
R
铜球
?r
Q上
Q下 +q’= Q上
上半球的电势为
下半空间电场的分布可等效为均匀带电2Q下
的整个球面浸在油中的电场分布,即
由下半球的电势分布公式,还可以看出:
下半球的电势是一样的:
有
3.(P67/1)一绝缘导体球不带电,距球心 r 处放一点电荷+q,
金属球半径R,
求:(1)金属球上感应电荷在球心处产生的电场强度
及此时导体球的电势。
(2) 若将金属球接地,球上的净电荷为何?
导体为等势体,能求得球心o处的电势即可。
o
导体上感应电荷都在球表面,距球心R
电荷守恒
解:(1) 如图,
-
-
-
-
+
+
+
+
+q
接地 即
设:感应电量为
o点的电势为0 则
-
-
-
-
o
+q
(2) 若将金属球接地,球上的净电荷为何?
4(P67/3).带电q、半径为R1的导体球,其外同心放置一导体球壳,
壳内、外半径为R2、R3。
问:1)外球壳的电荷和电势;
2)外球壳接地后重新绝缘,外球壳的电荷和电势;
3)然后内球壳接地,内球的电荷及外球壳的电势。
解(1)无限远处电势为零
高斯定理和电量守恒
等效:三个均匀带电的球面
利用叠加原理
等势体
(2)外球壳接地,球壳外电场为零,q电荷流入大地
球壳内表面带电 -q,外表面:0。
接地后重新绝缘,由高斯定理和电量守恒得:
内表面电荷-q ,外表面:0
等效:两个均匀带电的球面
利用叠加原理
(3)内导体球接地,剩余电荷q′。
外球壳电势
则,壳内表面:-q′
外表面:-q+q′
内球壳电势
6(P72/2).一球形电容器内、外导体球壳A和B的半径R1和R2,
两球壳间充满两层球壳形的均匀各向同性介质?r1、 ?r2,两介质分层处半径R,内球壳带电Q。
求:(1)两介质区的
(2)介质区的电能密度?
(3) 四个界面上的束缚面电荷密度?=?
R2
R
R1
?r2
?r1
A
B
Q
(1)介质区:
R2
R
R1
?r2
?r1
A
B
Q
(2)
(3)
介质
内表面
外表面
介质
内表面
外表面
1. 无限大均匀带电平面板附近场强为 ?/2?0,对靠近有限大带电表面的地方也适用。但导体表面附近场强为?/?0?
?
?/2?0
?/?0
?/2?0
2.在一个绝缘的不带电的导体球周围做一同心球面的
高斯面,定性讨论将一正电荷q移向高斯面上A点的过
程,
(1)A点处的场强大小和方向怎样变化?
(2)B点处的场强大小和方向怎样变化?
(3)过S面的电通量怎样变化?
o
B
A
q
电通量不变
+
3.一不接地的球形金属壳不带电,现球心处放一
正电荷q1,在球壳外放一点电荷q2,问:
(1) q2能否感受q1的场的作用;
(2) q1能否感受电场力的作用;
(3) q1在球壳内运动, q2能否感受得到?
若q1数值变化时又如何?
(4) 若将球壳接地以上三问的答案又如何?
q1
q2
(1)能
(2)不能
(3)不能,能
(1)不能
(2)不能
(3)都不能
(4)
4.半径为r1、r2( r2 >r1)的互相绝缘的二同心导体
球壳,内球壳带电+q,外球壳带电Q,问:
(1)外球壳的电荷和电势;
(2)外球壳接地后重新绝缘,外球壳的电荷和电势;
(3)然后内球壳接地,内球壳的电势和外球壳的电
势和(2)相比各改变了多少?
(1)无限远处电势为零
电荷Q+q
r1
r2
q
Q
解:
-q
+q
壳厚度远小于半径
(2)外球壳接地,球壳外电场为零,q+Q电荷流
入大地,外球壳带电 -q,电势为零。
(3)内球壳接地,剩余电荷
r1
r2
q
-q
(2)
r1
r2
-q
(3)
内球壳电势
外球壳电势
r1
r2
-q
5.一绝缘导体球不带电,距球心 r 处放一点电荷q,
求导体电势。
导体为等势体,能求得球心o处的电势即可。
导体上感应电荷都在球表面,距球心R
电荷守恒
解:
q
r
o
R
6.一球形电容器内、外导体球壳A和B的半径R1和R3,两球壳间充满两层球壳形的均匀各向同性介质?1、 ?2,两介质分层处半径R2,内球壳带电Q,外球壳接地,求:
(1)两介质区的电场E=?
(2)四个界面上的束缚面电荷密度?=?
(3)电容C=?
R3
R2
R1
?2
?1
A
B
Q
(1)
解:
R3
R2
R1
?2
?1
A
B
Q
(2)
(3) C=Q/U
R3
R2
R1
?2
?1
A
B
Q
7 . 在均匀外电场 处,一介质球,半径为R,
相对介电常数为?r,被均匀极化,求:
(1)极化面电荷密度;(2)极化球的内部电场;
(3)极化强度 (4)中垂线距球心r处电场。
R
(1)
(2)
球心处由极化电荷产生电场方向如图。
+
-
(3)
(4)
等于球内电场
r
R
r
特殊情况
?连线上,正电荷右侧一点 P 的场强
?垂直连线上的一点
9.带电为Q的导体薄球壳(可看成球面)
半径为R,壳内中心处有点电荷q,
已知球壳电势为Ua,则壳内任一点P
的电势为
对不对?
【解】
根据电势叠加原理
q
Q
R
P
r
P点的电势为
q
Q
R
P
r
球壳的电势为
为什么不对?
原来Ua并不是Q单独存在时的电势。
电势叠加:
(结果一样)
方法二:
方法三:
结论是
(结果相同)
11.今有两个电容值均为C的电容器,其带
电量分别为Q和2Q,求两电容器在并联前
后总能量的变化?
C
C
+Q
+2Q
-2Q
-Q
前
C
+3Q
-3Q
C
后
【解】
并联前
并联后
电容为2C,
带电量为3Q
C
+Q
-Q
C
+2Q
-2Q
后
为什么能量减少了?能量到哪里去了?
问题是:并联以后两个电容器上的
电量还是原来的分布吗?
设
C
+q1
-q1
C
+q2
-q2
C
+q1
-q1
C
+q2
-q2
求 q1,q2:
由(2)得
由(1)得
C
+1.5Q
-1.5Q
C
+1.5Q
-1.5Q
原来是在电量的流动
过程中,电场的能量
损失掉了一些。
R
铜球
?r
13.黄铜球浮在相对介电常数为? r=3.0 的
大油槽中,球的一半浸在油中,球的
上半部在空气中,如图所示。
已知球上净电荷为 Q =2.0?10-6C,
(1)求球的上、下部分各有多少自由电荷?
(2)求下半球表面附近极化电荷的?’、q’?
R
铜球
?r
因为铜球是等势体,所以可以看成是空气
中的半球电容器和油为介质的半球电容器
并联:
(1)求球的上、下
部分各有多少
自由电荷?
【解】
……
(2)
……
(1)
得
可以解得
(2)求下半球表面附近极化电荷的?’、q’?
?r
R
铜球
S
作半球形高斯面 S 如图:
高斯定理
此 ?’、q’ 即为所求。
就有
可知
R
Q上
Q下
+q’
讨论:
即把极化电荷也算上,
球的上、下部分带电
情况是相同的。
对比
上半空间电场的分布可等效为均匀带电2Q上
的整个球面在空气中的电场分布,
R
铜球
?r
Q上
Q下 +q’= Q上
上半球的电势为
下半空间电场的分布可等效为均匀带电2Q下
的整个球面浸在油中的电场分布,即
由下半球的电势分布公式,还可以看出:
下半球的电势是一样的:
有
3.(P67/1)一绝缘导体球不带电,距球心 r 处放一点电荷+q,
金属球半径R,
求:(1)金属球上感应电荷在球心处产生的电场强度
及此时导体球的电势。
(2) 若将金属球接地,球上的净电荷为何?
导体为等势体,能求得球心o处的电势即可。
o
导体上感应电荷都在球表面,距球心R
电荷守恒
解:(1) 如图,
-
-
-
-
+
+
+
+
+q
接地 即
设:感应电量为
o点的电势为0 则
-
-
-
-
o
+q
(2) 若将金属球接地,球上的净电荷为何?
4(P67/3).带电q、半径为R1的导体球,其外同心放置一导体球壳,
壳内、外半径为R2、R3。
问:1)外球壳的电荷和电势;
2)外球壳接地后重新绝缘,外球壳的电荷和电势;
3)然后内球壳接地,内球的电荷及外球壳的电势。
解(1)无限远处电势为零
高斯定理和电量守恒
等效:三个均匀带电的球面
利用叠加原理
等势体
(2)外球壳接地,球壳外电场为零,q电荷流入大地
球壳内表面带电 -q,外表面:0。
接地后重新绝缘,由高斯定理和电量守恒得:
内表面电荷-q ,外表面:0
等效:两个均匀带电的球面
利用叠加原理
(3)内导体球接地,剩余电荷q′。
外球壳电势
则,壳内表面:-q′
外表面:-q+q′
内球壳电势
6(P72/2).一球形电容器内、外导体球壳A和B的半径R1和R2,
两球壳间充满两层球壳形的均匀各向同性介质?r1、 ?r2,两介质分层处半径R,内球壳带电Q。
求:(1)两介质区的
(2)介质区的电能密度?
(3) 四个界面上的束缚面电荷密度?=?
R2
R
R1
?r2
?r1
A
B
Q
(1)介质区:
R2
R
R1
?r2
?r1
A
B
Q
(2)
(3)
介质
内表面
外表面
介质
内表面
外表面
