2020—2021学年人教A版高二数学《两直线的夹角》课件(21张PPT)
文档属性
| 名称 | 2020—2021学年人教A版高二数学《两直线的夹角》课件(21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 799.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-14 21:21:37 | ||
图片预览






文档简介
两直线的夹角
复习巩固
平面内两直线的位置关系有哪些?
相交、平行、重合
两相交直线可以用什么量来刻画它们的相交程度?
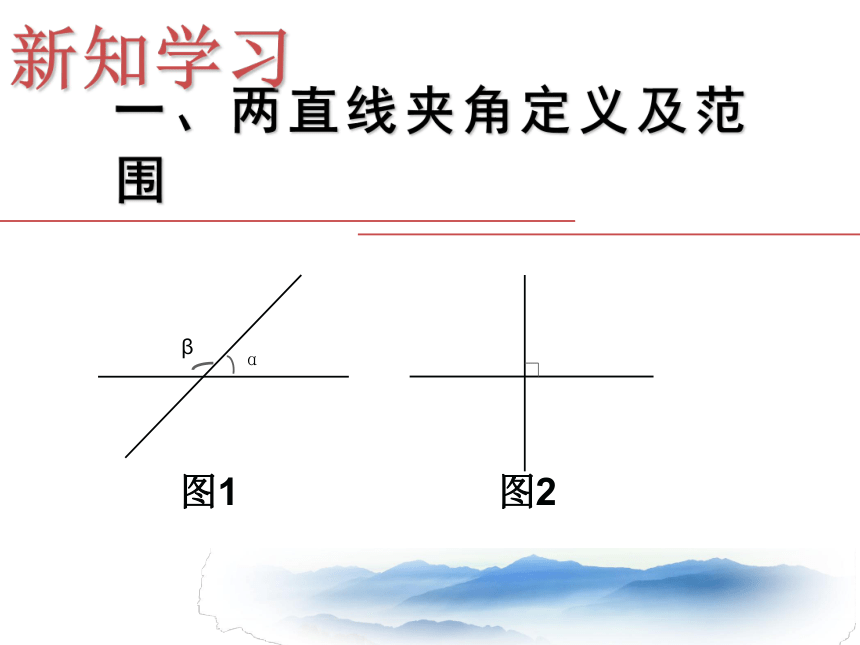
一、两直线夹角定义及范围
新知学习
α
β
图1
图2
1.两条相交直线的夹角:
两条相交直线所成的锐角或直角.
2.如果两条直线平行或重合,我们
规定它们的夹角为
3.平面上两条直线夹角的范围:
0
二、两直线夹角公式的探究
已知两条直线:
求两直线夹角 的大小.
已知两直线方程求夹角
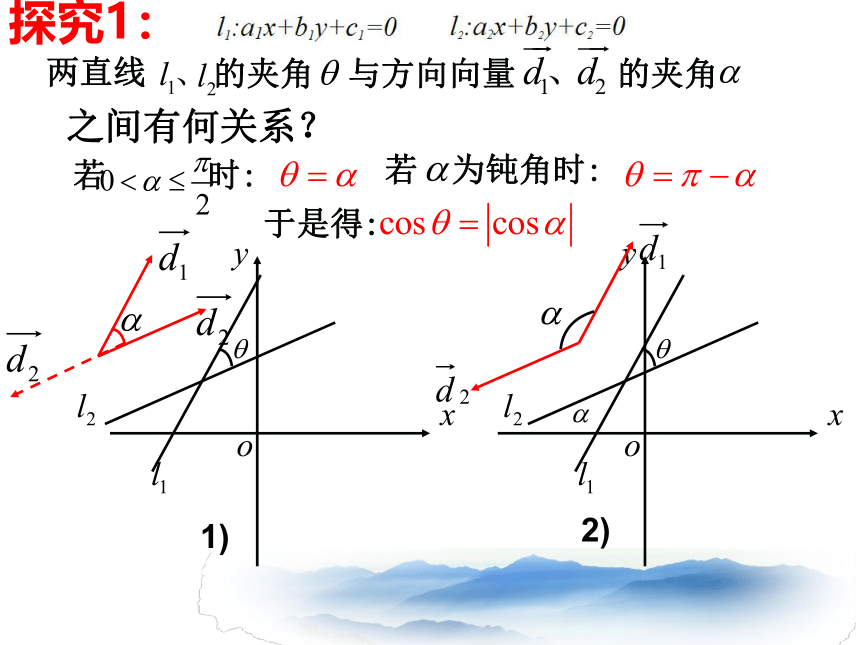
于是得:
1)
若 时:
若 为钝角时:
两直线
的夹角 与方向向量 的夹角
之间有何关系?
探究1:
2)
解:根据 与 的方程,取
为 与 的方向向量.
由向量的夹角公式得:
所以两直线的夹角公式:
向量推导
由
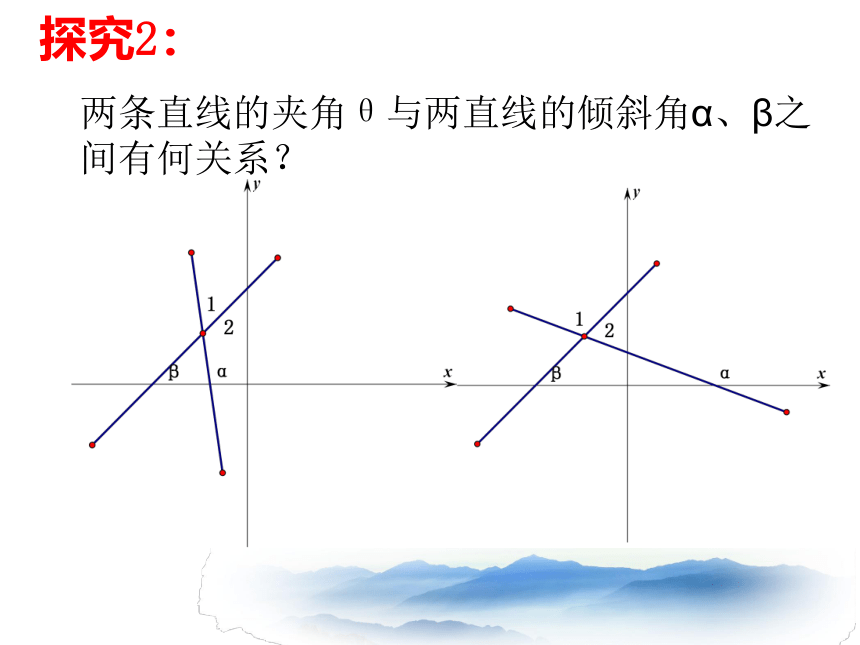
探究2:
两条直线的夹角θ与两直线的倾斜角α、β之间有何关系?
三、典型例题讲练
解:(1)根据 与 的方程及两直线夹角公式可得:
即直线 和 的夹角为
因为 ,所以
例1.求直线 的夹角 :
练习:求下列各组直线的夹角:
解:(1)根据 与 的方程及两直线夹角公式可得:
即直线 和 的夹角为
因为 ,所以
练习:求下列各组直线的夹角:
根据 与 的方程及两直线夹角公式可得:
即直线 和 的夹角为
因为 ,所以
例2.已知直线l 经过点P(-2,1),且与直线l0:3x-4y+5=0
的夹角为 ,求直线l 的方程。
1)当直线斜率存在时,设直线方程为y-1=k(x+2),
即kx-y+2k+1=0;
解:
所以有
解得
所以直线方程为7x+24y-10=0;
因为两直线夹角为 ,
o
x
y
例2.已知直线l 经过点P(-2,1),且与直线l0:3x-4y+5=0
的夹角为 ,求直线l 的方程。
2)直线斜率不存在时,
l:x+2=0;
经验证可知也满足题意;
由1)、2)可知,方程为7x+24y-10=0 或x=2;
解:
法二:设直线l 的一个法向量为 (a,b不全为0),则直线的点法向式方程为
整理得:
当b=0时直线l 的方程为x+2=0;
当 时直线l 的方程为7x+24y-10=0;
所以直线l 的方程为x+2=0或7x+24y-10=0;
整理得:
即:b(24a-7b)=0,
因为l与l0的夹角为 ,由两直线夹角公式得:
例2.已知直线l 经过点P(-2,1),且与直线l0:3x-4y+5=0
的夹角为 ,求直线l 的方程。
练习1
1.已知直线l经过原点,且与直线
的夹角为 ,求直线l的方程;
若直线l与直线2x-3y+6=0交于y轴,且它们的夹角为45o,求直线l的方程;
练习2
1、本节课通过两直线方程利用直线的方向向量所成的角与两直线夹角的关系定量的探究了两条直线的夹角,推导出两条直线的夹角公式;
2、熟练运用夹角公式求两条直线的夹角,注意不垂直的两条相交直线的夹角为锐角;
3、进一步讨论了求直线方程的方法:运用待定系数法时,可设直线方程为点法向式、或点斜式方程,而在用点斜式方程时,需要分类讨论.
课堂总结
作业:
课时练P25 课后巩固
再见
感谢各位老师莅临指导!
复习巩固
平面内两直线的位置关系有哪些?
相交、平行、重合
两相交直线可以用什么量来刻画它们的相交程度?
一、两直线夹角定义及范围
新知学习
α
β
图1
图2
1.两条相交直线的夹角:
两条相交直线所成的锐角或直角.
2.如果两条直线平行或重合,我们
规定它们的夹角为
3.平面上两条直线夹角的范围:
0
二、两直线夹角公式的探究
已知两条直线:
求两直线夹角 的大小.
已知两直线方程求夹角
于是得:
1)
若 时:
若 为钝角时:
两直线
的夹角 与方向向量 的夹角
之间有何关系?
探究1:
2)
解:根据 与 的方程,取
为 与 的方向向量.
由向量的夹角公式得:
所以两直线的夹角公式:
向量推导
由
探究2:
两条直线的夹角θ与两直线的倾斜角α、β之间有何关系?
三、典型例题讲练
解:(1)根据 与 的方程及两直线夹角公式可得:
即直线 和 的夹角为
因为 ,所以
例1.求直线 的夹角 :
练习:求下列各组直线的夹角:
解:(1)根据 与 的方程及两直线夹角公式可得:
即直线 和 的夹角为
因为 ,所以
练习:求下列各组直线的夹角:
根据 与 的方程及两直线夹角公式可得:
即直线 和 的夹角为
因为 ,所以
例2.已知直线l 经过点P(-2,1),且与直线l0:3x-4y+5=0
的夹角为 ,求直线l 的方程。
1)当直线斜率存在时,设直线方程为y-1=k(x+2),
即kx-y+2k+1=0;
解:
所以有
解得
所以直线方程为7x+24y-10=0;
因为两直线夹角为 ,
o
x
y
例2.已知直线l 经过点P(-2,1),且与直线l0:3x-4y+5=0
的夹角为 ,求直线l 的方程。
2)直线斜率不存在时,
l:x+2=0;
经验证可知也满足题意;
由1)、2)可知,方程为7x+24y-10=0 或x=2;
解:
法二:设直线l 的一个法向量为 (a,b不全为0),则直线的点法向式方程为
整理得:
当b=0时直线l 的方程为x+2=0;
当 时直线l 的方程为7x+24y-10=0;
所以直线l 的方程为x+2=0或7x+24y-10=0;
整理得:
即:b(24a-7b)=0,
因为l与l0的夹角为 ,由两直线夹角公式得:
例2.已知直线l 经过点P(-2,1),且与直线l0:3x-4y+5=0
的夹角为 ,求直线l 的方程。
练习1
1.已知直线l经过原点,且与直线
的夹角为 ,求直线l的方程;
若直线l与直线2x-3y+6=0交于y轴,且它们的夹角为45o,求直线l的方程;
练习2
1、本节课通过两直线方程利用直线的方向向量所成的角与两直线夹角的关系定量的探究了两条直线的夹角,推导出两条直线的夹角公式;
2、熟练运用夹角公式求两条直线的夹角,注意不垂直的两条相交直线的夹角为锐角;
3、进一步讨论了求直线方程的方法:运用待定系数法时,可设直线方程为点法向式、或点斜式方程,而在用点斜式方程时,需要分类讨论.
课堂总结
作业:
课时练P25 课后巩固
再见
感谢各位老师莅临指导!
