2020—2021学年人教A版高二数学《双曲线的标准方程教学》课件(27张PPT)
文档属性
| 名称 | 2020—2021学年人教A版高二数学《双曲线的标准方程教学》课件(27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 715.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-14 00:00:00 | ||
图片预览







文档简介
生活中有双曲线,生活中用双曲线
2.6.1双曲线的标准方程
1.结合实际情景熟悉双曲线的定义、几何图形和标准方程的推导过程(逻辑推理、数学抽象)
2.掌握双曲线的标准方程及其求法。(数学运算)
3.与椭圆的标准方程进行比较,并加以区分。(逻辑推理)
对标导学
核心素养
1.双曲线的定义
思考1:结合课本双曲线拉链实验,归纳双曲线的定义包含几个要素?
(1)已知 F1,F2 是平面内两个定点,a是一个正常数,且2a< |F1,F2| ,则平面上满足___________________的动点M的轨迹称为双曲线,其中,两个定点________称为双曲线的焦点,两个焦点的距离_______称为双曲线的焦距。
(2)在双曲线的定义中要注意条件“0<2a< |F1,F2| ”;
2.双曲线的标准方程及其推导
(1)推导双曲线的标准方程,要分几步?采用什么方法化简方程?
(2)当双曲线的焦点在x轴上时,双曲线的标准方程是_____。
当双曲线的焦点在y轴上时,双曲线的标准方程是_____。
(3)标准方程中的两个参数a,b和半焦距c的关系是_____。
(4)怎么判断双曲线的焦点在哪个轴上?
自学静悟
1.双曲线的定义
思考1:结合课本双曲线拉链实验,归纳双曲线的定义包含几个要素?
(1)已知 F1,F2 是平面内两个定点,a是一个正常数,且2a< |F1,F2| ,则平面上满足___________________的动点M的轨迹称为双曲线,其中,两个定点________称为双曲线的焦点,两个焦点的距离_______称为双曲线的焦距。
(2)在双曲线的定义中要注意条件“0<2a< |F1,F2| ”;
2.双曲线的标准方程及其推导
(1)推导双曲线的标准方程,要分几步?采用什么方法化简方程?
(2)当双曲线的焦点在x轴上时,双曲线的标准方程是_____。
当双曲线的焦点在y轴上时,双曲线的标准方程是_____。
(3)标准方程中的两个参数a,b和半焦距c的关系是_____。
(4)怎么判断双曲线的焦点在哪个轴上?
合作学习
回顾
展示分享
1.双曲线的定义
椭圆的定义: 平面上到两个定点的距离之和等于定长的点的集合叫椭圆.
思考2:如果把椭圆定义中的“距离之和”改为“距离
之差”,那么动点的轨迹会是怎样的曲线?
椭圆的标准方程:
a2=b2+c2
数学实验
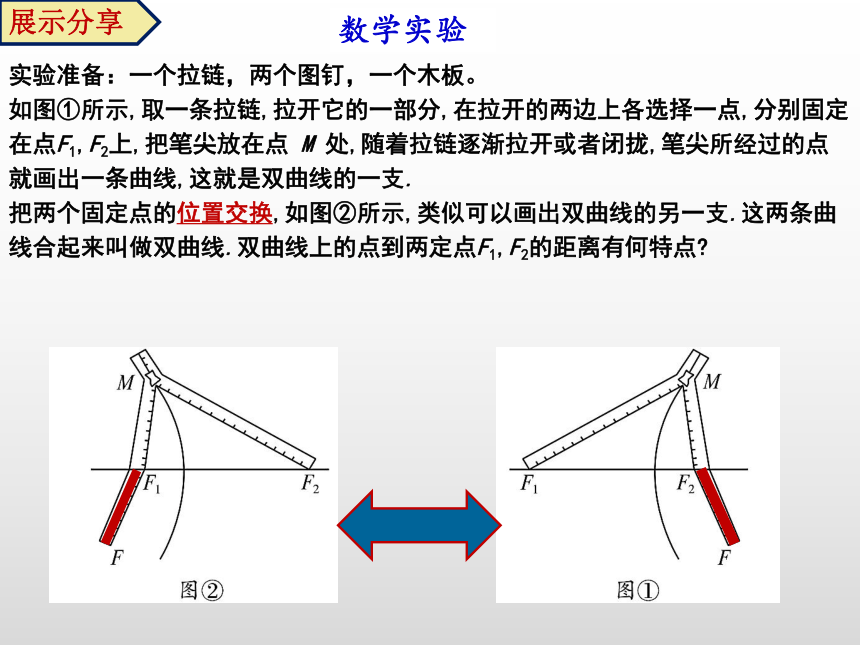
实验准备:一个拉链,两个图钉,一个木板。
如图①所示,取一条拉链,拉开它的一部分,在拉开的两边上各选择一点,分别固定在点F1,F2上,把笔尖放在点 M 处,随着拉链逐渐拉开或者闭拢,笔尖所经过的点就画出一条曲线,这就是双曲线的一支.
把两个固定点的位置交换,如图②所示,类似可以画出双曲线的另一支.这两条曲线合起来叫做双曲线.双曲线上的点到两定点F1,F2的距离有何特点?
展示分享
用拉链绘制双曲线动画演示
请你归纳出双曲线的定义,它应该包含几个要素?
请你归纳出双曲线的定义,它应该包含几个要素?
(1)由于图钉固定,拉链长度固定,这里截取
由此可知
(2)点M到两个定点的距离之差的绝对值要小于两个定点之间的距离。
即
| |MF1|-|MF2| | = 2a
(差的绝对值)
1.双曲线的定义
双曲线定义的文字表述:
平面内到两个定点F1,F2的距离之差的绝对值等于常数 (2a )(2a<|F1F2 |)的点的轨迹叫双曲线。
定点F1、F2叫做双曲线的焦点
两焦点之间的距离叫做双曲线的焦距(2c)
双曲线定义的符号表述:
展示分享
探讨:当2a>2c时,M的轨迹?
当2a=2c时,M的轨迹?
图像特征???
1、建系设点
2、列式
3、代数方程
4、化简方程
2.双曲线标准方程的推导
①
(-c,0)
(c,0)
(x,y)
展示分享
②
①
分子有理化去掉根号
它所表示的双曲线的焦点在x轴上,焦点坐标是
其中
2.双曲线的标准方程的推导
展示分享
刚才我们得到了焦点在x轴上的双曲线方程,
如何推导焦点在y轴上的双曲线的标准方程呢?
展示分享
焦点位置
焦点在x轴上
焦点在y轴上
图形
标准方程
(a>0,b>0)
(a>0,b>0)
焦点
F1(-c,0),F2(c,0)
F1(0,-c),F2(0,c)
a,b,c的关系
b2=c2-a2
双曲线的标准方程两种形式
思考3:类比椭圆,如何根据双曲线的标准方程判断其焦
点在哪个坐标轴上?
展示分享
Y
对双曲线的标准方程的再认识
(1)双曲线标准方程的形式:左边是两个分式的平方差,右边是1。
(2)双曲线的标准方程中三个参数a、b、c满足c2=a2+b2。
(3)由双曲线的标准方程可以求出三个参数a、b、c的值。反之求出a.b.c 的值可写出双曲线的标准方程。
(4)双曲线的标准方程中,看x2,y2项的系数,哪个是正的,焦点就在哪个轴上。
(a>0,b>0)
(a>0,b>0)
口诀:焦点跟着正项走!!!
展示分享
则a= ,b= ;
,则a= ,b= ;
4
3
3
2
快速反应
焦点坐标为:___________
焦距等于__10_;
焦点坐标为:___________
焦距等于______
根据双曲线的标准方程求参数a,b,c的值。
展示分享
例题1:求适合下列条件的双曲线的标准方程。
双曲线的一个焦点坐标是(0,-6),且双曲线经过点A(-5,6)。
3.应用举例
解:因为双曲线的焦点在y轴上,所以设它的标准方程为
定义法
展示分享
(a>0,b>0)
因为点A在双曲线上,所以点A与两交点的距离的差的绝对值为
变式训练1 :求适合下列条件的双曲线的标准方程。
两个焦点的坐标分别是(-5,0) ,(5,0),且双曲线上的点与两焦点距离之差的绝对值等于8。
解:因为双曲线的焦点在x轴上,所以设它的标准方程为
(a>0,b>0)
待定系数法
展示分享
例题2:求下列方程表示的双曲线的焦点坐标
展示分享
变式训练2:求下列方程表示的双曲线的焦点坐标
展示分享
1.根据下列条件,求双曲线的标准方程。
(1) , 焦点在y轴上;
(2) ,经过点(-4,0),焦点在x轴上;
2.已知方程 表示焦点在y轴上的双曲线,则m的取
值范围是多少?
达标检测
这节课你收获了什么?
1.双曲线的定义,双曲线图像有两支,且是不封闭的
2.双曲线标准方程的推导中,使用了分子有理化
3.双曲线中a,b,c三者之间的关系
4.根据双曲线的标准方程判断焦点在哪个坐标轴上
点评精讲
小结 ----双曲线定义及标准方程
定义
图象
方程
焦点
a.b.c 的关系
| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)
F ( ±c, 0) F(0, ± c)
完成《同步练习册》与《分层训练》相应章节!!
课后练习
?
思考:双曲线的标准方程与椭圆的标准方程有何区别与联系?
2.6.1双曲线的标准方程
1.结合实际情景熟悉双曲线的定义、几何图形和标准方程的推导过程(逻辑推理、数学抽象)
2.掌握双曲线的标准方程及其求法。(数学运算)
3.与椭圆的标准方程进行比较,并加以区分。(逻辑推理)
对标导学
核心素养
1.双曲线的定义
思考1:结合课本双曲线拉链实验,归纳双曲线的定义包含几个要素?
(1)已知 F1,F2 是平面内两个定点,a是一个正常数,且2a< |F1,F2| ,则平面上满足___________________的动点M的轨迹称为双曲线,其中,两个定点________称为双曲线的焦点,两个焦点的距离_______称为双曲线的焦距。
(2)在双曲线的定义中要注意条件“0<2a< |F1,F2| ”;
2.双曲线的标准方程及其推导
(1)推导双曲线的标准方程,要分几步?采用什么方法化简方程?
(2)当双曲线的焦点在x轴上时,双曲线的标准方程是_____。
当双曲线的焦点在y轴上时,双曲线的标准方程是_____。
(3)标准方程中的两个参数a,b和半焦距c的关系是_____。
(4)怎么判断双曲线的焦点在哪个轴上?
自学静悟
1.双曲线的定义
思考1:结合课本双曲线拉链实验,归纳双曲线的定义包含几个要素?
(1)已知 F1,F2 是平面内两个定点,a是一个正常数,且2a< |F1,F2| ,则平面上满足___________________的动点M的轨迹称为双曲线,其中,两个定点________称为双曲线的焦点,两个焦点的距离_______称为双曲线的焦距。
(2)在双曲线的定义中要注意条件“0<2a< |F1,F2| ”;
2.双曲线的标准方程及其推导
(1)推导双曲线的标准方程,要分几步?采用什么方法化简方程?
(2)当双曲线的焦点在x轴上时,双曲线的标准方程是_____。
当双曲线的焦点在y轴上时,双曲线的标准方程是_____。
(3)标准方程中的两个参数a,b和半焦距c的关系是_____。
(4)怎么判断双曲线的焦点在哪个轴上?
合作学习
回顾
展示分享
1.双曲线的定义
椭圆的定义: 平面上到两个定点的距离之和等于定长的点的集合叫椭圆.
思考2:如果把椭圆定义中的“距离之和”改为“距离
之差”,那么动点的轨迹会是怎样的曲线?
椭圆的标准方程:
a2=b2+c2
数学实验
实验准备:一个拉链,两个图钉,一个木板。
如图①所示,取一条拉链,拉开它的一部分,在拉开的两边上各选择一点,分别固定在点F1,F2上,把笔尖放在点 M 处,随着拉链逐渐拉开或者闭拢,笔尖所经过的点就画出一条曲线,这就是双曲线的一支.
把两个固定点的位置交换,如图②所示,类似可以画出双曲线的另一支.这两条曲线合起来叫做双曲线.双曲线上的点到两定点F1,F2的距离有何特点?
展示分享
用拉链绘制双曲线动画演示
请你归纳出双曲线的定义,它应该包含几个要素?
请你归纳出双曲线的定义,它应该包含几个要素?
(1)由于图钉固定,拉链长度固定,这里截取
由此可知
(2)点M到两个定点的距离之差的绝对值要小于两个定点之间的距离。
即
| |MF1|-|MF2| | = 2a
(差的绝对值)
1.双曲线的定义
双曲线定义的文字表述:
平面内到两个定点F1,F2的距离之差的绝对值等于常数 (2a )(2a<|F1F2 |)的点的轨迹叫双曲线。
定点F1、F2叫做双曲线的焦点
两焦点之间的距离叫做双曲线的焦距(2c)
双曲线定义的符号表述:
展示分享
探讨:当2a>2c时,M的轨迹?
当2a=2c时,M的轨迹?
图像特征???
1、建系设点
2、列式
3、代数方程
4、化简方程
2.双曲线标准方程的推导
①
(-c,0)
(c,0)
(x,y)
展示分享
②
①
分子有理化去掉根号
它所表示的双曲线的焦点在x轴上,焦点坐标是
其中
2.双曲线的标准方程的推导
展示分享
刚才我们得到了焦点在x轴上的双曲线方程,
如何推导焦点在y轴上的双曲线的标准方程呢?
展示分享
焦点位置
焦点在x轴上
焦点在y轴上
图形
标准方程
(a>0,b>0)
(a>0,b>0)
焦点
F1(-c,0),F2(c,0)
F1(0,-c),F2(0,c)
a,b,c的关系
b2=c2-a2
双曲线的标准方程两种形式
思考3:类比椭圆,如何根据双曲线的标准方程判断其焦
点在哪个坐标轴上?
展示分享
Y
对双曲线的标准方程的再认识
(1)双曲线标准方程的形式:左边是两个分式的平方差,右边是1。
(2)双曲线的标准方程中三个参数a、b、c满足c2=a2+b2。
(3)由双曲线的标准方程可以求出三个参数a、b、c的值。反之求出a.b.c 的值可写出双曲线的标准方程。
(4)双曲线的标准方程中,看x2,y2项的系数,哪个是正的,焦点就在哪个轴上。
(a>0,b>0)
(a>0,b>0)
口诀:焦点跟着正项走!!!
展示分享
则a= ,b= ;
,则a= ,b= ;
4
3
3
2
快速反应
焦点坐标为:___________
焦距等于__10_;
焦点坐标为:___________
焦距等于______
根据双曲线的标准方程求参数a,b,c的值。
展示分享
例题1:求适合下列条件的双曲线的标准方程。
双曲线的一个焦点坐标是(0,-6),且双曲线经过点A(-5,6)。
3.应用举例
解:因为双曲线的焦点在y轴上,所以设它的标准方程为
定义法
展示分享
(a>0,b>0)
因为点A在双曲线上,所以点A与两交点的距离的差的绝对值为
变式训练1 :求适合下列条件的双曲线的标准方程。
两个焦点的坐标分别是(-5,0) ,(5,0),且双曲线上的点与两焦点距离之差的绝对值等于8。
解:因为双曲线的焦点在x轴上,所以设它的标准方程为
(a>0,b>0)
待定系数法
展示分享
例题2:求下列方程表示的双曲线的焦点坐标
展示分享
变式训练2:求下列方程表示的双曲线的焦点坐标
展示分享
1.根据下列条件,求双曲线的标准方程。
(1) , 焦点在y轴上;
(2) ,经过点(-4,0),焦点在x轴上;
2.已知方程 表示焦点在y轴上的双曲线,则m的取
值范围是多少?
达标检测
这节课你收获了什么?
1.双曲线的定义,双曲线图像有两支,且是不封闭的
2.双曲线标准方程的推导中,使用了分子有理化
3.双曲线中a,b,c三者之间的关系
4.根据双曲线的标准方程判断焦点在哪个坐标轴上
点评精讲
小结 ----双曲线定义及标准方程
定义
图象
方程
焦点
a.b.c 的关系
| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)
F ( ±c, 0) F(0, ± c)
完成《同步练习册》与《分层训练》相应章节!!
课后练习
?
思考:双曲线的标准方程与椭圆的标准方程有何区别与联系?
